Bézier-Said-Wang型广义Ball曲线的细分算法

王 燕，李志明

(1.合肥师范学院 数学与统计学院,安徽 合肥 230601；2. 合肥工业大学 计算机与信息学院，安徽 合肥 230009)



Bézier-Said-Wang型广义Ball曲线的细分算法

王 燕1，李志明2

(1.合肥师范学院 数学与统计学院,安徽 合肥 230601；2. 合肥工业大学 计算机与信息学院，安徽 合肥 230009)

利用BSWGB曲线的对偶基给出了BSWGB曲线的显式细分算法。与传统的细分方法相比，该算法避免了繁琐的矩阵求逆运算和基转换运算，而且该算法的使用可归结为细分矩阵与顶点向量阵的乘积，易于绘图。该方法给出了现有的一些广义Ball曲线的细分矩阵的统一表达式，可以很方便的利用此表达式，解决这一类曲线的细分问题。最后通过实例证明了本文算法的有效性。

BSWGB曲线；对偶基；细分算法；细分矩阵

用于CONSURF系统的三次Ball曲线是Ball在1974年提出的[1]。从此之后，许多学者对三次Ball曲线作了扩展[2-7]。随着Said-Ball曲线、Wang-Ball 曲线等广义Ball曲线的提出，许多学者开始研究各种不同的广义Ball曲线的统一表示。Wu[8]提出了Wang-Said型广义Ball曲线和Said- Bézier型广义Ball曲线(分别简称为WSGB曲线和SBGB曲线)，分别得到了 Wang-Ball 曲线和Said-Ball曲线，以及Said-Ball曲线和 Bézier曲线的统一表示。沈[9]构造了一组介于Wang-Ball 曲线和Said-Ball曲线之间的新的广义Ball曲线。汪志华和朱晓临[10]给出了Bézier曲线和Wang-Ball 曲线的统一表示，简称WBGB曲线。张莉[11]提出了Bézier-Said-Wang型广义Ball曲线，包含了现有的广义Ball曲线(Said- Ball 曲线、Wang-Ball曲线、WSGB曲线、SBGB曲线和WBGB曲线)，Bézier曲线以及中间曲线。

细分算法是CAGD中构造曲线曲面的一种有效的方法，在曲线曲面的降阶、求交等中具有重要的作用。王国瑾[4]中给出了Wang-Ball曲线的细分方法：首先求出Wang-Ball基转换成幂基的转换矩阵，然后求转换矩阵的逆矩阵，再乘以另一个由转换矩阵演化得到的矩阵。该方法适用于任何多项式参数曲线, 是一种普遍适用的方法，但未给出显式表达式。蒋素荣和王国瑾[12]运用类似的方法给出了Wang-Ball曲线的中点离散公式。余等[13]给出了Wang-Ball曲线的细分算法。2006年，江和檀[14]给出了WSGB曲线的细分算法。本文利用文献[11]中提出的对偶基给出了BSWGB曲线的细分算法。这个方法与传统的细分方法相比，可以避免繁琐的矩阵求逆运算和BSWGB基转换成幂基的运算。并且，当BSWGB基中的参数K和L取不同的值时，该方法给出了现有的一些广义Ball曲线的细分算法的统一表示。

1 Bézier-Said-Wang型广义Ball曲线

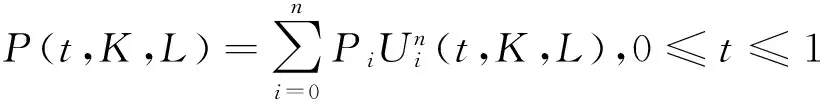
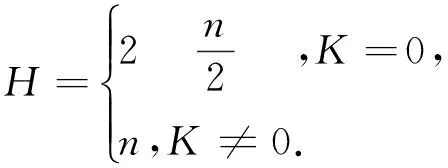
2 BSWGB基函数的对偶基

(1)

(2)

其中,

(i,j=0,1,…,n).

3 BSWGB曲线的细分算法

不失一般性，我们假设n=2m+1。

给定一个实数c,0≤c≤1，记

(3)

和

(4)

分别表示BSWGB曲线在区间[0,c]和[c,1]上相应的部分。

(5)

(6)

定理2 由式(5)定义的曲线的控制顶点定义如下：

(Q0,Q1,…,Qn)T=S(c)(P0,P1,…,Pn)T,

(7)

其中S(c)=(sij)(2m+2)×(2m+2)称为细分矩阵，矩阵的元素为：

1) 0≤i≤m-K-L,

(8)

(9)

(10)

(11)

2)m-K-L+1≤i≤m-L,

(12)

(13)

(14)

(15)

3)m-L+1≤i≤m

(16)

(17)

(18)

(19)

证明 由定理1，公式(3)，公式(5)和公式(7) 可以得到：

sij=λiUj(ct,K,L),s2m+1-i,j=λ2m+1-iUj(ct,K,L),

第一种情况。当0≤i≤m-K-L，

(1)当0≤j≤m-K-L时，

(2)当m-K-L+1≤j≤m-L-1时，

(3)当m-L≤j≤m-1时，

(4)当j=m时，

由(1) ～ (4)，可以证明公式(8) 和公式(9)。

同理可以由公式(2)证明公式(10)和(11) 。

第2种情况。当m-K-L+1≤i≤m-L时，证明过程完全类似于第1种情况。由公式(1)和公式(2)，可以得到公式(12) ～ 公式 (15)。

第3种情况。当m-L+1≤i≤m时，由公式(1)可以得到

当0≤j≤m-K-L时，

当m-K-L+1≤j≤m-L-1，m-L≤j≤m-1和j=m 时，可以得到类似的结果，即公式(16) 和公式(17) 。

同理可以由公式(2)得到公式(10) 和公式(11) 。

证毕。

根据BSWGB基函数的对称性和定理2，得到下面的定理3。

定理3 由式(6)定义的曲线的控制顶点为：

4 数值例子

例1 令n=5,K=L=1，由定理2可以得到如下细分矩阵：

例2 令n=7,K=0,L=1时，BSWGB曲线即为WSGB曲线，可以得到与文献[15]中一样的细分矩阵：

曲线曲面的细分算法用于曲线曲面的降阶，可以提高降阶的精度，降低降阶的误差，下面举例说明。

例3 文献[16]中给出了n=7,L=1时的WSGB曲线(对应本文的n=7,K=0,L=1的BSWGB曲线)的降阶，原曲线的控制顶点为{(220,110),(160,220),(180,340),(260,400),

(355,425),(470,320),(490,200),(420,100)},利用扰动法将一阶后的曲线的控制顶点为{(220,110),(160,220),(180,340),(307.5,412.5),(470,320),(490,200),(420,100)}(如图1)，降阶误差为error=17.813，降阶误差比较大，这时候可以利用WSGB曲线的细分算法对曲线做细分，再逐段用扰动法降阶。

图1 七次WSGB曲线的降阶

由例2得到的细分矩阵将该WSGB曲线细分一次(取c=0.5)，所得的细分曲线如图2(a)所示，然后用扰动法分别对两段曲线进行降阶，得到的降阶曲线如图2(b)所示。

图2 七次WSGB曲线细分后降阶

为了更好的理解，给出了降阶前后控制多边形和曲线的局部放大图(如图2(c)-2(f)所示)。细分后再利用扰动法降阶的误差为error=0.0366，比直接利用扰动法降阶的误差大大的减少了。

5 结论

本文给出了BSWGB曲线的显式细分算法，包含Said-Ball曲线、Wang-Ball曲线、 WSGB曲线、SBGB曲线、WBGB曲线和中间曲线的细分矩阵。可以利用这个细分矩阵解决这类曲线的细分问题，只需要修改参数K和L,就可以快速的得到中间状态的其它过渡曲线的细分矩阵, 加快了曲线、曲面的生成速度, 对计算机辅助几何设计及图形绘制系统的效率具有重要的意义。最后用实例说明了本文方法的有效性，并举例说明了细分算法在曲线降阶中的应用，细分后再进行降阶比直接降阶所得的误差要小。本文的方法也可推广到曲面细分的情形。

[1] A.A. Ball, CONSURF. Part one: Introduction of the conic lofting tile [J]. Computer-Aided Design, 1974, 6 (4): 243-249.

[2] A.A. Ball, CONSURF. Part two: Description of the algorithms [J]. Computer-Aided Design, 1975, 7 (4): 237-242.

[3] H.B. Said. A generalized Ball curve and its recursive algorithm [J]. ACM Transactions on Graphics, 1989, 8 (4): 360-371.

[4]王国瑾. 高次Ball曲线及其几何性质[J]. 高校应用数学学报(A辑),1987, 2(1): 126-140.

[5] T.N.T. Goodman, H.B. Said. Properties of generalized Ball curves and surfaces [J]. Computer-Aided Design, 1991, 23 (8): 554-560.

[6] T.N.T. Goodman, H.B. Said. Shape-preserving properties of the generalized Ball basis [J]. Computer Aided Geometric Design, 1991, 8 (2): 115-121.

[7] S.M. Hu, G.Z. Wang, T.G. Jin. Properties of two types of generalized Ball curves [J]. Computer-Aided Design, 1996, 28 (2): 125-133.

[8] H.Y. Wu. Unifying representation of Bézier curve and generalized Ball curves [J]. Applied Mathematics: A Journal of Chinese Universities Series B, 2000, 15 (1): 109-121.

[9]沈莞蔷, 汪国昭. Ball基的推广[J]. 软件学报, 2005, 16 (11): 1992-1999.

[10]汪志华, 朱晓临. Bézier曲线与Wang-Ball曲线的统一表示[J]. 计算机辅助设计与图形学学报, 2008, 20 (7): 888-893.

[11] L. Zhang, J.Q. Tan, Z.Y. Dong. The dual bases for the Bézier-Said-Wang type generalized Ball polynomial bases and their applications [J]. Applied Mathematics and Computations, 2010, 217 (7): 3088-3101.

[12] 蒋素荣, 王国瑾. Bézier 曲线到Wang-Ball 曲线的转换矩阵及其应用[J]. 计算机学报, 2005, 28 (1): 75-80 .

[13] 余宏杰, 江平, 汪峻萍等. Wang-Ball 曲线的细分算法及包络[J]. 计算机辅助设计与图形学学报, 2005, 17 (4) : 637- 643.

[14] P. Jiang, J.Q. Tan. The subdivision algorithm for the generalized Ball curves [J]. Journal of Information & Computational Science, 2006, 3 (1): 21-31.

[15] 余宏杰. Wang-Said型广义Ball曲线的细分算法[J]. 计算机辅助设计与图形学学报, 2009, 21 (5) : 600-605.

[16] 江平, 檀结庆. Wang-Said型广义Ball曲线的降阶 [J]. 软件学报, 2006, 17(增刊): 93-102.

The Subdivision Algorithm for Bézier-Said-Wang Type Generalized Ball Curves

WANG Yan, LI Zhiming

(1. School of Mathematics and Statistics, Hefei Normal University, Hefei 230601;2. School of Computer and Information, Hefei University of Technology, Hefei 230009)

This method gives an explicit subdivision matrix by using the dual bases of BSWGB bases, which is different from with the traditional subdivision algorithm needed to convert BSWGB bases into power bases and solve the inverse matrix. The algorithm can be efficiently achieved by multiple of subdivision matrix and vector of the vertices which leads to simple drawing of the curves. This algorithm is the unifying representation of subdivision matrices of the existed generalized Ball curves, which can be used in solving the subdivision of this kind of curves. Numerical examples are also given to show the effectiveness of our methods.

BSWGB curves; dual basis; subdivision algorithm; subdivision matrix

2016-08-10

合肥师范学院人才科研启动基金(2014rcjj05)

王燕(1985-)，女，山东泰安人，讲师，博士，主要研究方向为：计算机辅助几何设计。

TP391.72

A

1674-2273(2016)06-0001-9