直埋供热管道直角弯管热-力耦合分析

江超,官燕玲,邓顺熙,孟庆龙,石娟玲,曹宏麟

(1.长安大学环境科学与工程学院,710054,西安;2.西安市热力总公司,710016,西安)



直埋供热管道直角弯管热-力耦合分析

江超1,官燕玲1,邓顺熙1,孟庆龙1,石娟玲2,曹宏麟2

(1.长安大学环境科学与工程学院,710054,西安;2.西安市热力总公司,710016,西安)

针对直埋热水供热管道弯管受力的复杂性,基于土弹簧模型建立了三维热-力耦合有限元模型,分析了直埋直角弯管应力的主要影响因素,给出了缩短弯臂长度的热-力耦合有限元模型。建模中管土相互作用考虑了介质的重力和覆土重力等的作用,弯头管段的边界条件施加在2个弯臂端头。结果表明,直埋弯管在温升作用下的峰值应力远大于内压作用下的峰值应力;直埋弯管的一次应力随管道壁厚、管道埋深的增加而降低,随内压、弯头曲率半径的增加而增加;直埋弯管的二次应力随管道壁厚的增加而降低,随内压、埋深、温升、弯头曲率半径、弯头端部位移的增加而增加;弯头截面竖向椭圆化对弯头是有利的,而横向椭圆化是有害的;地面荷载作用使弯头最大当量应力减小,对弯头起保护作用。该研究旨在为直埋管道的安全性分析提供帮助。

直埋供热管道;弯管;应力;热-力耦合分析;有限元模型

直埋供热管道在定线时因受到道路线形、邻近管线以及障碍物的影响,经常需要设计成弯曲管线。弯曲管线在受热情况下两臂产生位移,弯头处产生较大的横向变形。横向变形受到周围土壤的束缚又会产生土壤的侧反力,进而使得弯头的受力十分复杂。设计规程[1]指出,弯管可采用有限元法计算,但没有给出具体方法。

Peng建立的直埋弯头分析中将弯头简化为刚性联结点,并给出了90°埋地弯头解析计算公式[2]。崔孝秉提出了弹性抗弯铰解析计算公式,并给出了简化方法[3]。

近些年来,对弯头的研究多为非直埋弯头的有限元分析,主要采用ANSYS软件[4-9]。董俊华等采用ANSYS软件分析了不等壁厚弯头与等壁厚弯头的应力分布[4]。杜保存的模拟结果表明,弯头截面保持一定的椭圆度可以降低弯头危险区域的应力大小[5]。刘波采用ANSYS软件分析了圆形截面、椭圆截面和不均匀壁厚小管径弯头的应力分布[6]。以上研究表明,弯头椭圆化不会产生不利影响,但是由于没有考虑横向土压力与竖向土压力的区别,所以不能界定椭圆化位置的影响。

黄鉴等采用ANSYS软件分析了钢质弯头在不同内压下的应力特性[7]。张鹏等采用ANSYS软件分析了内压、轴向力和面弯矩联合作用下的弯头应力分布[8]。王国伟采用ANSYS模拟的方法,用COMBIN14弹簧-阻尼器单元来模拟土壤对管道的作用,对90°弯头进行了模拟分析[9]。

本文对DN 1 000 mm的大口径、1.0 MPa高压力的直埋供热管道弯头管段进行热-力耦合有限元应力分析。建模中,管土相互作用考虑了介质重力和覆土重力等的作用,弯头管段的边界条件施加在2个弯臂端头。

1 土弹簧模型

1.1 Winkler模型

土弹簧模型为Winkler模型[10-11],该模型为土的离散模型,土介质表面上任意一点的位移仅与作用在该点的应力成正比,而与作用在其他各点的应力无关,即

σ=kω

(1)

式中:σ为土介质表面某点处的应力;k为地基反力系数;ω为土介质表面某点处的位移。

1.2 土弹簧参数取值

如图1所示,直埋管道所受土弹簧作用可以分解为轴向弹簧kx、横向弹簧ky和竖向弹簧kz的作用[12]。所有弹簧均采用双线性模型进行分析,因此只需确定屈服力和屈服位移。

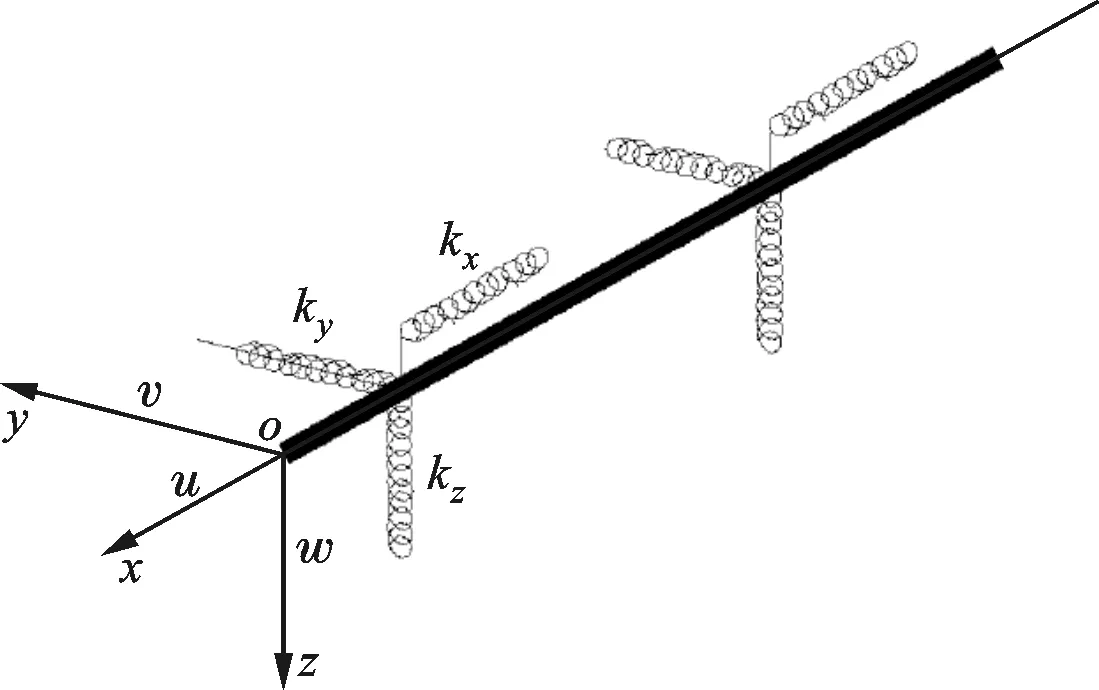
图1 管土作用三维土弹簧模型

轴向弹簧屈服力f取摩擦力,即土压力乘以摩擦系数[1],相应的屈服位移u取管外径的1%[13]。横向弹簧屈服力p取最大侧反力,即极限水平土压力[12],相应的屈服位移v取管中埋深的2%[12]。竖向弹簧屈服力q按文献[14]方法计算,相应的屈服位移w取管外径的2%[14]。

在DN 1 000 mm(管道的聚乙烯保护壳外径D′为1 155 mm)直埋热水管道的管顶覆土为1.4 m、土壤密度为1 800 kg/m3、内摩擦角为30°,黏聚力为12.5 kPa、管道与土壤之间的摩擦系数为0.4[1]时,若不考虑地下水浮力、地面交通荷载以及堆积荷载的作用,则双线性土弹簧的弹簧力(f、p、q)-位移(u、v、w)曲线见图2～图4。

2 管道模型

采用适用于薄壁及中等厚度壳体结构分析的Shell181单元对管道进行建模[15]。为详细得到弯头处的应力分布,对弯头区域附近的网格进行了加密,见图5。管道横截面布置4排弹簧,见图6:顶部弹簧为轴向土弹簧;左右两侧为横向土弹簧;底部为竖向土弹簧;弯头处仅布置外侧横向弹簧。考虑到弯头在2个方向受到土壤的横向作用,所以在这2个方向上分别施加横向土弹簧,见图7。弯头管段几何参数见表1,管道材料参数见表2。本文所选壁厚为理论壁厚,实际应用中应考虑壁厚偏差的影响。

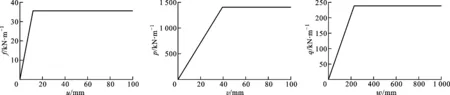
图2 轴向弹簧力-位移曲线 图3 横向弹簧力-位移曲线 图4 竖向弹簧力-位移曲线

表1 弯头管段几何参数

表2 管道材料参数[1]

(a)管内压力为1.0 MPa (b)图8a工况下按第2节设置土弹簧 (c)图8b工况下增加120 ℃温升荷载图8 弯头应力等值分布图

3 热-力耦合分析

本文将热膨胀与土壤压缩变形两者的耦合作用称为热-力耦合。直埋管道受热而不受周围土壤作用,管道中不存在轴向应力;管道受到周围土壤作用而无热作用,管道中的轴向应力可以忽略。热-力耦合作用下,管道中将产生很大的轴向应力,极易造成管道破坏。

3.1 热-力耦合计算

图8和图9给出了不同外荷载作用下弯头的应

力分布和位移分布。两图所计算的弯头臂长均为20 m,为清晰展现计算结果,仅给出了弯头附近的计算结果。在弯臂的端头设置了130 kN的轴力作用[16],以模拟补偿器的反力作用。

内压作用下,弯头的外拱处当量应力最低,为55.0 MPa(见图8a);增加土壤作用后,靠近弯头内拱处的弯臂上当量应力有所降低,为55.2 MPa(见图8b);增加温度荷载后,弯头顶部当量应力增加较多,为265 MPa,而内拱处当量应力下降,同时外拱处低应力区的范围有所减小(见图8c)。

无温升作用下,弯头的位移较小,为0.479 mm(图9a、9b),管土作用不明显,当量应力也较小;温升作用下,弯头内拱及弯头顶部产生了较大的位移,为34.788 mm,管土作用加强,从而产生了较大的当量应力(图9c)。

内压工况下环向应力分布见图10,弯头内拱、外拱和顶部的环向应力分别为63.7 MPa、42.9 MPa和51.4 MPa。

图11为90°弯头的受力计算图。文献[17]给出了弯头任意点处的内压环向应力解析式,即

(a)管内压力为1.0 MPa (b)图8a工况下按第2节设置土弹簧 (c)图8b工况下增加120 ℃温升荷载图9 弯头位移等值分布图

图10 仅有内压作用时弯头环向应力分布

(2)

式中:R为弯头的曲率半径;ri为管道内半径;Di为管道内径;Pd为内压力;θ为弯头上任意点与截面内外侧分界面的夹角。

计算得到弯头内拱(e点)、外拱(a点)和顶部(n点)处的内压环向应力分别为62.5 MPa、43.75 MPa和50 MPa。这3处的模拟结果与解析计算结果的偏差分别为1.92%、1.94%和2.80%,吻合较好,表明该有限元模型适用于弯头的应力计算。

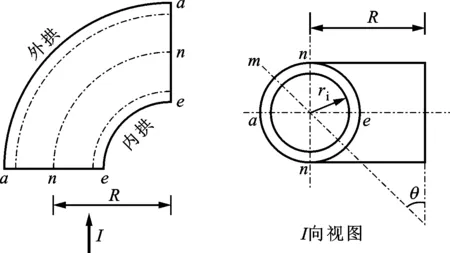
nn面为弯头内外侧分界面图11 弯头受力计算图

3.2 长臂弯头应力简化分析

温升作用下管道由于热胀冷缩产生与土壤之间的相对位移,从而产生摩擦力。在一定的温升作用下,当弯头的臂长增加到一定长度时,管道受到的轴向摩擦力与弯头反力之和等于热膨胀内力,弯臂的活动段长度达到最大值(即最大过渡段长度),此时的弯臂端头为锚固点。继续增加弯臂长度,锚固点之后的管段不再有轴向摩擦力作用,称为自然锚固段。

3.2.1 弯头管段臂长的分析 根据过渡段弯头位移矢量分析结果(图12,对应图9c),弯头附近区域位移矢量的横向分量很大,而远离该区域后位移矢量的横向分量明显减小,说明远离弯头的弯臂上横向土弹簧作用很小。竖向位移分析也有同样的规律。

Kim等的模拟分析表明,对于非直埋情况,弯臂长度大于5倍曲率半径即可消除接管长度的影响[18]。在直埋情况下,弯臂受到周围土壤的束缚,产生边缘效应的弯臂长度应该更短。图12b给出了5倍曲率半径处的位移矢量分布。可以看出,位移矢量主要沿轴向分布,且垂直于轴向的方向上位移矢量基本对称分布,说明横向土压力和竖向土压力没有产生明显的作用。5倍曲率半径以外的弯臂上这一现象更加明显。因此,对于5倍曲率半径以外的弯臂,可以只计算轴向土壤作用(即摩擦力作用)。这样,只需要按不小于5倍曲率半径长度为弯臂长度建立有限元模型,两臂施加相应的约束条件,即可进行各种长度弯头管段的计算。

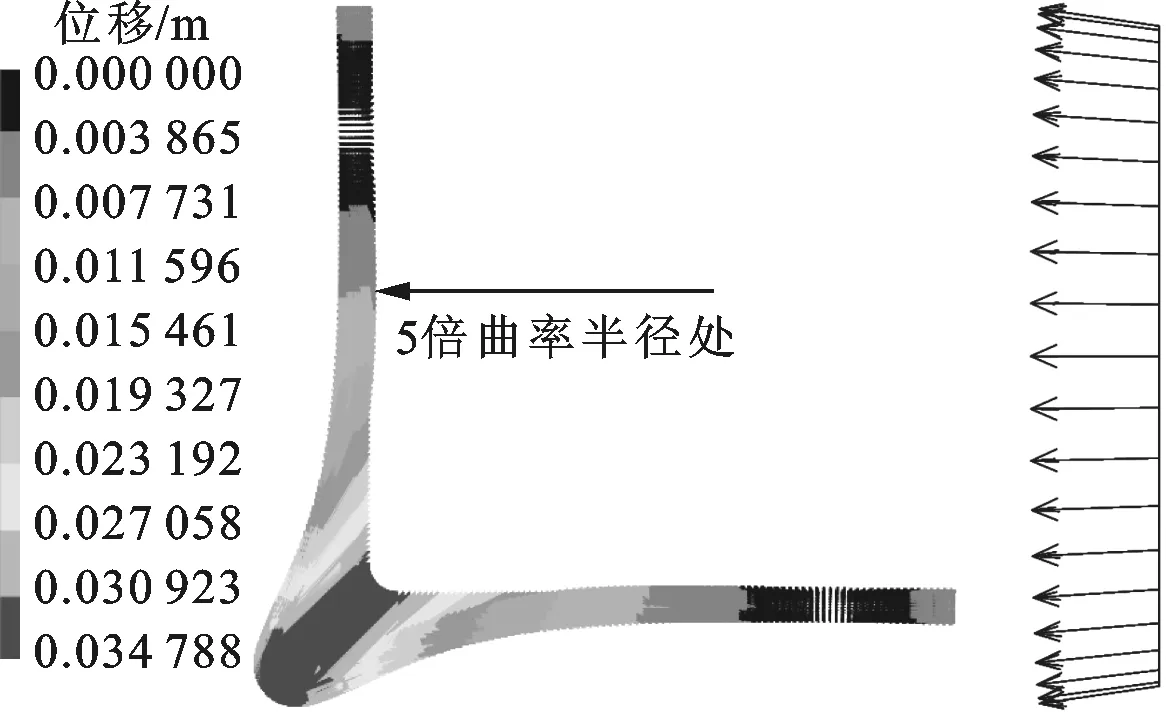
(a)总体矢量图 (b) 5倍曲率半径处位移矢量放大图图12 过渡段弯头管段的位移矢量图

3.2.2 弯臂施加约束条件的分析 如图13所示,直埋弯头管段在温升作用下向弯头处伸长,受到土壤和弯头自身弹性力的作用产生了相应的反力Fr,同时向弯头方向产生了轴向位移,从而产生了背离弯头方向的轴向摩擦力Ff。根据轴向受力平衡可知,Fr+Ff=F。

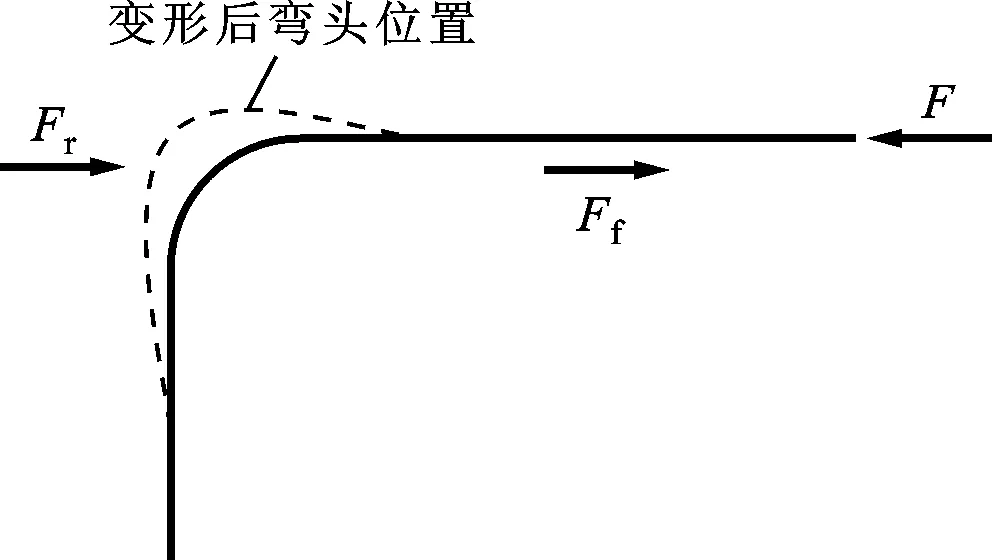
图13 直埋弯管变形简图

在计算之前Fr的大小未知,F值的大小无法确定,即弯臂处的轴力未知,因此考虑施加位移荷载作为边界条件。

弯头管段在供热管道中常兼作自然补偿器,在弯臂自然锚固点之外设置固定墩或由土力形成自然锚固。图14为直埋弯管受力简图,G为固定点,O为自然锚固点,B为静摩擦与动摩擦的分界点(对应图2的轴向弹簧曲线折点),OC之间为过渡段,OB之间为静摩擦段,OG之间为自然锚固段。

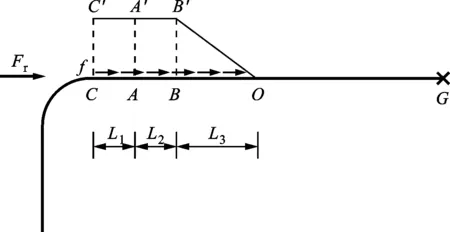
图14 直埋弯管受力简图

取图14中A点左侧为简化后的模拟管段,考虑在A点施加位移荷载ΔL作为约束条件。

根据力的平衡,可得

FB=FA+fL2

(3)

FO=FA+fL2+fL3/2

(4)

式中:FA、FB、FO为A、B、O点的轴向力。

图15为弯臂上的应变分布。OAA′O围成的面积所代表的位移值即为在A点施加的位移荷载ΔL,该面积分解为BAA′B′B和OBB′O两部分。

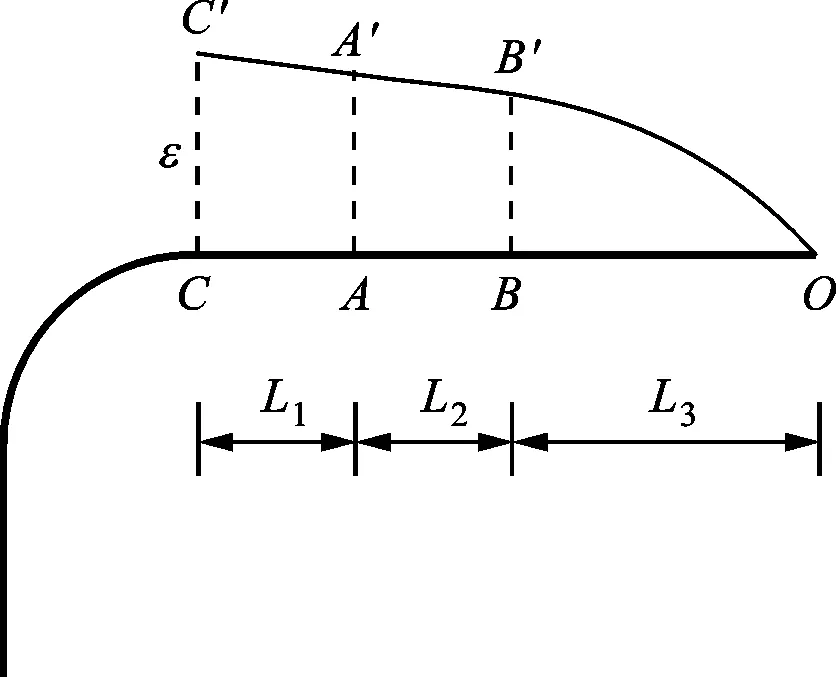
图15 弯臂上的应变分布

BAA′B′B面积为

(5)

式中:α为钢管的线膨胀系数;E为钢材的弹性模量;S为钢管壁的横截面积;ΔT为管道的温升;l为管长度。

OBB′O的面积为

(6)

可见,ΔL3即为图2中的轴向屈服位移u。

式(5)、式(6)积分得

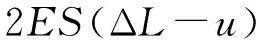
(7)

(8)

模拟中将ΔL作为已知量输入,通过有限元分析可以得到A点的轴力FA。将ΔL、FA代入式(7)、(8)可以得到对应A点位移荷载为ΔL时的L2和L3,进而得到弯臂过渡段长度为L=L1+L2+L3。

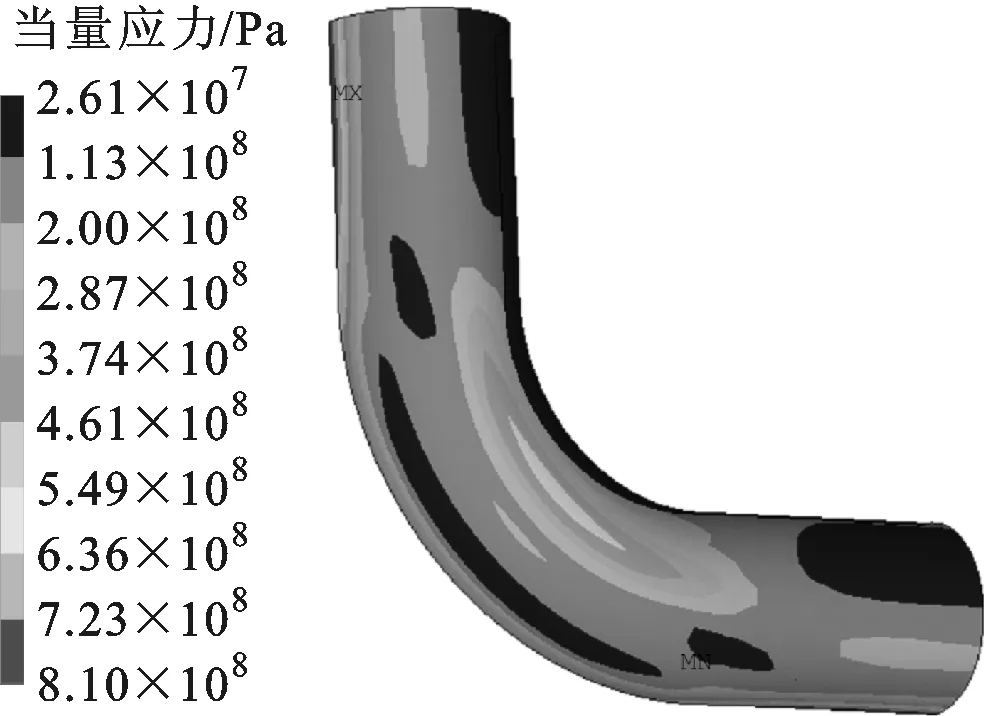
(a)简化模型应力分布

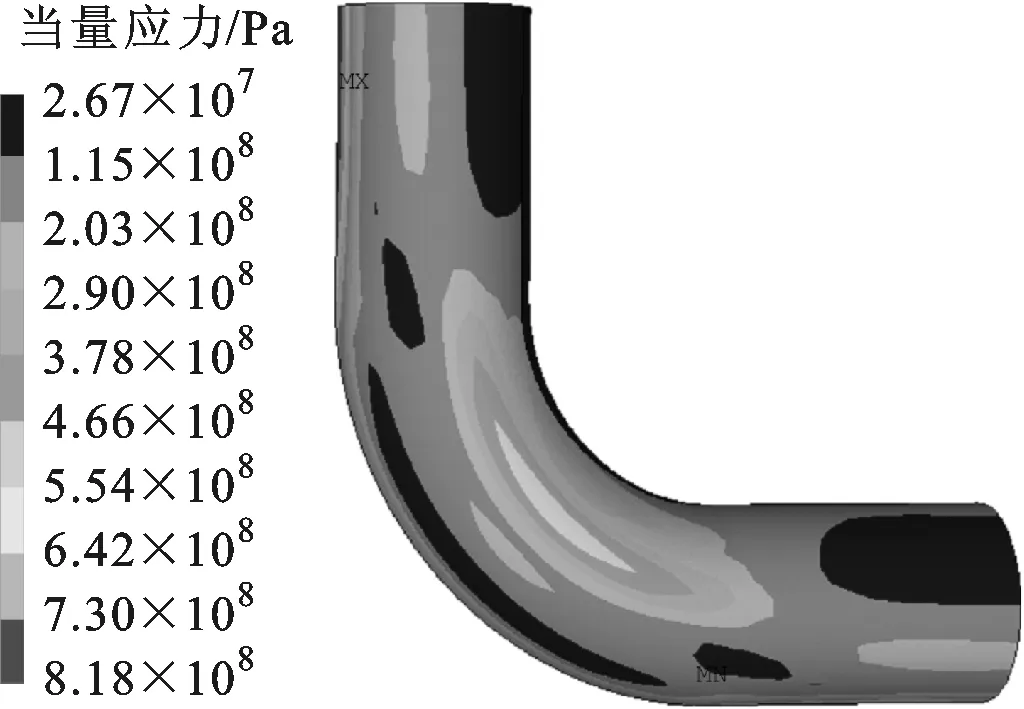
(b)全尺寸模型应力分布图16 简化模型与全尺寸模型当量应力对比

3.2.3 简化方法的验证 以臂长为40 m的弯头模型为基础,假定两臂施加的轴向位移为50 mm。应力分析结果见图16,图16a中最大当量应力为810 MPa。模拟得到A点的轴力为2 077 kN,代入式(7)、(8)得到L2=41.05 m、L3=17.70 m,从而全尺寸模型为L=98.75 m。为了对比验证,对臂长为L=98.75 m的全尺寸模型进行模拟(两臂施加的位移为0),结果见图16b,其中最大当量应力为818 MPa,与40 m臂长的简化模型相比,误差为1%,且当量应力分布也十分吻合。以上对比说明,用缩短臂长、两臂施加轴向位移的方法可以作为全尺寸模型的简化模型,从而显著减小计算量。

另外,采用弹性抗弯铰解析方法[1]得到最大当量应力为702 MPa,与全尺寸模型结果比较,偏差为-14%,可算基本吻合,但是弹性抗弯铰法不能给出弯头的应力分布。

4 弯管应力的影响因素

4.1 一次应力的影响因素

一次应力的影响因素为内压、管道壁厚、弯头曲率半径(与弯头的公称直径D有关)和管道埋深。

由图17和图18可以看出,一次应力随壁厚、管道埋深的增加而降低,随内压、弯头曲率半径的增加而增加。90°对焊弯头(弯头曲率半径为0)在对焊区域产生了较大的峰值应力。

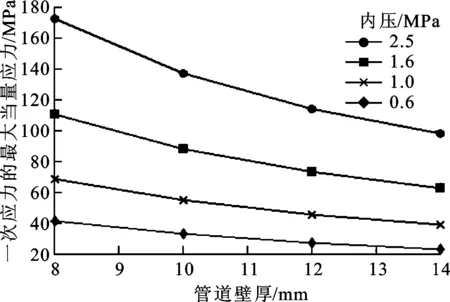
图17 内压和壁厚对一次应力的影响

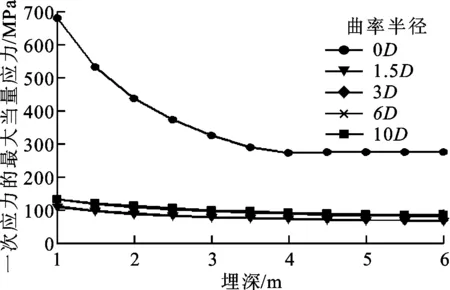
图18 曲率半径和埋深对一次应力的影响

4.2 二次应力的影响因素

根据应力分类法,二次应力为位移导致的应力,因此影响弯头位移的因素都会对二次应力产生影响。二次应力的影响因素除内压、管道壁厚、弯头曲率半径和管道埋深外,还有温升和弯头端部位移。

图19、20、21给出了弯头二次应力的影响因素分析。从图中可以看出,二次应力随壁厚的增加而降低,随内压、埋深(R=0D的90°对焊弯头除外)、温升、弯头曲率半径、弯头端部位移的增加而增大。

图19中二次应力的最大当量应力随管道壁厚的变化接近直线,表明二次应力与壁厚为近似线性关系,各压力下的变化近似平行,表明二次应力与内压为近似线性关系;图20中不同温升下的曲线较为靠近,表明在弯头端部位移相同的情况下,温升对二次应力影响较小;图21中90°对焊弯头(弯头曲率半径R=0D)二次应力的最大当量应力数值较高,表明在对焊区域产生了较大的峰值应力,且随埋深增加而减小。

图19 内压和壁厚对二次应力的影响

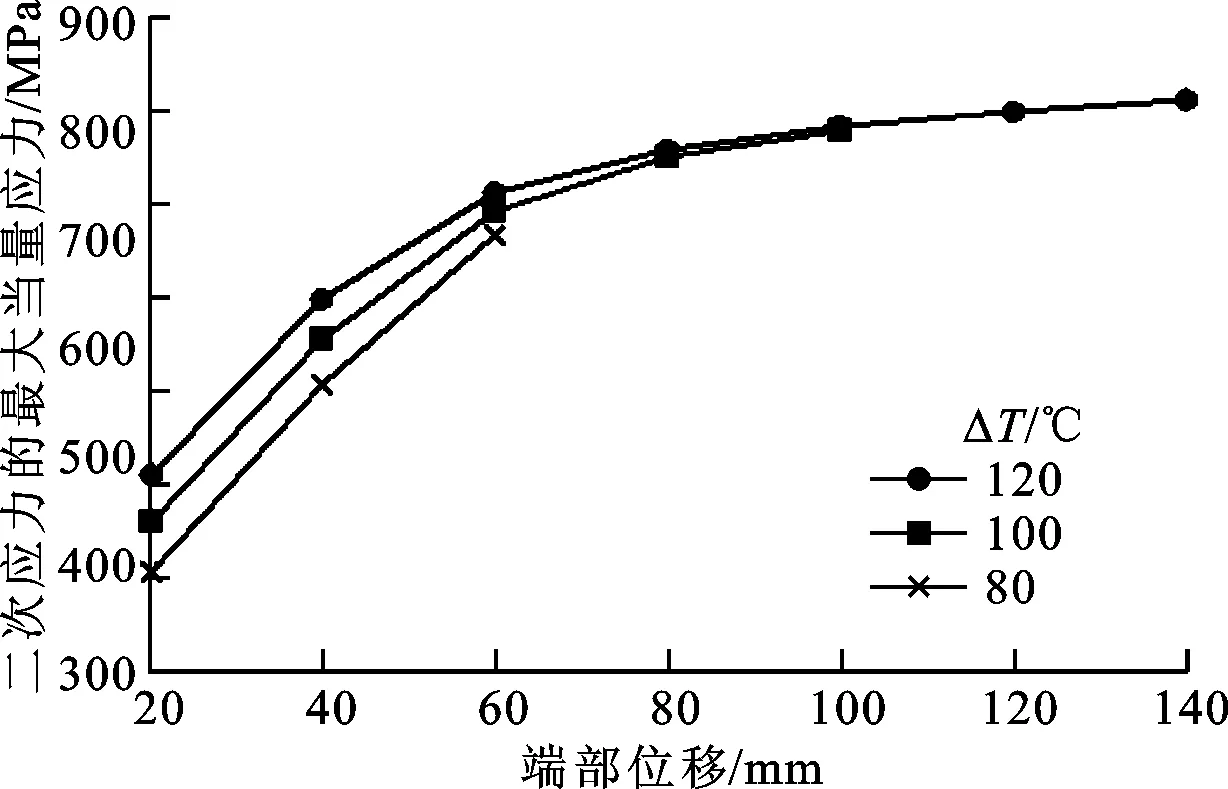
图20 温升和弯头端部位移对二次应力的影响

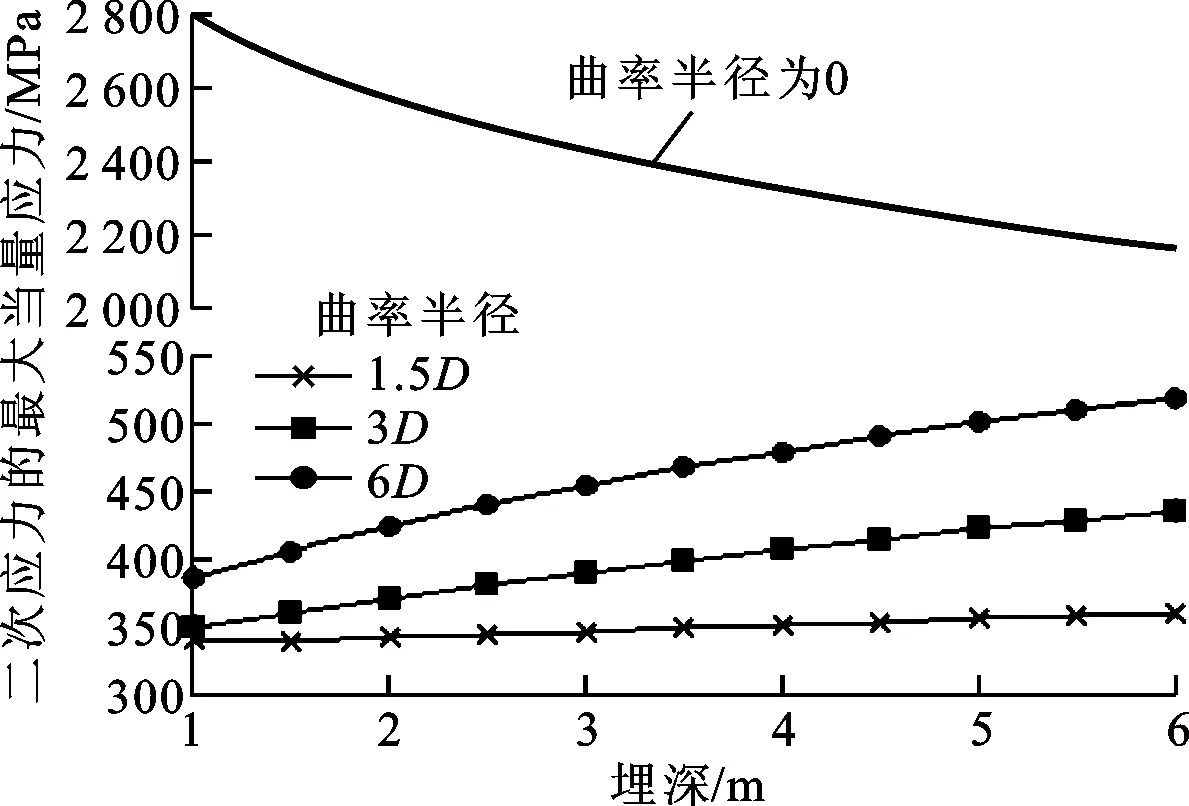
图21 曲率半径和埋深对二次应力的影响

4.3 弯头截面椭圆化的影响

设定弯头横向椭圆化10%(横向为椭圆长轴,长度为标准管径的1.1倍),竖向椭圆化-10%(竖向为椭圆短轴,长度为标准管径的0.9倍),其他设置同图8c、9c对应工况,模拟结果见图22a、22c;设定弯头横向椭圆化-10%,竖向椭圆化10%,其他设置同3.2.1节,模拟结果见图22b、22d。

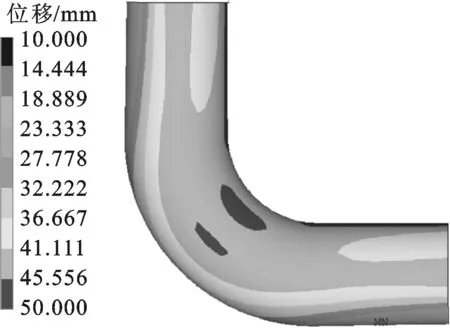
(a)横向椭圆化位移等值分布

(b)竖向椭圆化位移等值分布

(c)横向椭圆化当量应力分布

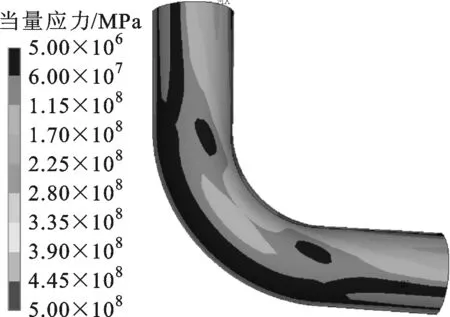
(d)竖向椭圆化当量应力分布图22 弯臂端头处于自由状态下椭圆弯头的应力分布

与图8c、9c未椭圆化弯头的模拟结果相比(见表3),弯头横向椭圆化(椭圆长轴在横向)可使弯头的最大位移和最大当量应力大大增加;竖向椭圆化(椭圆长轴在竖向)可使弯头的最大位移和最大当量应力略有所下降。因此,考虑管土之间的三维相互作用后,对于水平敷设的直埋弯头管段,竖向椭圆化是有利的,而横向椭圆化是有害的。

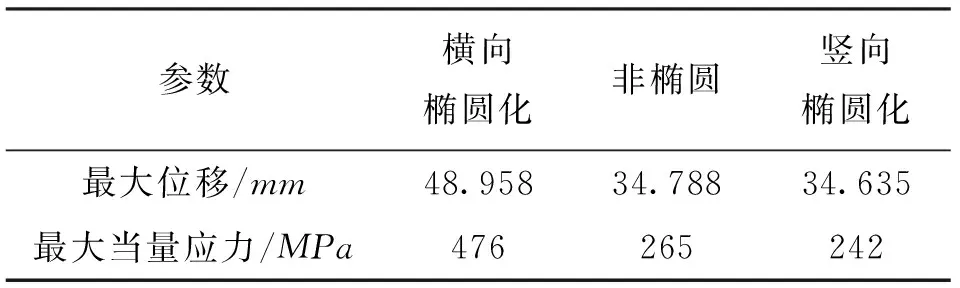
表3 椭圆弯头与非椭圆弯头的应力分析结果对比

4.4 地面荷载的影响

地面人群荷载、地面堆积荷载和地面车辆荷载均会影响管道所受压力,本文通过调整土弹簧刚度(修改屈服力)来模拟地面荷载的影响。

地面人群荷载标准值取4kN/m2,准永久值系数取0.3;地面堆积荷载标准值取10kN/m2,准永久值系数取0.5[19]。计算时这两项可直接以准永久值叠加到土压力上。

文献[20]规定:“道路路面结构设计应以双轮组单轴载100kN为标准轴载,双轮组单轴载为100kN,轮胎压强为0.7MPa,单轴轮迹当量圆半径r为10.65cm,双轮中心间距为3r”。

按照分布角法[21]进行管顶地面车辆荷载产生的附加土压力进行计算,双轮在地面下H深度处产生的竖向应力标准值为

(9)

式中:μd为车辆轮压的动载系数,覆土深度大于0.7 m时取1.0;Qk为标准轴载;β为压力扩散角,取30°。

通过计算得到,地面车辆荷载标准值为10.2 kN/m2,地面车辆荷载的准永久值系数取0.5[19],从而地面人群荷载、地面堆积荷载和地面车辆荷载引起的竖向土压力的附加荷载qadd=11.3 kN/m2。

结合第1.2节土弹簧参数的取值,对土弹簧的屈服力进行调整,即在原屈服力的基础上增加地面荷载引起的附加值。

轴向弹簧的屈服力附加值为

(10)

式中:μ为管道与土壤之间的摩擦系数;K0为土壤静压力系数;D′为保温管外径。

横向弹簧的屈服力附加值为

(11)

式中:Kq为土压力系数。

竖向弹簧的屈服力附加值为

(12)

式中:N为土壤承载系数。

对弯臂长度为20 m的弯头管段进行分析时,同时对管道施加内压(1.0 MPa)和温升荷载(120 ℃),弯臂端头施加130 kN的力荷载,管道周围设置土弹簧,按式(10)～式(12)增加地面荷载,由此得到的结果见图23。

相比于未设置地面荷载的模拟结果(图8c、9c),增加地面荷载后,最大位移由34.788 mm减小为10.275 mm,最大当量应力由265 MPa减小为208 MPa。

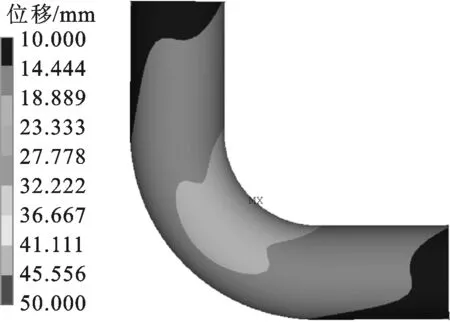
(a)位移等值分布

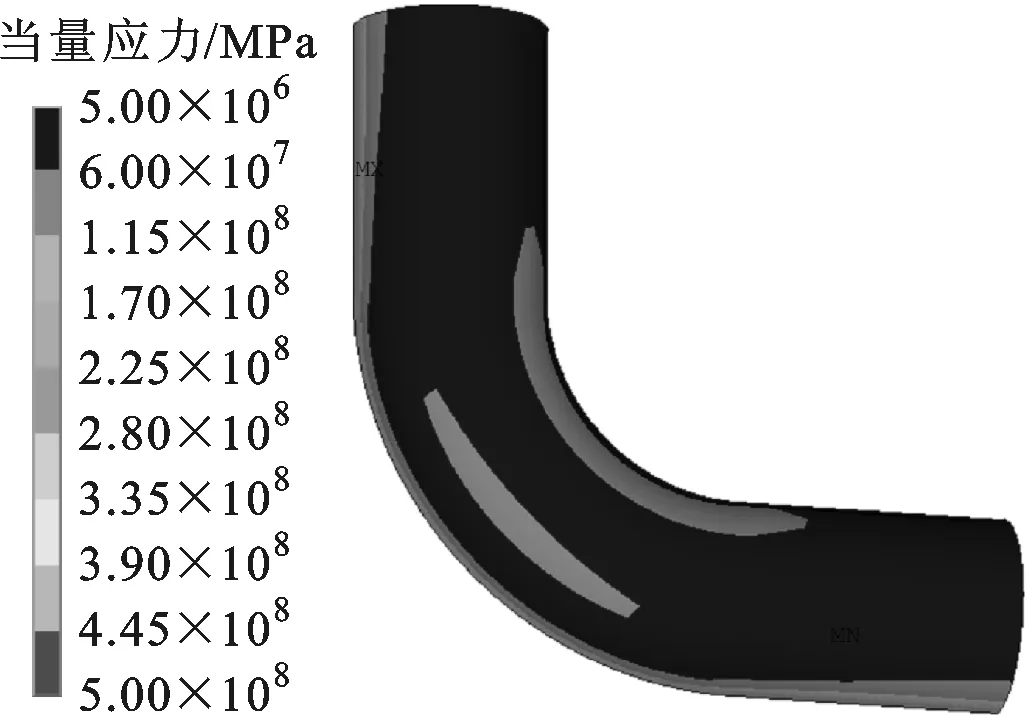
(b)当量应力分布图23 地面荷载作用下弯管应力分布

5 结 论

本文应用ANSYS软件,通过在弯头管段设置轴向、横向和竖向土弹簧,对弯臂端头施加相应的边界条件,建立了弯管的三维热-力耦合有限元模型,对直埋热水供热管道弯管在内压和温升荷载作用下的应力分布特性进行了热-力耦合分析,提出了简化弯臂长度的有限元分析模型。通过计算分析,得出如下结论。

(1)内压、土壤作用下弯头管段的应力和位移均较小,增加温升荷载后,位移明显增加,管土作用增强,当量应力增加。

(2)温升荷载作用下,弯臂对弯头的热作用可以采用位移荷载等效替代,等效后弯臂长度应不小于5倍管径,并以轴向位移来替代被缩短掉的弯臂的轴向作用。

(3)内压、土壤作用下,弯头一次应力随壁厚、管道埋深的增加而降低,随内压、弯头曲率半径的增加而增加;增加温升荷载后,弯头二次应力随壁厚的增加而降低,随内压、埋深、温升、弯头曲率半径、弯头端部位移的增加而增加。

(4)温升荷载作用下,竖向椭圆化对弯头是有利的,横向椭圆化是有害的。地面荷载作用使弯头最大当量应力降低,对弯头起到了保护作用。

[1] 中华人民共和国住房和城乡建设部. CJJ/T 81—2013城镇供热直埋热水管道技术规程 [S]. 北京: 中国建筑工业出版社, 2013.

[2] PENG L. Stress analysis methods for underground pipe lines: part Ⅱ [J]. Pipe Line Industry, 1978, 47(5): 65-75.

[3] 崔孝秉. 埋地长输管道水平弯头的升温荷载近似分析 [J]. 华东石油学院学报, 1978(2): 54-68. CUI Xiaobing. Approximation analysis on temperature load of horizontal elbow in buried long-distance pipeline [J]. Journal of East China University of Petroleum, 1978(2): 54-68.

[4] 董俊华, 高炳军, 张及瑞. 热推制90°弯头的壁厚分布规律及其应力分析 [J]. 压力容器, 2010, 27(12): 45-48, 32. DONG Junhua, GAO Bingjun, ZHANG Jirui. Wall thickness distribution and stress analysis of heat pushing 90° elbow [J]. Pressure Vessel Technology, 2010, 27(12): 45-48, 32.

[5] 杜保存. 大口径供热直埋椭圆弯头的有限元分析 [D]. 太原: 太原理工大学, 2012.

[6] 刘波. 无缺陷90°弯头应力状态的有限元分析 [J]. 中国石油和化工标准与质量, 2012, 32(6): 75-76. LIU Bo. Finite element analysis on stress state of frictionless 90° elbow [J]. China Petroleum and Chemical Industry Standards and Quality, 2012, 32(6): 75-76.

[7] 黄鉴, 马业华. 燃气管道弯头应力分布及塑性极限荷载分析 [J]. 煤气与热力, 2012, 32(10): B01-B03. HUANG Jian, MA Yehua. Analysis on stress distribution and plastic limit load of elbows in gas pipeline [J]. Gas & Heat, 2012, 32(10): B01-B03.

[8] 张鹏, 李晓红. 内压和弯矩联合作用下理想弯头的有限元分析 [J]. 焊管, 2014, 37(2): 14-17. ZHANG Peng, LI Xiaohong. Finite element analysis on ideal elbow under combined effect of inner pressure and bending moment [J]. Welded Pipe and Tube, 2014, 37(2): 14-17.

[9] 王国伟. 大口径直埋供热管道90°弯头疲劳寿命的有限元分析 [D]. 太原: 太原理工大学, 2010.

[10]SELVADURAL A. 土与基础相互作用的弹性分析 [M]. 范文田, 等译. 北京: 中国铁道出版社, 1984.

[11]WINKLER E. Theory of elasticity and strength [M]. Prague, Czechoslovakia: Dominicus, 1867.

[12]European Committee for Standardization. BS EN 13941—2009 Design and installation of preinsulated bonded pipe systems for district heating [S]. London, UK: Standards Policy and Strategy Committee, 2009.

[13]American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design [M]. Washington, DC, USA: American Petroleum Institute Production Department, 2002: 61-63.

[14]American Lifelines Alliance. Guidelines for the design of buried steel pipe [M]. New York, USA: American Sociefy of Civil Engineering, 2001.

[15]王新敏, 李义强, 许宏伟. ANSYS结构分析单元与应用 [M]. 北京: 人民交通出版社, 2011.

[16]中国市政工程华北设计研究院. 05系列建筑标准设计图集 [M]. 北京: 中国建筑工业出版社, 2005: 62.

[17]王致祥, 梁志钊, 孙国模, 等. 管道应力分析与计算 [M]. 北京: 水利电力出版社, 1983.

[18]KIM Y, OH C. Limit loads for pipe bends under combined pressure and in-plane bending based on finite element limit analysis [J]. International Journal of Pressure Vessels & Piping, 2006, 83(2): 85-90.

[19]中华人民共和国建设部. GB 50332—2002 给水排水工程管道结构设计规范 [S]. 北京: 中国建筑工业出版社, 2003.

[20]中华人民共和国住房和城乡建设部. CJJ 37—2012 城市道路工程设计规范 [S]. 北京: 中国建筑工业出版社, 2012.

[21]王直民. 交通荷载作用下埋地管道的力学性状研究 [D]. 杭州: 浙江大学, 2006.

(编辑 苗凌)

Thermal-Mechanical Coupled Analysis for Right Angle Bend of Directly Buried Heating Pipeline

JIANG Chao1,GUAN Yanling1,DENG Shunxi1,MENG Qinglong1, SHI Juanling2,CAO Honglin2

(1. School of Environmental Science and Engineering, Chang’an University, Xi’an 710054, China; 2. Parent Company of Xi’an District Heating, Xi’an 710016, China)

Aiming at the complicated stress characteristics of bends in directly buried heating pipelines, a three-dimensional thermal-mechanical coupled finite element model was constructed in terms of soil spring model. The main affecting factors on stress distribution of directly buried bends were analyzed. A thermal-mechanical coupled finite element model for bend with reduced straight pipe lengths was given. The weights of thermal medium and covering soil were considered in the pipe-soil interaction of the model. The boundary conditions were exerted to the ends of two bend arms. The results indicate that buried elbows of bends bear peak stresses with considerably higher value due to temperature rise than due to internal pressure. The primary stress of buried bend decreases with the increasing pipe wall thickness and buried depth, while it increases with the increasing internal pressure and curvature radius. The secondary stress of buried bend decreases with the increasing pipe wall thickness, while it increases with the increasing internal pressure, buried depth, temperature rise, curvature radius and end displacements of bend arms. Vertical ovalization for pipe section is beneficial to the bend, but transverse ovalization is harmful. The ground load reduces the maximum equivalent stress in buried bend.

directly buried heating pipeline; bend; stress; thermal-mechanical coupled analysis; finite element model

10.7652/xjtuxb201605019

2015-11-30。 作者简介:江超(1984—),男,博士生;官燕玲(通信作者),女,教授,博士生导师。 基金项目:国家自然科学基金青年基金资助项目(51208059);陕西省科学技术研究发展计划资助项目(2013K13-02-01);陕西省住房和城乡建设厅科学技术计划项目(2014-04)。

时间:2016-03-01

http:∥www.cnki.net/kcms/detail/61.1069.T.20160301.1016.008.html

TU995

A

0253-987X(2016)05-0125-09