平行轴渐开线变厚齿轮传动的几何设计与啮合特性分析

倪高翔,朱才朝,宋朝省,刘怀举

(重庆大学机械传动国家重点实验室,400030,重庆)



平行轴渐开线变厚齿轮传动的几何设计与啮合特性分析

倪高翔,朱才朝,宋朝省,刘怀举

(重庆大学机械传动国家重点实验室,400030,重庆)

基于空间齿轮啮合理论,建立了平行轴渐开线变厚齿轮传动的节圆锥设计模型,提出了平行轴渐开线变厚齿轮传动的几何设计方法。考虑安装误差与变形,建立了平行轴渐开线变厚齿轮啮合分析模型,研究了节锥角、载荷与安装误差对啮合特性的影响规律。结果表明:节锥角增加使接触压力减小、齿轮副传动精度降低,但啮合刚度波动更为平缓;载荷增加使角度传递误差均值与峰峰值均增加,但对啮合刚度均值的影响不大;安装误差中,轴线平行度安装误差对齿轮副的啮合特性影响较大,将导致齿轮副产生边缘接触,而对于相同的轴线平行度误差量,y方向的轴线平行度误差产生的边缘接触更加严重。研究结果可望为平行轴渐开线变厚齿轮传动的工业化推广提供理论依据。

渐开线变厚齿轮;平行轴;节圆锥设计;啮合特性;安装误差

渐开线变厚齿轮因沿轴线方向的变位系数呈线性变化,导致齿形在轴线方向上有一定的锥度,通过调整轴向位移补偿间隙可实现精密传动;根据安装方式不同,可实现平行轴、交错轴、相交轴传动。渐开线变厚齿轮已广泛应用于高速游艇、精密机器人和全驱动汽车等领域。

国内外对渐开线变厚齿轮传动开展了大量研究,取得了许多有价值的研究成果。Tsai等研究了变厚齿轮传动的几何设计方法,并对近似线接触的斜锥形齿轮副进行了承载接触分析[1-2]。李瑰贤等对平行轴内啮合变厚齿轮副进行了几何设计,并对相交轴变厚齿轮的齿形误差与轴线误差进行了计算[3-4]。林超等对标准安装和考虑安装误差情况下的平行轴斜齿变厚齿轮进行了轮齿接触分析,得出了该类传动对轴线安装误差较敏感的结论[5]。Brecher等对计算平行轴变厚齿轮齿根承载能力的2种仿真方法进行了描述,并通过疲劳试验进行了对比研究[6]。朱才朝等基于节圆锥啮合理论,考虑近似线接触条件,建立了相交轴、交错轴变厚齿轮传动啮合模型,对其几何设计与啮合特性等方面进行了研究[7-10]。Trong等通过完全弹性多体方法对变厚齿轮的接触特性进行了研究[11]。Liu等建立了交错和平行轴变厚齿轮啮合模型,并对避免根切的条件进行了研究[12-13]。

本文基于节圆锥啮合理论,建立了平行轴变厚齿轮节圆锥模型,研究了节锥角、载荷以及安装误差对其啮合特性的影响,以期为平行轴渐开线变厚齿轮传动的工业化推广提供理论依据。

1 基于节圆锥的渐开线变厚齿轮几何设计

图1所示为变厚齿轮工作节圆锥简图[8],其中M为节圆锥上的点,ni为其单位法矢量,γwi为工作节锥角,θi为其在xi-yi平面内的展角。M点的坐标Rwi在坐标系Si(i=1,2)中可表示为

(1)

M点的单位法矢量ni可表示为

(2)

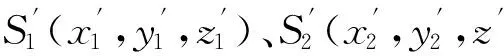
图1 工作节圆锥

图2 平行轴渐开线变厚齿轮节圆锥模型

两节圆锥在P点的接触方程为

(3)

可以得到如下方程组

(4)

式中

(5)

通过式(4)可以得到两锥角的关系式

(6)

以及E与d1的表达式

(7)

(8)

若图2中两母线的夹角为φ,则其满足如下关系式

(9)

联立式(2)、(4)、(8)、(9)可得

(10)

由于两节圆锥大端为异侧,所以两节圆锥的工作螺旋角应满足如下关系式

(11)

定义变厚齿轮端面齿形角系数[1]

(12)

式中:cosαtL(R)wi为齿轮左(右)端面工作节圆压力角;cosαtL(R)i为齿轮左(右)端面参考节圆压力角;mn为变厚齿轮的法向模数;Ni为变厚齿轮的齿数;rPi为齿轮参考节圆的压力角,rPi=Nimn/(2cosβi)。从而得到法面齿形角系数

(13)

根据渐开线齿轮正确啮合的条件[12],得到如下公式

(14)

(15)

式中:αnw为公共齿条压力角;mnw为公共齿条法向模数;βi为齿条刀具齿线倾斜角;γi为齿轮节锥角。

根据无侧隙啮合方程[15]

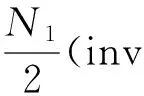
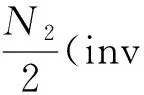
(16)

可得到另一齿轮的端面变位系数。式中:xt1、xt2分别为两齿轮的端面变位系数。

根据上述推导,建立平行轴渐开线变厚齿轮的几何设计流程,如图3所示。其中,中心距E,2个齿轮的齿数N1、N2及节锥角γ1、γ2,法向模数mn和压力角αn,齿轮1的齿条刀具齿线倾斜角β1以及节端面变位系数xt1为已知参数,法面齿形角系数ξn和齿轮2的齿条刀具齿线倾斜角β2为待求变量。

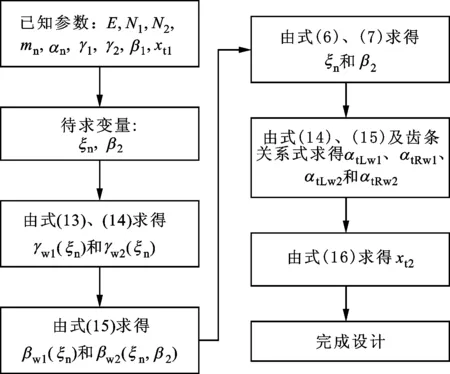
图3 平行轴渐开线变厚齿轮的几何设计流程图

2 平行轴渐开线变厚齿轮传动的啮合分析模型

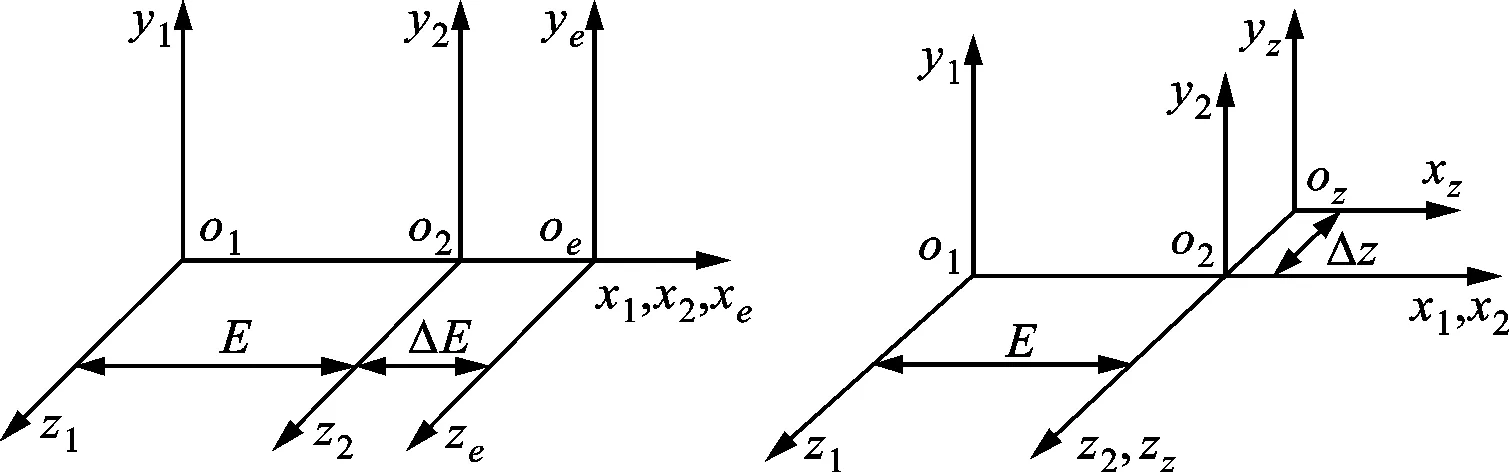
(a)中心距误差 (b)轴向位置误差

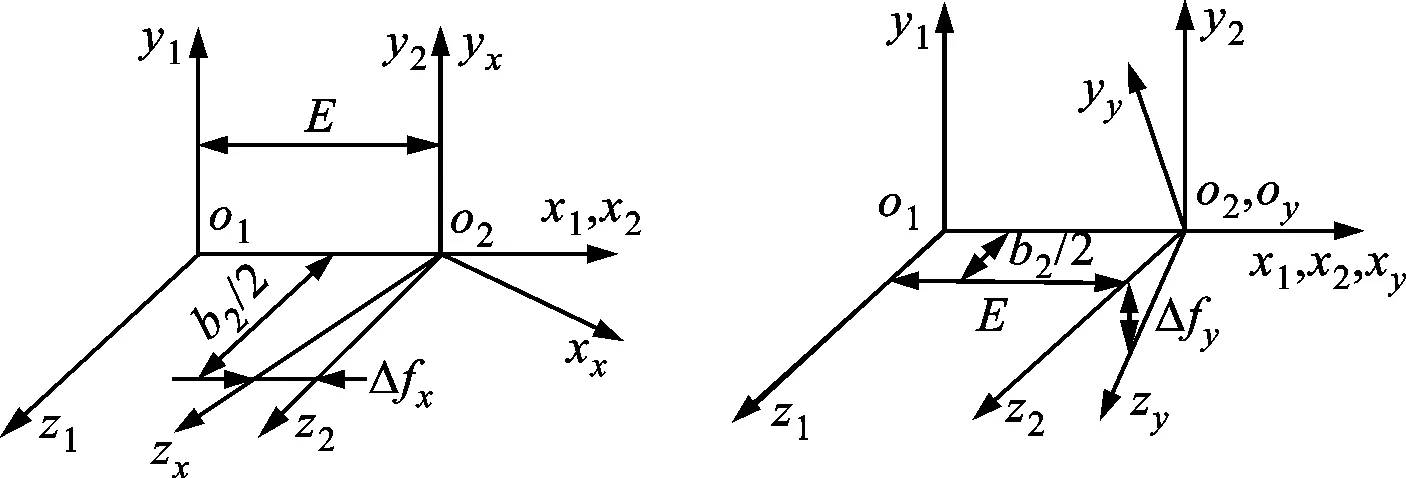
(c)x方向轴线平行度误差 (d)y方向轴线平行度误差图4 平行轴渐开线齿轮副安装误差示意图

结合实际啮合工况,定义平行轴渐开线变厚齿轮副的安装误差,如图4所示。其中,S1(x1,y1,z1)、S2(x2,y2,z2)分别为标准安装时小齿轮与大齿轮所在的坐标系,Se(xe,ye,ze)、Sz(xz,yz,zz)、Sx(xx,yx,zx)和Sy(xy,yy,zy)分别为齿轮副产生中心距误差、轴向位置误差、x方向轴线平行度误差和y方向轴线平行度误差时大齿轮所在的坐标系。

定义实际中心距与标准安装中心距的误差为中心距安装误差ΔE,如图4a所示;定义齿轮沿其轴线移动所产生的误差为轴向位置安装误差Δz,如图4b所示;当两齿轮的轴线不平行时将产生轴线平行度误差,若齿轮轴线绕y轴旋转,将产生x方向的轴线平行度误差Δfx,如图4c所示;若齿轮轴线绕x轴旋转,将产生y方向的轴线平行度误差Δfy,如图4d所示。图4中所示的安装误差均为正向。

根据平行轴渐开线变厚齿轮节圆锥的设计方法,得到表1所列的齿轮副几何设计参数。考虑安装误差,基于有限元法建立平行轴渐开线变厚齿轮啮合模型(使大齿轮大端与小齿轮小端相啮合),如图5所示,并在有限元软件Abaqus中进行平行轴渐开线变厚齿轮副接触特性分析。

表1 平行轴变厚齿轮副几何设计参数

(a)齿轮副啮合实体模型 (b)网格划分

图5 平行轴渐开线变厚齿轮副啮合模型

齿轮啮合模型选用的材料为17CrNiMo6,其弹性模量为208 GPa,泊松比为0.298。因为渐开线变厚斜齿轮左、右齿面的螺旋角和压力角均不相同,所以当主动轮的旋转方向不同时,分析结果也会不一样。本文选取小齿轮为主动轮,其旋转方向从小端看为逆时针方向。对主动轮施加转角,使其转过4个齿的角位移1.256 rad;对从动轮施加负载转矩500 N·m。将计算过程中相互接触的5对齿面定义成接触对,接触方式为无摩擦。划分网格时,采用全六面体网格类型,将接触对所在齿面划分较密的网格,对其余部分划分较粗的网格。选择的输出量有2个齿轮的转角、接触应力和接触力矩等。

3 平行轴渐开线变厚齿轮传动的啮合特性分析

3.1 节锥角对啮合性能的影响

合理选择节锥角的大小十分关键:当选取的节锥角过小时,可能导致变厚特征不明显,达不到预期效果;当选取的节锥角过大时,设计出来的齿轮大端有可能产生齿顶变尖现象,会降低齿顶部分的强度与刚度,影响齿轮的正常传动,还有可能造成齿面渐开线段的有效区域减少。为保证齿轮副正常工作,选取节锥角分别为6°、7°、8°、9°、10°,得到节锥角对角度传递误差和啮合刚度的影响规律,如图6、图7所示。

从图6中可以看出,随着节锥角的增加,角度传递误差的均值逐渐增大,但角度传递误差峰峰值逐渐减小,说明节锥角的增加使齿轮副的传动精度逐渐降低,但工作状态变得更加平稳。从图7中可以看出,随着节锥角的逐渐增加,啮合刚度的均值逐渐减小,但在一个啮合周期内啮合刚度波动更为平缓,这必然会减小轮齿啮合过程中的内部时变激励,改善齿轮传动的啮合平稳性。

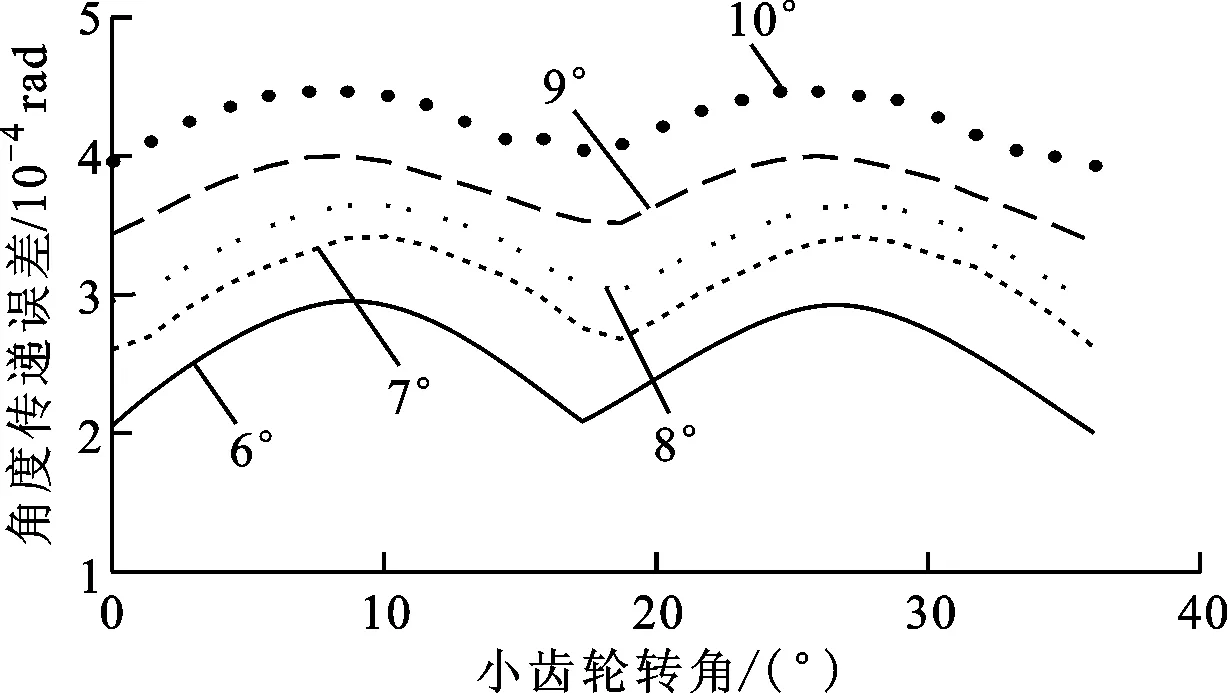
(a)角度传递误差曲线

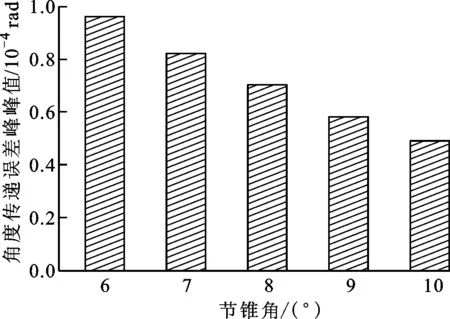
(b)角度传递误差峰峰值图6 节锥角对角度传递误差的影响

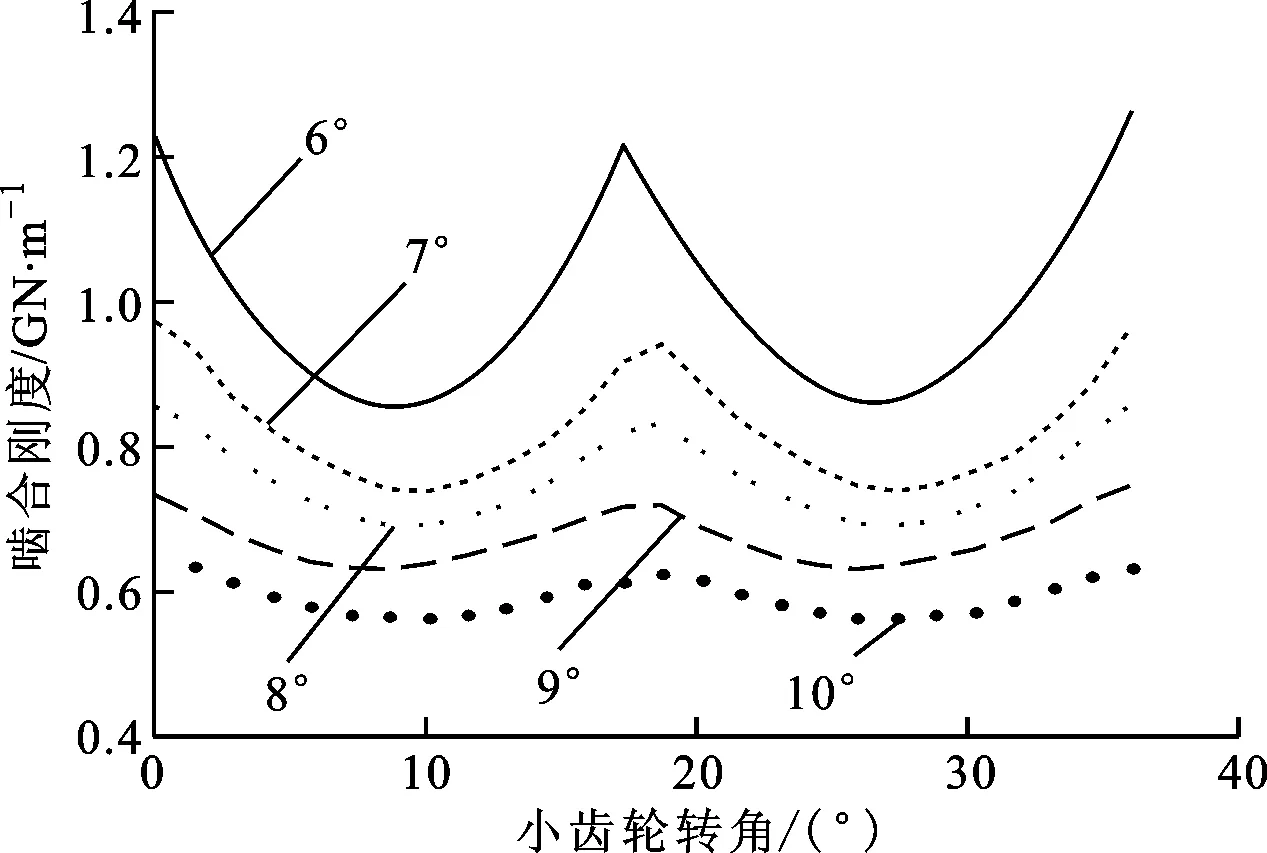
(a)啮合刚度曲线

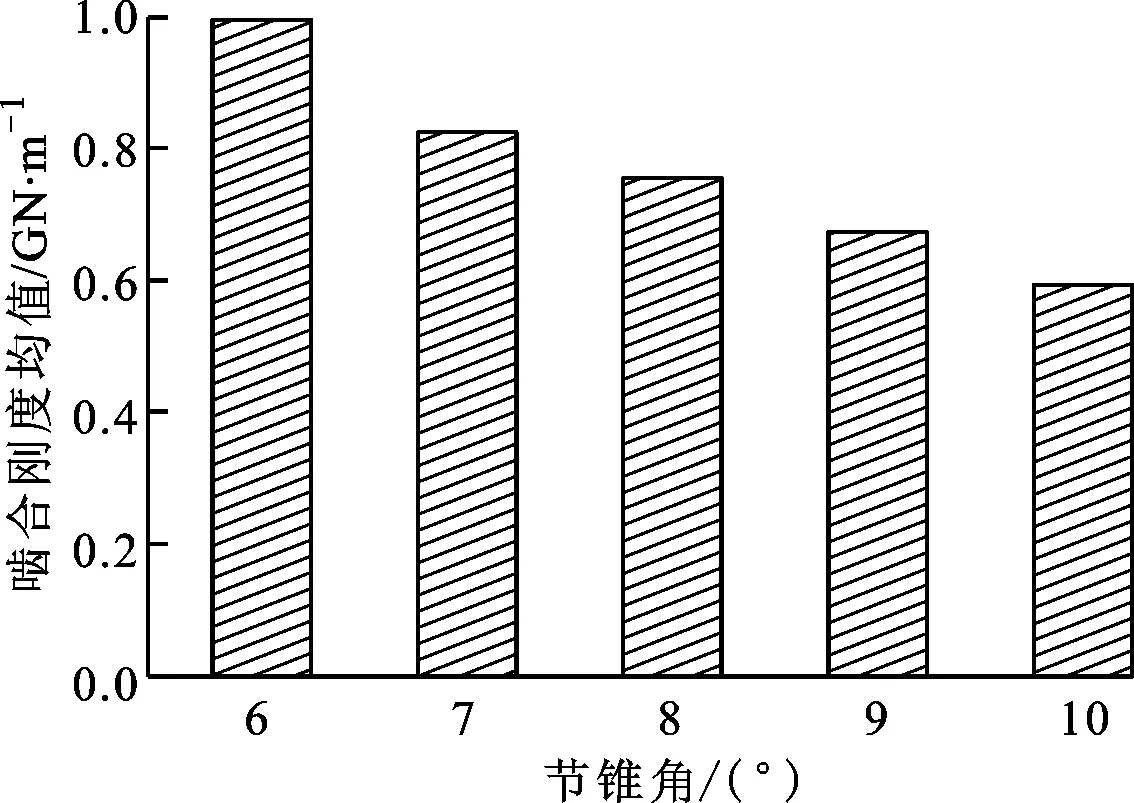
(b)啮合刚度均值图7 节锥角对时变啮合刚度的影响

(a)节锥角为6°

(b)节锥角为10°图8 节锥角对大齿轮啮合印痕及接触压力的影响

为研究节锥角的变化对啮合印痕的影响规律,选取节锥角为6°和10°两种工况进行分析,得到的大齿轮啮合印痕图如图8所示。从图中可以看出,大齿轮小端的接触压力大于大端的,且节锥角增加使得齿面最大接触压力减小,啮合印痕的形状更加倾斜。

3.2 载荷对啮合性能的影响

载荷是影响渐开线变厚齿轮传动的因素之一,研究其对平行轴渐开线变厚齿轮传动啮合特性的影响十分必要。本文选取的齿轮材料为17CrNiMo6,其屈服强度σs为835 MPa。在有限元分析中,选取载荷10～500 N·m,研究载荷变化对齿轮副啮合特性的影响规律。图9为10、500 N·m载荷下同一时刻齿面的Mises应力图,可以看出接触状态为明显的线接触,且载荷为500 N·m时的最大Mises应力为732.1 MPa。

(a)载荷为10 N·m

(b)载荷为500 N·m图9 不同载荷下齿轮齿面的Mises应力

使用相同的啮合分析模型分别计算当载荷从10 N·m提高至500 N·m时的角度传递误差和啮合刚度,结果如图10、图11所示。从图10中可以看出,随着载荷的增加,角度传递误差的均值和峰峰值均呈现明显的递增趋势,从而传动精度逐渐下降。从图11中可以看出,在轻载(10 N·m)工况下,齿面接触面积较小,导致啮合刚度较小;随着载荷的增加,齿面接触区域也逐渐增大,从而啮合刚度明显增加,但当载荷增加到一定范围后,接触区域的增幅变小,导致啮合刚度的变化也较小,原因在于平行轴渐开线变厚齿轮传动的接触类型为线接触。

(a)对角度传递误差的影响

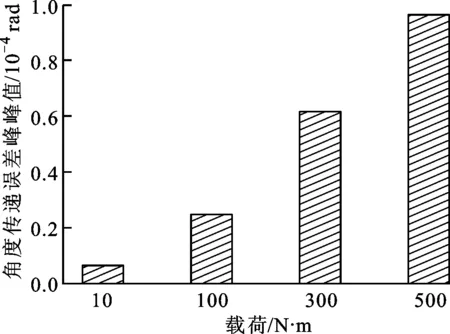
(b)对角度传递误差峰峰值的影响图10 载荷对角度传递误差及其峰峰值的影响

(a)对啮合刚度的影响

(b)对啮合刚度均值的影响图11 载荷对啮合刚度的影响

为了研究载荷对齿轮副参与啮合的区域的影响,通过Abaqus的后处理功能对不同载荷下大齿轮齿面的啮合印痕进行了分析,得到如图12所示的啮合印痕图。从图中可以看出:当载荷为10 N·m时,齿面参与啮合的区域较小,齿面上半部分几乎不参与啮合;随着载荷增加到100 N·m,齿面参与啮合的区域逐渐增大;当载荷增加到一定范围之后,齿面参与啮合区域的变化逐渐减小,同时,载荷增加使齿面间的接触力增加。

(a)载荷为10 N·m

(b)载荷为100 N·m

(c)载荷为300 N·m

(d)载荷为500 N·m图12 载荷对啮合印痕及接触压力的影响

3.3 安装误差对啮合性能的影响

当中心距安装误差ΔE分别为-0.1、0和0.1 mm时,其对啮合印痕、角度传递误差和啮合刚度的影响规律如图13～图15所示。从图中可以看到:当存在中心距误差时,啮合印痕、角度传递误差均值和啮合刚度均值的变化都不大;负向中心距误差使角度传递误差峰峰值减小,正向中心距误差使角度传递误差峰峰值增大。

(a)中心距安装误差为-0.1 mm

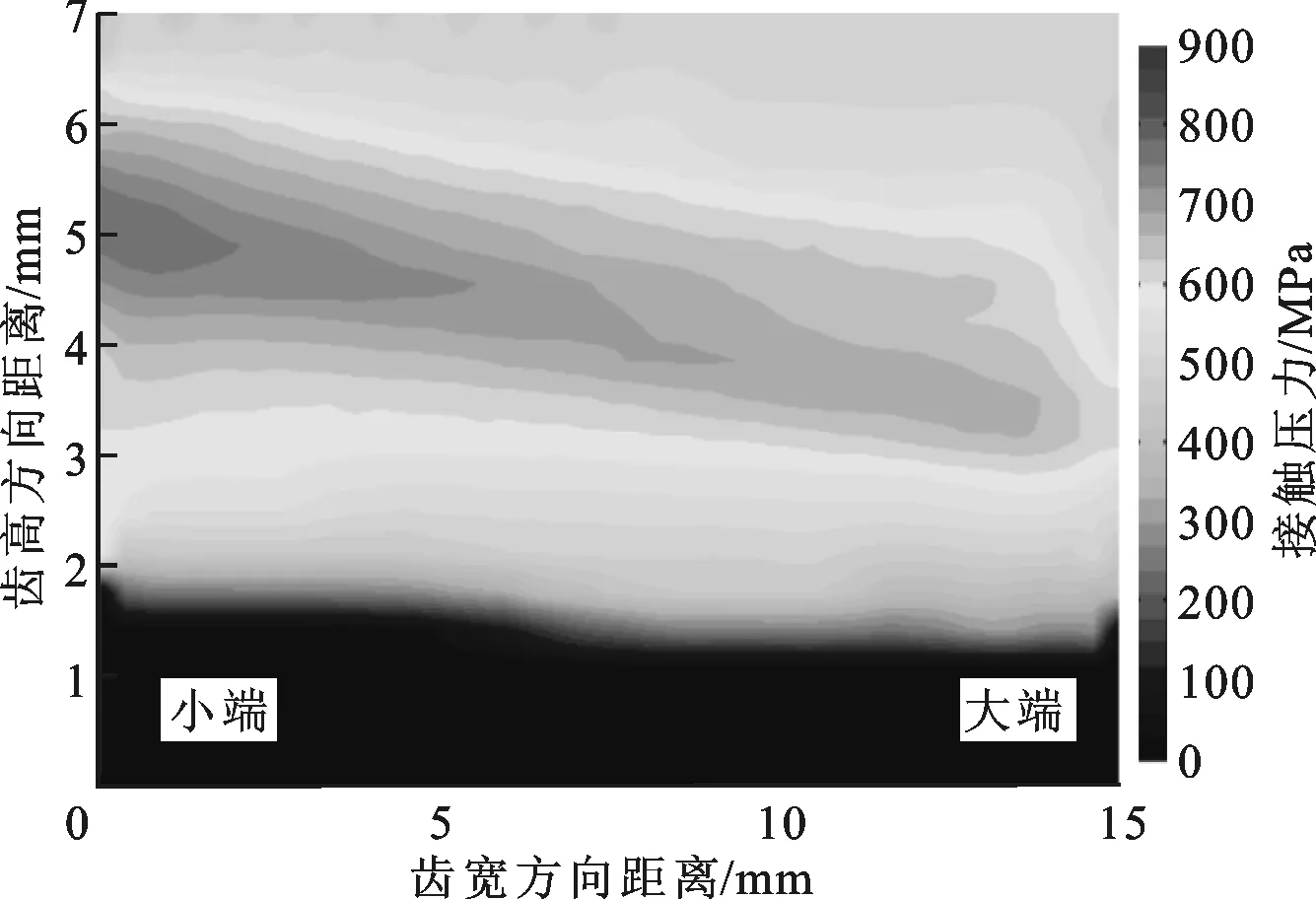
(b)中心距安装误差为0.1 mm图13 中心距安装误差对啮合印痕及接触压力的影响

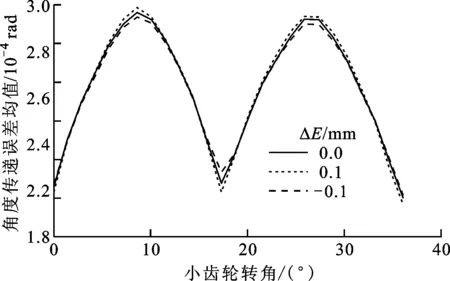
(a)对角度传递误差均值的影响

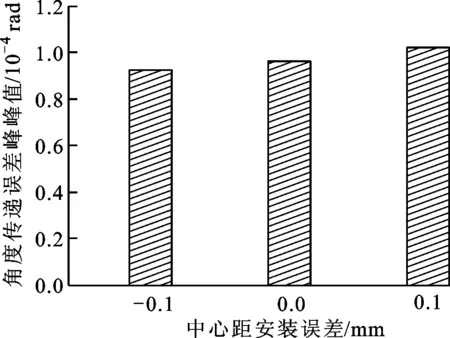
(b)对角度传递误差峰峰值的影响图14 中心距安装误差对角度传递误差及其峰峰值的影响

(a)对啮合刚度的影响

本文还分析了轴向位置安装误差和轴线平行度安装误差对啮合印痕、角度传递误差及啮合刚度的影响规律,结果表明:中心距误差和轴向位置误差对啮合印痕、角度传递误差及啮合刚度的影响较小;轴线平行度安装误差将导致齿轮副产生偏载,x方向的轴线平行度误差均使啮合刚度降低,x正向的轴线平行度误差使大齿轮的小端出现边缘接触,并使角度传递误差和均值和峰峰值均增大,导致传动精度降低;y方向的轴线平行度误差均使角度传递误差峰峰值增大,导致传动不平稳,y负向的轴线平行度误差使大齿轮的小端产生边缘接触,对于相同的轴线平行度误差量,y方向的轴线平行度误差对平行轴渐开线变厚齿轮副的啮合印痕影响更大。

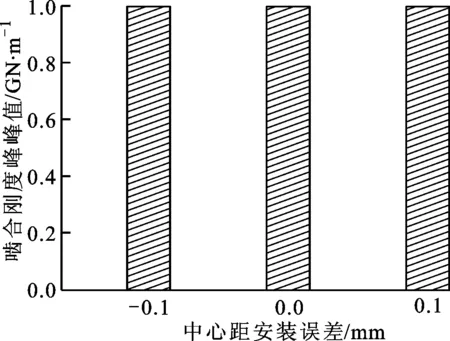
(b)对啮合刚度均值的影响图15 中心距安装误差对啮合刚度的影响

4 结 论

本文基于节圆锥共轭啮合理论,提出了平行轴渐开线变厚齿轮传动节圆锥模型,对平行轴渐开线变厚齿轮副进行了几何设计;研究了节锥角、载荷以及安装误差对角度传递误差、啮合刚度和啮合印痕的影响规律,得到的主要结论如下。

(1)节锥角的增大将导致齿面接触压力减小和齿轮副传动精度降低,但可使啮合刚度波动更为平缓,从而减小轮齿啮合过程中的内部时变激励,改善齿轮传动的啮合平稳性。

(2)随着载荷的增加,角度传递误差均值及峰峰值均增大,从而导致齿轮副传动精度降低,而啮合刚度变化不大,刚度波动趋于平缓。

(3)中心距安装误差和轴向位置误差对齿轮副的啮合特性影响不大,但轴线平行度误差将导致齿轮副产生边缘接触;齿轮副对x正向的轴线平行度误差和y负向的轴线平行度误差更为敏感;对于相同的轴线平行度误差量,y方向的轴线平行度误差所产生的边缘接触更加严重。

[1] TSAI S J, WU S H. Geometrical design of conical gear drives with profile-shifted transmission [C]∥Proceedings of 12th IFTOMM World Congress. Besancon, France: ASME, 2007: 18-21.

[2] WU S H, TSAI S J. Contact stress analysis of skew conical involute gear drives in approximate line contact [J]. Mechanism and Machine Theory, 2009, 44(9): 1658-1676.

[3] 李瑰贤, 吴俊飞, 李华敏, 等. 平行轴内啮合渐开线变厚齿轮的设计与计算 [J]. 中国机械工程, 2000, 11(8): 886-889. LI Guixian, WU Junfei, LI Huamin, et al. Design and calculation of internal beveloid gears with parallel axes [J]. China Mechanical Engineering, 2000, 11(8): 886-889.

[4] LI G X, WEN J M, ZHANG X, et al. Meshing theory and simulation of noninvolute beveloid gears [J]. Mechanism and Machine Theory, 2004, 39(8): 883-892.

[5] 林超, 魏沛堂, 朱才朝. 平行轴变齿厚斜齿轮传动接触分析 [J]. 重庆大学学报, 2012, 35(12): 1-6. LIN Chao, WEI Peitang, ZHU Caichao. Tooth contact analysis of helical beveloid gear with parallel axis [J]. Journal of Chongqing University, 2012, 35(12): 1-6.

[6] BRECHER C, BRUMM M, HENSER J. Validation of the tooth root load carrying capacity calculation of beveloid gears with parallel axes [C]∥VELEX P. Proceedings of International Gear Conference 2014. Lyon, France: Chandos Publishing, 2014: 1038-1048.

[7] ZHU Caichao, SONG Chaosheng, LIM T C, et al. Parametric analysis of gear mesh and dynamic response of loaded helical beveloid transmission with small shaft angle [J]. ASME Journal of Mechanical Design, 2012, 134(8): 90-99.

[8] ZHU Caichao, SONG Chaosheng, LIM T C, et al. Pitch cone design and influence of misalignments on tooth contact behaviors of crossed beveloid gears [J]. Mechanism and Machine Theory, 2013, 59(1): 48-64.

[9] 朱才朝, 刘立斌, 刘明勇, 等. 相交轴渐开线变厚齿轮几何设计与啮合特性分析 [J]. 机械工程学报, 2012, 48(23): 135-142. ZHU Caichao, LIU Libin, LIU Mingyong, et al. Geometry design and tooth contact analysis of intersected beveloid gears [J]. Journal of Mechanical Engineering, 2012, 48(23): 135-142.

[10]ZHU Caichao, LIU Libin, SONG Chaosheng, et al. Pitch cone design and tooth contact analysis of intersected beveloid gears for marine transmission [J]. Mechanism and Machine Theory, 2014, 82(12): 141-153.

[11]TRONG P D, PASCAL Z, PETER E. Simulation of contact forces and contact characteristics during meshing of elastic beveloid gears [J]. Computer Assisted Methods in Engineering and Science, 2014, 21: 91-111.

[12]LIU C C, TSAY C B. Tooth undercutting of beveloid gears [J]. Journal of Mechanical Design, 2001, 123(4): 569-576.

[13]LIU C C, TSAY C B. Contact characteristics of beveloid gears [J]. Mechanism and Machine Theory, 2002, 37(4): 333-350.

[14]LITVIN F L, Gear geometry and applied theory [M]. Cambridge, UK: Cambridge University Press, 2004: 375-403.

[15]贺敬良, 吴序堂. 交错轴锥形齿轮副几何设计的研究 [J]. 西安交通大学学报, 2003, 37(5): 471-474. HE Jingliang, WU Xutang. Study on geometric design of crossed-axes conical involute gears [J]. Journal of Xi’an Jiaotong University, 2003, 37(5): 471-474.

(编辑 葛赵青)

Geometric Design and Meshing Characteristics Analysis of Beveloid Gear Transmission with Parallel Axes

NI Gaoxiang,ZHU Caichao,SONG Chaosheng,LIU Huaiju

(State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China)

Based on spatial gearing theory, a pitch cone design model of beveloid gear transmission with parallel axes was developed, and the geometric design method of beveloid gear transmission with parallel axes was proposed. Considering the installation errors and deformation, a meshing model of beveloid gear transmission with parallel axes was developed to investigate the influences of the cone angle and load as well as installation errors on the meshing characteristics. The results show that the increasing of the cone angle can decrease the contact force and reduce the transmission precision of the gear pair, but suppress the fluctuation of meshing stiffness; the increasing of torque load can increase both the mean value and peak to peak value of transmission error, but has only small influence on the mean value of meshing stiffness. However, the installation error in axis parallelism has a strong effect on the meshing characteristics and it will cause edge contact in gear transmission. This edge contact caused by the axis parallelism installation error inydirection is more serious under the same error condition. The research results are expected to provide a theoretical basis for industrial popularization of the beveloid gear transmission with parallel axes.

beveloid gear; parallel axes; pitch cone design; meshing characteristics; installation error

10.7652/xjtuxb201605009

2015-09-22。 作者简介:倪高翔(1991—),男,博士生;朱才朝(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51405043,51575061,51175523);中国博士后科学基金资助项目(2015M582517)。

时间:2016-03-02

http:∥www.cnki.net/kcms/detail/61.1069.T.20160302.2014.008.html

TH132.413

A

0253-987X(2016)05-0057-08