多信号输入下多智能体系统的图可控性分类

李自强，纪志坚，晁永翠，董洁

(青岛大学 自动化工程学院，山东 青岛 266071)



多信号输入下多智能体系统的图可控性分类

李自强，纪志坚，晁永翠，董洁

(青岛大学 自动化工程学院，山东 青岛 266071)

在多信号输入情形下，对多智能体系统的图可控性分类进行了分析，构建了新的基于多信号输入下的系统模型。进而利用秩判据和PBH判据，在新的模型下得到系统与可控性的关系，新的模型更方便地表现多智能体系统的一般性。此外，在拉普拉斯矩阵下，对多智能体系统与可控性的关系做了详细的分析与研究，特别是在拉普拉斯矩阵的特征值与系统能控性的关系方面进行了分析。解决了多信号输入下可控性分类的问题，并提高了研究可控性的准确性。而且，在已有结论的基础上对多智能体系统可控性的内容进行了完善。

多信号输入系统；图可控性分类；秩判据和PBH判据；拉普拉斯矩阵；可控性

近几年来学术界对多智能体系统已经有了广泛的研究和关注[1-14]，并且已经应用在多个领域中，如无人机的编队控制、机器人的编队控制，甚至在军事上也有广泛的应用[15-17]。多智能体系统的核心问题是关于可控性的问题，可控性能够使每个智能体的状态达到人们所期望的结果，并且使多智能体系统发挥最大的作用。所以，多智能体系统的可控性研究具有重要的意义。

在多智能体系统中，对具有领导者—跟随者结构的图可控性研究大都是基于单信号输入下或者是更为简单的模型下[13,18]，在多智能体中，模型的建立对系统的可控性有着重要的影响。在所建立的模型下，充分认识系统与可控性的关系，并理解系统对可控性的影响，这些无疑对解决多智能体系统的可控性问题提供了很好的方法和帮助。所以研究特定模型下系统的可控性成为一个热点。

Tanner是最早通过系统中各节点之间的联系来研究可控性的[19]。他通过邻居信息，提出了其中一个节点为领导者时系统可控的充分必要条件，并得到了无向图下的能控性定理。这对后续有关可控性的研究给予了很大的帮助。早在Aguilar的文章中[18]，Aguilar就整个图的可控性进行分类，根据图选取不同的领导者时图是否可控，来定义了3种图可控性，并就3种分类进行了详细的分析，但是Aguilar的文章内容是在单信号输入的特殊模型下进行研究的，即每个领导者节点受到同一个信号的输入，而本文是在更一般的多信号输入模型下进行研究，每个领导者节点可能受到不同的多个信号的输入，这种多信号输入的模型更能准确地表现多智能体系统的一般性，而且本文纠正了Aguilar文章[18]中关于齐次向量的条件可控图问题。

一些研究者[19-22]近几年对基于拉普拉斯矩阵下的可控性作了很多的研究，本文也是在拉普拉斯矩阵下，结合矩阵论的知识[23-25]，对系统的可控性与拉普拉斯矩阵的关系进行了研究，特别是在拉普拉斯矩阵的特征值和特征向量等对系统可控性的影响方面进行了深入的研究，另外，本文主要在多输入信号情况下，对多智能体系统中的图可控性进行分类，具体分为多信号输入下本质可控图，多信号输入下完全不可控图以及多信号输入下条件可控图，并就这3种分类的特殊性进行了描述，而且对它们的性质进行了相应的阐述。

1 预备知识

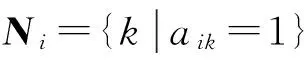
在图G中，对于点集合的两个节点i和节点j，定义节点i和节点j之间的距离为dG(i,j)，表示为节点i和节点j之间最短的通道。当图中任意一对节点之间存在一条通道时，我们说图G是连通的。拉普拉斯矩阵是半正定且实对称的，因此L的特征值可以给定顺序为λ1≤λ2≤…≤λn，其中特征值λ1=0对应的特征向量为[1 1 … 1]T。如果图G是连通的，则λ1=0是L的非重特征根，此时有λ2>0，本文中图G的特征值或特征向量即为图拉普拉斯矩阵L的特征值或特征向量。

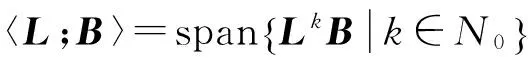
本文主要分析G=(V,E)上的可控性问题，其中xi(t)∈R代表了节点i∈V在时刻t时的状态，节点间的相互关系由边集E来表示。在时刻t时，一个外部控制向量通过一状态向量bm∈Rq施加在节点i上。单个节点的状态方程可以表示为

另外，在时刻t，输出方程y(t)∈Rp由输出矩阵C∈Rn×p表示。所以对于连通图G=(V,E)，整个系统方程表示为

式中B=[b1b2…bn]T∈Rn×q。

定义1 如果所有领导者节点都受到同一个信号的输入，那称这样的系统为单信号输入系统。当系统受到多个信号输入时，称这样的系统为多信号输入系统。

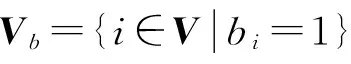
另一种情况是在n个点的图中，定义输入节点集合S，每个点可能收到多个信号的输入，相应的输入矩阵为

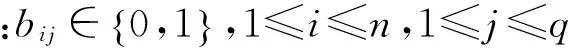
2 主要结论

首先讨论单信号输入下系统可控性与多信号输入下系统可控性的区别和联系。

多信号输入下系统可控性与单信号输入下系统可控性是有很大区别的，在选取的领导者下，有些图在单信号输入系统下是不可控的，但在多信号输入系统下却不一定不可控。

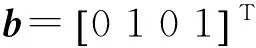
图1 具有4个节点的图

当任意选取领导者节点时，有些图在单信号输入系统下是完全不可控的，但在多信号输入系统下并非完全不可控的。

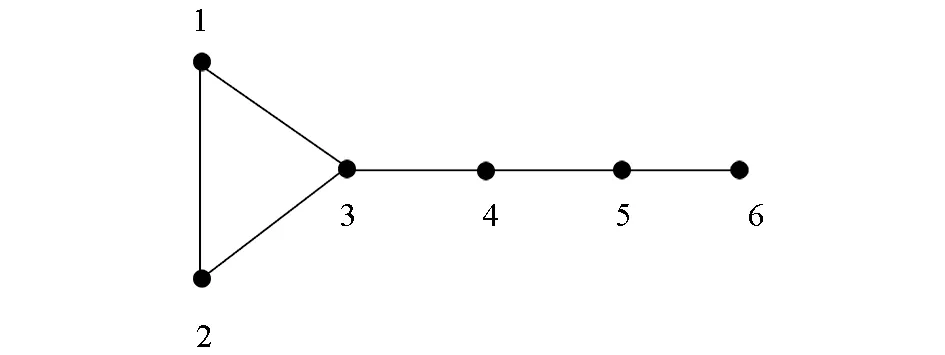
图2 具有6个节点的图

通过上文，可以看出多信号输入下可控性与单信号输入下可控性有很大的区别，那么就有必要讨论基于拉普拉斯矩阵下的多信号输入系统与系统可控性的关系，本文通过下面的定理给出。

定理 1假定可对角化矩阵L无重特征值，矩阵U是由L的线性无关的单位特征向量构成的矩阵，那么〈L;B〉的维数等于W=U-1B中非零列向量的个数。特别地，系统(L,B)是可控的充要条件是W矩阵中无零列向量。当L有重特征值，且wi≠0q时，系统(L,B)是不可控的，当且仅当重特征值λi所对应的向量组wi中，存在线性相关的向量，其中i=1,2，…,n。

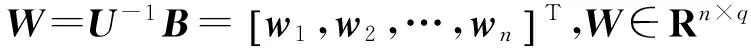
由于U是非奇异矩阵，所以它不影响式(3)右边矩阵的秩，右边的矩阵展开后即为

对上式进行列变换得

(4)

当特征值不同时，式(4)后面的矩阵是满秩的，只需考虑式(4)前面1×q矩阵，其中每个元素为n×n的对角矩阵，则此矩阵实际上是具有n行，n×q列的矩阵:

当L有重特征值情况时，根据无重特征值的情况，证明如下：

通过下面情况的论述都能够验证定理1中无重特征值时的情况。对于具有个n个节点的图，节点2和节点4为领导者节点时，此时W=U-1B=

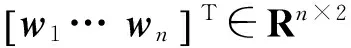
在L无重特征值下，仅当存在wi2=wi4=0时，〈L;B〉的维数小于n，〈L;B〉的维数等于wi中非零向量的个数。而且当且仅当wi≠0时，dim(〈L;B〉)=n，即此时系统可控。

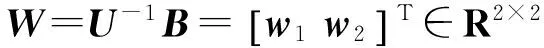
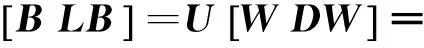
由于U是非奇异矩阵，所以它不影响式(5)右边矩阵的秩，对式(5)右边矩阵进行列变换得

在λ1≠λ2下，上式后面的矩阵是满秩的，根据前面的矩阵，只有当w11=w12=0或w21=w22=0时，〈L;B〉的维数小于2，而且当且仅当wi≠0时，dim(〈L;B〉)=2，即此时系统可控。

令En为n×q维的矩阵，并且矩阵中的每个元素为1;0n为n×q维的矩阵，并且矩阵中的每个元素为0;1n为n维列向量，且每个元素都为1;0q为q维列向量，且每个元素都为0。下面推论由定理1的证明可得。

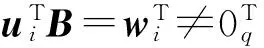
注释单信号输入系统下，对应的拉普拉斯矩阵如果存在重特征值，则系统不可控；但是在多信号输入系统下，并不能单纯依靠存在重特征值来判断系统的不可控性。

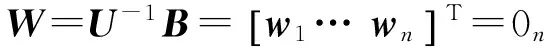
证明同理定理1证明为

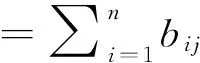
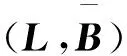
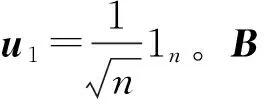
即

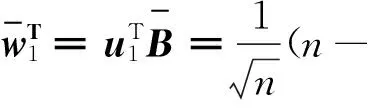
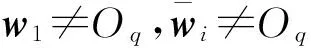
通过上文的阐述，可以给出多信号输入下图可控性分类的定义。

定义2在连通图G中，对于系统(1)

1)如果除去图中每个点都是输入节点以及每个点都不是输入节点的2种情况后，任意选取图中的点为输入节点时，系统(L,B)是可控的，则图关于B是多信号输入下本质可控图；

2)如果在图中选取任意点为输入节点时，系统(L,B)都是不可控的，则图关于B是多信号输入下完全不可控图；

3)如果图关于B即不是多信号输入下本质可控图也不是多信号输入下完全不可控图，则图关于B是多信号输入下条件可控图。

下面是分情况讨论3种情况下的图性质。

2.1 多信号输入下本质可控图

在本节中，主要给出2个多输入下本质可控图的必要条件，通过下面的命题论证。

命题1多输入下本质可控图是不对称的。

证明设G是多输入下本质可控图，则L必须有不同的特征值。在这用反证法，假设多输入下本质可控图是对称的，则G有一个非平凡自同构群，设J是置换矩阵代表G的一个非恒等自同构，那么存在2个不同的标准正交基ei和ej，使得Jei=ej和Jej=ei。则有J[ei0n…]=[ej0n…]和J[0nej…] = [0nei…]。并且有JL(G)=L(G)J，令B=[ei0n…]+[0nej…]。可以得到JB=B。设λ为矩阵L的特征值，其对应的特征向量为v，满足Lv=λv。两边同乘以J，有JLv=Jλv，因为JL(G)=L(G)J，则有L(Jv)=λ(Jv)，即Jv也是对应于特征值λ的特征向量。因为L有一系列正交特征向量，v-Jv也是L的特征向量。而且JB=JTB=B，则有(v-Jv)TB=vTB-vTJTB=vTB-vTB=0即B正交于L的特征向量。因此系统(L,B)是不可控的。这与G是多输入下本质可控图相矛盾。所以多输入下本质可控图是不对称的。结论得证。

任何少于6个点的图都可以改为对称的图。如图3(a)中，5个点的情况可以改为图3(b)中对称的图形。由此启发可以得到下面的命题。

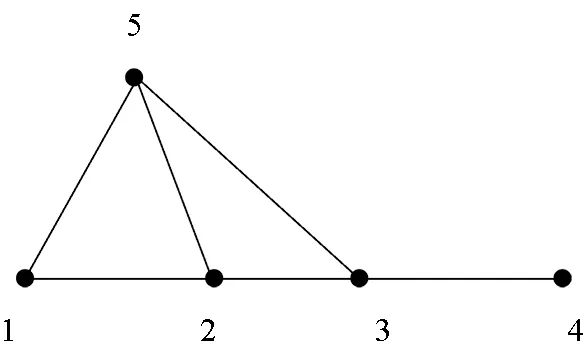
(a)改变前

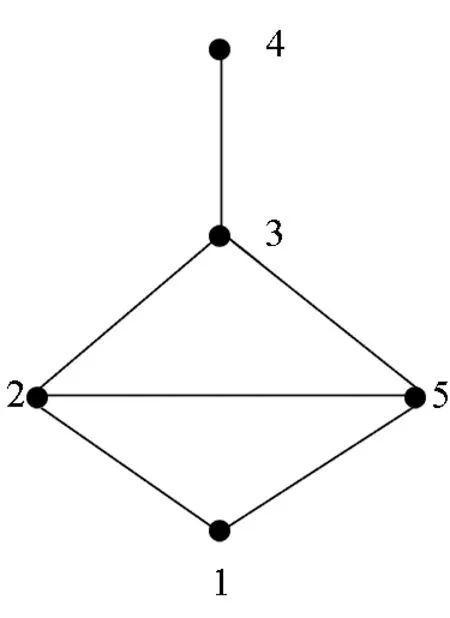
(b)改变后

命题 2多输入下本质可控图至少有6个点。

证明根据命题1，并且由任何不对称的图形至少有6个点得证。

对于系统(1)，不对称的图并不都是多输入下本质可控图。通过图(4)可以进行验证。

图4 具有6个节点的不对称图

图4是一个在给定点标记下的不对称图，它的拉普拉斯矩阵为

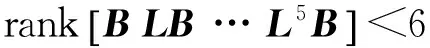
2.2 多信号输入下完全不可控图

相对于多信号输入下本质可控图，图对称与否并不与多信号输入下完全不可控图有关联。对于系统(1)，对称的图并不都是多输入下完全不可控图。如图1为对称图，当B=[e2e4]时，根据秩判据，此时系统可控。

给定图G，则可以写出图的拉普拉斯矩阵，也可以求出图的特征值，特征值所对应的特征向量也可以求出，由此启发，给出下面的命题。

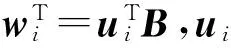
证明根据定理1，得证。

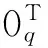
证明根据定理1，得证。

2.3 多信号输入下条件可控图

在本节中，主要提出文献[18]中的错误，并举例进行阐述。

对于文献[18]中的模型(2)实际上是系统(1)的特殊情况，即单信号输入系统，此时要在系统(2)下进行分析与讨论文献[18]中的问题。

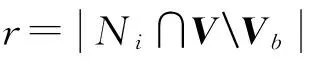
对于文献[18]中推论4.2：G是一个含有n个点的连通图，并且n≥3时，如果G有一个(r,s)-齐次可控向量，则G是条件可控的。

如图5，在系统(2)下，令b=[0 0 1 1 0 0]T，其中i∈Vb={3,4}，若i=3，则Ni={1,2}且j∈VVb={1,2,5,6}，得r=2，即领导节点3与2个跟随者邻接，若j=1，则Nj={3}，得s=1，即跟随者节点1与1个领导者邻接。由此称b=[0 0 1 1 0 0]T在图G中是一个(2,1)-齐次可控向量。则根据文献[18]中推论4.2得图G是条件可控的。

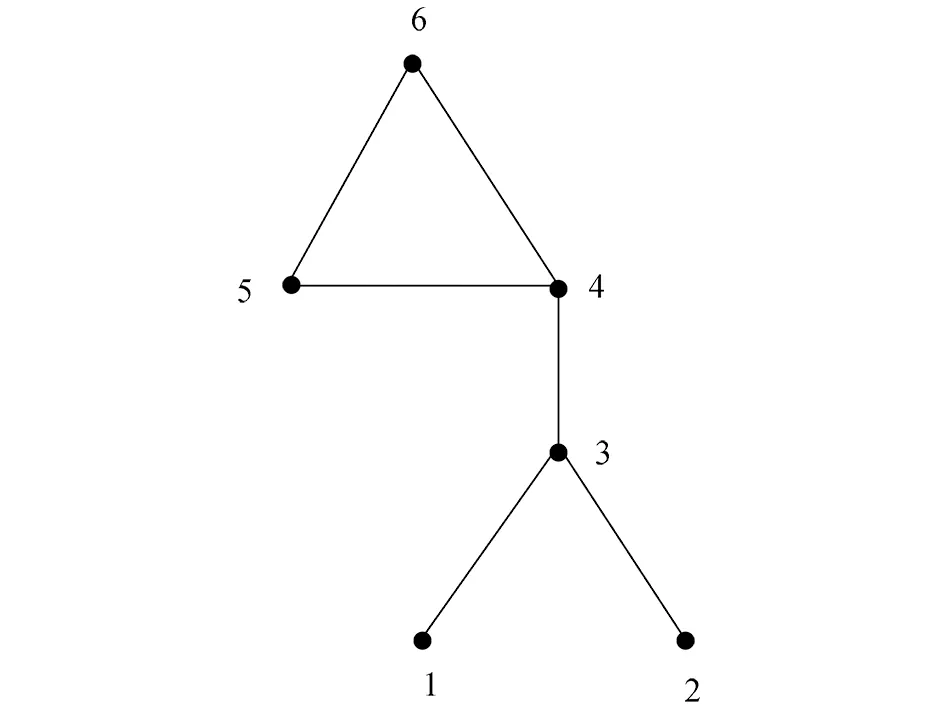
图5 具有6个节点的对称图

图5的拉普拉斯矩阵为

可以求出它有一个两重的特征值为3。即图5具有重特征值，根据注释，在单信号输入系统下可以得到图G是完全不可控的，显然是矛盾的，所以文献[18]中推论4.2是错误的。在多信号输入系统下，更不能通过齐次向量来判断图的条件可控性。

3 结束语

本文就多信号输入系统下的可控性分类问题进行了详细的研究与分析，并对拉普拉斯矩阵下特征值和特征向量与可控性的关系进行了阐述和论证，论述了单信号输入系统与多信号输入系统的区别和联系，而且纠正了文献[18]中关于齐次可控向量应用在条件可控图上的错误。本文对可控性分类的研究方法和结果，为以后研究更复杂的图可控性问题提供了方向和帮助。

[1]OLFATI-SABER R, MURRAY R M. Consensus problems in networks of agents with switching topology and time-delays[J]. IEEE transactions on automatic control, 2004, 49(9): 1520-1533.

[2]JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE transactions on automatic control, 2003, 48(6): 988-1001.

[3]JI Z J, LIN H, LEE T H. Controllability of multi-agent systems with switching topology[C]//Proceeding of the 2008 IEEE Conference on Robotics, Automation and Mechatronics. Chengdu: IEEE, 2008: 421-426.

[4]刘菲, 纪志坚. 时滞二阶离散多智能体系统的可控性[J]. 系统科学与数学, 2015(3): 298-307. LIU Fei, JI Zhijian. Controllability of second-order discrete-time multi-agent systems with time-delay[J]. Journal of systems science and mathematical sciences, 2015(3): 298-307.

[5]董洁, 纪志坚, 王晓晓. 多智能体网络系统的能控性代数条件[J]. 智能系统学报, 2015, 10(5): 747-754. DONG Jie, JI Zhijian, WANG Xiaoxiao. Algebraic conditions for the controllability of multi-agent systems[J]. CAAI transactions on intelligent systems, 2015, 10(5): 747-754.

[6]晁永翠, 纪志坚, 王耀威, 等. 复杂网络在路形拓扑结构下可控的充要条件[J]. 智能系统学报, 2015, 10(4): 577-582. CHAO Yongcui, JI Zhijian, WANG Yaowei, et al. Necessary and sufficient conditions for the controllability of complex networks with path topology[J]. CAAI transactions on intelligent systems, 2015, 10(4): 577-582.

[7]王晓晓, 纪志坚. 广播信号下非一致多智能体系统的能控性[J]. 智能系统学报, 2014, 9(4): 401-406. WANG Xioaxiao, JI Zhijian. Controllability of non-identical multi-agent systems under a broadcasting control signal[J]. CAAI transactions on intelligent systems, 2014, 9(4): 401-406.

[8]JI M, EGERSTEDT M. A graph-theoretic characterization of controllability for multi-agent systems[C]//Proceeding of the American Control Conference, 2007. New York: IEEE, 2007: 4588-4593.

[9]JIANG Fangcui, WANG Long, XIE Guangming, et al. On the controllability of multiple dynamic agents with fixed topology[C]//Proceeding of the American Control Conference, 2009. St. Louis, Missouri, USA: IEEE, 2009: 5665-5670.

[10]JI Zhijian, WANG Zidong, LIN Hai, et al. Controllability of multi-agent systems with time-delay in state and switching topology[J]. International journal of control, 2010, 83(2): 371-386.

[11]LIU Bo, CHU Tianguang, WANG Long, et al. Controllability of a leader-follower dynamic network with switching topology[J]. IEEE transactions on automatic control, 2008, 53(4): 1009-1013.

[12]RAHMANI A, JI Meng, MESBAHI M, et al. Controllability of multi-agent systems from a graph-theoretic perspective[J]. SIAM journal on control and optimization, 2009, 48(1): 162-186.

[13]MARTINI S, EGERSTEDT M, BICCHI A. Controllability analysis of multi-agent systems using relaxed equitable partitions[J]. International journal of systems, control and communications, 2010, 2(1/2/3): 100-121.

[14]CHAPMAN A, MESBAHI M. On symmetry and controllability of multi-agent systems[C]//Proceeding of the 2014 IEEE 53rd Annual Conference on Decision and Control. Los Angeles, CA, USA: IEEE, 2014: 625-630.

[15]刘金琨, 尔联洁. 多智能体技术应用综述[J]. 控制与决策, 2001, 16(2): 133-140, 180. LIU Jinkun, ER Lianjie. Overview of application of multiagent technology[J]. Control and decision, 2001, 16(2): 133-140, 180.

[16]朱战霞, 郑莉莉. 无人机编队飞行控制器设计[J]. 飞行力学, 2007, 25(4): 22-24. ZHU Zhanxia, ZHENG Lili. The controller design of UAV formation flight[J]. Flight dynamics, 2007, 25(4): 22-24.

[17]LANE D M, MCFADZEAN A G. Distributed problem solving and real-time mechanisms in robot architectures[J]. Engineering applications of artificial intelligence, 1994, 7(2): 105-117.

[18]AGUILAR C O, GHARESIFARD B. Graph controllability classes for the laplacian leader-follower dynamics[J]. IEEE transactions on automatic control, 2014, 60(6): 1611-1623.

[19]TANNER H G. On the controllability of nearest neighbor interconnections[C]//Proceeding of the 43rd IEEE Conference on Decision and Control. Nassau, Bahamas: IEEE, 2004: 2467-2472.

[20]HONG Yiguang, GAO Lixin, CHENG Daizhan, et al. Lyapunov-based approach to multiagent systems with switching jointly connected interconnection[J]. IEEE transactions on automatic control, 2007, 52(5): 943-948.

[21]MOREAU L. Stability of multiagent systems with time-dependent communication links[J]. IEEE transactions on automatic control, 2005, 50(2): 169-182.

[22]OGREN P, EGERSTEDT M, HU Xiaoming. A control Lyapunov function approach to multiagent coordination[C]//Proceedings of the 40th IEEE Conference on Decision and Control. Orlando, Florida, USA: IEEE, 2001: 1150-1155.

[23]BIGGS N. Algebraic graph theory[M]. 2nd ed. Cambridge: Cambridge University Press, 1993.

[24]王树禾. 图论[M]. 北京: 科学出版社, 2004.

[25]CHARTRAND G, ZHANG Ping. 图论导引[M]. 范益政, 译. 北京: 人民邮电出版社, 2007: 1-17. CHARTRAND G, ZHANG Ping. Introduction to graph theory[M]. FAN Yizheng, trans. Beijing: The People's Posts and Telecommunications Press, 2007: 1-17.

李自强，男，1991年生，硕士研究生，主要研究方向为多智能体系统。

纪志坚，男，1973年生，博士，教授，博士生导师，主要研究方向为群体系统动力学与协调控制、复杂网络、切换动力系统的分析与控制、系统生物以及基于网络的控制系统等。曾主持国家自然科学基金3项、山东省杰出青年科学基金项目1项。山东省杰出青年基金获得者，发表学术论文70余篇，其中被SCI检索23篇，EI 检索50余篇。

晁永翠，女，1990年生，硕士研究生，主要研究方向为复杂网络的可控性。

Graph controllability classes of networked multi-agent systems with multi-signal inputs

LI Ziqiang， JI Zhijian， CHAO Yongcui， DONG Jie

(School of Automation Engineering，Qingdao University, Qingdao 266071，China)

In this paper, we analyze graph controllability classes in networked multi-agent systems with multisignal inputs and construct a new system model. To determine the relationship between controllability and networked multi-agent systems, we used a controllability rank criterion and the Popov-Belevitch-Hautus criterion in our proposed model, which is more convenient and more general in its application. In addition, we analyzed in detail the relationship between networked multi-agent systems and controllability, especially, between Laplacian eigenvalue and controllability. Based on our results, we conclude that we have solved the controllable classification problem associated with multisignal input, improved research accuracy with respect to controllability, and improved the controllability of networked multi-agent systems.

multi-signal input systems; graph controllability classes; rank criterion and PBH criterion; Laplacian matrix; controllability

2016-01-08.

日期：2016-09-13.

国家自然科学基金项目(61374062)；山东省杰出青年科学基金项目(JQ201419).

纪志坚.E-mail：jizhijian@pku.org.cn.

TP273

A

1673-4785(2016)05-0680-08

10.11992/tis.201601017

http://www.cnki.net/kcms/detail/23.1538.TP.20160913.0838.002.html

李自强，纪志坚，晁永翠，等.多信号输入下多智能体系统的图可控性分类[J]. 智能系统学报， 2016, 11(5):680-687.

英文引用格式：LI Ziqiang，JI Zhijian，CHAO Yongcui，et al.Graph controllability classes of networked multi-agent systems with multi-signal inputs[J]. CAAI transactions on intelligent systems, 2016,11(5):680-687.