基于自由矩阵不等式方法的中立型时滞系统稳定判据
2016-12-23练红海肖伸平陈海东
练红海,肖伸平,陈 刚,陈海东
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
基于自由矩阵不等式方法的中立型时滞系统稳定判据
练红海,肖伸平,陈 刚,陈海东
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
针对一类不确定中立型时滞系统的鲁棒稳定性问题,采用自由矩阵积分不等式(FMBII)方法进行深入研究。提出了一种简化的FMBII,利用它估计Lyapunov-Krasovskii泛函的导数,得到具有更低保守性的时滞相关稳定判据。最后,通过2个数值实例,将本文方法与文献[4], [5], [7], [8]所提方法进行比较。数值实例结果表明了本文方法的有效性和优越性。
自由矩阵积分不等式;中立型时滞系统;稳定性
0 引言
在实际应用系统中,许多系统的数学模型都是利用时滞状态和时滞状态的导数,通过中立型泛函微分方程来描述,例如:无损传输线、微波振荡器、汽水管道的动态处理以及分布网络等[1]。时滞在系统中频繁出现,常常引起系统不稳定并产生振荡[2-5]。因此,国内外学者针对不同类型中立型时滞系统(neutral delay systems,NDS)的稳定性问题进行了讨论和研究,并取得了大量的研究成果[2-8]。
中立型时滞系统的稳定性分析主要有2类方法:直接的Lyapunov方法和输入-输出方法,而直接的Lyapunov方法在分析系统的稳定性问题时,更加简单有效。针对时变NDS,文献[2]和文献[3]利用增广Lyapunov-Krasovskii泛函方法,获得了相应的稳定条件。文献[5]利用自由权矩阵方法研究了NDS鲁棒稳定和镇定,文献[6]也提出了该方法。文献[8]利用时滞分割方法,使其泛函包含更多的信息,得到了具有较低保守性的NDS稳定准则,此方法由于将时滞分成了若干个区间,泛函也分成了若干段,增加了推导的复杂性和计算的运行时间。要获得保守性小的稳定条件主要从2方面入手:一是选择合适的泛函;二是对其泛函导数进行严格约束。因此,许多学者提出了不同的积分不等式约束泛函导数的积分项,如Jense、Wirtinger积分不等式等。Zeng Hongbing等在文献[9]和[10]提出了2类不同的自由矩阵积分不等式(free-matrix-based integral inequality,FMBII)。
本文在文献[10]提出的FMBII基础上,对其做了简化,提出了一种简化的FMBII。利用FMBII约束Lyapunov-Krasovskii泛函导数中的积分项,获得NDS的鲁棒时滞相关稳定判据。最后,2个数值实例表明了本文提出的方法具有更低的保守性,相比已有结果更有优越性。
本文采用如下标号。
Rn和Rn×m分别代表实数域的n维向量空间和n×m的矩阵空间;
X-1和XT分别代表矩阵的逆和转置;
0和I分别表示合适维数的零矩阵和单位矩阵;
Sym{Y}=Y+YT表示矩阵Y与其转置之和;
“*”表示矩阵中的对称项。
1 系统描述



2 主要结果



3 数值算例
例1 考虑标称NDS式(4)具有如下矩阵参数:

对不同的c,由定理1、文献[4]和[5]中的稳定判据,得到最大时滞上界h如表1所示。从表1可知,定理1所得最大时滞上界与文献[4],[5]相比,具有一定的优越性。

表1 不同c下的最大时滞上界hTable 1 Maximum upper bounds of h with c the variable
注3 文献[5]提出的自由权矩阵方法,在推导时滞相关条件方面被视为一种有效方法。这个数值实例表明本文提出的方法优于文献[5]。
例2 考虑具有结构不确定性的NDS式(1)具有如下矩阵参数:

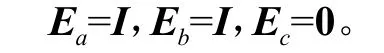
对不同的 ,由定理1、文献[7]和[8]中的稳定判据得最大时滞上界h如表2所示。从表2可知,本文提出的方法比文献[8]使用的时滞分段方法(分段数甚至达到q=5)和文献[7]使用的广义系统方法,具有更低的保守性。

表2 不同 下的最大时滞上界hTable 2 Maximum upper bounds of h with the variable
注4 时滞分段方法被广泛用于推导具有保守性小的时滞相关条件,时滞分段的数量越多,得到条件的保守性越小。但时滞分段的数量直接影响所得线性矩阵不等式的维度,分割数量越大,矩阵维数也越大,计算负担也急剧增加。
4 结论
本文提出了一种简化的FMBII,并利用提出的FMBII进一步研究NDS的稳定性问题。先构造一个合适的增广Lyapunov-Krasovskii泛函,并利用简化的FMBII估计其导数的积分项,得到2个新的NDS时滞相关稳定条件。最后,通过数值算例展示了本方法的可行性和优越性。简化的FMBII能应用到其他时滞系统,例如:神经网络、基因调控网络、模糊控制系统以及电力系统等。
[1]SAKTHIVEL R,MATHIYALAGAN K,MARSHAL ANTHONI S. Robust Stability and Control for Uncertain Neutral Time Delay Systems[J]. International Journal of Control,2012,85(4):373-383.
[2]肖伸平,曾红兵. 中立型时变时滞系统时滞相关稳定性[J]. 湖南工业大学学报,2009,23(4):58-61. XIAO Shenping,ZENG Hongbing. On Delay-Dependent Stability of Neutral Systems with Time-Varying Delay[J]. Journal of Hunan University of Technology,2009,23(4):58-61.
[3]白 雷,肖伸平,曾红兵,等. 中立型变时滞系统鲁棒稳定性分析[J]. 湖南工业大学学报,2012,26(1):50-54.
BAI Lei,XIAO Shenping,ZENG Hongbing,et al. Analysis on Robust Stability of Neutral Systems with Time-Varying Delay[J]. Journal of Hunan University of Technology,2012,26(1):50-54.
[4]HAN Qinglong. Robust Stability of Uncertain Delay-Differ-Ential Systems of Neutral Type[J]. Automatica,2002,38 (4):719-723.
[5]WU Min,HE Yong,SHE Jinhua. New Delay-Dependent Stability Criteria and Stabilizing Method for Neutral Systems [J]. IEEE Transactions on Automatic Control,2005,49 (12):2266-2271.
[6]HE Yong,WU Min,SHE Jinhua,et al. Delay-Dependent Robust Stability Criteria for Uncertain Neutral Systems with Mixed Delays[J]. Systems & Control Letters,2004,51 (1):57-65.
[7]YUE Dong,HAN Qinglong. A Delays-Dependent Stability Criterion of Neutral Systems and Its Application to a Partial Element Equivalent Circuit Model[C]// IEEE Transactions on Circuits and Systems II:Express Briefs. [S. l.]:IEEE, 2004,6(12):5438-5442.
[8]ZHANG Xianming,HAN Qinglong. A New Stability Criterion for a Partial Element Equivalent Circuit Model of Neutral Type[J]. IEEE Transactions on Circuits and Systems II:Express Briefs,2009,56(10):798-802.
[9]ZENG Hongbing,HE Yong,WU Min,et al. Free-Matrix-Based Integral Inequality for Stability Analysis of Systems with Time-Varying Delay[J]. IEEE Transactions on Automatic Control,2015,60(10):2768-2772.
[10]ZENG Hongbing,HE Yong,WU Min,et al. New Results on Stability Analysis for Systems with Discrete Distributed Delay[J]. Automatica,2015,60(C):189-192.
[11]SEURET A,GOUAISBAUT F. Wirtinger-Based Integral Inequality:Application to Time-Delay Systems[J]. Automatica,2013,49(9):2860-2866.
(责任编辑:邓 彬)
Stability Criteria for Neutral Delay Systems Based on Free Matrix Inequalities
LIAN Honghai,XIAO Shenping,CHEN Gang,CHEN Haidong
(School of Electrical and Information Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
In view of the robust stability exhibited by an uncertain neutral system with time delays, an intensive research has thus been conducted by adopting the free-matrix-based integral inequality (FMBII) method. A simplified FMBII is proposed for the estimation of the derivative of Lyapunov- Krasovskii functional, thus obtaining the delaydependent stability criteria with less degree of conservation. Finally, a comparison has been made between the current proposed method and the existing methods (see [4], [5], [7]and[8]), with the numerical example results verifying the validity and superiority of the currenth proposed approach.
free-matrix-based integral inequality;neutral delay systems;stability
TP13
A
1673-9833(2016)05-0037-04
10.3969/j.issn.1673-9833.2016.05.008
2016-07-25
国家自然科学基金资助项目(61304064),国家火炬计划基金资助项目(2015GH712901),湖南省自然科学基金资助项目(2015JJ3064),湖南省教育厅科学研究优秀青年基金资助项目(15B067),广东省特种光纤材料与器件工程技术研究开发中心开放基金资助项目
练红海(1990-),男,湖南永州人,湖南工业大学硕士生,主要研究方向为鲁棒控制,神经网络,时滞系统,E-mail:1132830550@qq.com
肖伸平(1965-),男,湖南永州人,湖南工业大学教授,主要从事鲁棒控制,过程控制,时滞系统等方面的教学与研究,E-mail:xsph_519@163.com
