轴承滚珠面型误差激光干涉测量系统的研究

郝维娜,令锋超,刘志刚,洪军,朱永生

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)



轴承滚珠面型误差激光干涉测量系统的研究

郝维娜,令锋超,刘志刚,洪军,朱永生

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

在以激光干涉方法进行轴承滚珠面型误差测量时,为避免特制参考标准球面镜自身球度误差对测量结果的影响,提出了一种以平面镜代替球面镜的泰曼-格林轴承滚珠面形误差干涉测量方法,并设计了相应的测量系统。该方法基于相移干涉原理,通过计算机控制压电晶体使参考平面镜获得固定步数的位移,以获得多幅干涉图像,使用电荷耦合图像传感器(CCD)对得到的干涉图像进行采集,系统对获取图像进行相位提取解包裹运算以得到球面的面型误差。对于测量中由轴承滚珠定位精度而引起的离焦、倾焦调整误差,采用泽尼克多项式波面拟合的方法来消除其对测量结果的影响。实验表明,该系统的测量结果与ZYGO干涉仪所得到的结果相比较,峰峰值相差0.001 6λ,均方根误差相差0.004λ,能够有效地对轴承滚珠面型进行检测,且测量结果具有较高的可靠性。此外,该方法还可进一步推广应用于其他需要进行圆球度测量的领域,具有广泛应用前景。

相移干涉;轴承滚珠;波面拟合;调整误差

滚动轴承在精密机械系统中具有广泛的应用,如作为航空发动机转子系统支撑部件、高速铁路车辆支撑部件、机床主轴重要组件等。滚珠作为滚动轴承的核心元件,承担着减小摩擦、承载负载的作用,高精度的轴承滚珠可以增加轴承使用寿命,提高轴承旋转精度。在滚珠的生产过程中,往往会存在一定的加工误差,导致生产滚珠的精度难以得到有效的保障,从而影响到整个轴承的寿命。因此,研究高精度、高效率滚珠检测方法对轴承的加工制造具有重要的应用价值。

轴承滚珠面型误差测量实质就是其球度测量。球度的精密测量方法[1]主要有三坐标测量法、圆度仪测量法和光学干涉测量方法。三坐标测量法是通过机械接触式探针来逐点获取物体表面的三维坐标,其机械结构复杂、测量范围受机械装置大小限制、测量效率低。圆度仪测量法是通过回转轴法测量工件的圆度误差,可以在一定程度上进行球面面型误差测量,但其测量精度有限。以上两种方法是典型的接触式测量,测量时容易对被测件表面造成二次损伤,难以满足高精度测量的要求。光学干涉测量法[2]是一种高精度、高灵敏度的快速非接触计量测试方法,它以光的波长为计量单位,测量效率高、精度高且对被测件无损伤。球面误差的干涉测量方法[3-4]是以双光束干涉为基本依据,由干涉系统标准镜反射的标准波面(理想波面)与球面反射的待检波面(包含面型误差信息)相干涉,从干涉图像提取相位信息,求解出待测球面面型误差。典型的干涉测量仪器是美国ZYGO公司推出的一款基于斐索干涉光路[5-7]的测量仪,为不同的测量任务而设计,包括平面和球面表面面型的非接触式测量。虽然传统干涉测量系统可以高精度测量球面面型误差,但其参考标准镜使用特制标准球面镜,加工制造复杂,造成测量成本较高,且系统测量精度往往受制于标准球面镜的精度。

传统的轴承滚珠面型干涉测量方法基于斐索干涉仪,采用特制的标准球面镜作为参考镜,测量精度往往受制于球面镜的加工精度。为了更快速精准地获取轴承滚珠的面型误差,本文基于泰曼-格林干涉光路,开发了一套轴承滚珠面型误差测量系统,以高精度平面镜代替球面镜作为参考镜,避免参考球面镜自身球度误差对测量结果的影响。测量系统通过电荷耦合图像传感器相机(CCD)拍摄五步移相法得到干涉图像,并进行相位提取以得到面型误差。使用最小范数法对五步法相位提取值进行解包裹,采用路径无关算法进行解包裹运算。求解的过程使用预条件共轭梯度法(PCG),将无权重最小二乘法的解包裹结果作为迭代起点,极大地提高了求解速度和稳定性。同时,提出了系统测量过程中离焦倾斜误差处理方法,利用泽尼克多项式进行了波面拟合并进行了相关实验,有效地消除了离焦倾斜误差对系统测量精度的影响。系统对直径D=15 mm的轴承滚珠进行测量,计算得到的波面峰峰值为0.198 9λ,均方根误差为0.024 5λ,与ZYGO干涉仪测量的峰峰值相差0.016λ,均方根误差相差0.004λ。通过多次测量对系统的稳定性进行检验,峰峰值最大偏差为0.013 2λ,均方根误差最大偏差为0.033λ,表明该系统能够有效地对轴承滚珠面型进行检测且测量结果稳定可靠。

1 测量系统光路设计及测量原理

1.1 测距系统光路设计

测量系统原理如图1所示,系统基于泰曼-格林干涉光路,由激光器出射的光束经过空间滤波系统准直扩束后,由分光镜分为两束,一束光经过平面镜反射成为参考光束,另一束光经过透镜、再经滚珠球面反射成为测量光束。两束反射光发生干涉,使用CCD拍摄得到干涉图像。将参考平面镜与压电晶体固定,通过计算机控制压电晶体,获得固定步数的位移,实现移相以获取多幅干涉图像,经图像处理可获得球面面型误差。

图1 测量系统的光路设计

1.2 相移干涉原理

在相移干涉系统测量中,使用压电陶瓷移相系统可实现精确的位移控制,通过压电晶体控制移相步长,移相步长为已知量,干涉光强可以通过CCD得到。当移相次数为5步、步长为σ时,相位φ为

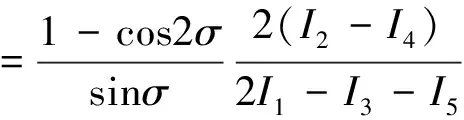
(1)

式中:I1、I2、I3、I4、I5为干涉光强,通过CCD可以测量得到。

当移相步长为π/2时,可得相位

(2)

在测量过程中,理论上五步移相法的I1、I5强度一致,但在实际测量过程中,由于各种误差的影响会出现一定偏差,通过求取平均值,可以减小对测量结果的影响。在一般情况下,移相步数越多,则采样点越多,移相误差越小,实际过程中可根据对噪声的敏感程度选取特定的算法。

相位波面与物体表面高度h变化如下

(3)

2 干涉条纹的相位提取及波面拟合

在CCD获取干涉条纹图像后,对干涉条纹的相位进行提取,包括条纹滤波、包裹相位的提取和相位解包裹。得到解包裹的相位后,需要通过波面拟合消除滚珠定位误差(离焦、倾焦误差),以还原实际的波面,具体流程如图2所示。

图2 干涉图像处理流程

2.1 干涉条纹的滤波及相位解包裹

通过光学干涉方法进行测量时,需要对干涉条纹进行滤波处理来消除环境因素所引入的噪声。本文采用旋转滤波法[8]对干涉条纹进行滤波处理。

图3a为实验测得的原始干涉条纹,图3b为经过旋转滤波后的干涉条纹。从图中可以看出,滤波后干涉条纹比原始条纹更加清晰,在一定程度上消除了图像中存在的噪声点。

(a)原始干涉条纹 (b)滤波后干涉条纹图3 干涉条纹的滤波

根据相移公式可以得到干涉条纹的相位,但是由于被测的面型往往比较复杂,真实相位范围不仅限反正切函数所求得的值,还需要对其进行解包裹[9-11]。

系统采用路径无关算法进行解包裹运算。设原始包裹相位为φi,j,解包裹后相位为φi,j,将解包裹相位数据前后离散偏微分方差的差表示为

(4)

解包裹后相位的偏导数与原始相位偏导数需要趋于一致,因此需要将式(4)取最小值。对式(4)求偏导并令其结果为0,得

(5)

式中

使用预条件共轭梯度法(PCG)进行求解。将无权重最小二乘法的解包裹结果作为迭代起点,采用共轭梯度法进行迭代,如此循环,直至满足收敛条件,结果如图4所示。从中可以看出,相位经过解包裹运算后,由-35 rad扩展到10 rad。

(a)解包裹后相位的二维分布

(b)解包裹后相位的三维分布图4 最小范数法解包裹相位分布图

2.2 波面拟合与离焦倾焦误差的分离

在干涉测量系统中,实际测量过程使用三维调整架对滚珠球心进行微调,难以保证理论上的透镜焦点与球心的精确重合,系统会引入一定的定位误差,包括图5所示的系统离焦和倾焦误差。

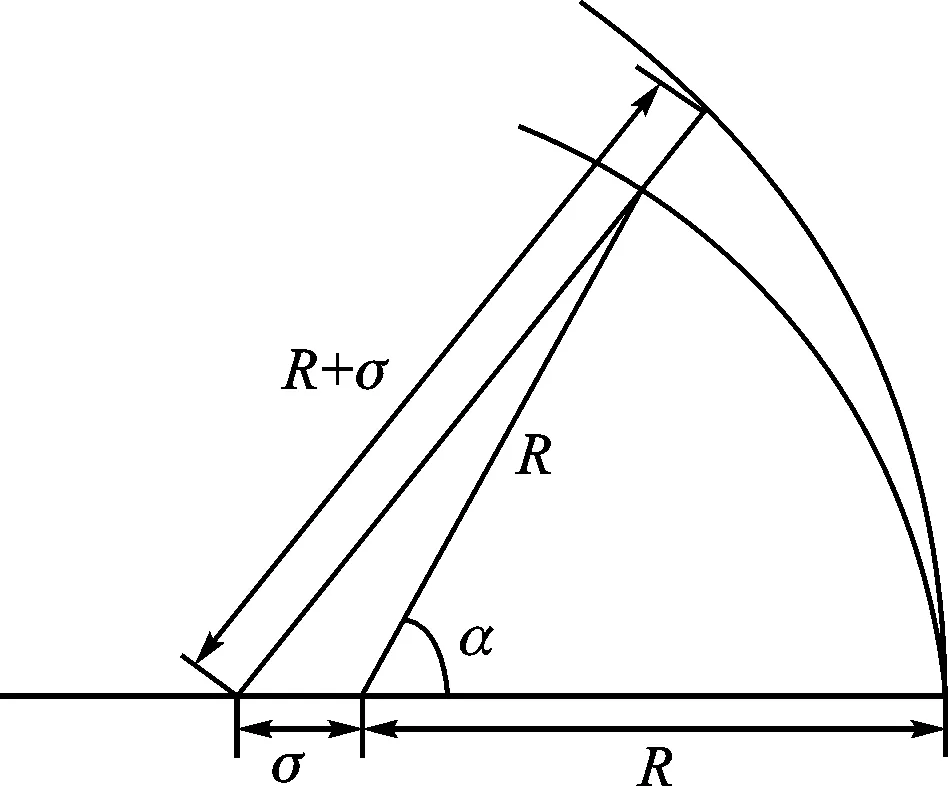
(a)离焦误差

(b)倾焦误差图5 系统离焦、倾焦误差示意图

当系统存在离焦误差时,被测球面沿着光轴移动微小距离σ,R为球面半径,α为孔径角。由几何关系可知,由离焦引入的光程差为

SOPD=2(R+σ)-2(R+σcos(α))=2σ(1-cosα)

(6)

α=arcsin(x2+y2)1/2/R

因(x,y)为球面坐标,当α很小时

cosα=1-sin2α/2

(7)

SOPD=σsin2α=σsin((x2+y2)/R)

(8)

当存在沿x方向的倾斜偏移δx时,由偏移引入的光程差为

SOPD=2xδx/R

(9)

当y方向存在偏移δy时

SOPD=2yδy/R

(10)

光学上的相差和泽尼克多项式相对应,对应关系如表1所示,其中Z1,Z2,Z3,…,Z8表示泽尼克多项式的笛卡尔坐标表示形式。根据式(8)～式(10)可以看出,离焦误差和几何像差的第3项相对应,而沿着x、y方向的倾焦误差分别和像差的第1项和第2项相对应。

波面拟合可以表示为

(11)

式中:w(xk,yk)为拟合得到的数学波面;n=1,2,…,N,N为拟合多项式项数;k=1,2,…,M,M为采样点数。

表1 泽尼克多项式与相差的对应关系

利用泽尼克多项式作为基底函数,线性表示波面[12-13]。已知Tk为实际波面,Zn(xk,yk)为泽尼克多项式,求解系数an的过程即波面拟合。式(11)可以表示为

a1Z1(x,y)+a2Z2(x,y)+…+anZn(x,y)=aTZ

(12)

令qkj=Zj(xk,yk),k=1,2,…,M;j=1,2,…,N,将其代入式(12),得方程组(M>N)

(13)

即

Qa=W

式中:Q=(qk,j)为M×N矩阵;a=(a1,a2,…,aN)T;W=(w1,w2,…,wM)T。式(13)为超定线性方程组,没有一般意义的解,即对任何N维向量,W-Qa≠809。一般选择通过最小二乘法求解,求解步骤如下

(14)

(15)

TkZn(xk,yk)=0

(16)

(17)

Za=c

于是可以得到泽尼克系数方程

(18)

协方差矩阵法避免了复杂的正交过程,通过协方差矩阵的线性变换来求解拟合系数,计算量小,便于编程。协方差矩阵是求解泽尼克系数线性方程的增广矩阵,其表示如下

(19)

通过求解式(19)即可以求得泽尼克多项式系数an。

在拟合过程中,根据具体情况选择泽尼克多项式的项数,一般选择前36项进行拟合。

3 测量系统实验

滚珠面型误差测量系统由干涉光路、压电晶体控制模块、图像采集模块组成。干涉光路是测量系统的核心组件,如图6所示,选取稳频氦氖激光器,其中心波长λ为632.8 nm,输出功率为2 mW,光束直径为1.18 mm。采用Falcon4M30工业黑白相机,4×106像素,2 352×1 728分辨率。

图6 滚珠面型误差测量系统

对直径D=15 mm的轴承滚珠进行测量,清洁表面后将待测滚珠固定,通过采集软件拍摄干涉图像并进行处理。面型检测数据处理过程如下:首先通过五步移相法获取干涉条纹,然后经图像滤波、相位提取、相位解包裹、泽尼克拟合,最后剔除离焦项和倾焦项,即可得到波面并求得面型误差。

利用36项泽尼克多项式对实际解包裹后的相位进行拟合,结果如图7所示。

泽尼克多项式拟合所得数字波面与解包裹后相位波面变化趋势相同。泽尼克多项式拟合波面为数字波面,其表面平滑,而解包裹后相位携带波面误差,表面变化存在许多噪声点。通过协方差矩阵法对泽尼克系数进行求解,拟合系数前3项分别为a1=-4.647 1,a2=8.793 6,a3=-17.536 7。

剔除倾焦、离焦项后的波面可以表示为

(20)

(a)解包裹后的相位波面

(b)泽尼克多项式拟合波面

(c)消除离焦、倾焦误差后的波面

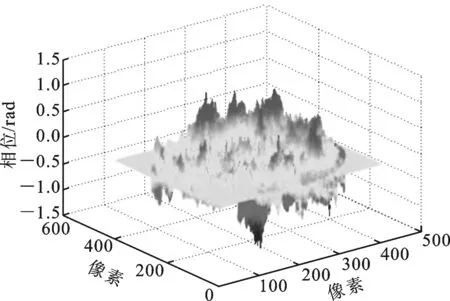
(d)消除离焦、倾焦误差后的波面三维图图7 解包裹相位波面拟合结果

消除离焦、倾焦误差后波面如图7c所示,波面最大值为1,最小值为-1.5。可以看出,原始相位中存在一定的离焦、倾焦误差被剔除,相位波面总体趋于平面波面。利用泽尼克多项式拟合可以达到理想的效果,能消除系统中存在的离焦、倾焦误差。通过相关公式可以获得滚珠表面面型误差信息,得到误差图像。

光学元件的表面面型常用的评价指标是波峰波谷之间的距离DPV与均方根误差δRMS,计算方法为

DPV=ωmax-ωmin

(21)

(22)

通过得到的数据与相关公式,计算得到滚珠的测量结果DPV=0.198 9λ,δRMS=0.024 5λ。利用ZYGO VeriFireRMXPZ干涉仪进行测量结果评估,系统得到的结果与ZYGO干涉仪测量结果DPV值相差0.016λ,δRMS相差0.004λ,具体数据见表2。

表2 直径D=15 mm的轴承滚珠测量结果

ZYGO干涉仪的测量精度小于λ/100(DPV),在进行球面测量时,系统精度主要受限于测量标准参考球面镜精度λ/20(DPV)。通过实验结果可以看出,系统测量结果与ZYGO干涉仪测量结果相差0.001 6λ,在误差范围内测量结果可靠。此外,系统所测结果(DPV,δRMS)均大于ZYGO干涉仪测量结果,这是实际测量系统的移相误差和CCD的非线性误差等因素导致的系统误差,因此通过减小系统的移相误差和CCD非线性误差等可以进一步提高系统测量精度。

测量系统所得的是部分球面面型误差,通过多次测量可以获得整个球面面型误差值。DPV和δRMS反映的是面型误差的平均水平,因此测量系统可以准确地评价球面面型精度。

为了检测系统的重复精度即测量的稳定性,另取一直径D=15 mm的轴承滚珠进行了多次测量,9次测量值如表3所示。

表3 系统稳定性测试

对轴承滚珠9次测量的平均值DPV=0.266 9λ,δRMS=0.045 6λ,DPV值最大偏差为0.013 2λ,δRMS最大偏差为0.033λ,说明系统具有较高的测量重复精度。测量的随机误差与设备和环境的稳定性有关,在实际测量时可多次测量求平均值来减小随机误差对测量结果的影响。

4 结 论

本文设计了一种基于泰曼-格林干涉光路的轴承滚珠面型误差测量系统,以平面参考镜代替球面参考镜,以减小球面镜自身球度误差对测量结果的影响。系统通过五步移相法得到干涉图像,使用最小范数法对五步法相位提取值进行解包裹,并采用路径无关算法进行解包裹运算。对于系统测量过程中产生的离焦、倾焦误差,采用泽尼克多项式波面拟合的方法以剔除误差项,并利用协方差矩阵法进行拟合系数的求解,保障了测量结果的可靠性。本文还进行了直径D=15 mm的滚珠测量实验并与ZYGO干涉仪的测量结果比较,波峰波谷值DPV相差0.016λ,均方根误差δRMS相差0.004λ。此外,对系统的稳定性进行了测试,结果表明,本文方法可以有效实现滚珠的面型测量且结果可靠。本文所研究的泰林-格曼型轴承滚珠面型激光干涉测量系统主要用于小批量高精度要求的滚珠测量及其他圆度测量,对于大批量精密滚珠轴承的测量,还需进一步研究,以提高其适用性。

[1] LIPA J A, SIAADLL G J. High precision measurement of gyro rotor sphericity [J]. Precision Engineering, 1980, 2(3): 123-128.

[2] 邓忠文, 刘志刚, 陶龙, 等. 新型可调谐外腔半导体激光器光频扫描干涉测距方法 [J]. 西安交通大学学报, 2013, 47(5): 104-109 DENG Zhongwen, LIU Zhigang, TAO Long, et al. Novel frequency scanned interferometry absolute distance measurement by tunable external-cavity diode laser [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 104-109.

[3] 彭建华, 沈亦兵, 汪凯巍, 等. 球面绝对检测方法的误差影响分析及实验研究 [J]. 红外与激光工程, 2012, 41(5): 1345-1350. PENG Jianhua, SHEN Yibing, WANG Kaiwei, et al. Error impact analysis and experimental research for

absolute testing of spherical surfaces [J]. Infrared and Laser Engineering, 2012, 41(5): 1345-1350.

[4] 王道档, 杨甬英, 陈晓钰, 等. 高精度球面检测中调整误差的精确校正 [J]. 纳米技术与精密工程, 2013, 11(1): 20-26. WANG Daodang, YANG Yongying, CHEN Xiaoyu, et al. Accurate calibration of misalignment in high-precision spherical surface testing [J]. Nanotechnology and Precision Engineering, 2013, 11(1): 20-26.

[5] MANTRAVADI M V, MALACARA D. Newton, Fizeau, and Haidinger interferometers [M]. Hoboken, USA: John Wiley & Sons Inc., 2006: 1-45.

[6] KIMBROUGH B, MEDOWER B, MILLERD J. Dynamic Fizeau interferometers [C]∥ Fringe 2009. Berlin, Germany: Springer, 2009: 1-10.

[7] XU Jiancheng, SUN Lili, LI Yanli, et al. Principal component analysis of multiple-beam Fizeau interferograms with random phase shifts [J]. Optics Express, 2011, 19(15): 14464-14472.

[8] 徐建程, 许乔, 柴立群, 等. 基于旋转滤波法的干涉条纹预处理技术 [J]. 强激光与离子束, 2006, 18(1): 69-72. XU Jiancheng, XU Qiao, CHAI Liqun, et al. A new fringe-pattern preprocess method based on median spin filtering [J]. High Power Laser & Particle Beams, 2006, 18(1): 69-72.

[9] GODLSTEIN R M, ZEBKER H A, WERNER C L. Satellite radar interferometry: two-dimensional phase unwrapping [J]. Radio Science, 1988, 23(4): 713-720.

[10]FLYNN T J. Two-dimensional phase unwrapping with minimum weighted discontinuity [J]. Journal of the Optical Society of America: A, 1997, 14(10): 2692-2701.

[11]GHIGLIA D C, PRITT M D. Two-dimensional phase unwrapping theory algorithms and software [M]. New York, USA: John Wiley & Sons Inc., 1998.

[12]WANG J Y, SILVA D E. Wave-front interpretation with Zernike polynomials [J]. Applied Optics, 1980, 19(9): 1510-1518.

[13]单宝忠, 王淑岩, 牛憨笨, 等. Zernike多项式拟合方法及应用 [J]. 光学精密工程, 2002, 10(3): 318-321. SHAN Baozhong, WANG Shuyan, NIU Hanben, et al. Zernike polynomial fitting method and its application [J]. Optics & Precision Engineering, 2002, 10(3): 318-323.

(编辑 杜秀杰)

Surface Error Measurement System for Bearing Ball with Laser Interferometry

HAO Weina,LING Fengchao,LIU Zhigang,HONG Jun,ZHU Yongsheng

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

To avoid the influence from sphericity error of spherical mirror on the results in bearing ball measurement with laser interferometry, a Tyman-Green interference method by a plane reference mirror instead of a spherical mirror for the spherical surface error measurement of bearings ball is proposed and a prototype interferometer is developed. Following phase shifting interferometry principle, the interferometer system controls piezoelectric ceramic transducer phase shifter to move the plane reference mirror to obtain more interference images. The images are captured by charge-coupled device camera and then the spherical surface error is evaluated by phase unwrapping. Zernike polynomials fitting is chosen to eliminate the alignment errors from out-off-focus. Experiments verify its effectiveness and robustness, and the root mean square difference of results between surface error measurement system and ZYGO interferometer system is 0.004λwhile the difference of peak-to-peak value is 0.001 6λbetween the two systems. The method can be expected to apply to the other fields of roundness measurement.

phase-shift interferometry; bearing ball; wavefront fitting; alignment error

2015-12-03。 作者简介:郝维娜(1989—),女,博士生;刘志刚(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51375376)。

时间:2016-03-15

10.7652/xjtuxb201606013

TH741

A

0253-987X(2016)06-0083-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160315.1631.002.html