车辆多目标自适应巡航控制算法
2016-12-23张亮修吴光强郭晓晓
张亮修,吴光强,2,郭晓晓
(1.同济大学汽车学院,201804,上海;2.东京大学生产技术研究所,153-8505,东京)
车辆多目标自适应巡航控制算法
张亮修1,吴光强1,2,郭晓晓1
(1.同济大学汽车学院,201804,上海;2.东京大学生产技术研究所,153-8505,东京)
为了综合协调车辆跟车时的追踪性能、燃油经济性能、驾乘人员舒适性能和跟车安全性能,研究了多目标自适应巡航控制(ACC)算法,建立了包含车辆模型和车间关系的ACC系统集成式纵向运动学模型,设计了描述追踪误差、燃油消耗量和驾驶员跟车行为误差的目标函数,以及保证动态跟车、期望驾乘感受和跟车安全的约束条件,基于模型预测控制理论将多目标ACC系统控制算法转化为带有多个约束的在线二次规划问题。采用反馈校正机制改善了算法设计时存在的建模失配和外部干扰等低鲁棒性问题,引入向量松弛因子解决了优化求解过程中硬约束导致的控制算法非可行解问题。仿真结果表明,相比线性二次型调节器的ACC算法,所提控制算法在前车循环工况中100 km油耗降低9.3%,追踪误差指标降低21.7%,从而实现了良好的车辆追踪,同时满足驾驶员期望的跟车特性要求。
自适应巡航控制;多目标;模型预测控制;反馈校正;向量松弛因子
作为传统巡航系统的增强升级技术,自适应巡航控制(ACC)系统可以提高驾驶舒适性,降低疲劳强度,改善驾驶安全性。过去很长一段时间,对ACC的研究主要集中在追踪期望间距或者期望速度方面。近年来,ACC的研究呈现多元化,如适用于城市工况的启-停ACC[1]、混合动力汽车加装ACC[2]、将ACC与车道保持系统相结合[3]、弯道行驶ACC[4]、考虑燃油经济性的ACC[5]等。研究表明,ACC的使用可以减少燃油消耗,而考虑驾驶员期望感受的ACC会大大提高驾乘舒适性[6]。
跟车时车辆的追踪性能、燃油经济性能与驾驶员期望感受及行车安全性之间存在着一定冲突[7-8],改善燃油经济性往往意味着降低加速性能、弱化追踪能力,而过于关注追踪性能的ACC系统往往会导致车辆频繁加、减速,从而恶化车辆燃油经济性,引起驾驶员不适,并给行车安全带来隐患。
本文基于模型预测控制理论,发展了一种综合考虑车辆追踪性能、燃油经济性能、驾乘人员舒适性能并保证跟车安全的车辆多目标ACC算法,采用反馈校正机制和向量松弛因子分别解决了控制算法低鲁棒性和非可行解的问题。
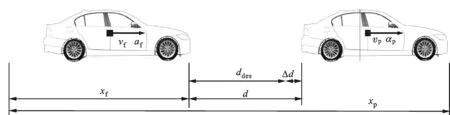
图1 ACC纵向运动学示意图
1 ACC集成式纵向运动学建模
图1给出了ACC自车与前车之间的纵向运动学关系,并定义
(1)
式中:Δd为车间距误差;Δv为前车和自车相对速度;d、ddes分别为实际车间距和期望车间距;vp、vf分别为前车和自车速度。
本文中,期望车间距采用固定车间时距[9],即
ddes=τhvf+d0
(2)
式中:τh为车间时距;d0为自车停止后与前车最小安全车距。
自车实际加速度af和期望加速度af,des的关系用一阶惯性环节表示[10],即
(3)
式中:KL为系统增益;TL为时间常数。
以Δd、Δv、af为状态变量,以af,des为控制输入,把ap看作系统扰动,得到如下状态方程
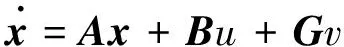
y=Cx
(4)
式中
式(4)可控阵为
当其秩数为3时,系统状态完全可控。因式(4)输出状态系数矩阵C为单位阵,所以输出也完全可控。对式(4)进行离散,得到线性离散状态空间方程
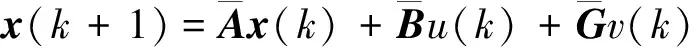
(5)
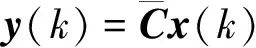
(6)
Ts为采样周期时,其他系数矩阵分别为
2 车辆多目标ACC性能指标
采用二次型性能指标和线性不等式约束形式分别设计了ACC纵向跟车时的追踪性能、燃油经济性能、驾乘人员舒适性能等指标,以及安全跟车条件和其他有关约束[7]。
2.1 追踪性能指标
ACC纵向跟车时的追踪性能主要通过车间距误差和相对车速来评价,需满足2个子目标:①当前车稳态行车时,车间距误差和相对车速均要收敛为0;②前车动态行车时,车间距误差和相对车速均处于自车驾驶员期望追踪误差的范围之内。
第1个追踪子目标用相对车速和车距误差的二次型表示[11],即
JT=wΔvΔv2+wΔdΔd2
(7)
式中:JT为追踪性能指标;wΔv、wΔd分别为相对车速和车距误差的权系数。
当前车突然加、减速时,为防止自车加速和制动能力不足,对车间距误差及相对车速进行约束,以保证第2个追踪子目标,即
Δdmin≤Δd≤Δdmax
Δvmin≤Δv≤Δvmax
(8)
式中:Δdmax和Δdmin分别为车间距误差的上、下界;Δvmin和Δvmax分别为相对车速的上、下界。
2.2 燃油经济性能指标
燃油经济性目标是使得自车跟车过程中的油耗最低,燃油消耗与纵向加速度密切相关,降低自车加速度可有效提高车辆的燃油经济性。利用期望加速度和期望加速度导数的二次型来间接表示燃油经济性指标,即
(9)
式中:JE为燃油经济性指标;wEa、wEda分别为期望加速度和期望加速度导数对应的权系数。
最小化JE可降低车辆的加速度和加速度变化率,限制发动机转速频繁变化,有助于提高燃油经济性,同时较低的纵向加速度变化率可减小纵向冲击,提高成员的纵向乘坐舒适性。
2.3 驾乘人员舒适性能指标
良好的驾乘人员舒适性能需符合3个子目标:①实际车距与期望车距保持相等;②车辆纵向加速度和纵向加速度导数均保持在驾驶员容许的范围[12];③符合驾驶员动态跟车特性。
第1个舒适性能子目标已经在ACC集成式运动学模型中体现。第2个舒适性能子目标利用约束期望加速度和实际加速度的措施来反映,即
(10)

第3个舒适性能子目标针对跟车过程,虽然最终目标是使Δv和Δd收敛至0,但前车在切入/切出或者加、减速工况中追踪误差并不为0,这时驾驶员往往会按照自己期望的加速度来操纵加速踏板和制动踏板,使追踪误差收敛。因此,利用驾驶员参考加速度模型与跟车系统实际输出之差的二次型表示驾乘人员舒适性能的第3个子目标,即
JC=wCa(af,ref-af)2
(11)
式中:JC为驾乘人员舒适性能指标;af,ref=kvΔv+kdΔd为自车驾驶员参考加速度[13];wCa为对应权系数。
2.4 安全跟车条件
为保证行车安全,动态跟车过程中的车间距必须大于0,以避免追尾碰撞事故发生。动态跟车过程中的安全车间距与车速相关,为非固定值。碰撞时间(time-to-collision,TTC)可描述制动过程的跟车安全性,但TTC并不适用于稳态跟车过程[14]。综合TTC和固定安全车距设计的安全跟车条件为
d≥ds
ds=max{tTTCΔv,ds0}
(12)
式中:tTTC为碰撞时间;ds为跟车安全车距;ds0为跟车最小安全距离。
2.5 多目标ACC目标函数和约束条件
多目标ACC中,JT、JE和JC是相互影响、相互关联的,利用加权将三者整合为统一目标函数,则有
J=JT+JE+JC=(wΔvΔv2+wΔdΔd2)+
(13)
[4]将式(13)转化为预测型目标函数,假定当前时刻为k,在预测时域i∈[k:k+p-1]和控制时域i∈[k:k+c-1]内,保持目标函数的函数类型和权系数不变,并以第i点的预测输入和预测输出为自变量,建立第i点的离散目标函数,再将各点的目标函数线性加权,得到目标函数
(14)
式中:Δu(k+i|k)=u(k+i|k)-u(k+i-1|k)为控制量增量;my为输出转换矩阵,wy、wEa、ΔwEa分别为系统输出权系数、控制量权系数、控制量增量权系数,相应表达式为
由式(8)、式(10)建立的多目标ACC的输入、输出约束条件为
(15)

由式(12)建立的安全跟车约束为
asy(k+i+1|k)≥ds(k)-ddes(k)
(16)

3 模型预测多目标ACC控制算法
3.1 反馈校正跟车预测模型
受车辆参数不完全确定和外部干扰的影响,跟车预测模型与其实际状态之间不可避免地存在着一定偏差,采用反馈校正机制可提高跟车预测模型的鲁棒性[15]。
定义k时刻跟车系统实际状态与跟车预测状态之间的误差
e(k)=x(k)-x(k|k-1)
(17)
式中:x(k)为k时刻的跟车系统实际状态;x(k|k-1)为k-1时刻对k时刻状态的预测。借助式(5)可以得到

(18)
式中:x(k-1)、u(k-1)和v(k-1)分别为k-1时刻的状态量、控制输入和外部干扰。
在k时刻,为提高离散跟车模型的预测精度,利用误差e(k)校正状态预测量x(k+1|k),则有
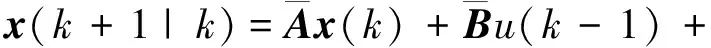

(19)
式中:Δu(k+0|k)为(k+0|k)时刻的控制增量;H为校正矩阵
H=diag(h1,h2,h3)
(20)
借助式(6),可由式(19)推导出以p为预测时域、以c为控制时域的跟车预测模型的矩阵形式
Y=[Mx+MeH]x(k)+Muu(k-1)+
MΔuΔU-MeHx(k|k-1)+MvV
(21)
式中
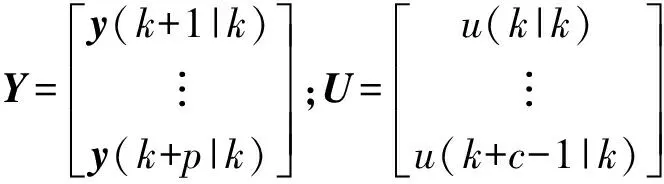
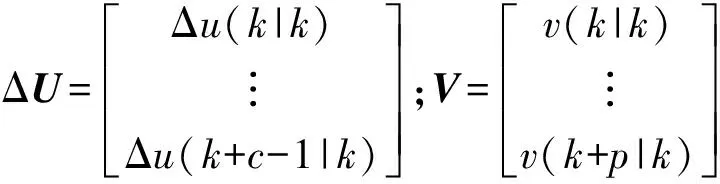
其中:Y为预测时域的系统输出;U为预测控制输入;ΔU为预测控制增量;V为预测外部干扰。其他各个预测矩阵表达式分别为
式(21)表示预测时域内系统预测输出Y与预测控制增量ΔU的关系,而预测控制输入U和预测控制增量ΔU并不相互独立,它们之间服从以下关系
u(k+i|k)=u(k+i-1|k)+Δu(k+i|k)
i=0,…,c-1
(22)
将式(22)代入预测控制输入U的定义式,整理后有
U=Tuu(k-1)+TΔuΔU
(23)
式中
3.2 向量松弛因子软化硬约束
通常,模型预测优化采用硬约束会出现无可行解的问题[16]。文献[7,15]采用标量松弛因子对硬约束进行整体软化,但对于不同的约束无法区别对待,故本文采用向量松弛因子对硬约束进行软化来扩展解的可行域,利用软约束的可调整性放松系统输入或输出的上、下边界,使预测优化问题有可行解。
在多目标ACC约束条件中,式(15)主要反映驾乘人员对舒适性能和追踪误差的可接受程度,放松该约束边界会导致舒适性能和追踪性能弱化,但不影响ACC正常工作。式(16)为安全跟车条件约束,放松该约束边界可能导致自车与前车追尾。为此,只对式(15)进行约束软化,即
(24)
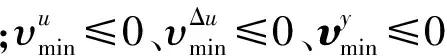
被软化的约束边界不能被无限放松,在目标函数中需要对松弛因子进行限制,即
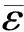
(25)

3.3 多目标ACC控制算法转化
联合式(14)、式(25),推导出矩阵型目标函数
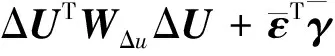
(26)
式中
My=diag(my,my,…,my)
Wy=diag(wy,wy,…,wy)
Wu=diag(wEda,wEda,…,wEda)
WΔu=diag(ΔwEda,ΔwEda,…,ΔwEda)
将式(21)代入式(26),多目标ACC控制算法(简称ACC算法)的设计最终转化为带有约束的在线二次规划问题,即
(27)
式中
其中
MeHx(k|k-1)-MvV
MeHx(k|k-1)+MvV
Muu(k-1)-MeHx(k|k-1)+MvV]
在滚动优化求解过程中,当输入或输出值超出硬约束边界时,向量松弛因子会自动调节,放松输入或输出约束的上、下边界,保证Δu(k+i|k)有最优解。在每一个采样周期,多目标ACC系统根据当前状态对未来状态进行预测,并进行反馈校正,然后利用式(27)完成最优求解后得到控制时域内的一系列控制输入增量和松弛因子,即
(28)

u*(k)=Δu*(k)+u(k-1)
(29)
进入下一个采样时刻后,重复上述过程,通过在线滚动优化将实现多目标ACC控制。
4 仿真验证
本文在MatlabSimulink环境下仿真验证了多目标ACC算法,仿真参数见表1。

表1 多目标ACC仿真参数
为验证本文多目标ACC算法性能进行了仿真,并与文献[17]采用的LQR控制算法(简称LQR算法)进行了对比。仿真工况如下:①前车急加速工况;②前车急减速工况;③前车循环工况。考虑到舒适性要求,在LQR算法中对加速度进行限制,相应参数选取与本文多目标ACC算法相同,其控制规律为
(30)
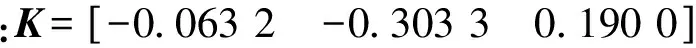
4.1 前车急加速工况
前车急加速工况中,前车和自车初始速度相同,5 s时前车以1 m/s2加速度加速到22 m/s,仿真结果如图2~图5所示。为便于仿真对比,LQR算法控制结果用LQR-ACC表示,本文多目标ACC算法控制结果用MPC-ACC表示。

图2 前车急加速工况车辆速度曲线

图3 前车急加速工况车辆加速度曲线
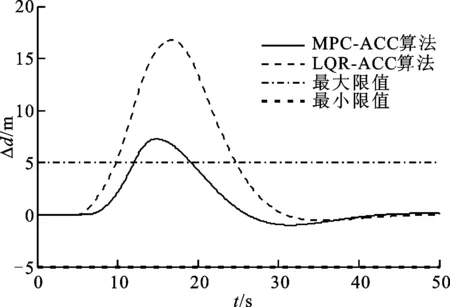
图4 前车急加速工况车间距误差曲线
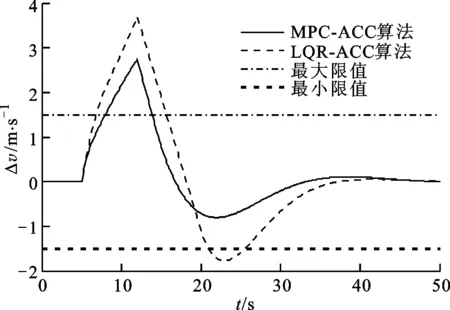
图5 前车急加速工况相对速度曲线
由图2可知,MPC-ACC算法和LQR-ACC算法都可以实现跟车功能,前车加速时,自车相应加速,前车稳态行驶时,自车与前车相对速度最终均收敛于0,但相对于LQR-ACC算法,MPC-ACC算法对应的车速峰值较小,收敛速度较快。由图5中前车和自车的相对速度来看,LQR-ACC算法的相对速度要大于MPC-ACC算法。由图4可知,LQR-ACC算法的车间距误差峰值近乎是MPC-ACC算法的3倍。可见,本文MPC-ACC算法能更有效地追踪期望车间距,实现驾驶员期望反应。从图3可以看出,MPC-ACC算法加速度基本保持在限值之内,但在前车急加速段,由于车间距误差、相对速度约束和松弛因子的作用,即自车为满足追踪性,使得其加速度略微超出限值,但仍在驾驶员舒适性可接受的范围之内。
4.2 前车急减速工况
前车急减速工况中,前车和自车初始速度相同,5 s时前车以-2 m/s2减速度减速到10 m/s。LQR-ACC算法和MPC-ACC算法的仿真结果如图6、图7所示。
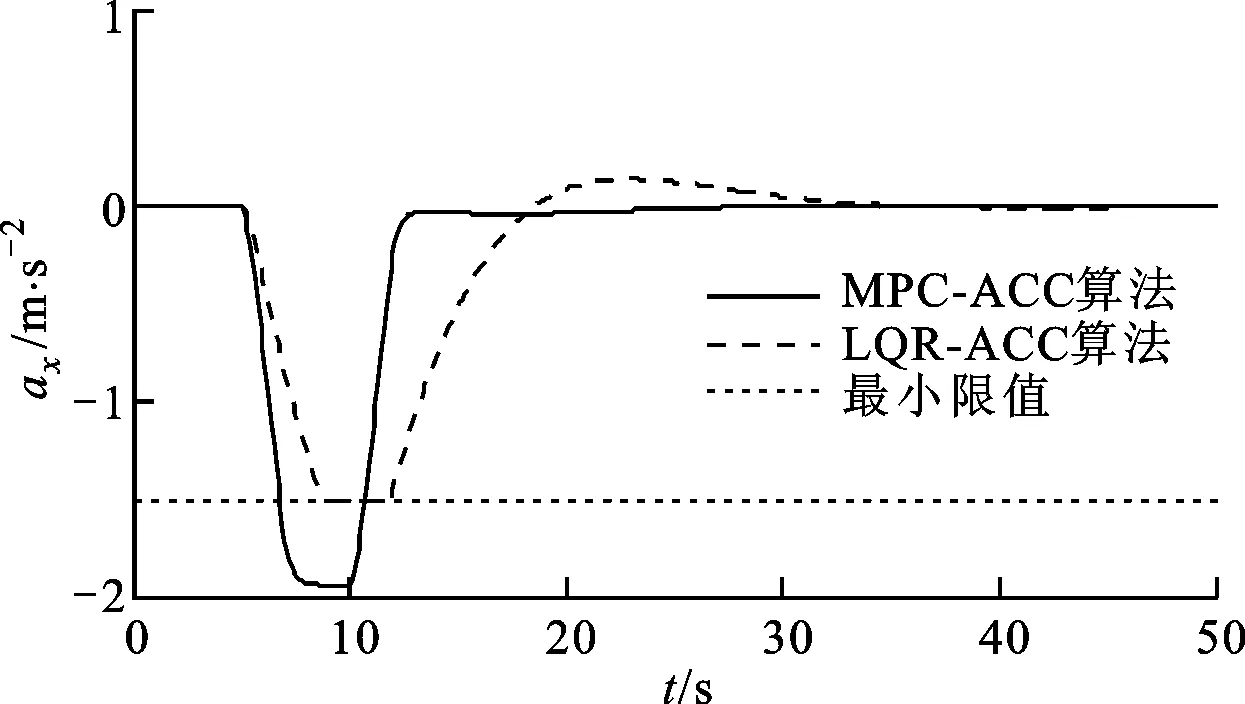
图6 前车急减速工况加速度曲线

图7 前车急减速工况车间距曲线
在前车急减速工况下安全性是第一位的,即自车与前车的车间距应远大于安全距离。由图7可知,在此工况下MPC-ACC算法车间距远大于安全距离,满足安全性要求,而LQR-ACC算法车间距虽然也大于安全距离,但安全性远不如MPC-ACC算法,当前车以更大减速度减速时,很可能出现由于减速能力不足使得车间距小于安全距离,甚至出现撞车的情况。由图6可知,MPC-ACC算法可以自动调整车辆加速度,实现车辆较大减速能力,可以超出约束要求而保证行车安全性。由图7还可知,MPC-ACC算法加速度虽超出限值,但仍在驾乘人员舒适性可接受的范围之内。
4.3 前车循环工况
前车循环工况模拟高速公路行车时,前车用小加速度、大车速变化行驶的舒缓交通流。图8为前车循环工况下前车速度变化。在此工况下,用追踪误差指数eTEI来表征车辆追踪性能。

图8 前车循环工况下前车速度变化
追踪误差指数定义如下[7]
(31)
式中:ξDV为权系数,用于反映对Δd(k)、Δv(k)重视程度,取0.1。追踪误差指数越小,车辆追踪性能越好。
车辆燃油经济性按照文献[18]半经验油耗模型计算,以100 km油耗作为燃油经济性的评价指标,则有
(32)
式中:Qs为车辆瞬时油耗;ρg=0.725 g/mL为汽油密度。
由式(31)计算可得MPC-ACC算法下eTEI为0.4296,LQR-ACC算法下eTEI为0.548 5;由式(32)计算可得MPC-ACC算法下100 km油耗为7.5 L,LQR-ACC算法下100 km油耗为8.2 L。因此,前车循环工况下,MPC-ACC与LQR-ACC相比,100 km油耗降低了9.3%,追踪误差指标降低了21.7%,这说明本文多目标ACC系统可同时提高车辆的追踪性能和燃油经济性能。
5 结 论
(1)将前车加速度看作系统扰动,建立了包含车辆模型和车间关系的ACC系统集成式纵向运动学模型。
(2)设计描述追踪误差、燃油消耗量和驾驶员跟车行为误差的目标函数,以及保证动态跟车、期望驾乘感受和跟车安全的约束条件,基于模型预测控制理论,将多目标ACC算法转化为带约束的二次规划问题。
(3)采用反馈校正机制改善算法设计时存在的建模失配和外部干扰等低鲁棒性问题,引入向量松弛因子解决优化求解过程中硬约束导致的控制算法非可行解问题。
(4)基于Matlab/Simulink验证了多目标ACC算法,仿真表明,本文算法能实现良好的车辆追踪的同时,还能满足驾驶员期望跟车特性的要求。
参考文献:
[1] SHAKOURI P, ORDYS A, ASKARI M R. Adaptive cruise control with stop & go function using the state-dependent nonlinear model predictive control approach [J]. ISA Transactions, 2012, 51(5): 622-631.
[2] GANJI B, KOUZANI A Z, KHOO S Y, et al. Adaptive cruise control of a HEV using sliding mode control [J]. Expert Systems with Applications, 2014, 41(2): 607-615.
[3] DANG R, WANG J, LI S E, et al. Coordinated adaptive cruise control system with lane-change assistance [J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 1-11.
[4] 张德兆. 基于弯道行驶的车辆自适应巡航控制 [D]. 北京: 清华大学, 2011: 73-74.
[5] LI S E. Economy-oriented vehicle adaptive cruise control with coordinating multiple objectives function [J]. Vehicle System Dynamics, 2012, 51(1): 1-17.
[6] 罗莉华. 汽车自适应巡航控制及相应宏观交通流模型研究 [D]. 杭州: 浙江大学, 2011: 55-66.
[7] LI S, LI K, RAJAMANI R, et al. Model predictive multi-objective vehicular adaptive cruise control [J]. IEEE Transactions on Control Systems Technology, 2011, 19(3): 556-566.
[8] 吴光强, 郭晓晓, 张亮修. 汽车自适应巡航跟车多目标鲁棒控制算法设计 [J]. 哈尔滨工业大学学报, 2016, 48(1): 80-86. WU Guangiqang, GUO Xiaoxiao, ZHANG Liangxiu. Multi-objective robust adaptive cruise control algorithm design of car following model [J]. Journal of Harbin Institute of Technology, 2016, 48(1): 80-86.
[9] YI K, KWON Y D. Vehicle-to-vehicle distance and speed control using an electronic-vacuum booster [J]. JSAE Review, 2001, 22(4): 403-412.
[10]MARTINEZ J J, CANUDAS-DE-WIT C. A safe longitudinal control for adaptive cruise control and stop-and-go scenarios [J]. IEEE Transactions on Control Systems Technology, 2007, 15(2): 246-258.
[11]BAGESHWAR V L, GARRARD W L, RAJAMANI R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles [J]. IEEE Transactions on Vehicular Technology, 2004, 53(5): 1573-1585.
[12]FERRARA A, PISU P. Minimum sensor second-order sliding mode longitudinal control of passenger vehicles [J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(1): 20-32.
[13]BOER E, NICHOLAS W, MICHAEL M, et al. Driver-model based assessment of behavioral adaptation [J]. Transactions of the Society of Automotive Engineers of Japan, 2006, 37(4): 21-26.
[14]张磊. 基于驾驶员特性自学习方法的车辆纵向驾驶辅助系统 [D]. 北京: 清华大学, 2009: 24-25.
[15]李升波, 王建强, 李克强, 等. MPC实用化问题处理及在车辆ACC中的应用 [J]. 清华大学学报(自然科学版), 2010, 50(5): 645-648. LI Shengbo, WANG Jianqiang, LI Keqiang, et al. Processing of MPC practical problems and its application to vehicular adaptive cruise control systems [J]. Journal of Tsinghua University (Sci & Tech), 2010, 50(5): 645-648.
[16]GARCIA C E, PRETT D M, MORARI M, et al. Model predictive control: theory and practice: a survey [J]. Automatica, 1989, 25(3): 335-348.
[17]李朋, 魏民祥, 侯晓利. 自适应巡航控制系统的建模与联合仿真 [J]. 汽车工程, 2012, 34(7): 622-626. LI Peng, WEI Minxiang, HOU Xiaoli. Modeling and co-simulation of adaptive cruise control system [J]. Automotice Engineering, 2012, 34(7): 622-626.
[18]CAPPIELLO A, CHABINI I. A statistical model of vehicle emissions and fuel consumption [C]∥Proceedings of IEEE 5th International Conference on ITS. Piscataway, NJ, USA: IEEE, 2002: 801-809.
(编辑 苗凌)
Vehicular Multi-Objective Adaptive Cruise Control Algorithm
ZHANG Liangxiu1,WU Guangqiang1,2,Guo Xiaoxiao1
(1. School of Automotive Studies, Tongji University, Shanghai 201804, China; 2. Institute of Industrial Science, The University of Tokyo, Tokyo 153-8505, Japan)
To comprehensively coordinate tracking capability, fuel economy, driver comfortable response and car-following safety, a vehicular multi-objective adaptive cruise control (ACC) algorithm is designed, and an integrated longitudinal kinematic model of ACC system including vehicle model and its relationship with preceding vehicle is established. The quadratic objective functions that consider the contradictions between minimal tracking error, low fuel consumption and driver dynamic car-following behavior are developed, and the linear constraints that ensure dynamic car-following, desired comfortable response and driving safety are designed. Following model predictive control theory, the design of multi-objective ACC algorithm can be transformed into an online quadratic programming problem with multi-constraints. Adopting feedback correction mechanism, the modeling mismatch and external disturbances are greatly weakened to improve the control system robustness. Vector relaxation factors are introduced to deal with the non-feasible solution from hard constraints in the optimization process. The simulations show that the proposed algorithm can reduce fuel consumption by 9.3% and decrease tracking error index by 21.7% compared with LQR case in preceding vehicle cycle scenario, thus a good vehicle tracking is realized and the driver desired car following characteristics are satisfied.
adaptive cruise control; multi-objective; model predictive control; feedback correction; vector relaxation factors
2016-04-09。 作者简介:张亮修(1982—),男,博士生;吴光强(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51575393);上海汽车工业科技发展基金会资助项目(1526)。
10.7652/xjtuxb201611021
TU273
A
0253-987X(2016)11-0136-08
