机床滚转角高精度测量中的频偏现象研究

余宝,王昭,黄军辉,齐静雅,李朝晖,郭俊杰

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械系统工程国家重点实验室,710049,西安;3.陕西恒通智能机械有限公司,710049,西安)



机床滚转角高精度测量中的频偏现象研究

余宝1,王昭1,黄军辉1,齐静雅2,李朝晖2,郭俊杰3

(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械系统工程国家重点实验室,710049,西安;3.陕西恒通智能机械有限公司,710049,西安)

为降低正交偏振光外差干涉相位法中相位差的波动幅度,提高滚转角的测量精度,利用琼斯矩阵法,建立了测量光路和参考光路数学模型。新模型在原有模型的基础上考虑了双频激光器频差的不稳定性和光电探测器响应时间的差异性的影响,推导出测量信号和参考信号之间的频率偏差(简称频偏)会对相位差波动产生较大的影响。在此基础上,给出频偏是由双频激光器频差的不稳定性和光电探测器响应时间的差异性综合作用产生的,并且量化了频偏对于滚转角测量精度的影响。根据该模型,提出通过提高双频激光器的稳频精度和降低光电探测器的响应时间的差异性的方法来降低频偏,进而降低相位差波动。实验结果表明:在降低光电探测器响应时间的差异性后,相位差实际波动幅度由0.7°下降到0.1°左右,测量误差降低了85.7%,证明了分析模型有效可行。

相位差;滚转角;频偏;精度

基于直角坐标系统的机床或测量机共有21项结构误差,其中滚转角误差参数测量较困难。目前,国内外针对滚转角的测量做了大量的研究,其中基于拍频信号相位检测的外差干涉法以其非接触、高灵敏度、光路简单等优点有着良好的应用前景。前苏联Coronkevich等最先提出利用纵向塞曼激光器实现滚转角的测量[1]。清华大学蒋弘等提出基于横向塞曼激光器的非线性滚转角测量方法,使用1/4波片将正交的线偏振光椭偏化,极大地增加了滚转角测量的灵敏度[2]。在此基础上,柳忠尧等提出改进方案,用1/2波片替代偏振片作为敏感元件,并通过角锥棱镜折返两次通过1/2波片,灵敏度是改进前的4倍[3]。这类方案都是通过检测拍频的相位差,进而推算出滚转角的大小,因此相位差值的准确及稳定与否将直接决定滚转角的测量精度和不确定度。

本文基于文献[3-4]的方案,论述了测量基本原理,并建立了频偏产生的数学模型,仿真和实验分析了频偏对于相位波动的影响,最后给出了减小和消除频偏的方法。

1 滚转角测量

1.1 测量原理

基于相位的激光外差滚转角测量系统如图1所示。塞曼双频激光器发出正交线偏振光,经分光棱镜,其中反射光经过检偏器被光电探测器接收作为参考信号;透射光分别经过1/4波片、1/2波片,经过直角棱镜反射后,再次经过1/2波片,最后经过检偏器被光电探测器接收作为测量信号。1/2波片作为角测量传感器随被测物体运动,当存在滚转误差时,1/2波片随之转动,进而引起测量信号和参考信号之间的相位差发生变化,因此可以根据相位差变化量进而求出滚转误差的大小。本研究使用成都工具研究所研制的MJS5200型He-Ne纵向塞曼激光器,通过在内部安装1/4波片,从而使其出射正交线偏振光。

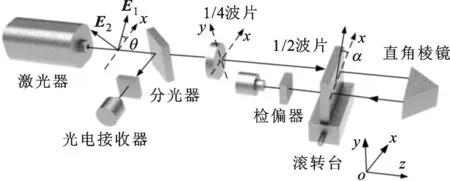
图1 测量原理光路图[5]

1.2 数学建模

建立如图1所示的坐标系,以1/4波片快轴为x轴,慢轴为y轴,正交线偏振光与x轴的夹角为θ,1/2波片快轴与x轴夹角为α,调节检偏器偏振方向与x轴重合,则可得光电探测器接收的测量光信号为[6]

E=[(cosθcos4α+isinθsin4α)E1+

(1)

式中:E1=A1e-i(2πf1t+φ1),E2=A2e-i(2πf2t+φ2),f1、f2分别是正交线偏振光矢量E1、E2的频率。

光电探测器接收到的测量光信号光强为

φ1-φ2+Ψ]

(2)

其中k1=(cos2θcos24α+sin2θsin24α)1/2

k2=(sin2θcos24α+cos2θsin24α)1/2

Ψ=arctan(tanθtan4α)+arctan(cotθtan4α)

同理,可得光电探测器接收到的参考光信号光强为

(3)

因此,可得测量信号和参考信号相位差为

ΔΨ=arctan(tanθtan4α)+arctan(cotθtan4α)

(4)

定义角度放大率为

(5)

式(4)给出了一般情况下的相移ΔΨ与1/2波片转角α的关系,图2给出了几组θ角下二者之间的关系。由图可得,在一些特殊点附近相位变化灵敏,在一定范围内保持了良好的线性关系。取一个特殊区域,即在α=0附近时,式(4)和式(5)可以近似为

ΔΨ=4(tanθ+cotθ)α

(6)

Kα=4(tanθ+cotθ)

(7)

从式(6)、(7)可得,当θ趋近于0时,Kα可以趋于无穷大,滚转角测量分辨率就越强,但此时测量信号光强就越弱,不利于信号处理。为既保证足够的角度放大率,又保证测量信号有足够的光强,通常情况下θ取2°[6],则Kα=114,相位计的分辨率为0.001°时,滚转角的分辨率理论上可以达到0.03″,完全满足数控机床1″的分辨率要求。

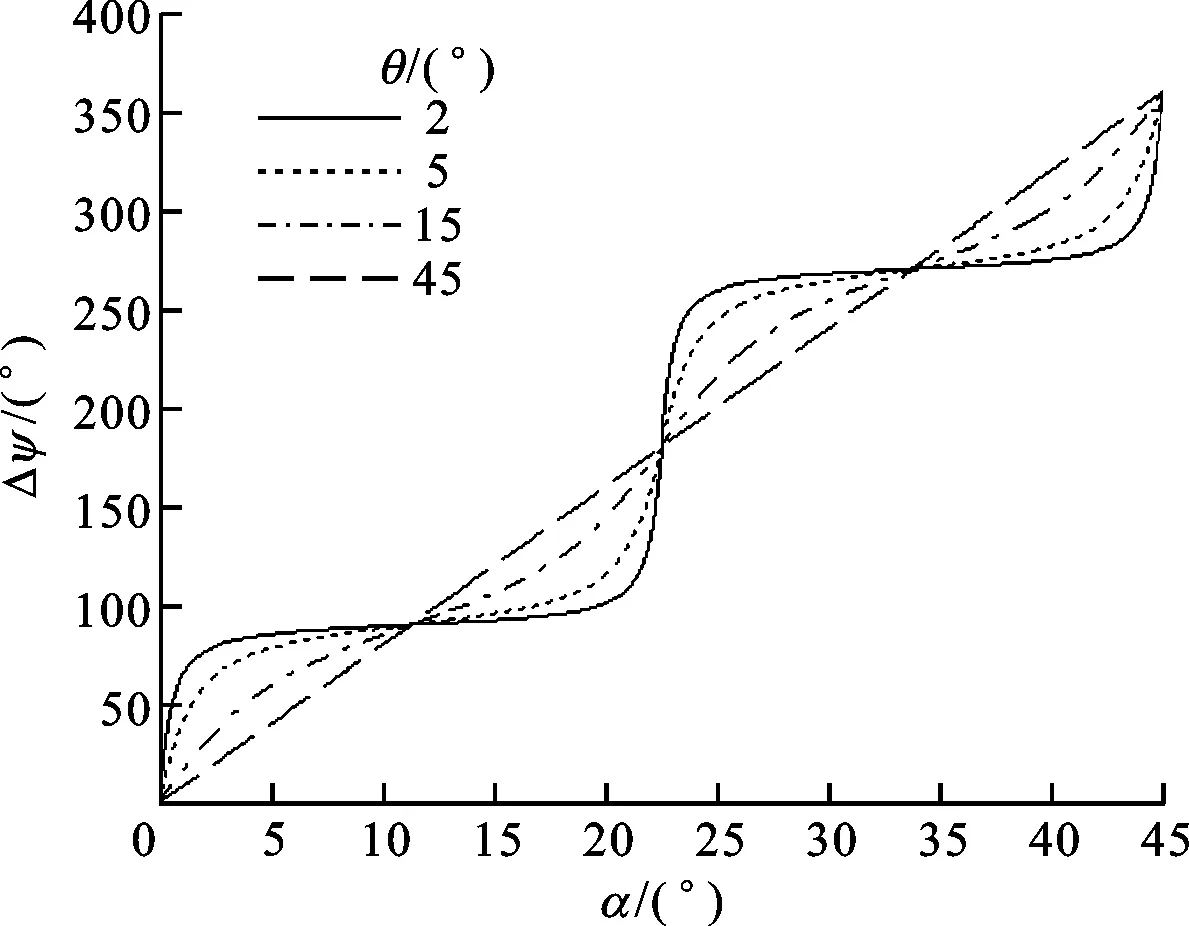
图2 ΔΨ与α的关系曲线

2 频偏引起相位误差分析

频偏即频率偏差,指测量信号和参考信号频率不相等,有偏差。在一般测量中,小的频偏的影响可以忽略不计,但是在高精度滚转角测量系统中,这种小的频偏会造成相位值的波动[7],从而对滚转角测量精度造成非常大的影响。本节分析了频偏产生的原因,以及用MATLAB仿真分析了其会产生滚转角测量误差,最后用实验数据证明了分析的正确性。

2.1 频偏的产生

式(2)、(3)分别是光电探测器接收的测量光光强和参考光光强,可以简化为

Is=I1+Ascos[2π(f1-f2)t+φ1-φ2+Ψ]

(8)

Ir=I2+Arcos[2π(f1-f2)t+φ1-φ2]

(9)

理论上,频差f1-f2是不变的,但实际上是变化的。实验室所用He-Ne双频激光器频差在1 min内的变化如图3所示,由图可得,频差的大小随时间周期性变化,变化趋势近似正弦,因此频差可以近似描述为

f1-f2=f0+A0sin(2πf3t+φ3)

(10)

式中:f3为f1-f2变化的频率;A0为f1-f2变化的幅值;f0为偏置;φ3为初始相位。

图3 双频激光器频差波动

另外,测量信号和参考信号在经过光电探测器之前是同步的,但由于光电探测器响应时间不同,两路信号经过光电探测器光电转换之后出现延迟,导致两路信号的频率出现小的偏差,即频偏。设两光电探测器的响应时间分别为t1和t2,则经过光电探测器滤去直流分量后,得到的测量信号和参考信号分别为

Es∝Ascos[2π(f1-f2)s(t-t1)+φ1-φ2+Ψ]

(11)

Er∝Arcos[2π(f1-f2)r(t-t2)+φ1-φ2]

(12)

其中,(f1-f2)r和(f1-f2)s分别为经过光电探测器后测量信号频率和参考信号频率,分别为

(f1-f2)s=f0+A0sin[2πf3(t-t1)+φ3]

(13)

(f1-f2)r=f0+A0sin[2πf3(t-t2)+φ3]

(14)

将式(13)、(14)分别代入式(11)、(12)中,计算测量信号和参考信号的相位差,化简得

ΔΨ=2πf0(t2-t1)+2πA0{sin[2πf3(t-t1)+φ3]-sin[2πf3(t-t2)+φ3]}t+2πA0{sin[2πf3(t-t2)+φ3]t2-sin[2πf3(t-t1)+φ3]t1}+Ψ

(15)

记Δt=t2-t1,Δf=A0{sin[2πf3(t-t1)-sin[2πf3(t-t2)+φ3]},Δf即是经过光电探测器后测量信号和参考信号的频偏量(f1-f2)s-(f1-f2)r。对于中低频差双频激光器,f1-f2变化幅度的量级一般为几千赫兹或者更高,光电探测器响应时间在纳秒级,则2πA0{sin[2πf3(t-t1)+φ3]t1-sin[2πf3(t-t2)+φ3]t2}远小于0.001°(本研究所用CH6000A相位计最小分辨率),所以该项可以忽略不计,因此两路信号相位差可简化为

ΔΨ=2πf0Δt+2πΔft+Ψ

(16)

当Δt=0时,则Δf=0,式(16)就化为式(4),即测量信号和参考信号相位差理论公式。

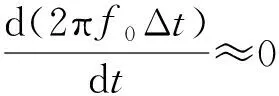
2.2 频偏引起的误差

频偏会导致相位差出现波动,进而引起滚转角的测量误差。由式(16)可得,频偏对相位的影响为2πΔft,转化为角度制即为360°Δft,实际上频偏往往是变化的,不是固定不变的,故频偏对相位的影响为

(17)

其中,由式(15)可得

Δf=(f1-f2)s-(f1-f2)r=

A0sin[2πf3(t-t1)+φ3]-

A0sin[2πf3(t-t2)+φ3]=

2A0sin(πf3Δt)cos(2πf3t-πf3(t1+t2)+φ3)≈

2πA0f3Δtcos(2πf3t-πf3(t1+t2)+φ3)

(18)

将式(18)代入式(17)中,得

ΔΨΔf(t)=360°A0Δtsin(2πf3t-

πf3(t1+t2)+φ3)

(19)

由式(10)、(18)、(19)可得,频偏Δf和相位差均余弦或者正弦变化,且与双频激光器频差f1-f2的变化周期相等。

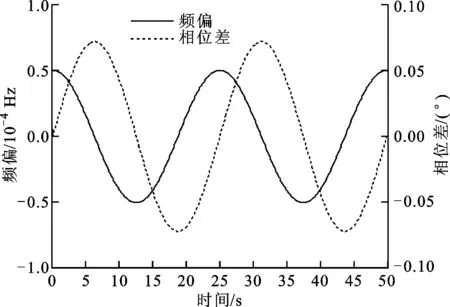
图4 频偏和相位差随时间的变化

频偏波动的幅值约为5×10-5Hz,其相位变化峰峰值为0.144°左右。按方案设计的Kα=114计算,其会引起滚转角4.5″的波动。对于数控机床滚转角高精度测量要求来说,4.5″的波动是不能满足精度要求的,因此必须减小或者消除频偏。

2.3 实验分析

对于如图1所示的测量系统,在1/2波片不转动的情况下,使用CH6000A相位计同时测量参考信号与测量信号的相位差和参考信号的频差,测量结果如图5所示。由于相位计CH6000A对频率测量的分辨率有限,无法分辨到10-6Hz,因此不能直接测得测量信号和参考信号之间的频偏。

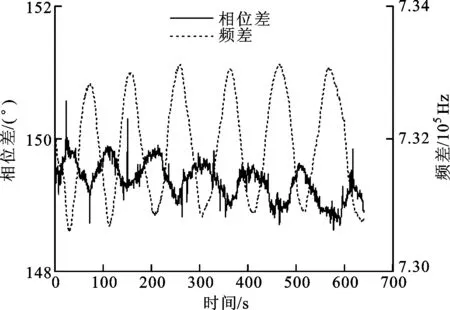
图5 相位差和频差随时间的变化

由图5可得,相位随频差同周期变化,且近似为正弦或者余弦变化,与数学模型仿真分析结果基本相符。不考虑突变的数据点时,相位差在一个周期内的平均变化量为0.7°,是仿真分析的4.87倍。这是由仿真分析的参数与实际参数的差异造成的,因为光电探测器由光电二极管及其后续放大电路等组成,较为复杂,并没有其响应时间的准确数值,200 ns只是一个估计值而已,与实际响应时间存在较大的偏差,因此实际相位变化与仿真分析结果有一定偏差是可以接受的。总体来说,实际实验结果与理论分析结果基本相符。

3 频偏的减小与消除

3.1 消除原理

由式(18)可得,频偏是由双频激光器频差的不稳定性和光电探测器的响应时间的不一致性共同作用导致的,因此可以通过提高双频激光器的稳频精度,即减小频差变化幅值A0和变化频率f3,以及提高光电探测器的一致性,即减小两光电探测器的响应时间差Δt来减小频偏。

频偏对相位差的影响见式(19),可得f3对相位差的波动幅度不产生影响,进而就不会对滚转角测量精度产生影响,因此在选择双频激光器时就可以放宽对f3的要求。

3.2 实验验证

实验室原先使用的光电探测器由成都工具研究所提供,10 min内相位差的波动情况如图5所示,平均每个周期的相位波动量为0.7°。将光电探测器更换为Δt更小的成都工具研究所的同一型号产品,则10 min内的相位差波动情况如图6所示。

图6 更换光电探测器后相位差和频差随时间的变化

由图6可得,更换Δt更小的光电探测器后,不考虑突变的数据点时,相位差在一个周期内的平均波动量为0.1°左右,低于之前0.7°的波动量,效果明显改善,从而验证了通过减小两光电探测器的响应时间差来降低频偏和相位差波动幅度的方法的可行性。

4 结 论

本文主要从理论上分析了基于相位的激光外差滚转角测量系统频偏产生的原因,以及频偏对于滚转角测量造成的误差影响,并进行了实验验证,结果表明微小的频偏会造成相位值的波动,进而对滚转角测量精度造成非常大的影响。针对该问题,文中提出通过提高双频激光器的稳频精度和减小光电探测器的响应时间差的方法来减小和消除频偏,降低相位差的变化幅度,进而提高滚转角测量精度,并通过实验证明了方法有效可行。

[1] CORONKEVICH P, TARASOV G G, HANO B A. Roll angle measurement with dual-frequency laser [J]. Automeasurement, 1974(1): 68-71.

[2] JIANG Hong, YIN Chunyong. Sensitivity enhanced roll angle measurement [J]. Optical Engineering, 2000, 39(2): 516-519.

[3] 柳忠尧, 林德教, 殷纯永, 等. 高精度滚转角干涉仪 [J]. 光学技术, 2002, 28(4): 332-336. LIU Zhongyao, LIN Dejiao, YIN Chunyong, et al. High precision roll angle interferometer [J]. Optical Technique, 2002, 28(4): 332-336.

[4] 王昭, 汤善治, 高建民, 等. 一种基于阵列式多次反射的滚转角测量装置及方法: 中国, CN102654392A [P]. 2012-09-05.

[5] 钟丽红, 王昭, 汤善治, 等. 机床滚转角测量中敏感元件倾斜引起的误差分析 [J]. 西安交通大学学报, 2013, 47(5): 99-103. ZHONG Lihong, WANG Zhao, TANG Shanzhi, et al. Measurement error analysis for machine tool roll error measurement due to inclined half wave plate [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 99-103.

[6] 汤善治. 基于激光外差干涉的数控机床几何精度测量理论与方法研究 [D]. 西安: 西安交通大学, 2013.

[7] 刘灿涛, 赵伟. 频偏对数字积分法测量相位差影响的研究 [J]. 电工技术学报, 2002, 17(3): 63-66. LIU Cantao, ZHAO Wei. Research for the effect of frequency windage to measuring phase difference with digital integral method [J]. Journal of Electric Technology, 2002, 17(3): 63-66.

(编辑 荆树蓉)

Analysis of Frequency Excursion in High-Precision Measurement of Machine Tool’s Roll Angle

YU Bao1,WANG Zhao1,HUANG Junhui1,QI Jingya2,LI Zhaohui2,GUO Junjie3

(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China;3. Shaanxi Hengtong Intelligent Machines Co.Ltd., Xi’an 710049, China)

In order to decrease the phase-different fluctuation and increase the roll angle measuring accuracy in extrapolation interference method, a new mathematical model of measurement optical path and reference optical path was established through Jones matrix method. The model takes the frequency unsteadiness of two-frequency laser and the difference of photo-detector’s response time into consideration based on the existing model and deduces that the frequency difference between the reference signal and measuring signal (frequency excursion) is the main cause of phase-different fluctuation. So it can be concluded that the frequency excursion is caused by the frequency unsteadiness of two-frequency laser and the difference of photo-detector’s response time. The effect of frequency excursion on the roll angle measuring accuracy is also calculated. Based on the model, this paper presents a method of increasing two-frequency laser frequency stabilization and decreasing the difference of photo-detector’s response time to eliminate phase-different fluctuation. Experimental results indicated that after decreasing the difference of photo-detector’s response time, the range of phase fluctuation was decreased from 7°to 1° and the roll angle measuring error decreased by 85.7%, which proves that the new model is feasible.

phase difference; roll angle; frequency excursion; precision

10.7652/xjtuxb201603016

2015-05-19。 作者简介:余宝(1990—),男,硕士生;王昭(通信作者),女,教授。 基金项目:国家自然科学基金青年基金资助项目(61405156)。

时间:2015-12-08

http:∥www.cnki.net/kcms/detail/61.1069.T.20151208.1640.006.html

TH741

:A

:0253-987X(2016)03-0101-05