刀具磨损图像视差图的非标定方法
2016-12-23朱爱斌何大勇邹超陈渭
朱爱斌,何大勇,邹超,陈渭
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
刀具磨损图像视差图的非标定方法
朱爱斌,何大勇,邹超,陈渭
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
刀具磨损检测的视场范围很小、现场工况复杂(存在机床护罩和刀具保持架的遮挡),而以往对摄像机进行标定的方法多用于大视场环境,并不适合于加工现场的刀具磨损检测。为此,文中提出一种采用非标定双目视觉方法获取刀具磨损图像视差图的方法,无需标定参考物和人工干预。首先,利用SURF(speeded-up robust features)算法检测图像对中的特征点;其次,利用8点算法计算基本矩阵,再利用极点无穷远变换完成图像对的校正;最后,利用基本区域匹配方法完成图像对视差的计算。进行了加工现场的磨损刀具图像获取实验,先对比了重构出的刀具视差图轮廓与实际轮廓,接着分析了刀具视差图的精度。结果显示,重构轮廓与实际轮廓基本相符,重构出的视差图的绝对误差在5个像素点以下,相对误差在10%至30%之间,说明在小视场和复杂工况下,用非标定方法获取的刀具视差图能够满足现场检测的精度要求,并且该方法具有灵活和高效的特点。
刀具磨损;视差图;非标定方法;双目视觉
在双目视觉中,视差是指空间一点在2幅图像中形成的2个成像点坐标上的差异。视差图是以原图为大小、以各个视差值为元素的图像。刀具磨损图像的视差图能够间接反映出刀具磨损表面的深度信息,对于刀具磨损表面的三维重构具有重要意义[1-2]。通过获取磨损表面的三维信息,可以对刀具磨损状态进行有效检测,从而减少机床故障的停机时间,提高自动化加工效率。对双目视觉中采用标定方式获得视差图的方法而言,需要标定摄像机以获得其内外参数,然后进行图像对校正和视差计算[3]。张铖伟等介绍了摄像机标定的基本方法和步骤,并比较了不同标定方法的特点[4]。Zhou等提出了一种改进的随机抽样一致算法,并借助标定板准确地计算出了摄像机的内外参数[5]。刘亚菲采用标定的双目视觉方法,对大型工件的焊接位置进行了测量[6]。王琳等采用张正友标定法对2个摄像机进行标定,计算出了桥梁裂缝的长度和宽度[7]。许薛军等采用基于Tsai标定法的双目视觉方法,对公路边坡位移进行了识别[8]。Wang等针对大视场视觉测量应用,提出了两步标定法用于计算摄像机参数[9]。但是,以上标定方法都是在大视场范围进行的,并且需要标定参考物和人工干预。考虑到刀具磨损检测的视场范围很小并且现场工况复杂(存在机床护罩和刀具保持架的遮挡),放置标定参考物很不方便,且加工时无法进行人工干预,所以标定的方法不适合加工现场的刀具磨损检测。
针对上述情况并结合现场刀具磨损检测的特点,本文提出采用非标定双目视觉方法获取刀具磨损图像的视差图,通过对比重构出的视差图轮廓与实际轮廓之间的差异来分析视差图的精度。结果显示,非标定方法能够适应小视场和复杂工况,具有灵活和高效的特点。
1 双目视觉方法基本原理
双目视觉方法可以理解为通过三维空间物体在左右2个摄像机成像平面上形成的数字图像,反推出三维空间物体点在世界坐标系中的坐标的过程。
在理想条件下,左右2个摄像机的成像平面平行,如图1所示,可以利用三角测距原理确定空间点P的深度值。点P的深度计算公式[10]为
(1)
式中:f为摄像机焦距;B为左右摄像机光心的基线距离;dx为视差。

图1 三角测距原理图
2 刀具磨损图像视差图获取算法
获取刀具磨损图像的视差图对重构出刀具磨损表面的深度信息具有重要意义。由前面的分析可知,要获取视差图必须先使左右成像平面平行,而实际情况下左右成像平面并不平行,如图2所示。
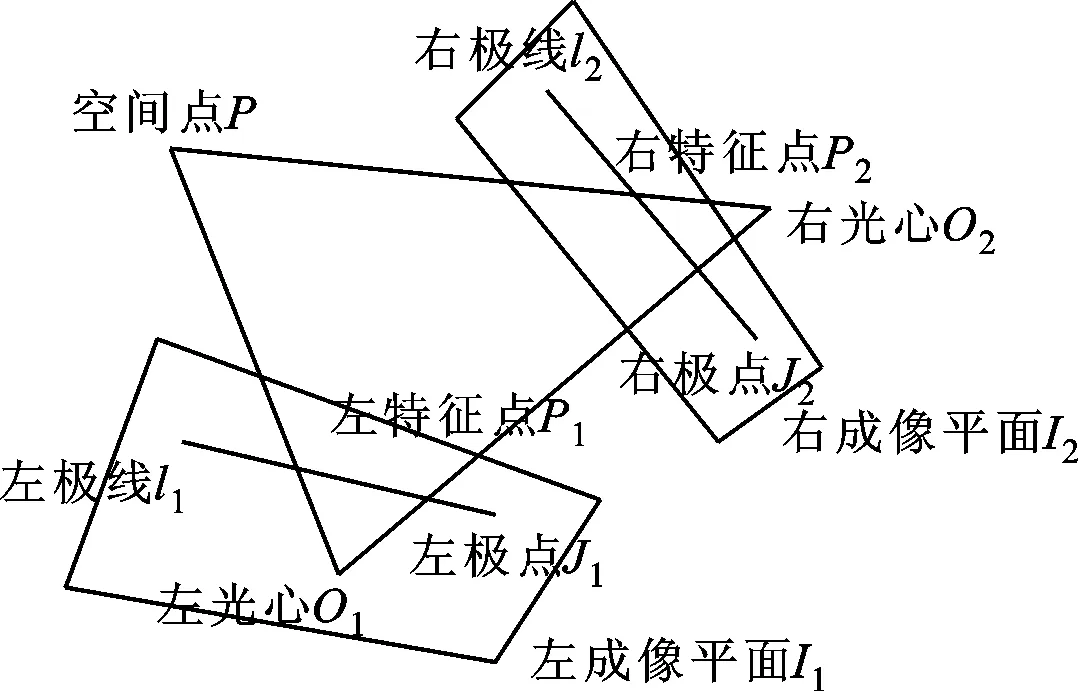
图2 空间一点成像示意图
因此,需要对左右成像平面进行校正,使得左右成像平面平行,这样才可以进行视差计算。可以采用标定参考物对摄像机进行标定,根据标定得到的摄像机内外参数对左右摄像头获取的图像进行校正[3]。但是,由于刀具磨损检测的视场范围很小,刀具磨损检测现场工况复杂,放置标定参考物很不方便,且加工时无法进行人工干预,所以利用标定方法进行校正的实用性较差。
本文提出采用非标定方法对左右2幅刀具磨损图像进行校正。在图2中,极线l1与l2在PO1O2三点构成的平面内,这个线面关系约束称为极线约束,在数学上用基本矩阵来表示极线约束。基本矩阵代表了左右2幅图像对应点之间的关系,通过基本矩阵对2个对应点之间的几何关系进行约束,可以使2幅图像的畸变最小。这种方法不需要进行标定,处理过程称为极线约束下的图像校正。
利用非标定双目视觉获取视差图的基本过程如如3所示。

图3 非标定双目视觉获取视差图过程
2.1 用SURF算法提取图像对特征点
SURF(speeded-up robust features)算法由Bay等提出[11],是一种尺度和旋转不变的检测子和描述子,用来检测图像中的特征点。
为了保证检测子和描述子的尺度不变性,需要在不同尺度下对图像进行特征点检测。SURF算法使用不同大小的方形滤波器与图像进行卷积,滤波器则通过高斯函数进行加权。SURF算法利用特征点的近似Hessian矩阵作为特征点的响应。对于尺度为σ、坐标为x=(x,y)的图像点,Hessian矩阵定义为
(2)
式中:Lxx为图像点处灰度值与高斯函数二阶导数的卷积;Lxy、Lyx和Lyy的含义与Lxx类似。高斯函数为
(3)
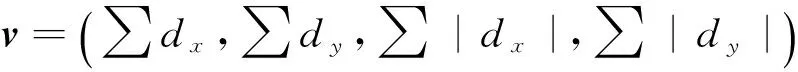
2.2 基本矩阵的计算
基本矩阵包含了图像对应匹配特征点的极线约束,建立了左右图像中对应点集的映射关系。假设矩阵F是图像对(I1,I2)的基本矩阵,P1=(x,y,1)T和P2=(x′,y′,1)T(齐次坐标)分别是2幅图像上对应的特征点,那么基本矩阵和2个特征点之间有如下关系[10]
(4)
另外,基本矩阵F和左、右极点J1、J2之间的关系[10]为
(5)
若将基本矩阵元素用f及下标表示,则式(4)变为
x′xf11+x′yf12+x′f13+y′xf21+
y′yf22+y′f23+xf31+yf32+f33=0
(6)
若有n个对应特征点,则式(6)可写成如下矩阵形式
Af=0
(7)
本文采用由Longuet-Higgins提出的8点算法[12],该算法只需要8个匹配的特征点即可求解出基本矩阵,运算速度快。
8点算法计算基本矩阵的流程如下。
(3)去坐标变换。基本矩阵F=t′TF′t,其中F为原来特征点对应的基本矩阵。
2.3 图像对校正
使左右2个成像平面完全平行的过程称为图像对的校正,如图4所示。

(a)校正前 (b)校正后图4 图像对校正原理
由图4可知,校正之后图像对的极点被映射到无穷远处,并且对应极线平行。问题转化为先计算左校正矩阵H将左极点映射到无穷远,再计算右校正矩阵H′将右极点映射到无穷远,同时要注意在计算H′时要满足校正后的图像畸变最小。
先计算左校正矩阵H。假设点u0位于原点,左极点J1=(m,0,1)T位于x轴,考虑如下变换
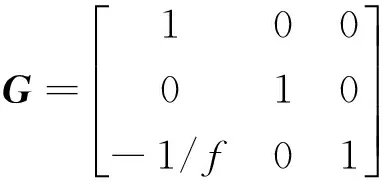
(8)
该变换将极点(m,0,1)T映射到无穷远点(m,0,0)T,而一个任意点(u,v,1)T在上述变换的映射下将变为(u,v,1)T=(u,v,1-u/f)T。
所以,对任意兴趣点u0和左极点J1,左校正变换可以表示为
H=GRT
(9)
式中:G将左极点J1变换到无穷远;R将左极点J1变换到x轴;T将兴趣点u0变换到原点。
再计算右校正矩阵H′,并保证校正后图像畸变最小。为保证图像畸变最小,采用如下判别标准[10]
(10)
另外,基本矩阵F可以表示成
F=[J2]×M
(11)
式中:[J2]×为右极点J2向量形成的反对称矩阵;M为非奇异矩阵。
用左校正矩阵H表示右校正矩阵H′
H=(I+H′J2aT)H′M
(12)
式中:a为特定向量。
由于H′将右极点J2映射到无穷远点(1,0,0)T,即H′J2=(1,0,0)T,那么有
(13)
从而有H=AH′M,即
H′=A-1HM-1
(14)
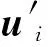
(15)
式(15)是一个线性最小二乘估计问题,利用线性方法就可以求解出未知参数a、b和c,从而得到A。至此,左右校正矩阵H和H′已全部求出。上述图像校正过程总结如下:
(1)得到基本矩阵,根据式(5)计算图像对的对应极点;
(2)计算图像对的左校正矩阵H;
(3)依据畸变最小原则,计算图像对的右校正矩阵H′;
(4)根据得到的2个校正矩阵分别对2幅图像做校正变换。
2.4 利用基本区域匹配算法的图像对匹配
校正后的图像对匹配点的横坐标相同,只需要在另外一幅图像中相同的横轴上搜寻对应的匹配点。这里利用基本区域匹配算法执行图像对的立体匹配。基本区域匹配是以图像中的点为中心构建一个固定大小的区域,以像素灰度平均绝对误差Ema为指标,计算一幅图像的某个区域内像素点的灰度值与另外一幅图像的相同横坐标轴上相同大小区域内像素点的像素灰度平均绝对误差[13]。在通常情况下,固定某一幅图像的一个点坐标之后,遍历另外一幅图像中相同横坐标的点,像素灰度平均绝对误差最小的点即为匹配点。像素灰度平均绝对误差定义如下
Ema(x,y)=

(16)
式中:模板半径i取为3;f(x,y)是(x,y)处的像素点灰度值。
3 加工现场刀具磨损图像获取实验
3.1 重构轮廓形状分析
为了在加工现场进行刀具磨损检测,采用微距摄像头,用磁性表座对摄像头进行固定。实验在G-CNC6135数控车床上进行,回刀时在车床上进行检测,刀具为45°YW2型硬质合金焊接车刀。使用自行开发的软件获取图像,实验装置如图5和图6所示。

图5 现场刀具磨损检测装置

图6 检测细节
首先,针对背景与结构关系简单、对比度低的问题对图像进行预处理;接着,使用SURF算法对图像特征点进行检测,得到大量的对应匹配点;然后,根据对应匹配点计算出基本矩阵,再经过极点无穷远变换得到校正后的图像对。过程如图7和图8所示,可以看出,校正后的图像畸变较小,并且相同位置图像特征点的横坐标相同。

(a)左图像特征点检测 (b)右图像特征点检测图7 SURF算法检测到的焊接车刀匹配点

(a)校正后的左图像 (b)校正后的右图像图8 校正后的焊接车刀左右图像对
最后,使用基本区域匹配方法获取焊接车刀视差图,结果如图9所示。

图9 刀具磨损图像视差图
下面,通过观察3个关键位置处的轮廓,对重构出的刀具磨损区域视差图进行轮廓形状分析。为了减少噪声,使用均值滤波模板对视差图做均值滤波处理。选取的特征位置为上下2个刀尖与刀刃中部,选取方式如图10所示。

(a)下刀尖特征点坐标
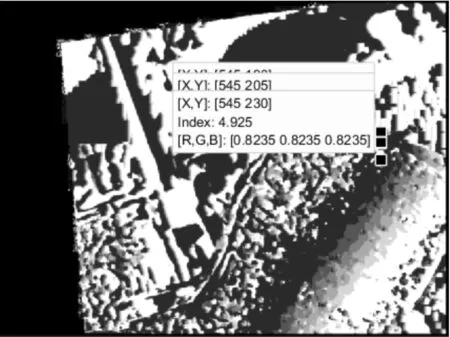
(b)刀刃特征点坐标图10 下刀尖与刀刃特征点坐标
图10a中,下刀尖特征点的坐标(坐标单位均为像素,下同)分别为(615,215)、(615,240)和(615,245),原点是左上角顶点,横轴为水平方向。图10b中,刀刃特征点坐标分别为(545,190)、(545,205)和(545,230)。类似地,选取上刀尖特征点坐标分别为(455,155)、(455,185)和(455,200)。选取这些点所在直线经过的各位置的视差值形成刀具磨损表面轮廓,如图11a~11c所示。
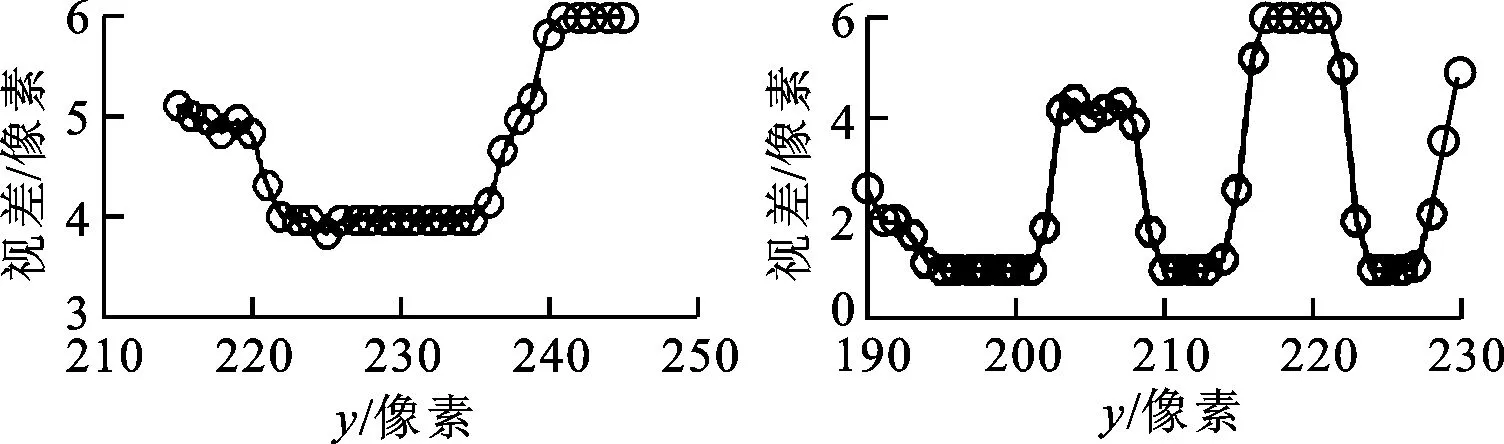
(a)下刀尖视差图轮廓 (b)刀刃视差图轮廓
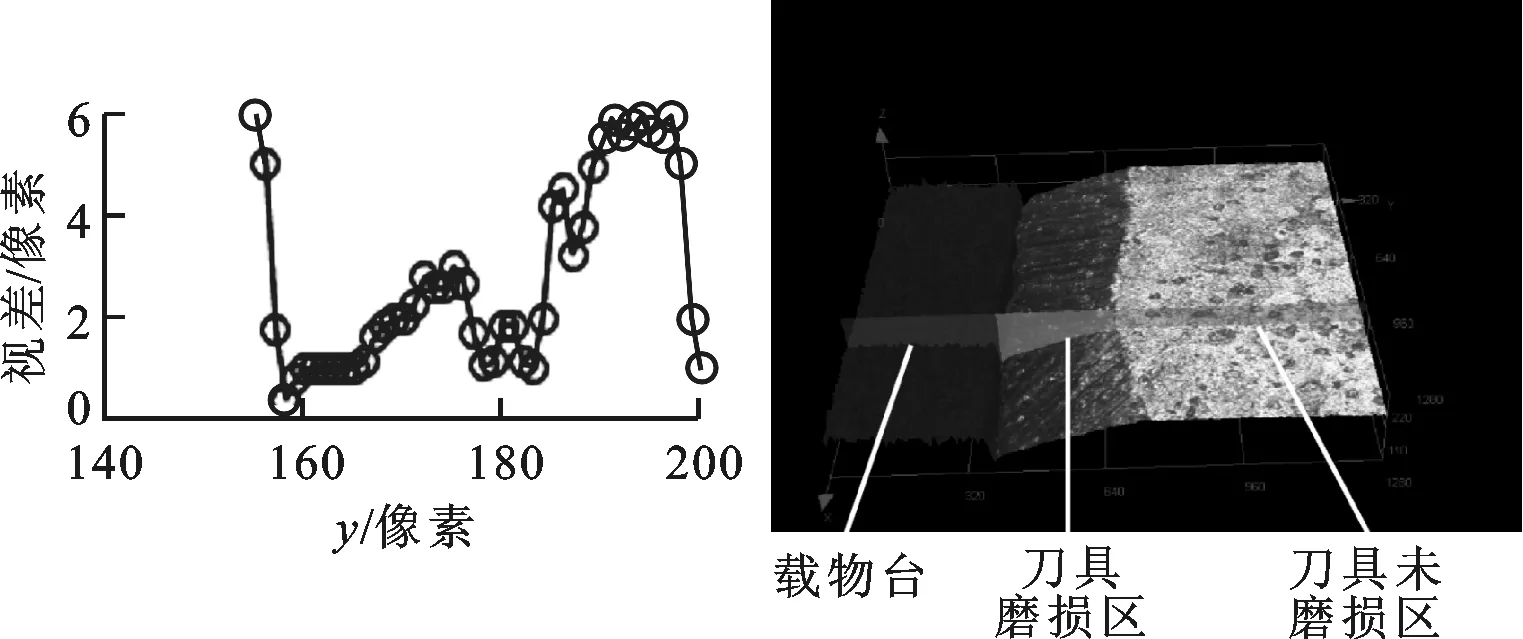
(c)上刀尖视差图轮廓 (d)显微镜下的轮廓图11 特征位置处视差图轮廓与显微镜下的轮廓
图11d是由奥林巴斯OLS4000共聚焦显微镜获得的刀具磨损表面轮廓形状,显微镜水平分辨率为0.12 μm,垂直分辨率为0.01 μm。可以看到,图中刀具磨损区域是一个斜坡。将图11a~11c分别与图11d作对比,发现重构出的视差图中磨损区域轮廓也呈斜坡状,与实际轮廓基本一致。
3.2 重构精度分析
由于图像校正过程可以近似认为是刚体变换,所以刀具表面的几何元素相对位置不发生改变,但由于校正后的图像是原图像的重采样,所以几何元素的长度与相对距离会发生改变。选取几何位置关系没有发生改变的刀具上下刀尖位置处的边界距离进行畸变系数计算,以减少校正过程产生的测量误差。如图12a所示,沿刀具前刀面的3个边界分别作3条直线相交于2点,分别为(319,115)与(525,227)。在图12b中,用相似方法求得2个交点的坐标为(326,288)和(614,407)。

(a)原图特征线段

(b)视差图特征线段图12 视差图相对原图的畸变系数计算
计算图12a与图12b中所取线段的长度,将两者的比值作为后面磨损区域宽度测量中的畸变系数[14]。计算结果:原图特征线段长度为234.48像素;视差图特征线段长度为311.62像素;线性畸变系数为1.33。
接下来进行视差图磨损区域测量宽度的精度分析。选取测量的第一个特征磨损区域为刀刃。为测量刀刃最小磨损宽度值,按图13a所示方法做3条直线交于2点,坐标分别为(527,225)和(523,233)。类似地,图13b中2点的坐标分别为(412,139)和(418,126)。

(b)视差图中的磨损宽度图13 刀刃最小磨损宽度测量

(a)原图中的磨损宽度

(b)视差图中的磨损宽度图14 刀尖特征位置一的磨损宽度测量
选取测量的第二个和第三个特征磨损区域为上刀尖处的2个凸点。在图14a中,过上刀尖磨损外边界作一条直线,向磨损内边界推移此直线直到与磨损内边界相接触,前刀面左边界与上述直线交于一点,即所求凸点,过此凸点作直线的垂线,该垂线段即代表磨损区域宽度。图14a中所取点的坐标为(303,138)和(307,162),图14b中所取点的坐标为(399,159)和(407,195)。
在图15中,用类似方法求取垂线段。图15a中所取点的坐标为(355,134)和(358,157),图15b中所取点的坐标为(468,150)和(473,178)。

(a)原图中的磨损宽度

(b)视差图中的磨损宽度图15 刀尖特征位置二的磨损宽度测量
根据上述坐标,计算所需测量处磨损区域的宽度,并将畸变校正后原图中的磨损区域宽度值与视差图得到的磨损区域宽度值进行对比,3个磨损区域的宽度值对比结果见表1。

表1 刀具特征位置磨损区域检测宽度的
w0:原图磨损区域宽度;w1:畸变系数校正后原图磨损区域宽度;w2:视差图磨损区域宽度;Eabs:绝对误差;δ:相对误差。
分析表1的数据可以发现,测量得到的磨损区域宽度绝对误差在5像素以下,相对误差在10%至30%之间。
综合上述重构出的视差图的轮廓分析与精度分析结果,发现重构出的视差图中的刀具轮廓与实际刀具轮廓形状基本相符,且重构出的磨损区域宽度的绝对误差在5像素以下,相对误差在10%至30%之间,表明采用非标定方法获取的刀具磨损图像的视差图基本能够满足加工现场的刀具磨损检测要求,且具有灵活和高效的特点。
4 结 论
本文提出了一种采用非标定双目视觉方法获取刀具磨损图像视差图的方法,无需获取摄像机的内外参数,无需标定参考物和人工干预即可完成图像对的校正和视差图获取。分析表明:采用本文方法重构出的刀具视差图轮廓与实际轮廓基本相符;分析视差图测量得到的磨损区域宽度与原图测量得到的磨损区域宽度,可知现场加工环境中非标定双目视觉方法的测量精度可以达到5像素以下,相对误差在10%至30%之间。造成误差的因素涉及摄像头像素及感光性能、现场光源条件、车床的轻微振动、视差图获取算法等,未来可通过采用更高质量的摄像头、设置附加光源、完善图像处理算法等途径来提高精度。
本文的研究表明,非标定双目视觉方法无需对摄像机进行标定,能够在复杂工况下获取刀具磨损图像的视差图,且视差图的精度基本能够满足加工现场刀具磨损检测的要求,具有灵活和高效的特点。未来的工作重点将放在提高刀具磨损图像视差图的精度方面。
[1] CERCE L, PUSAVEC F, KOPAC J. 3D cutting tool-wear monitoring in the process [J]. Journal of Mechanical Science and Technology, 2015, 29(9): 3885-3895.
[2] WANG Z, LI B, ZHOU Y. Fast 3D reconstruction of tool wear based on monocular vision and multi-color structured light illuminator [C]∥Proceedings of International Symposium on Optoelectronic Technology and Application. Bellingham, WA, USA: SPIE, 2014: 93011D.
[3] FORSYTH D, PONCE J. Computer vision: a modern approach [M]. 2nd ed. New York, USA: Pearson, 2011: 32-43.
[4] 张铖伟, 王彪, 徐贵力. 摄像机标定方法研究 [J]. 计算机技术与发展, 2010, 20(11): 174-179. ZHANG Chengwei, WANG Biao, XU Guili. Research of camera calibration methods [J]. Computer Technology and Development, 2000, 20(11): 174-179.
[5] ZHOU F, CUI Y, WANG Y, et al. Accurate and robust estimation of camera parameters using RANSAC [J]. Optics and Lasers in Engineering, 2013, 51(3): 197-212.
[6] 刘亚菲. 大型工件焊接双目视觉测量及精度研究 [D]. 上海: 华东理工大学, 2013.
[7] 王琳, 赵健康, 夏轩, 等. 基于双目立体视觉技术的桥梁裂缝测量系统 [J]. 计算机应用, 2015, 35(3): 901-904. WANG Lin, ZHAO Jiankang, XIA Xuan, et al. Bridge crack measurement system based on binocular stereo vision technology [J]. Journal of Computer Applications, 2015, 35(3): 901-904.
[8] 许薛军, 张肖宇. 基于双目视觉的公路边坡表面位移识别方法 [J]. 中国公路学报, 2015, 28(4): 27-34. XU Xuejun, ZHANG Xiaoyu. Highway slope displacement identification method based on binocular vision [J]. China Journal of Highway and Transport, 2015, 28(4): 27-34.
[9] WANG Z, WU Z, ZHEN X, et al. A two-step calibration method of a large FOV binocular stereovision sensor for onsite measurement [J]. Measurement, 2015, 62(2): 15-24.
[10]HARTLEY R, ZISSERMAN A. Multiple view geometry in computer vision [M]. 2nd ed. Cambrige, England, UK: Cambridge University Press, 2004: 295-305.
[11]BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF) [J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359.
[12]LONGUET-HIGGINS H C. A computer algorithm for reconstructing a scene from two projections [J]. Nature, 1981, 293(36): 133-135.
[13]HASSEN W, AMIRI H. Block matching algorithms for motion estimation [C]∥Proceedings of IEEE International Conference on e-Learning in Industrial Electronics. Piscataway, NJ, USA: IEEE, 2013: 136-139.
[14]胡浩强. 基于不完整信息图像融合的刀具磨损检测技术研究 [D]. 西安: 西安交通大学, 2015.
[本刊相关文献链接]
张鹏,陈湘军,阮雅端,等.采用稀疏SIFT特征的车型识别方法.2015,49(12):137-143.[doi:10.7652/xjtuxb201512 022]
崔汪莉,卫军胡,纪鹏,等.基于加权局部梯度直方图的头部三维姿态估计.2015,49(11):71-76.[doi:10.7652/xjtuxb 201511012]
周远,周玉生,刘权,等.一种适用于图像拼接的DSIFT算法研究.2015,49(9):84-90.[doi:10.7652/xjtuxb201509015]
刘凯,张立民,孙永威,等.利用深度玻尔兹曼机与典型相关分析的自动图像标注算法.2015,49(6):33-38.[doi:10.7652/xjtuxb201506006]
朱爱斌,胡浩强,何大勇,等.采用频域融合方法的砂轮刀具磨损三维重构技术.2015,49(5):82-86.[doi:10.7652/xjtuxb201505013]
郝雯洁,齐春.一种鲁棒的稀疏信号重构算法.2015,49(4):98-103.[doi:10.7652/xjtuxb201504016]
范优飞,胡红利,杨帆,等.一种48电极可配置电容层析成像系统模型.2015,49(4):110-115.[doi:10.7652/xjtuxb2015 04018]
唐晓庆,范赐恩,刘鑫.基于边缘保持滤波的单幅图像快速去雾.2015,49(3):143-150.[doi:10.7652/xjtuxb201503022]
刘天良,郑海红,罗圣美,等.改进的混合动静态背景的分割方法.2015,49(2):25-30.[doi:10.7652/xjtuxb201502005]
李鹏,杨旸,方涛.应用视觉显著性的快速有偏聚类超像素算法.2015,49(1):112-117.[doi:10.7652/xjtuxb201501019]
杨晔,潘希德,庄健.一种针对超声检测图像的自适应阈值设置方法.2015,49(1):127-132.[doi:10.7652/xjtuxb201501 021]
陈倩倩,张磊,徐刚,等.利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法.2014,48(12):100-106.[doi:10.7652/xjtuxb201412016]
侯兴松,张兰.方向提升小波变换域稀疏滤波的自然图像贝叶斯压缩感知.2014,48(10):15-21.[doi:10.7652/xjtuxb 201410003]
李博,冯松,毛军红.在线图像可视铁谱LED阵列反射光源设计与实现.2014,48(10):29-34.[doi:10.7652/xjtuxb2014 10005]
(编辑 葛赵青)
Uncalibrated Method for Disparity Map of Tool Wear Images
ZHU Aibin,HE Dayong,ZOU Chao,CHEN Wei
(Key Laboratory of Education Ministry for Modern Design & Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China)
The field of view of tool wear detection is small, and the site condition is complex (e.g., the blocking of machine cover and tool holder exists). Whereas the traditional method that needs camera calibration is mostly used in large field of view, which is not suitable for on-site tool wear detection. An uncalibrated method based on binocular vision is proposed in this paper for obtaining the disparity map of tool wear images without calibration reference or man-induced intervention. Firstly, SURF (speeded-up robust features) algorithm is used to detect the images’ feature points. Then, the 8-point algorithm is adopted to estimate the fundamental matrix; next, image correction is completed by pole infinity transform. Finally, the disparity map is obtained by basic block matching algorithm. On-site experiments were conducted to obtain the tool wear images, and the analysis on profile and accuracy of the reconstructed disparity map was performed. The results show that the reconstructed profile is basically consistent with the actual profile; the absolute error of the reconstructed disparity map is less than 5 pixels and the relative error is between 10% and 30%, meaning that the disparity map obtained by the uncalibrated method in small field of view and complex site condition can meet the accuracy requirement for on-site detection, and this method is also flexible and effective.
tool wear; disparity map; uncalibrated method; binocular vision
10.7652/xjtuxb201603002
2015-09-18。 作者简介:朱爱斌(1975—),男,副教授。 基金项目:国家自然科学基金资助项目(51175409)。
时间:2015-12-31
http:∥www.cnki.net/kcms/detail/61.1069.T.20151231.1129.004.html
TH113.2
:A
:0253-987X(2016)03-0008-08
