单个微凸体接触过程中的闪点温度研究
2016-12-23刘雨薇张卫正叶福浩
刘雨薇,张卫正,叶福浩
(1.中国矿业大学(北京)机电与信息工程学院,100083,北京;2.北京理工大学机械与车辆学院,100081,北京;3.北京奔驰汽车有限公司,100176,北京)
单个微凸体接触过程中的闪点温度研究
刘雨薇1,张卫正2,叶福浩3
(1.中国矿业大学(北京)机电与信息工程学院,100083,北京;2.北京理工大学机械与车辆学院,100081,北京;3.北京奔驰汽车有限公司,100176,北京)
为了对滑动摩擦副表面的闪点温度进行有效评估,以相对滑动粗糙表面上的单个微凸体间的瞬态接触导热过程为研究对象,假设两个粗糙表面上各自有一个微凸体发生接触,理论分析了滑动速度、最大贯穿深度、摩擦系数以及材料的热物性参数等因素对闪点温度的影响。研究表明,接触面中心位置处的闪点温度随着接触时间的延长而升高,在总的接触时长的82.5%时刻,闪点温度达到最大值,之后随着接触时间的延长,闪点温度逐渐降低,最大闪点温度比Archard模型的预测结果高10%。此外,最大闪点温度与滑动速度的平方根、最大贯穿深度的3/4次方、摩擦系数以及复合杨氏模量成正比,与热导率、密度和比热容的乘积成反比。该研究结果为后续滑动摩擦副摩擦磨损机理的研究奠定了理论基础。
滑动粗糙面;微凸体接触;闪点温度
具有粗糙表面的两个物体相接触时,由微凸体接触形成的实际接触面积是不连续的,并且远小于名义接触面积。当两物体之间发生相对滑动时,克服摩擦阻力产生的热量将首先通过发生接触的微凸体向内扩散,使得微凸体温升比摩擦表面的平均温度的温升高许多倍,从而对接触面产生有害的影响,导致金属表面的氧化速度加快,硬度降低,发生黏着的可能性增大,因而磨损率增大,甚至在较大的成块面积上形成黏着焊连。接触面上的最高温度又称闪点温度,闪点温度对接触表面的摩擦和磨损特性具有重要影响。
对于摩擦副闪点温度的研究已经有很多年的历史,最早对滑动摩擦系统中摩擦副表面温度进行计算的模型均假设几何接触面积足够大以保证稳定导热状态成立。如果一个表面是光滑的,或者硬度较高、较粗糙的表面在较软、较光滑的表面上滑动时,则该假设是合理的;若硬度和粗糙度相差不多的两个表面上的微凸体间的相互作用是瞬态的,持续的时间极短,则无法满足稳定导热状态成立。Ling等介绍了一种热量在时间和空间随机分布的情况下,计算滑动物块的接触表面温升的统计模型[1],发现表面温度是波动的,并且接触点的温度要比名义接触面的温度高很多。Archard建立了一个带有突起的物体在另一个物体表面滑动时的闪点温度模型[2],认为突起上的热源是相对静止的,相接触平面上的热源是移动的,并且对不同Peclet数下接触面上的平均闪点温度进行了计算。Kennedy用有限元方法对滑动系统中的闪点温度进行了预测[3],并与实验结果相吻合。
上述在对滑动摩擦副的闪点温度进行研究的过程中,模型所采用的接触轮廓与Archard模型相类似,滑动过程中接触面积始终保持不变,并且热流密度是均匀分布的。本文所研究的两个相互滑动的微凸体间接触面积大小随着接触时间发生变化,热流密度也随着接触压强的变化而改变。通过对接触过程中的瞬态导热情况进行分析,得到接触面中心位置处的闪点温度随接触时间的变化趋势,将最大闪点温度与Archard模型中的闪点温度相比较,探讨了材料特性参数对最大闪点温度的影响。
1 单个微凸体接触过程中的闪点温度
1.1 单个微凸体间瞬态接触过程中的导热分析
本文在GW模型[4]的基础上,假设每个粗糙表面上分布有不同高度的球形微凸体。当一个微凸体通过另一个微凸体时,两者之间经历了极短的接触作用,微凸体间典型的机械和热相互作用是一个瞬态过程。
粗糙表面通过单个微凸体模型进行描述时,微凸体实际接触区域中的作用力在原子与原子间作用力的范围内,因此可以假设这些区域中的温度是连续分布的。典型的微凸体之间的相对滑动速度很大,相互作用持续的时间非常短,因此可以将两个相互接触的物体的本体温度看作是常数,令T1=T2=0,并且热流的传递集中在垂直接触面的法线方向上,平行于接触面的横向热流忽略不计[5],从而将问题简化为与单个空间坐标和时间相关的导热问题。

(1)
(2)
(3)
式中:Ci=Ki/ki1/2,Ki为导热系数,ki为热扩散率,i=1,2分别表示物体1和物体2。
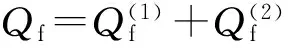
(4)
上述结论在滑动速度很大、微凸体相互作用时间很短的条件下是合理的。当滑动速度很小时,将会出现热稳定状态,摩擦生热量的分配比例等于两物体热导率的比值,即K1/K2[7]。
根据式(4)可知,物体1和物体2接触面上的单位面积热流率为
(5)
式中:q(x,τ)为单位面积上的摩擦生热率,等于单位面积上的摩擦力在单位时间内所做的功,即
q(x,τ)=μp(x,τ)V
(6)
在满足弹性接触的前提下,接触面积的半径a、法向接触力P、接触压强的分布p(r)可以根据赫兹接触理论[8]表示为
(7)
式中:R*为物体1和物体2粗糙表面上相互作用的两个微凸体峰顶的复合半径;E*为复合弹性模量;d为两个微凸体相互接触过程中的最大贯穿深度[9]。单个微凸体的接触是一个瞬态的接触过程,在给定的某个分离距离h0下,两个微凸体从开始发生接触直至分离的过程中,P不断地波动,最大贯穿深度d也不断发生变化,二者均随着接触时间先增大后减小;在初始时刻,P和d取得最大值,即有
(8)
(9)
式中:R1、R2为两个粗糙表面上的单个微凸体的半径;h1、h2为相对于各自参考平面的高度;b为两个微凸体峰顶间的空间最短距离;h0为两个表面参考平面间的距离;t0为接触作用的持续时间。
对单个微凸体在接触过程中的接触面积的运动形式进行简化,不考虑接触面积的移动,大小随着接触时间的增大先增大后减小,这将使得接触面积的中心始终处于被加热状态,因而最大温度将会出现在该中心位置(r=0)处。结合式(7)~(9),可得中心位置处的接触压强
(10)
将式(10)代入式(6),得到中心位置处的总的摩擦生热率
(11)
1.2 单个微凸体接触过程中的闪点温度
对于接触面上(x=0)单位时间内单位面积上的热流密度为f(t)的导热问题,Carslaw给出了t时刻距离接触面距离为x处的温度[5]
(12)
单个微凸体接触面上中心位置的坐标为x=y=0,则上式中对应的指数项等于1,并且单位时间内单位面积上的热流密度可由式(11)确定。对式(12)进行变量替换可以得到从开始接触到某一时刻t,接触面上中心位置处的瞬态温度为
(13)
结合式(5)、(11)、(13),可得接触面积中心位置的温度
(14)

(15)

图1 单个微凸体接触过程中接触面中心的变化趋势
1.3 闪点温度比较验证
Archard在对闪点温度进行计算时,假设接触面积为圆形,接触圆内的热流密度均匀分布,且在较大的滑动速度下的表面温度与距离接触面前缘的距离z的平方根成正比,即
T=Az1/2
(16)
式中:A为比例系数。对于接触半径为a的接触面,最高温度将出现在接触面的尾缘处,即
(17)
Archard模型中接触面积的轮廓如图2所示,接触过程中的平均温度可表示为
(18)
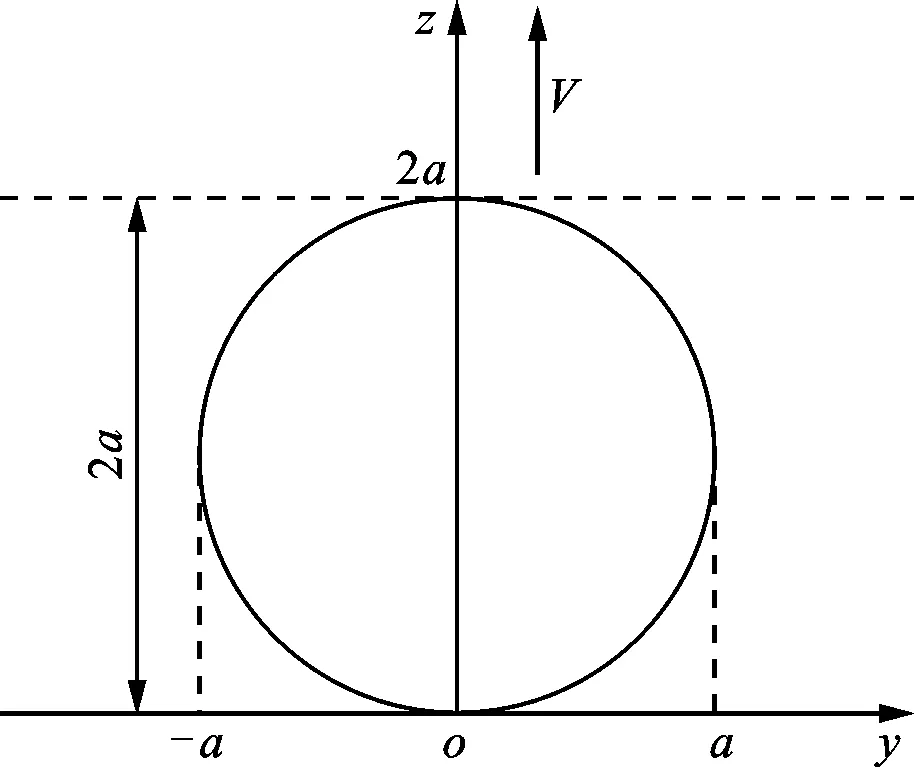
图2 接触面积的轮廓示意图
利用Maple对式(17)、(18)进行计算,可得粗糙表面上的最大温度与平均温度的比值
(19)
对于滑动速度较大的导热问题,Archard给出的平均温度为[2]
(20)
对于完全相同的两个表面,赫兹接触模型中接触面积的半径、法向接触力可化简为
(21)
将式(21)代入式(20),可得平均温度
(22)
将式(22)代入式(19),得到接触面上的最大温度
(23)
令式(15)中的R1=R2=R,C1=C2=C,可得两个完全相同的微凸体相互接触过程中的最高温度为
(24)
2 最大闪点温度的影响因素
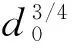
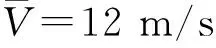
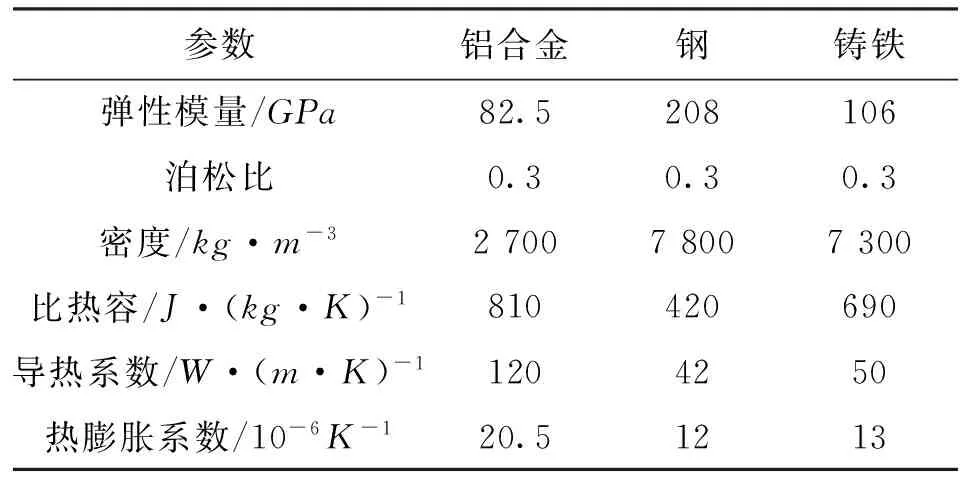
表1 活塞和气缸的材料参数
3 结 论
本文对具有相对滑动粗糙表面上的单个微凸体,在相互接触过程中产生的闪点温度的变化趋势及影响因素进行了分析研究,得到以下结论。
(1)接触面中心位置处的闪点温度随着接触时间的延长而升高,在总接触时间的82.5%时刻,闪点温度达到最大值,之后随着接触时间的延长,闪点温度逐渐降低。
(2)本文预测的单个微凸体接触过程中的最高温度比Archard预测的高10%。
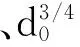
(4)在微凸体的峰顶半径和最大干涉深度一定的情况下,对于相同的滑动速度,以铝合金和铸铁为材料的单个微凸体,在接触过程中的最高温度低于以钢和铸铁为材料的单个微凸体接触的最高温度。
[1] LING F F, PU S L. Probable interface temperatures of solids in sliding contact [J]. Wear, 1964, 7(1): 23-34.
[2] ARCHARD J F. The temperature of rubbing surfaces [J]. Wear, 1959, 2(6): 438-455.
[3] KENNEDY F E. Surface temperatures in sliding systems: a finite element analysis [J]. Journal of Tribology, 1981, 103(1): 90-96.
[4] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal Society of London: Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319.
[5] CARSLAW H S, JAEGER J C. Conduction of heat in solids [M]. Oxford, UK: Clarendon Press, 1959.
[6] BERGMAN T L, INCROPERA F P. Fundamentals of heat and mass transfer [M]. [s.l.]: John Wiley & Sons, 2011.
[7] WANG S, KOMVOPOULOS K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part I Elastic contact and heat transfer analysis [J]. Journal of Tribology, 1994, 116(4): 812-822.
[8] JOHNSON K L, JOHNSON K L. Contact mechanics [M]. Cambridge, UK: Cambridge University Press, 1987.
[9] LIU Y, BARBER J R. Transient heat conduction between rough sliding surfaces [J]. Tribology Letters, 2014, 55(1): 23-33.
(编辑 赵炜 苗凌)
Research on the Flash Temperature in Single Asperity Contact
LIU Yuwei1,ZHANG Weizheng2,YE Fuhao3
(1. School of Mechanical Electronic & Information Engineering, China University of Mining & Technology, Beijing100083, China; 2. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;3. Beijing Benz Automotive Co., Ltd., Beijing 100176, China)
In order to estimate the flash temperature of sliding friction pair, the transient heat conduction between a single asperity contact on the rough sliding surfaces was investigated. Based on the assumption that there is only one asperity contact on each rough surface, the influences of sliding velocity, maximum interference, frictional coefficient, thermal-physical properties of the contacting materials on the flash temperature were analyzed. The results revealed that the flash temperature increased firstly and then decreased with the increase of contact time. The maximum value of flash temperature appeared at the moment when the contact time was about 82.5% of the total time, and it was 10% higher than that of Archard’s model. In addition, the flash temperature was in proportion to such factors as the square root of the sliding speed, the 3/4 power of the maximum interference, frictional coefficient, and compound elastic modulus, and inversely proportional to the thermal conductivity, and the product of density and specific heat capacity. These results provided a theoretical foundation for further study on the friction and wear mechanism of sliding friction pairs.
sliding rough surfaces; asperity contact; flash temperature
10.7652/xjtuxb201603014
2015-08-27。 作者简介:刘雨薇(1987—),女,博士,讲师。 基金项目:国家重点基础研究发展计划资助项目(613570303)。
TH117
:A
:0253-987X(2016)03-0090-05
