新型直旋混合射流破岩特性及机理分析

杜鹏,卢义玉,汤积仁,周哲,章文峰

(1.重庆大学煤矿灾害动力学与控制国家重点实验室,400030,重庆;2.重庆大学复杂煤气层瓦斯抽采国家地方联合工程实验室,400030,重庆)



新型直旋混合射流破岩特性及机理分析

杜鹏1,2,卢义玉1,2,汤积仁1,2,周哲1,2,章文峰1,2

(1.重庆大学煤矿灾害动力学与控制国家重点实验室,400030,重庆;2.重庆大学复杂煤气层瓦斯抽采国家地方联合工程实验室,400030,重庆)

为了揭示直旋混合射流的破岩机理,开展了直射流、旋转射流与直旋混合射流的冲蚀实验,并利用3DPIV测试系统获得了3种射流的速度场,通过对比分析相同靶距下冲孔深度及射流速度沿径向的分布规律,揭示了直旋混合射流的损伤破岩特性。结果表明,直旋混合射流可消除旋转射流的中心低速区和冲孔的中心凸台,该射流沿径向的分布宽度和破岩直径大于直射流,射流结构可分为直射流区、强旋射流区、弱旋射流区和外围射流区。直射流区的冲击破岩能力主要取决于射流能量;强旋射流区具有较大的径向和切向速度,当对岩石施加径向张力和周向剪力且在其合速度小于直射流的情况下,该区破岩深度仍可达到直射流区破岩深度;在弱旋射流区,受直射流和强旋射流的共同作用,岩石强度降低,但当三向速度均较小时亦能有效破岩;外围射流区主要是通过返回流携带岩屑对孔壁起磨削作用。

径向钻井;直旋混合射流;破岩机理;流场

用钻井方法开发低渗油气藏、页岩气和煤层气,是油气资源钻探发展的重要方向[1-3]。水力射径向钻井技术是首先利用磨铣钻头在套管和水泥环上开孔,然后利用自进式射流钻头带动高压软管沿径向钻出一定长度的孔,重复该步骤可在某一层位或多个层位钻出多个辐射状的井眼,进而提高油气采收率和产量[4-6]。

研究资料表明,目前用于水力破岩的射流形式主要有3种:普通直射流、旋转射流和组合射流[7-8]。李根生等发明了一种组合射流钻头,即双射流钻头[9],其结合了直射流和旋转射流的特性,但该钻头在高速流体的连续冲击下容易产生磨损甚至破坏,可靠性较低。

Buckman等设计了一种新型直旋混合射流钻头[10],能在岩石上钻出较大直径和深度的孔眼,符合径向钻井技术对钻孔的要求。Ma等针对直旋混合射流钻头实验研究了泵压、喷距和钻头结构参数等因素对钻孔特性的影响[11]。Liao等实验研究了不同射流形式下的钻头钻孔深度和直径,但没有具体分析冲孔孔底形状等特性[12]。从目前的研究来看,还没有学者结合直旋混合射流的流场特性和成孔特性得到冲击破碎岩石的机理。

本文通过冲蚀实验得到直旋混合射流的冲孔特性(直径、深度和孔底形状),并与旋转射流、直射流进行了对比分析,然后通过3DPIV测试系统得到射流的流场特性,由此阐述射流流场与成孔特性之间的关系,最后通过分析某一喷距下射流的速度分布规律和相应靶距的射流冲孔特性,结合已有的射流破岩理论,揭示了直旋混合射流的破碎岩石机理。

1 直旋混合射流钻头结构与原理

图1为自进式直旋混合射流钻头结构,其工作原理为:高压流体经过高压软管进入钻头后,一部分通过叶轮中心孔形成直射流,另一部分通过具有一定倾角的叶轮槽形成旋转射流,两股射流在混合腔内混合,最终由前喷嘴喷出,形成直旋混合射流;后喷嘴喷出的射流提供钻头和软管前进的动力。旋转射流流动轨迹类似于螺旋线,该流体质点具有三维速度,包括与射流轴心线平行的轴向速度u,与轴向速度垂直的径向速度v,与轴向、径向速度相垂直且与螺旋线相切的切向速度w[7],而轴心线附近的直射流主要为轴向速度u,如图2所示。

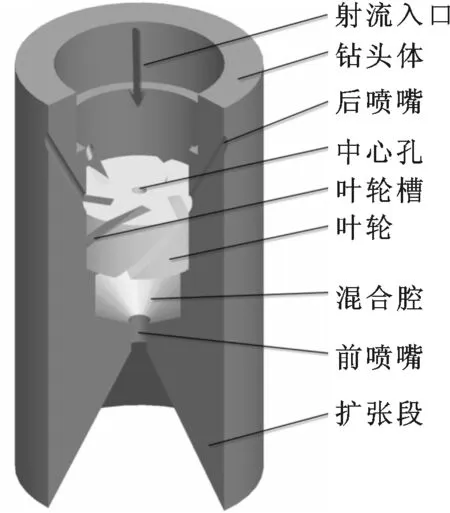
图1 直旋混合射流钻头结构

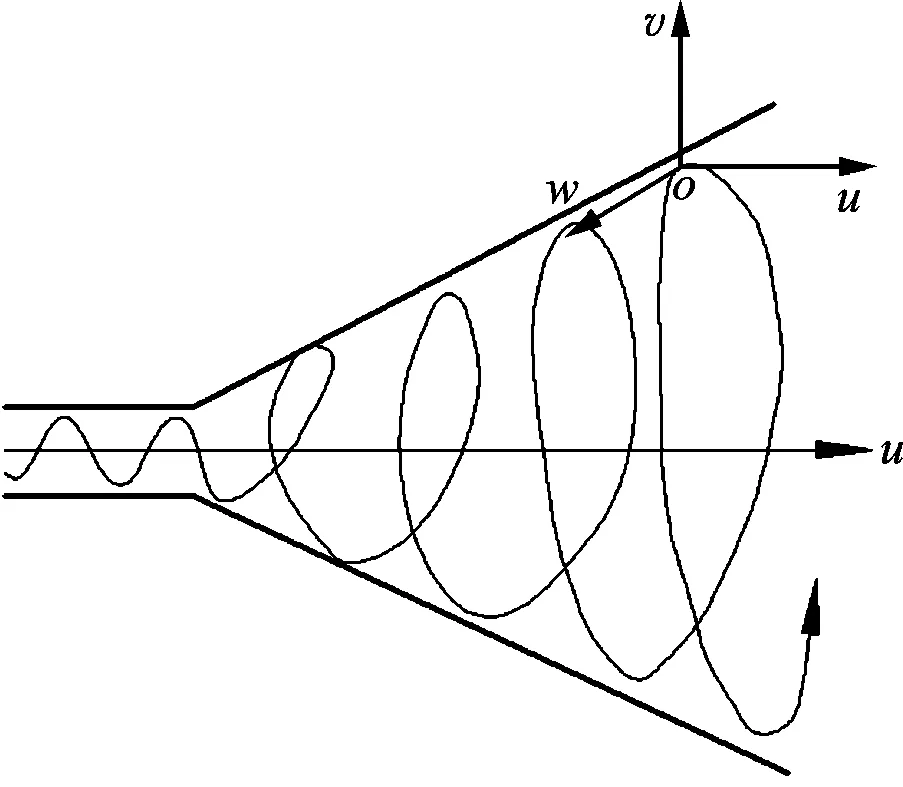
图2 射流速度分布

2 射流破岩对比实验

2.1 实验设备

本实验是在重庆大学煤矿灾害动力学与控制国家重点实验室完成。实验中:高压柴油泵(美国生产)的额定压力为138 MPa,额定流量为102 L/min;高压软管的工作压力为50 MPa;射流喷嘴(自行研发)如图3所示。由于本实验仅研究前喷嘴的射流破岩特性,故将钻头的后喷嘴去除。直旋混合射流喷嘴所用叶轮的中心孔直径dm为1.2 mm,旋转射流喷嘴的叶轮无中心孔,2种喷嘴的叶轮槽倾角θc均为45°。作为直射流喷嘴时将叶轮移除。3种射流喷嘴的出口直径df均为1.8 mm。冲蚀对象为致密砂岩,岩石的物理力学参数见表1。

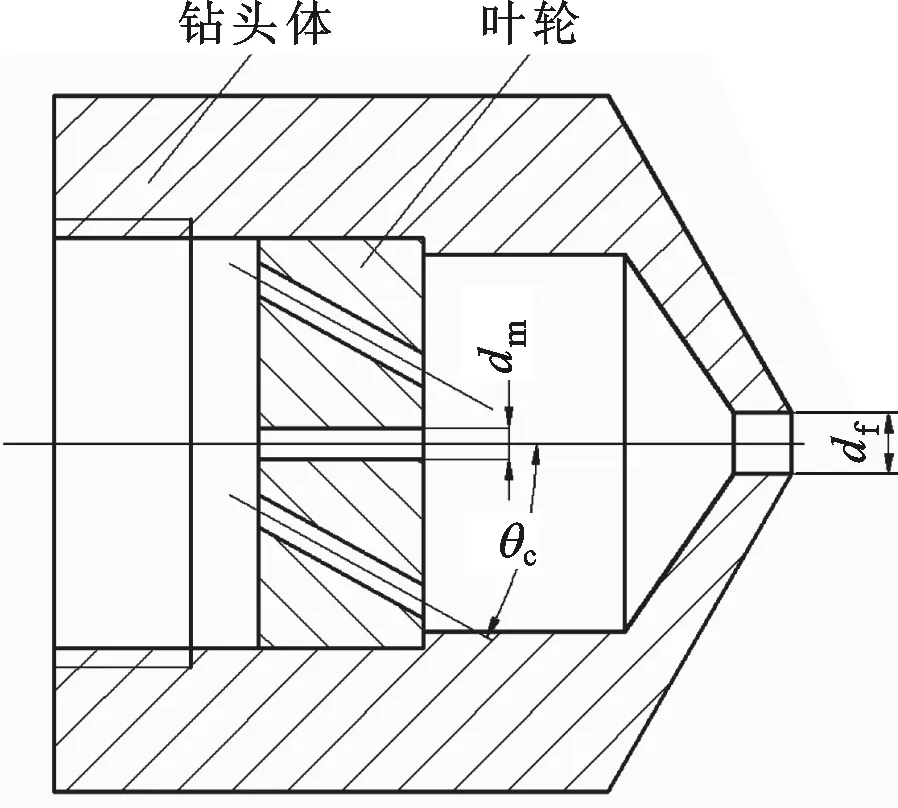
(a)结构尺寸

(b)实物图3 直旋混合射流喷嘴

岩石类型单轴抗压强度/MPa抗拉强度/MPa孔隙率/%砂岩62.974.549.53

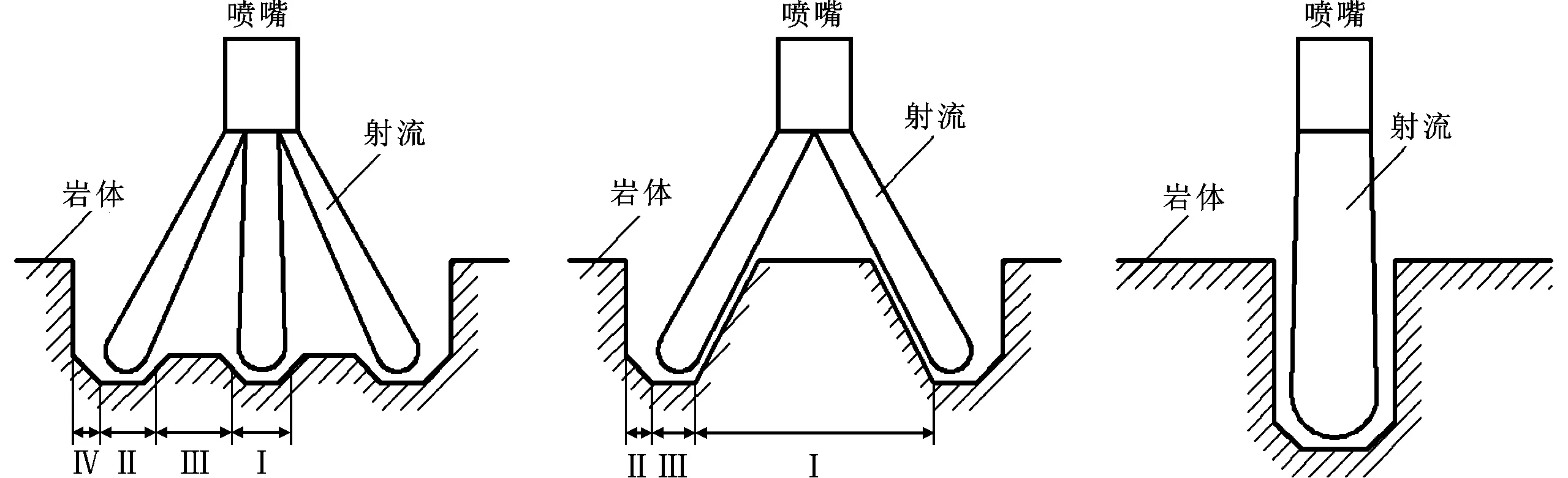
(a)直旋混合射流 (b)旋转射流 (c)直射流图6 冲孔形态示意图

2.2 实验方法及步骤

为保证实验数据的准确性,在喷嘴和岩石之间放置隔板,待实验的泵压稳定后撤掉隔板,同时开始计时,计时完成后插入隔板。为了消除测量带来的误差,对同一冲蚀孔、同一中心距下的不同位置的冲蚀深度进行测量,得到某一径向半径处的平均深度,并对同一冲蚀孔的不同周向位置处的直径进行测量,得到平均直径。为使数据具有对比性,每组实验采用相同的压力、靶距和冲蚀时间冲蚀同一类型的岩石,并对同一工况进行多组实验。泵压、靶距和冲蚀时间的选取应根据前期实验而定,本实验采用的泵压为34.5 MPa,靶距为10 mm,冲蚀时间为30 s。

射流破岩实验步骤包括:①安装射流喷嘴,检查流路的密封性;②调节靶距到设定值,在喷嘴和岩石之间放置隔板;③调节泵压到设定值,待压力稳定后撤掉隔板,同时开始计时;④冲蚀时间达到设定值之后,插入隔板;⑤卸压并关泵;⑥更换射流喷嘴,检查流路的密封性,重复步骤②～⑤,直至实验结束;⑦测量各冲孔的直径和不同径向半径处的深度。

2.3 实验结果及分析

3种射流的冲孔形状如图4所示。

图4 不同射流的冲孔形态

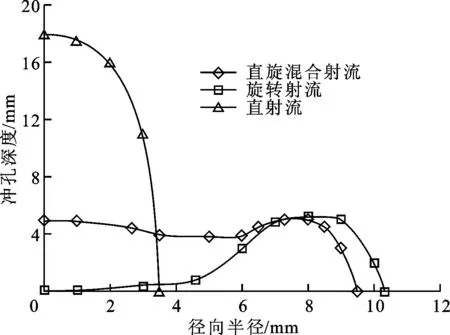
图5 不同射流的冲孔深度沿径向的分布规律

测量3种射流在不同径向半径处的深度,得到不同的射流冲蚀深度在径向上的分布规律,如图5所示,并绘制不同结构下冲孔的孔底形状,如图6所示。可以看出,3种射流的冲孔特性有很大差别,3种射流冲孔体积从大到小依次为:直射流—直旋混合射流—旋转射流,直射流获得较大破岩体积的同时孔径较小。理论上,由于叶轮的引入,采用直旋混合射流和旋转射流会增大流动损失,所以相比之下直射流能获得更大的破岩体积,但这并不表示直射流用于径向钻井技术是较优的。对于径向钻井技术来说,获得较大的破岩直径、满足钻头持续钻进是首要的。

从冲孔深度来看,直射流的冲孔深度最大,旋转射流的孔周较大且孔中心的深度接近于0,直旋混合射流的孔中心和孔周都较大;从冲孔直径来看,混合射流和旋转射流的冲孔直径比较大,直射流形成的孔直径远小于前2种射流;从冲孔孔底形状来看,旋转射流在中心存在凸台,直旋混合射流的孔底总体较为平整,仅存在微小的凹凸不平现象。直旋混合射流这种复杂的孔底形状说明了其在不同位置的流体质点对岩石的作用形式是不同的。

破岩特性与射流结构有关,下面通过3DPIV测试系统对3种射流的流场进行了研究。

3 流场测试对比实验

3.1 实验装置

1:水箱;2:过滤网;3:柱塞泵;4:溢流阀;5:流量计;6:压力传感器;7:喷嘴;8:激光;9:激光发生器;10:CCD相机;11:计算机图7 实验装置示意图

图7为实验装置示意图。实验中:BRW200/31.5型乳化泵的额定流量为200 L/min,工作压力为31.5 MPa;四维水射流测试平台是自行研发、设计的,用于承载3DPIV测试系统、控制喷嘴在任意方向的移动;直旋混合射流的喷嘴是自行研发、设计、加工的。3DPIV测试系统包括:激光器,输出能量为每一脉冲2×120 mJ,脉冲频率为15 Hz;CCD相机,分辨率为1 600 像素×1 200 像素,帧率为32帧/s,最短跨帧时间为200 ns;同步器,提供一对闪光灯和Q-开关信号,延时精度为15 ns;数据采集和处理软件,型号为INSIGHT3G-SEC,速度测试精度为±1.0%;射流喷嘴,其出口倒角为30°,便于侧后方相机拍摄。实验时,一台相机置于钻头的侧后方。

3.2 实验方法及步骤

实验开始之前,对2个相机的安置角度及位置反复进行调节、标定,再经测试误差分析得到最优相机的安置角度及位置。对不同工况进行了测试,即每种工况下的喷嘴出口流场连续拍摄200张图片。测试中速度场具有一定的偶然性,为保证数据的准确性,在分析射流轴向、径向和切向速度分布时取同一工况下10张清晰图片进行分析。

对于不同泵压下的射流流场特性,本作者已做过详细研究,结果表明,泵压的改变只会影响射流总体速度的大小,并不改变射流的速度分布规律。为了表征射流结构,将射流速度V进行相对化处理,即为任一流体质点速度与最大轴向速度umax的比值,包括相对轴向速度Vu、相对径向速度Vv和相对切向速度Vw,本文统一取umax为直旋混合射流的出口最大轴向速度。另外,相对径向半径为径向半径R与喷嘴直径df的比值。

流场测试实验步骤:①安装射流喷嘴;②将2个CCD相机与射流同侧,开启激光,调节激光头的位置,使激光片光源恰好位于射流轴心处;③打开Insight3G软件,设定硬件参数,运用三维标定靶盘标定CCD相机;④调节泵压到设定值,待压力稳定后,通过Insight3G软件调节实验参数,获取清晰图像;⑤卸压并关泵;⑥更换喷嘴,重复步骤④～⑤,直至测试结束;⑦利用Tecplot后处理软件对原始图像进行处理和计算。图8为流场测试中部分实验设备及实验过程。

图8 流场测试中部分设备及实验过程

3.3 实验结果及分析

图9为直旋混合射流的照片,图10为直旋混合射流的三维速度场。

(a)左相机 (b)右相机图9 直旋流混合射流照片

图10 直旋混合射流三维速度场

3.3.1 轴向速度场 3种射流轴向速度云图和喷距10 mm截面上速度沿径向的分布规律分别如图11和图12所示。可以看出:旋转射流最大轴向速度位于某一径向半径处,射流中心附近速度较低;直旋混合射流最大轴向速度位于射流轴线处,呈现中心最大且随着径向半径的增大逐渐减小;直射流的轴向速度和直旋混合射流相似,也呈现中心大的特性,但在径向的分布宽度上比直旋混合射流和旋转射流小得多,即直射流的速度最为集中,这与破岩实验结果相吻合。由于旋转射流中心低速区的存在,使得冲孔的中心位置出现凸台,而直旋混合射流又因中心直射流的存在,使得轴心处的速度为最大,进而钻孔的中心不会出现凸台;直射流速度集中于射流轴心处,其对岩石在径向的打击范围较小,所以钻孔深度深,但直径较小。

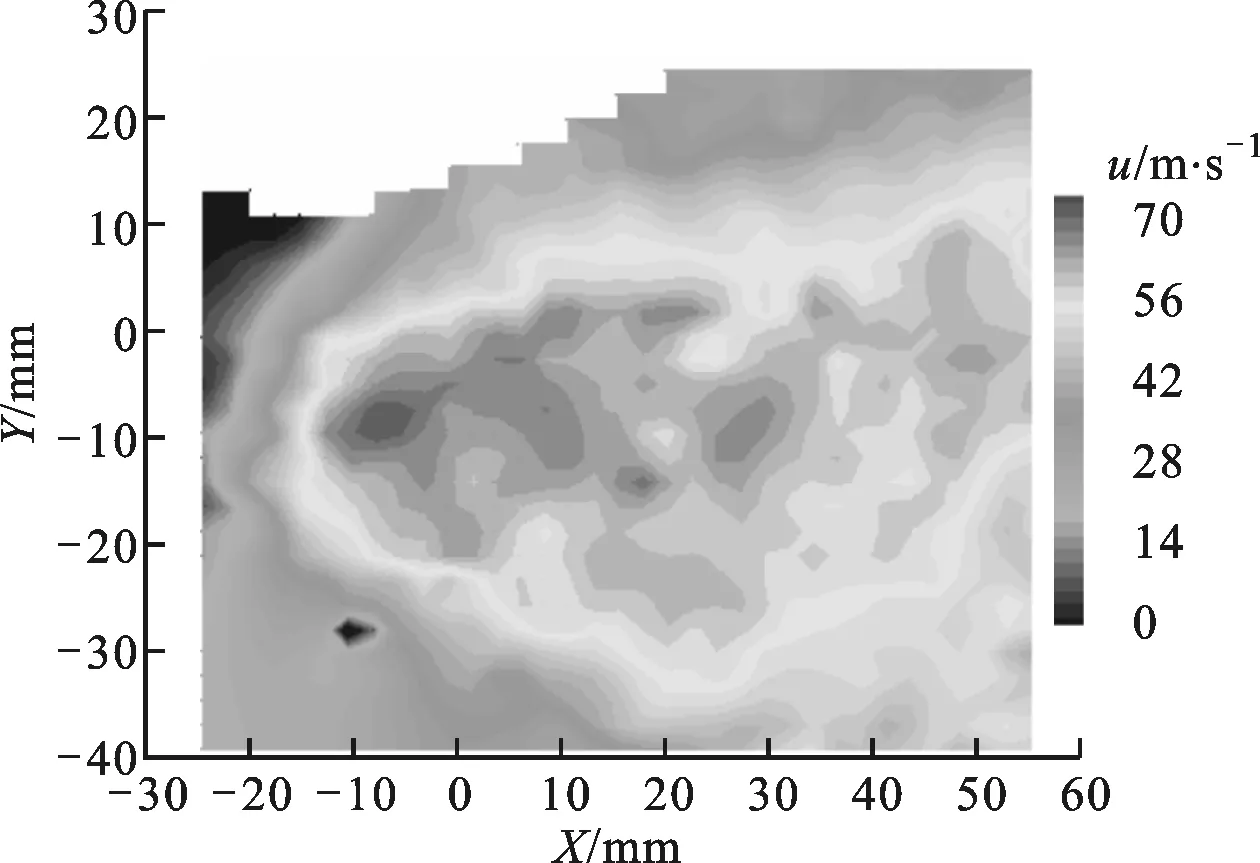
(a)直旋混合射流

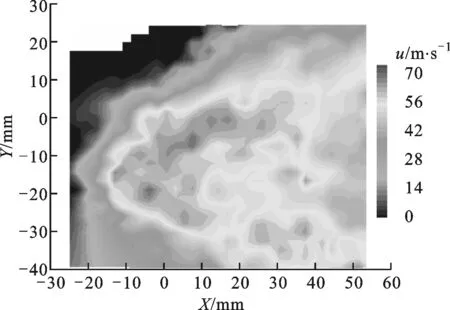
(b)旋转射流

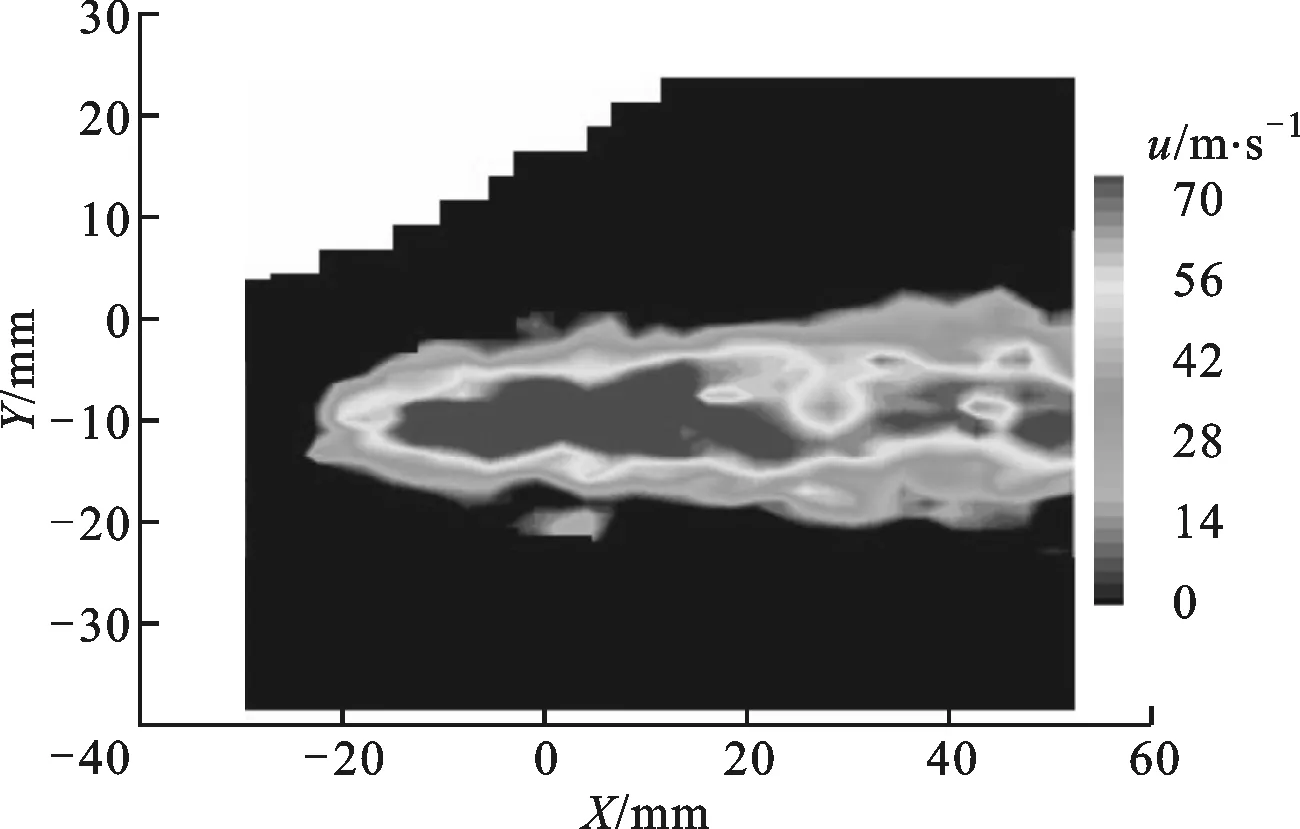
(c)直射流图11 3种射流轴向速度场

图12 3种射流轴向速度沿径向的分布规律

3.3.2 径向速度场 根据已有射流理论,直射流的径向速度很小,可以忽略不计,此处不作分析。直旋混合射流和旋转射流的径向速度云图和喷距10 mm截面上速度沿径向的分布规律分别如图13和图14所示。可以看出:直旋混合射流和旋转射流的径向速度最大值在一定的径向半径处,射流轴线附近的径向速度约为0,射流在离开喷嘴后,喷距越大,径向速度在径向的分布范围越大,径向速度的作用是使射流产生扩散,扩散大小决定了射流在径向的分布范围;旋转射流的径向速度最大值略大于直旋混合射流,最大值位于R/df=4.4处,而直旋混合射流最大径向速度位于R/df=5.7处,这说明在同一叶轮槽倾角下,旋转射流的扩散能力略大于直旋混合射流。

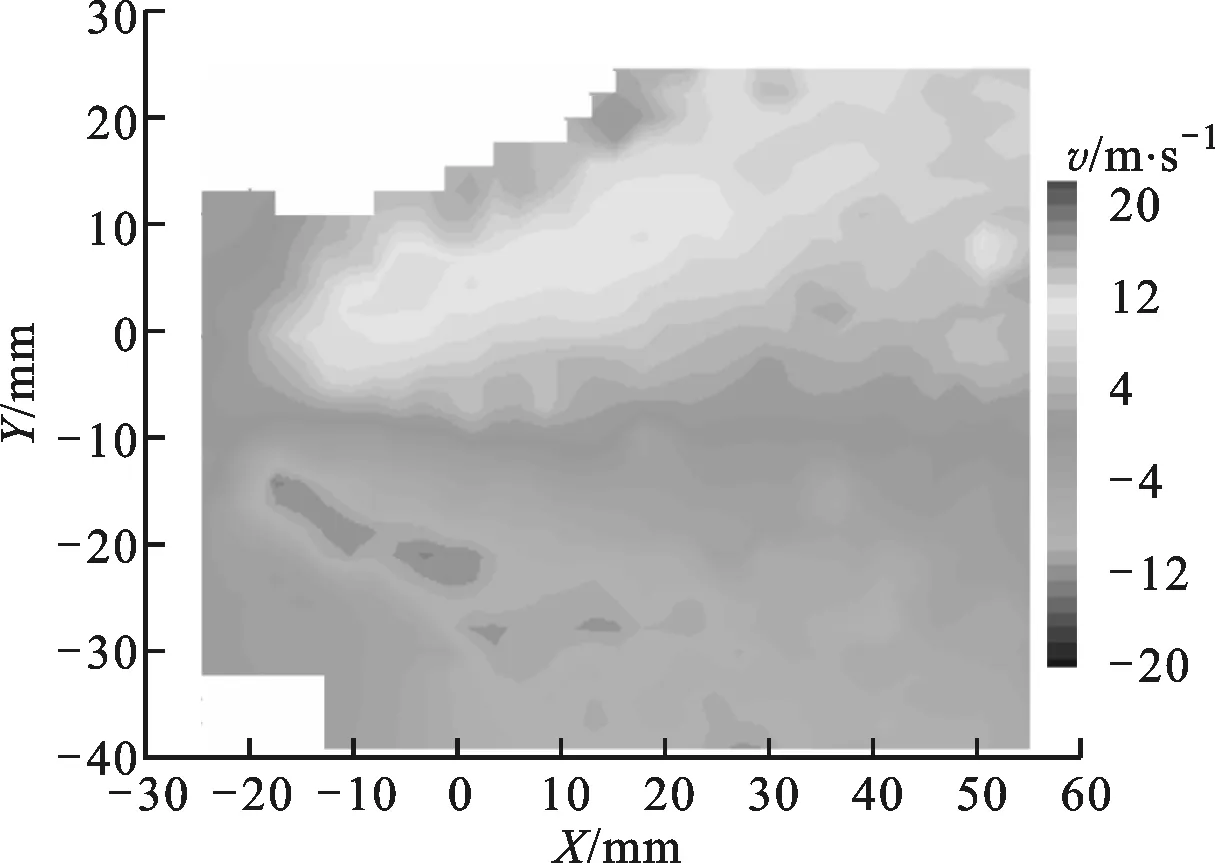
(a)直旋混合射流

(b)旋转射流图13 2种射流径向速度场

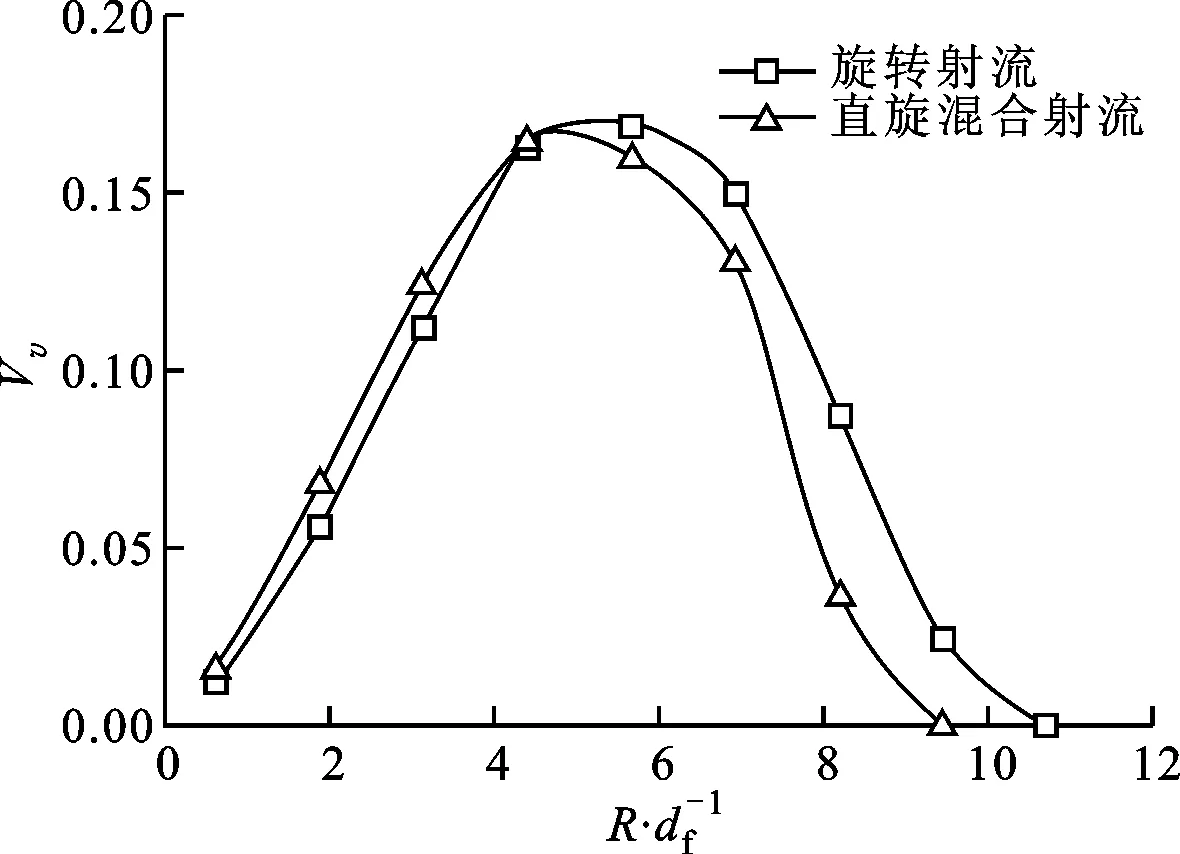
图14 2种射流径向速度沿径向的分布规律

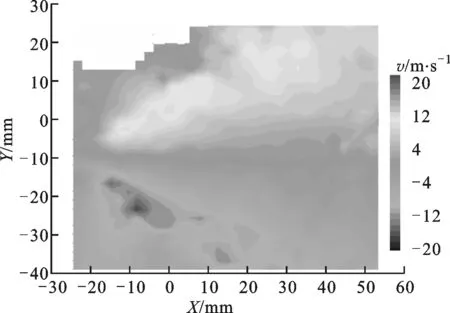
3.3.3 切向速度场 根据已有的理论,直射流不存在切向速度,故此处不作分析。图15为旋转射流和直旋混合射流切向速度云图,切向速度垂直于平面,以垂直平面向外的速度方向为正值,垂直平面向内的速度方向为负值。图16为喷距10 mm截面上速度沿径向的分布规律。可以看出,射流切向速度分布规律和径向速度类似,但同一质点的切向速度远大于径向速度,喷距10 mm截面上旋转射流的最大切向速度略大于混合射流。

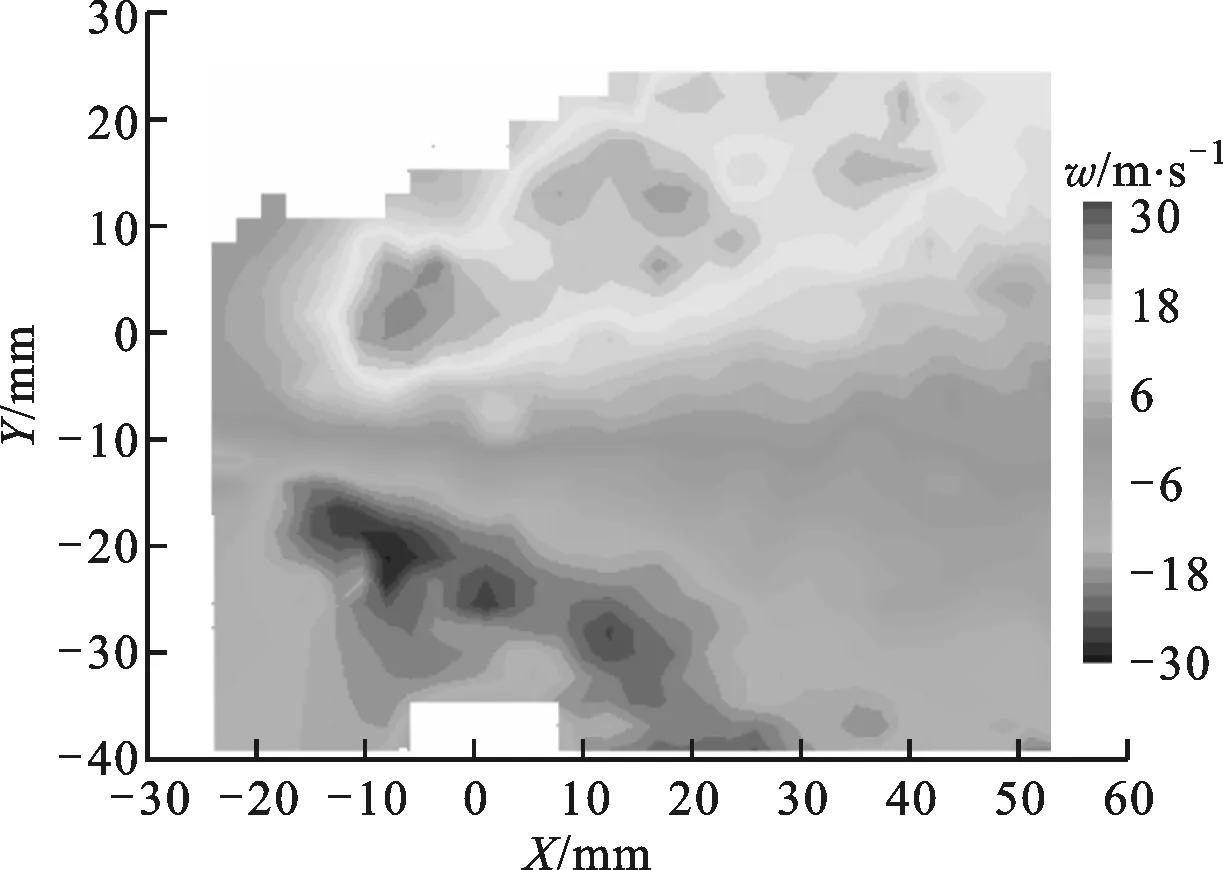
(a)直旋混合射流

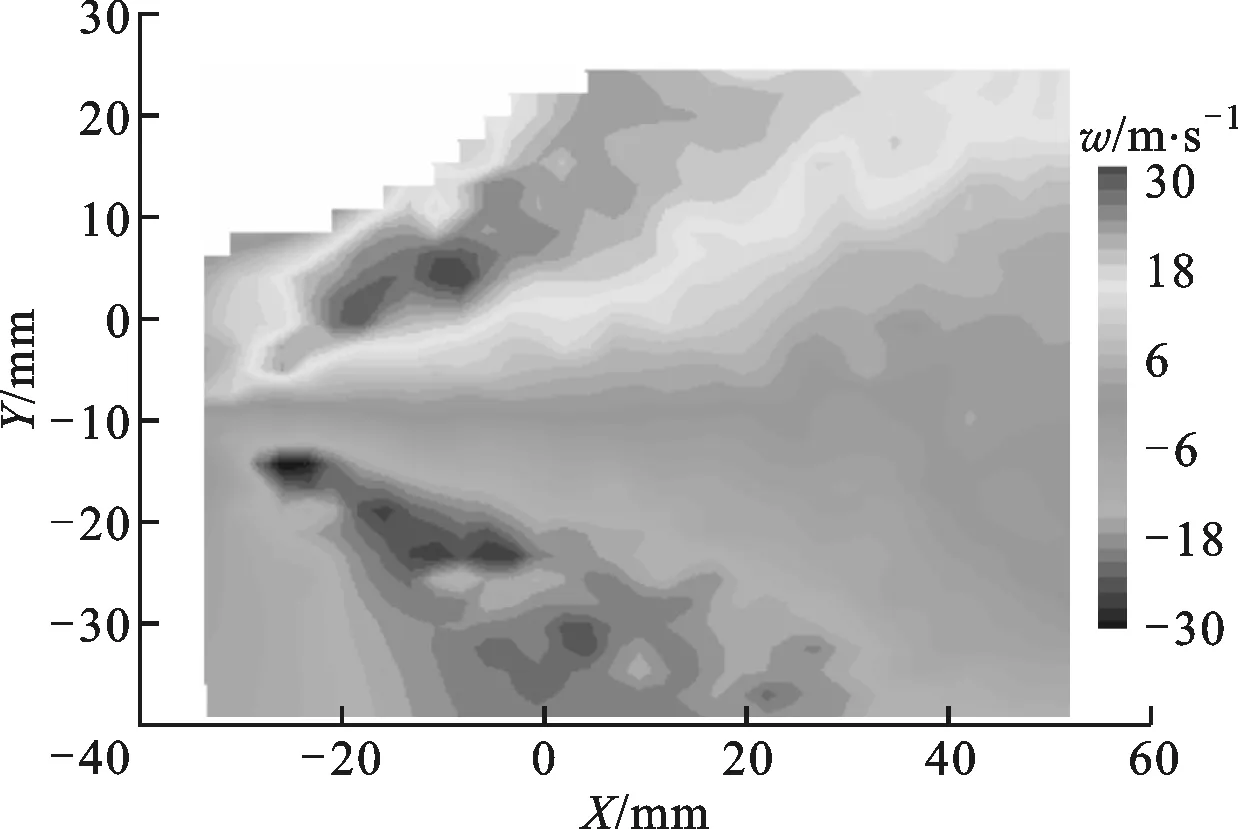
(b)旋转射流图15 2种射流切向速度场

图16 2种射流切向速度沿径向的分布规律

以上3种射流的轴向、径向和切向速度分析结果与破岩实验结果相吻合。由于旋转射流轴线附近速度较低,使得该处射流的正向冲击能力较弱,冲孔的中心位置出现凸台;由于直旋混合射流中心存在直射流,使得射流轴线附近的速度较大,其消除了中心低速区,进而钻孔的中心不会出现凸台。旋转射流的径向和切向速度在径向上的分布范围都略大于直旋混合射流,这决定了旋转射流的钻孔直径略大于直旋混合射流;直射流以轴向速度为主,具有很小的径向速度,不存在切向速度,射流的能量密集区集中于射流轴心附近,其对岩石径向打击范围较小。

4 直旋混合射流破岩特性及机理分析

4.1 流场与破岩特性的关系

图17为靶距在10、15、20 mm下岩石的冲孔形态。可以看出,不同靶距下的孔底形态均呈现中心和孔周较大的特点。图18为喷距在10、15、20 mm处的射流速度分布。可以看出,冲孔形态与射流特性有密不可分的关系。对于不同靶距下的冲孔中心,其对应位置射流的合速度U和轴向速度都是最大的;对于不同靶距下冲孔的孔周,其对应位置射流合速度和轴向速度不为最大,但径向速度和切向速度都是最大的。这说明射流破岩能力不仅与射流能量有关,还与射流的方向有很大关系。

图17 不同靶距下钻孔形态

以靶距10 mm下岩石的冲孔形状和相应喷距下的射流速度沿径向的分布为例进行了分析。根据3DPIV的流场测试结果可以看出,直旋混合射流的轴向速度明显大于径向速度和切向速度,3个方向的速度在径向上的分布半径大致相同。分析该靶距下的冲孔形状,在射流的径向半径0处,即射流中心,射流形态主要为直射流,根据射流理论和3DPIV的分析,该射流仅具有轴向速度,径向和切向速度接近于0,但中心直射流的轴向速度和合速度都为最大,进而射流的能量最大,这样便消除了单纯旋转射流的中心低速区且冲孔深度较大的问题。随着径向半径的增大,射流的径向和切向速度逐渐增大,轴向速度逐渐减小,与轴向速度相比径向和切向速度仍然较小,所以该处的轴向速度起主导作用,但合速度逐渐下降,相应的射流能量下降,对应位置的破岩深度减小;随着径向半径的继续增大,在径向半径8.0 mm处径向和切向速度都达到最大,轴向速度和合速度继续下降,所以该处的射流能量减小,但根据冲孔形状来看,该处的破岩深度最深,可以判断破岩能力除了与射流能量有关,还与射流的作用方式有关;在长向半径8.5 mm处径向和切向速度仍较大,轴向速度下降较快,使得合速度下降较快,进而冲孔的深度减小,当径向半径进一步增大使得合速度过小时,射流能量不足以破碎岩石。

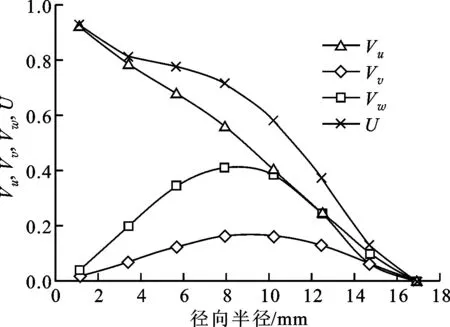
(a)喷距10 mm

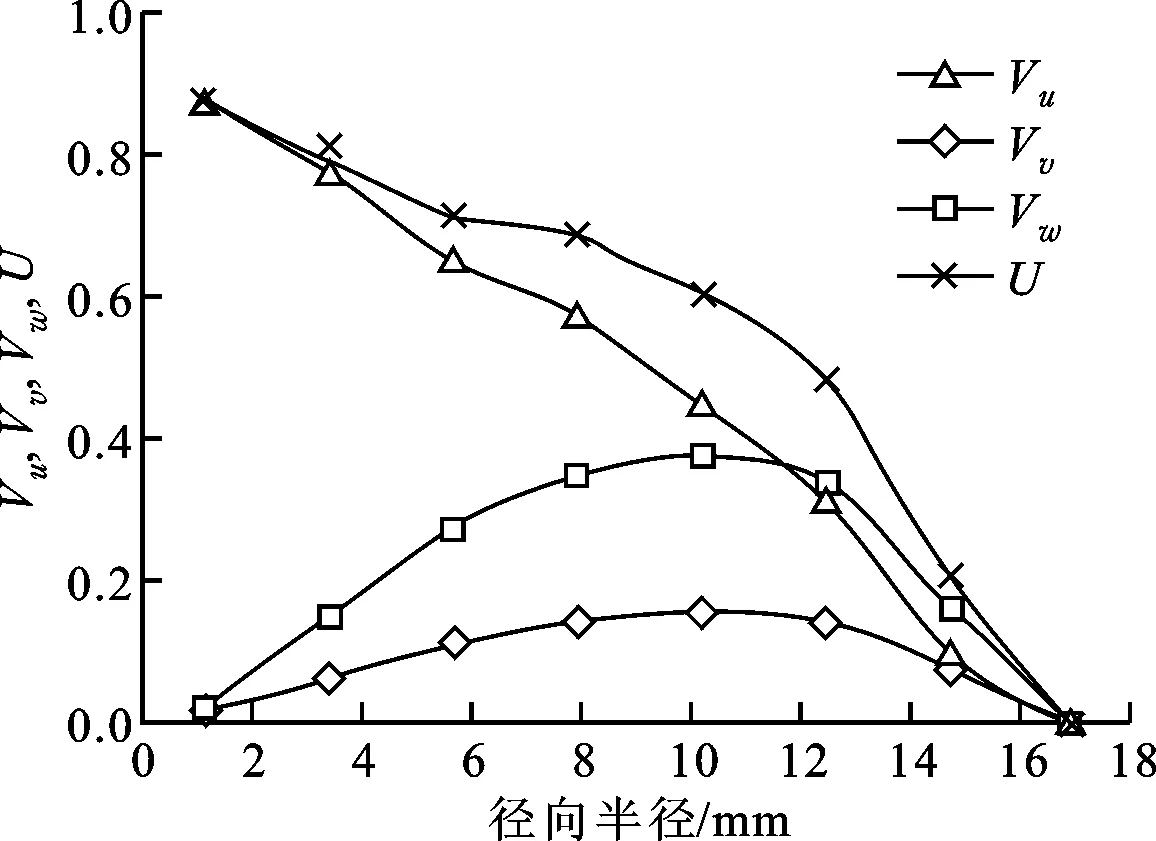
(b)喷距15 mm

(c)喷距20 mm图18 不同喷距下射流速度分布规律

图17中A、B为破岩最深的位置,分别为4.9、5.1 mm,A位于钻孔的中心,B位于径向半径8 mm处,从合速度来看,A的速度要大于B,但B的破岩深度略大于A。A对应的射流具有最大的轴向速度,径向和切向速度接近于0,而B的径向和切向速度为最大,对岩石不仅具有正向冲击作用,还施加了径向张力和周向剪力。岩石的抗拉和抗剪强度相比抗压强度低得多[13],岩石内容易产生微裂隙,在射流的准静态压力作用下微孔隙、微裂纹会产生二次扩展,使得最终破岩成功。此外,由于切向和径向速度的存在,流体质点的速度方向不垂直于岩石表面,所以流体不会沿原路返回,而是沿射流的外围返回[14],这样不会产生水垫效应,进而不会阻碍后续射流对岩石的冲击作用。

4.2 直旋混合射流破岩机理分析

本文将直旋混合射流划分为4个区域:直射流区、强旋射流区、弱旋射流区和外围射流区,如图19所示。

图19 直旋混合射流破岩示意图

根据众多学者的研究和论证,水射流作用下岩石的主要破坏形式可分为3种,即冲击动载荷和水锤压力等作用下的初始破碎,冲击作用下周边岩石的微裂隙损伤积累,宏观裂隙扩展下的阶跃式体积破碎[15-19]。

对于直旋混合射流,破岩在时序上也可以分为以下3个阶段。

(1)射流冲击岩石形成初始破碎坑。直射流区具有较高的射流能量,且能量较为集中,射流与岩石垂直作用为正向的射流冲击。强旋射流区的射流与岩石之间有一定的冲击角度,具有较大的径向和切向速度,对岩石不仅具有正向冲击作用,还施加了径向张力和周向剪力。这2个区域对应的冲孔最深,但强旋射流区的破岩效率更高。弱旋射流区轴向速度小于直射流区,径向和切向速度又小于强旋射流区,所以该区的射流冲蚀能力相对较弱。外围射流区射流能量和旋流强度都较小,破碎能力较弱,在该区形成了一个沿径向深度不均的初始破碎坑。

(2)在破碎坑周围产生诸多微孔隙、微裂纹。旋转射流存在拉伸和剪切效应,比直射流更容易导致岩石产生裂隙和裂纹,弱旋射流区介于强旋射流区和直射流区之间,在弱旋射流区直射流和旋转射流会使得岩石周围产生微孔隙、微裂纹。

(3)射流在准静态压力作用下引起宏观体积性破碎。直旋混合射流各个区域的流体通过渗透、楔入使得岩石内部流体与外部高压射流流体相互连通而形成压力体,射流压力能够传递到岩石内部的微裂纹和微孔隙,转化为流体的准静态压力,而流体进入岩石固有的空隙或新形成的裂隙、裂纹之中,对岩石产生水楔效应,使裂纹在张力作用下形成二次扩展,扩展的微裂纹不断汇聚、连通,最终形成宏观的岩石破碎。直射流和旋转射流对弱旋射流区的岩石周围产生损伤,由此降低了岩石的强度,使得在较小的射流能量和较弱的旋度亦能有效破碎岩石。

经过以上3个阶段后,破岩区域产生新的自由面,重复以上的破岩过程,射流与岩石间的距离逐渐增大,作用于岩石表面的射流能量也逐渐衰减,钻孔形态逐渐趋于稳定。

综上所述,直旋混合射流的破岩机理为:直射流区具有最大的射流能量,射流与岩石表面垂直,破岩主要靠射流的正向冲击作用;强旋射流区具有最大的径向、切向速度和旋流强度,对岩石产生拉伸和剪切破坏,加上正向的冲击作用,且不存在水垫效应,从而保证了该区域具有很高的破岩效率;弱旋射流区介于直射流区和强旋射流区之间,该区域对应的岩石周围受到直射流和强旋射流的联合作用,由此降低了该区域岩石的强度,从而使弱旋射流亦能有效破碎岩石;外围射流区的破岩特性为射流携带岩屑对孔壁起磨削作用,使钻孔直径进一步扩大。

所以,直旋混合射流有效解决了直射流破岩孔径小、旋转射流破岩容易出现孔底中心凸台的问题。直旋混合射流在4个分区的大小及形状等特性受到喷嘴结构的影响,在喷嘴结构确定的条件下,水力能量越高,钻孔深度和直径越大,这有利于提高钻进速度。

5 结 论

本文通过冲蚀实验和3DPIV测试系统揭示了冲孔形态与射流流场特性的关系,得到了直旋混合射流的破岩机理,具体的结论如下。

(1)直旋混合射流结合了直射流和旋转射流的优势,能够钻出直径较大和深度较深的孔,孔底形状稍有凹凸不平现象,但整体较为平整。

(2)直旋混合射流流场沿径向分布宽度较大,射流中心不存在低速区,其与直射流、旋转射流相比,具有更优的钻孔能力,符合水力喷射径向钻井技术对钻孔的要求。

(3)直旋混合射流在4个分区的破岩特性各不相同。直射流区具有最大的射流轴向速度及合速度;强旋射流区具有最大的径向速度和切向速度;弱旋射流区破岩特性在于受到直射流和强旋射流的共同作用,岩石强度降低;外围射流区的破岩特性具有磨料射流效应,可使钻孔直径进一步扩大。

[1] 宋岩, 张新民, 柳少波. 中国煤层气基础研究和勘探开发技术新进展 [J]. 天然气工业, 2005, 25(1): 1-7, 204. SONG Yan, ZHANG Xinmin, LIU Shaobo. Progress in the basic studies and exploration & development techniques of coalbed methane in China [J]. Natural Gas Industry, 2005, 25(1): 1-7, 204.

[2] 董大忠, 邹才能, 李建忠, 等. 页岩气资源潜力与勘探开发前景 [J]. 地质通报, 2011, 30(2/3): 324-336. DONG Dazhong, ZOU Caineng, LI Jianzhong, et al. Resource potential, exploration and development prospect of shale gas in the whole world [J]. Geological Bulletin of China, 2011, 30(2/3): 324-336.

[3] OURSEGOV S, PETROV N. Design and initial performance of pilot cyclic steam stimulations of vertical wells with radial horizontal bores in low-permeable heavy oil carbonates, SPE 115125 [R]. Richardson, Texas, USA: SPE, 2008.

[4] SALEM P D, KAMEL A M. Radial drilling technique for improving well productivity in petrobel-Egypt [C]∥North Africa Technical Conference and Exhibition. Richardson, Texas, USA: SPE, 2013: 164773

[5] DICKINSON W, ANDERSON R R, DICKINSON R W. The ultrashort-radius radial system [J]. SPE Drilling Engineering, 1989, 4(3): 247-254.

[6] BRUNI M A, BIASOTTI J H, SALOMONE G D. Radial drilling in Argentina [C]∥Latin American & Caribbean Petroleum Engineering Conference. Richardson, Texas, USA: SPE, 2007: 107382.

[7] 沈忠厚. 水射流理论与技术 [M]. 山东东营: 石油大学出版社, 1998.

[8] 周定伟, 马重芳, 任玉涛. 圆形浸没射流冲击下有关压力梯度的理论分析 [J]. 西安交通大学学报, 1999, 33(7): 56-58, 85. ZHOU Dingwei, MA Chongfang, REN Yutao. Theoretical analysis of pressure gradient under impinging submerged round jets [J]. Journal of Xi’an Jiaotong University, 1999, 33(7): 56-58, 85.

[9] 李根生, 宋剑, 牛继磊, 等. 高压旋转双射流钻孔方法及其高压旋转双射流喷嘴: 中国, CN1959058 [P]. 2007-05-09.

[10]BUCKMAN W G, DOTSON T L, MCDANIELS M D, et al. Nozzle for jet drilling and associated method: USA, 6668948 [P]. 2003-12-30.

[11]MA D J, LI G S, ZHANG X, et al. Experimental study on rock breaking by a combined round straight jet with a swirling jet nozzle [J]. Atomization & Sprays, 2011, 21(8): 645-653.

[12]LIAO H L, WU D S, WANG L, et al. Comparisons of spraying structure and rock breakage characteristics of round straight, swirling, and straight-swirling integrated jets [J]. Atomization & Sprays, 2013, 23(4): 363-377.

[13]步玉环, 王瑞和, 周卫东, 等. 旋转射流破岩成孔规律研究 [J]. 岩石力学与工程学报, 2003, 22(4): 664-668. BU Yuhuan, WANG Ruihe, ZHOU Weidong, et al. Study on rock drilling by swirling jet [J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(4): 664-668.

[14]王瑞和, 周卫东, 沈忠厚, 等. 旋转射流破岩钻孔机理研究 [J]. 中国安全科学学报, 1999, 9(z1): 1-5. WANG Ruihe, ZHOU Weidong, SHEN Zhonghou, et al. Study on mechanism of rock-breaking by swirling water jet [J]. China Safety Science Journal, 1999, 9(z1): 1-5.

[15]BIENIAWSKI Z T. Mechanism of brittle fracture of rock: part I Theory of the fracture process [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1967, 4(4): 395-406.

[16]FORMAN S E, SECOR G A. The mechanics of rock failure due to water jet impingement [J]. Society of Petroleum Engineers Journal, 1974, 14(1): 10-18.

[17]王瑞和, 倪红坚. 高压水射流破岩机理研究 [J]. 石油大学学报: 自然科学版, 2002, 26(4): 118-122. WANG Ruihe, NI Hongjian. Research of rock fragmentation mechanism with high-pressure water jet [J]. Journal of The University of Petroleum: Edition of Natural Sciences, 2002, 26(4): 118-122.

[18]倪红坚, 王瑞和, 张延庆. 高压水射流作用下岩石破碎机理及过程的数值模拟研究 [J]. 应用数学和力学, 2005, 26(12): 1445-1452. NI Hongjian, WANG Ruihe, ZHANG Yanqing. Numerical simulation study on rock breaking mechanism and process under high pressure water jet [J]. Applied Mathematics and Mechanics, 2005, 26(12): 1445-1452.

[19]倪红坚, 王瑞和. 脉冲水射流破岩的数值模拟研究 [J]. 石油钻探技术, 2001, 29(5): 12-14. NI Hongjian, WANG Ruihe. Numerical simulation study on pulse water jet crashing rock [J]. Petroleum Drilling Techniques, 2001, 29(5): 12-14.

(编辑 苗凌)

Characteristics and Mechanism of Rock Breaking for New Type Straight-Swirling Integrated Jet

DU Peng1,2,LU Yiyu1,2,TANG Jiren1,2,ZHOU Zhe1,2,ZHANG Wenfeng1,2

(1. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400030, China;2. National & Local Joint Engineering Laboratory of Gas Drainage in Complex Coal Seam,Chongqing University, Chongqing 400030, China)

To reveal the rock breaking mechanism of straight-swirling integrated jet, the erosion experiments of straight jet, swirling jet and straight-swirling integrated jet were carried out, and the velocity fields of the three jets were obtained by 3DPIV. The damage characteristics of straight-swirling integrated jet were revealed via comparative analyses for distribution laws of hole depth and jet velocity along radial direction at the same target distance. The results show that the straight-swirling integrated jet eliminates the low velocity area and the hole center boss of swirling jet, and both the jet distribution width and hole diameter are bigger than those of straight jet. The jet structure can be divided into straight jet area, high swirl strength jet area, low swirl strength jet area and periphery jet area; the jet energy of straight jet area decides the capacity of rock breaking; high swirl strength jet area has high radial and tangential velocity, thus long depth hole near that by straight jet can be drilled by radial tension and circumferential shearing force under the condition of resultant velocity lower than straight jet; rocks in low swirl strength jet area are damaged by both straight and swirling jets, which decrease the rock strength, and the broken rocks can be transported effectively in this lower velocity area, where rock breaking of periphery jet area results from the wearing of returning jet with rock debris.

radial drilling; straight-swirling integrated jet; rock breaking mechanism; flow field

10.7652/xjtuxb201603013

2015-10-13。 作者简介:杜鹏(1987—),男,博士生;卢义玉(通信作者),男,教授,博士生导师。 基金项目:国家重点基础研究发展计划资助项目(2014CB239206);国家自然科学基金资助项目(51404045,51374258);长江学者和创新团队发展计划资助项目(IRT13043);中央高校基本科研业务费专项资金资助项目(CDJZR12248801)。

时间:2015-12-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20151210.1133.012.html

TE21

:A

:0253-987X(2016)03-0081-09