基于遗传算法的运行模式分布模型及排放测算
2016-12-23胥耀方宋国华重庆交通大学交通运输学院重庆400074美国德克萨斯南方大学美国休斯顿77004北京交通大学北京100044
胥耀方,于 雷,宋国华(1.重庆交通大学交通运输学院,重庆 400074;2.美国德克萨斯南方大学,美国 休斯顿 77004;.北京交通大学,北京 100044)
基于遗传算法的运行模式分布模型及排放测算
胥耀方1*,于 雷2,3,宋国华3(1.重庆交通大学交通运输学院,重庆 400074;2.美国德克萨斯南方大学,美国 休斯顿 77004;3.北京交通大学,北京 100044)
针对交通系统易于收集到的平均速度,以及排放模型计算所需的运行模式分布参数,建立基于平均速度的运行模式分布模型,并采用遗传算法对模型进行优化.对比所建立模型、MOVES模型中的行驶周期所获取数据与真实数据之间的排放结果差异,发现本模型有82.5%的区间平均排放率预测误差低于MOVES,本模型的最大误差为50.0%,而MOVES模型为304.2%.使用本模型评价了北京市限行前后污染物排放情况,发现限行后二环路高峰小时HC、CO、NOx总体排放依次减少了9.58%、11.41%、0.49%.与真实值相比,预测值R2方高于0.700,预测误差大幅度低于MOVES模型预测误差,并实现对交通策略下路网排放的动态评价应用.
运行模式分布;排放测算;平均速度;遗传算法
目前,国际上主要采用的 MOVES[1](Motor Vehicle Emission Simulator)、 CMEM[2](Comprehensive Modal Emission Model)、VT-Micro[3](Virginia Tech Microscopic energy and emission model、IVE[4](International Vehicle Emission Model)等机动车尾气排放模型,均引入了运行模式参数进行排放测算.相比于过去基于平均速度的路网排放测算方法[5],基于运行模式的排放测算方法,更适用于细致地描述不同交通状态下的排放变化情况.尤其是运行模式中的VSP(Vehicle Specific Power)参数,不仅可以从物理角度清晰地解释机动车排放,并且还与排放速率有着更好的拟合关系,因此在国内外取得广泛应用:陈长虹等[6]、潘汉生等[7]、王岐东等[8]、曲亮等[9]发现 VSP与车辆污染物排放存在较好的相关性;Zhang等[10]利用VSP变量建模方法对不同信号配时进行排放分析;杨方[11]、Liu等[12]建立了包含VSP为变量的车辆排放模型.
目前基于VSP的排放研究中,测试车辆往往不超过10辆.这是因为获取VSP参数时,需要逐秒的速度、加速度、坡度等信息,而基于目前通信水平和硬件成本,难于在路网范围内大规模推广收集.陈琨等[13]曾用 VISSIM对北京市一个 7个节点的路网进行了15min的交通排放模拟,整个过程耗时 5h40min.不过,依靠目前的数据采集设备,如浮动车系统或交通规划类软件,却可以提供相当可靠的平均速度.因此,美国环保署发布的MOVES模型,在路网等宏观层面采用平均速度对应行驶周期的方式计算车辆运行模式,进而获取排放数据.但行驶周期的样本量非常有限,导致其计算的VSP分布很不稳定,无法动态刻画路网在不同交通状态下的排放情况.
因此,很多学者开始分析平均速度与VSP之间的关系.Lents等[14]发现奈落比,圣利亚哥,圣保罗三个城市有着相似的VSP分布.Frey等[15]发现13组平均速度在30~40km/h区间的数据VSP分布类似.宋国华等[16]发现不同平均速度下,VSP分布呈现正态分布,且均值随平均速度的增大而增大.这些研究揭示了平均速度之间与VSP分布的强相关性,但尚未建立平均速度和VSP分布组合区间的直接数学关系,无法直接建模量化路网排放.
因此,本文以排放模型所需的交通参数为目标,研究基于平均速度的机动车运行模式分布模型,从而实现交通网络的排放测算.由于目前中国尚无官方发布的标准化机动车排放模型,本文参考美国环保署发布的 MOVES机动车排放模型所需参数,以VSP和瞬时速度的组合定义运行模式,从而建立不同平均速度下,机动车运行模式分布模型.
1 方法
1.1 数据采集
1.1.1 数据采集方案 建模选择北京市46辆轻型车进行GPS数据收集,其信息包括速度、经纬度等,实验路线如图1所示.实验时间包含周末与工作日,时段包含平峰与高峰.实验共收集到快速路数据608744条.选择2辆车在15km的快速路上运行的数据进行模型排放测算,实验路线如图2所示,共收集数据13462条.
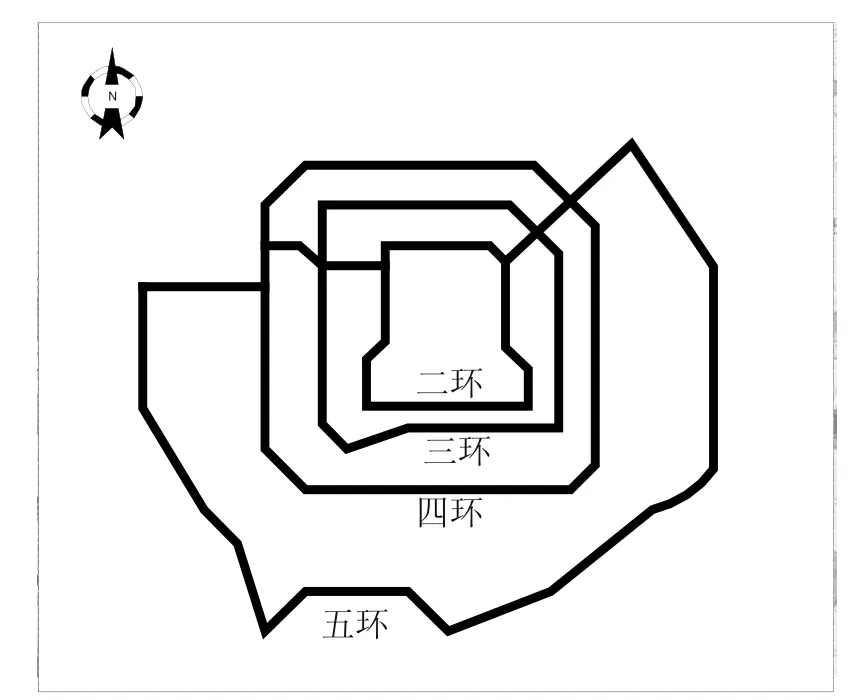
图1 建模数据收集路线Fig.1 The testing route for model development

图2 排放测算数据收集路线Fig.2 The testing route for the evaluation of emission
1.1.2 数据处理方法 (1)考虑北京市的平原地形,假设坡度值为 0,则利用公式(1)[17]计算车辆VSP值.

式中:v为机动车速度,m/s; a为机动车加速度, m/s.
(2)与排放模型MOVES对应,划分运行模式:首先将瞬时速度分为 0~1.5km/h;1.5~40km/h;40~80km/h和80km/h以上区间;再按1kW/t为间隔进行VSP区间划分,并与各瞬时速度区间组合.
(3)本文以1min为时间步长计算平均速度,并按2km/h进行分段,将收集到的逐秒数据分隔为多个片断,并将相同平均速度下的片断进行叠加.
(4)计算各平均速度区间中,不同VSP与瞬时速度组合(运行模式)区间的样本量占该平均速度总样本量的比例.
1.2 数据分类
经1.1处理后的数据如图3所示,图中横坐标为VSP区间和瞬时速度区间共同组成的运行模式组合区间,其中VSP区间编号表示其对应的等值VSP,而瞬时速度1区间、2区间、3区间、4区间分别对应瞬时速度为0~1.5km/h;1.5~ 40km/ h;40~80km/h和80km/h以上区间.由图可见,瞬时速度0~1.5km/h区间的值集中于VSP∈[-0.5,0.5] kw/t 区间,呈单一分布模式,与其他区间的分布规律不同,故在后文中单独讨论;而1.5~40km/h、40~80km/h区间的分布形态较为类似,即VSP分布分别都呈“钟摆”态,即以最高出现频率为轴,两侧区间分布频率对称性下降的形态,故将这两个区间合并讨论,其分析建模及改进过程见 1.3与1.4;80km/h以上区间的样本量过少,以至不足以再划分平均速度区间,故将其数据合并后再建模,此区间在2.4中单独讨论.
1.3 高斯拟合以及存在问题
在瞬时速度 1.5~40km/h、40~80km/h区间,各平均速度下的VSP分布都呈“钟摆”态,如图4,即以最高出现频率为轴,两侧区间分布率对称性下降的形态.且随着平均速度的上升,钟摆宽度加大,即平均速度越高,宽度越宽,同时对称轴逐渐右移.运行模式分布的“钟摆”形态与高斯函数的图像特征非常吻合,因此,本文引入高斯函数,验证其对VSP分布图像的拟合效果.
高斯函数的函数形式如下:

式中:a、b、c为高斯参数,其中,a为函数的峰值高度;b为函数的对称轴;c控制函数图像的宽度.
虽然高斯函数可以对瞬时速度1.5~40km/h、40~80km/h区间运行模式分布拟合,但却普遍存在离对称轴较远处估计值偏低的现象,如图4所示.提出以下解决方法:以对称轴两侧一定距离进行分段,令包含对称轴的部分为中心区域,不包含对称轴的部分为边缘区域,如图5所示.对于不同区域,则可按高斯拟合与实际情况的差异,对各高斯参数分别进行不同比例的缩放改进.因此,改变峰值高度、钟摆宽度或是对称轴位置,从而使高斯曲线与实际运行模式更加逼近,提高边缘区域的预测值以至更接近真实值.具体做法为:以原有高斯函数中参数b所确定的对称轴为中心,向其两侧进行延伸,并分别对不同区域影响高斯函数峰值、对称轴、和宽度的参数a、b、c进行缩放.缩放前,为降低模型复杂度,将相同瞬时速度的区间归为同一类,即分为1.5~40km/h与40~80km/h两类区间.在每类区间中,对称轴向外延伸的距离长度相同,高斯参数的缩放比例也相同.基于此,本文将研究如何缩放到合适比例,使模型和真实值之间的拟合误差最小.而获取最小比例需要在众多数值间枚举和组合,其过程与自然界中的多维搜索过程类似,而遗传算法正是解决这类问题的一种有效工具.
1.4 基于遗传算法的改进
遗传算法(Genetic Algorithm, GA)是一种模仿生物界进化机制的随机搜索算法,其基本思想为:通过编码组成初始群体后,对群体的个体按照它们对环境适应度(适应度评估)施加一定的操作,从而实现优胜劣汰的进化过程.通过一代又一代的搜索与优化,逐渐逼进最优解[18-19].
选用遗传算法的主要原因在于:(1)运行模式分布的分析实质是对于各VSP整数值的集计情况分析,属于离散函数,而遗传算法直接对结构对象进行操作,不存在求导和函数连续性的限制;(2)本节的主要目的在于获取拟合效果的最优值,尚无可参考的搜索过程规则,而遗传算法采用概率化的寻优方法,可自动获取和指导优化的搜索空间,自适应地调整搜索方向,从而无需再制定额外的规则.
本文所采用的遗传算法包括:初始种群构建、适用度计算、选择、交叉、变异等步骤.其中,适用度函数为该瞬时速度区间下,所有平均速度区间的误差加权平均值,本文中的适应度,即是该目标函数的最小值,如式(3)所示.
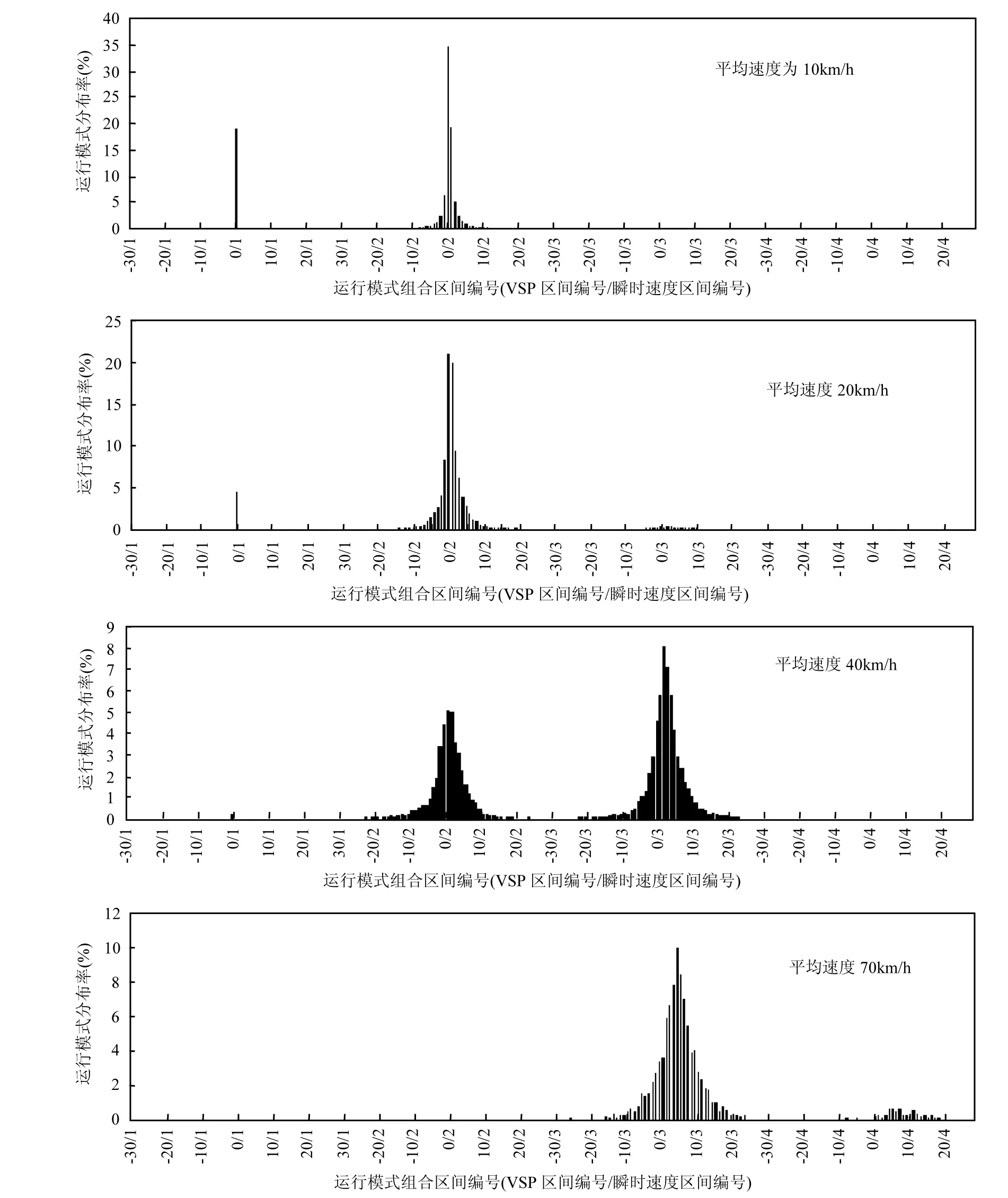
图3 不同平均速度下运行模式分布率Fig.3 Operating modes distribution under different average speed
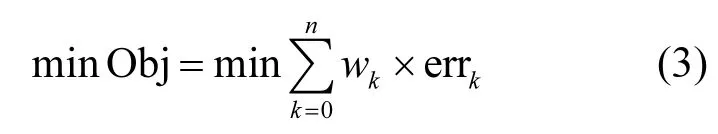
式中:Obj为目标函数;k为平均速度分组编号;wk为各平均速度组的出现频率,errk为该类在第k组平均速度的误差,其可通过式(4)~(6)计算.而各个平均速度区间的误差值,即是该平均速度下,所有VSP区间的高斯函数预测值与真实值之间的误差之绝对值.
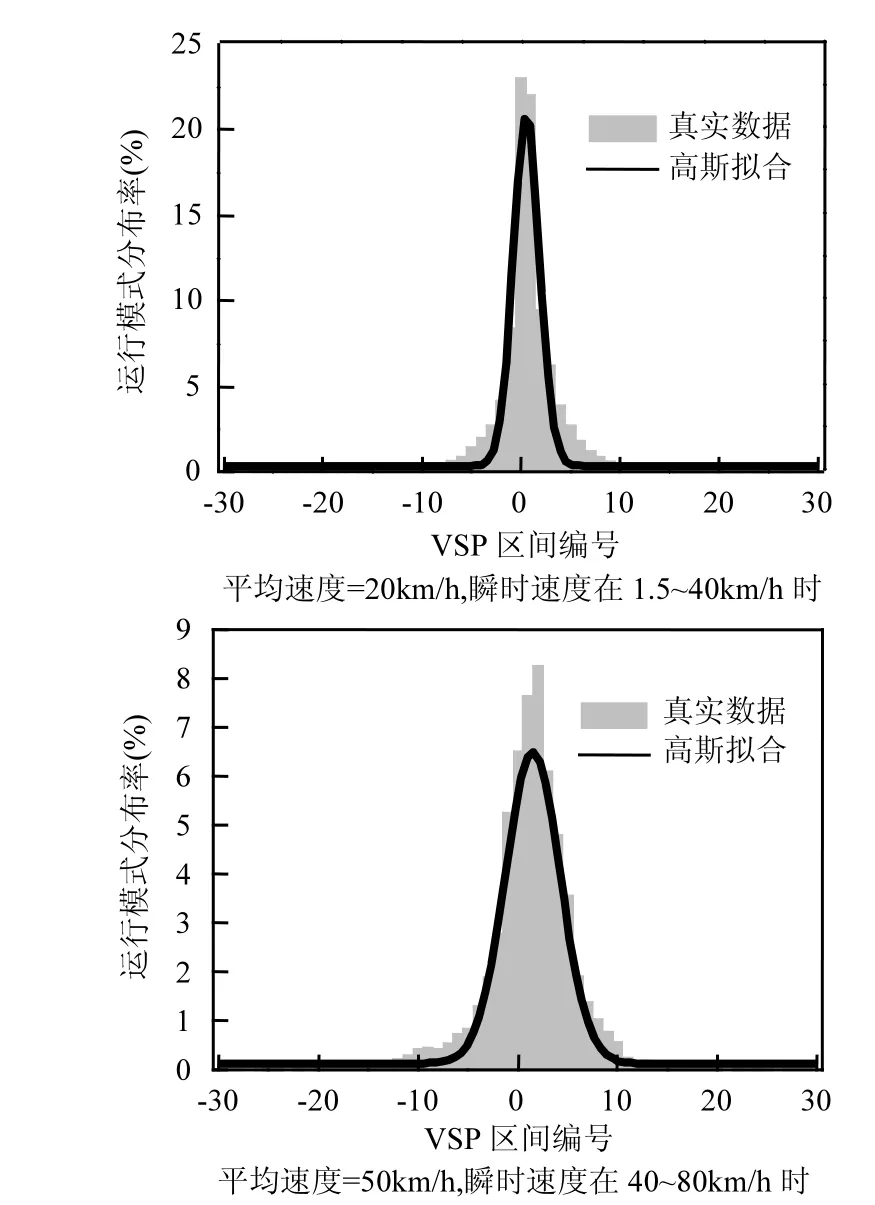
图4 高斯拟合问题和缺陷Fig.4 Drawbacks of the fitting curves by Gaussian function
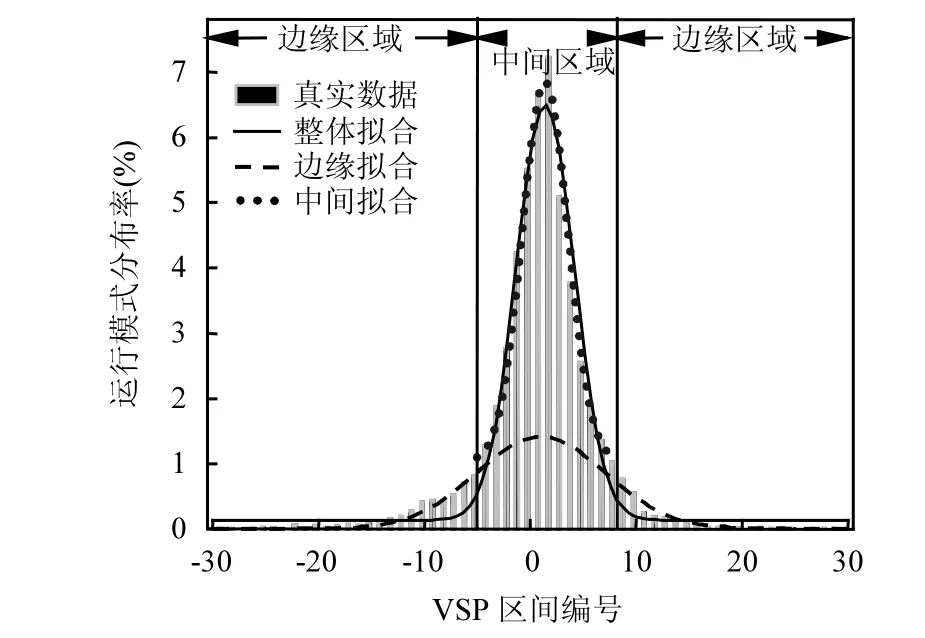
图5 模型改进区域划分Fig.5 Area division of improved model

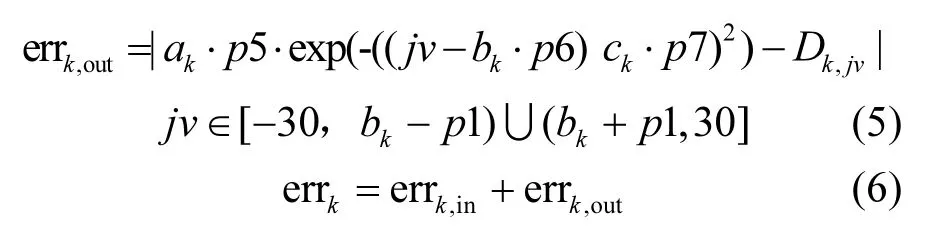
式中:errk为第k组平均速度的误差;下标in表示中间区域,下标 out表示边缘区域,e rrk,in、 errk,out为第k组平均速度中间和边缘区域的误差;jv为VSP区间编号; p2、p3、p4为中间区域的高斯参数a、b、c的缩放比例;p5、p6、p7为边缘区域的高斯参数a、b、c的缩放比例.
1.5 排放测算方法
建立运行模式分布模型的目标是对交通网络的排放进行测算,因此,有必要比较本文的模型、MOVES模型以及实际运行模式下的不同污染物排放情况.实际数据由1.1.1中的方法采集得到.对于应用MOVES模型测算时,继续沿用该模型中的排放计算方法,即采用平均速度对应行驶周期的方法获取,具体表1所示,当所遇到的平均速度不在列表中时,取临近两侧行驶周期所计算排放速率的加权平均值.
此外,为避免排放速率引起的误差,本文统一取 MOVES中,#10101202400000000轻型车的CO,HC,NOx排放速率,与各种模型方法获取的运行模式分布率结合,计算排放量,如公式(7)所示.
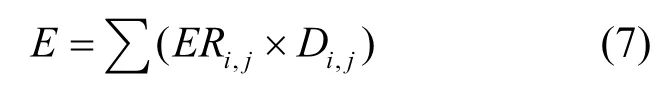
式中:E为某平均速度下的排放速率, i 瞬时速度区间编号; j 为VSP区间编号; ERi,j为瞬时速度(i)区间且VSP(j)区间的污染物(CO,HC,NOx)排放速率, Di,j为瞬时速度(i)区间且 VSP(j)区间的运行模式分布速率.
2 结果与讨论
2.1 瞬时速度0 ~1.5km/h区间模型
无论平均速度大小, VSP值均分布于 VSP∈[-0.5, 0.5] kw/t.如图6所示.
由图6可见,随着平均速度的上升,瞬时速度0~1.5km/h的样本量下降,当平均速度上升到47km/h时,该区间样本量减为0.观察其下降规律,发现快速路的样本量随平均速度上升呈现指数下降趋势,当平均速度大于 28km/h时,变化趋势趋于平缓.用指数函数对其进行拟合,如式(8)所示,其拟合优度为0.9647.

式中:x为平均速度;iv为瞬时速度区间编号;jv为 VSP区间编号;,分别为快速路和非快速路上,平均速度为x时,驾驶模式既处于瞬时速度iv区间,VSP分布又对应jv区间的概率.

图6 瞬时速度0 ~1.5km/h区间运行模式分布率与平均速度拟合Fig.6 Fitting curves of operating mode distribution vs. average speed in instantaneous speed 0 ~1.5km/h

表1 MOVES模型中不同平均速度对应的行驶周期Table 1 Description of the driving cycles of MOVES under different speed
2.2 瞬时速度1.5~40km/h、40~80km/h区间模型
2.2.1 基于遗传算法的运行模式分布模型 按 1.3的高斯拟合以及1.4的遗传算法改进后,模型进过250次迭代,适应度的演变情况如图7所示,不同区域的缩放比例如表2所示.各区间的误差平均值分别有了不同程度的减小,说明改进取得一定效果.此外,由改进参数可以看出,各区间在中心区域的高斯参数缩放比例改变均较小,说明改进前的高斯函数对中心区域的拟合效果较好.而边缘区域的高斯参数缩放比例较大,尤其是表示峰值的参数 a所对应的缩放比例,其值分别为0.3203和 0.2148,这说明边缘区域的值域远远低于中心区域,对所对应的缩放比例分别为 2.1922和 2.2667,其低峰值的高斯函数重新拟合效果显著.与此同时,边缘区域中表示“钟摆”宽度的高斯参数c扩大比例均接近100%,这说明原有的单个高斯函数无法拟合到较为外侧的边缘区域,从而导致结果产生较大误差.式中:x为平均速度; jv为VSP区间编号;

图7 各类区间的运行模式预测值误差趋势Fig.7 Trends of Estimated Errors in Different Bins


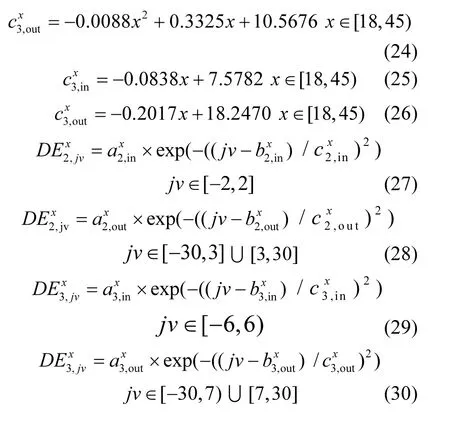

表2 改进模型的高斯参数缩放比例Table 2 Zoom factors of Guassion parameters of improved models
2.2.2 模型检验 通过遗传算法改进后,本节基于2.1.1中所计算得到的运行模式分布模型,针对不同等级道路各平均速度下的运行模式分布分别进行预测,并给出拟合优度 R2,如表 3所示.R2最高值为0.9942,最低值为0.7890,有78%的区间拟合优度高于0.85.
2.3 瞬时速度80km/h以上区间模型
由于瞬时速度80km/h以上区间所占比例非常小,再考虑我国城市道路条件以及限速规定,当瞬时速度在80km/h以上的数据中,有93%的样本点分布于平均速度 70km/h以上的区间中.因此,本文将平均速度为70km/h以上的所有样本集中,统一分析这部分样本在速度80km/h以上区间的VSP分布规律.继续用高斯函数拟合,其拟合函数如公式(31)

式中:x为平均速度,iv为瞬时速度区间编号,jv为 VSP区间编号,为快速路平均速度为x时,样本的瞬时速度值在iv区间且VSP值在jv区间的概率
该公式说明当平均速度大于 80km/h,将统一用本公式拟合其车辆运行模式的变化规律.此时,由于未划分平均速度,该瞬时速度区间的运行模式分布率不受平均速度影响,仅由 VSP决定.
对瞬时速度80km/h以上区间建模结果进行拟合优度检验,其R2分别为0.7.考虑到这部分数据量极小,在车辆运行模式中所占比例很低,不会对总体结果造成较大影响,故认为此拟合优度可以接受.

表3 改进后模型在不同平均速度下拟合优度Table 3 Goodness-of-fit of the improved models
2.4 模型排放测算
按1.5的思路,用实测、本模型和MOVES 3种方法进行排放测算,其情况如图8所示.
从图8中可以看出,本研究建立的模型预测结果比MOVES模型预测的结果更接近实际值,其中,本模型有 82.5%的区间平均排放率预测误差低于 MOVES,本模型的最大误差为 50.0%,而MOVES模型为304.2%.对HC排放而言,本模型预测误差在 0~17.9%之间,MOVES模型预测误差在1.2~67.6%之间,本模型有82.5%的区间平均排放率预测误差低于MOVES模型;对CO排放而言,本模型预测误差在1.2~50.0%之间,MOVES模型预测误差在0.6~304.2%之间,本模型有65%的区间平均排放率预测误差低于MOVES模型;对NOX排放而言,本模型预测误差在1.9~44.2%之间,MOVES模型预测误差在6.5~100.4%之间,本模型有 90%的区间平均排放率预测误差低于MOVES模型.
对于各平均速度而言,MOVES模型在平均速度为1km/h时,所对应行驶周期的排放速率误差估计最大,造成该现象的原因主要是:国内外不同的路网运行特征不同,怠速区间内,国内车辆的启停现象多于国外,因此,国内车辆在瞬时速度小于1.5km/h且VSP = 0的区间分布率远高于国外.而该部分的排放特征与其它区间存在显著差异,导致 MOVES模型在怠速区间的排放速率不能反映我国实情.
当平均速度处于低速区间时,本模型的测算误差大于 MOVES模型,例如:平均速度在 3~9km/h时,本模型测算的HC、CO、NOx的排放误差均高于MOVES模型.
此外,在真实值和本模型的预测值中,各污染物均呈现排放速率随平均速度的增加而增加的现象,且增长速率相对平缓.而在MOVES模型的预测值中,所有污染物的变化曲线均在48km/h和55km/h处产生两次突变.由于 MOVES模型中,采用平均速度邻近两侧行驶周期的加权平均值,来获取该平均速度下的运行模式分布,故上述突变由平均速度为55km/h时所对应的行驶周期所对应的分布模式造成.
由此可见,较之MOVES中默认行驶周期,本模型的预测结果可以更好地反映路段车辆在真实运行模式下所产生的排放.
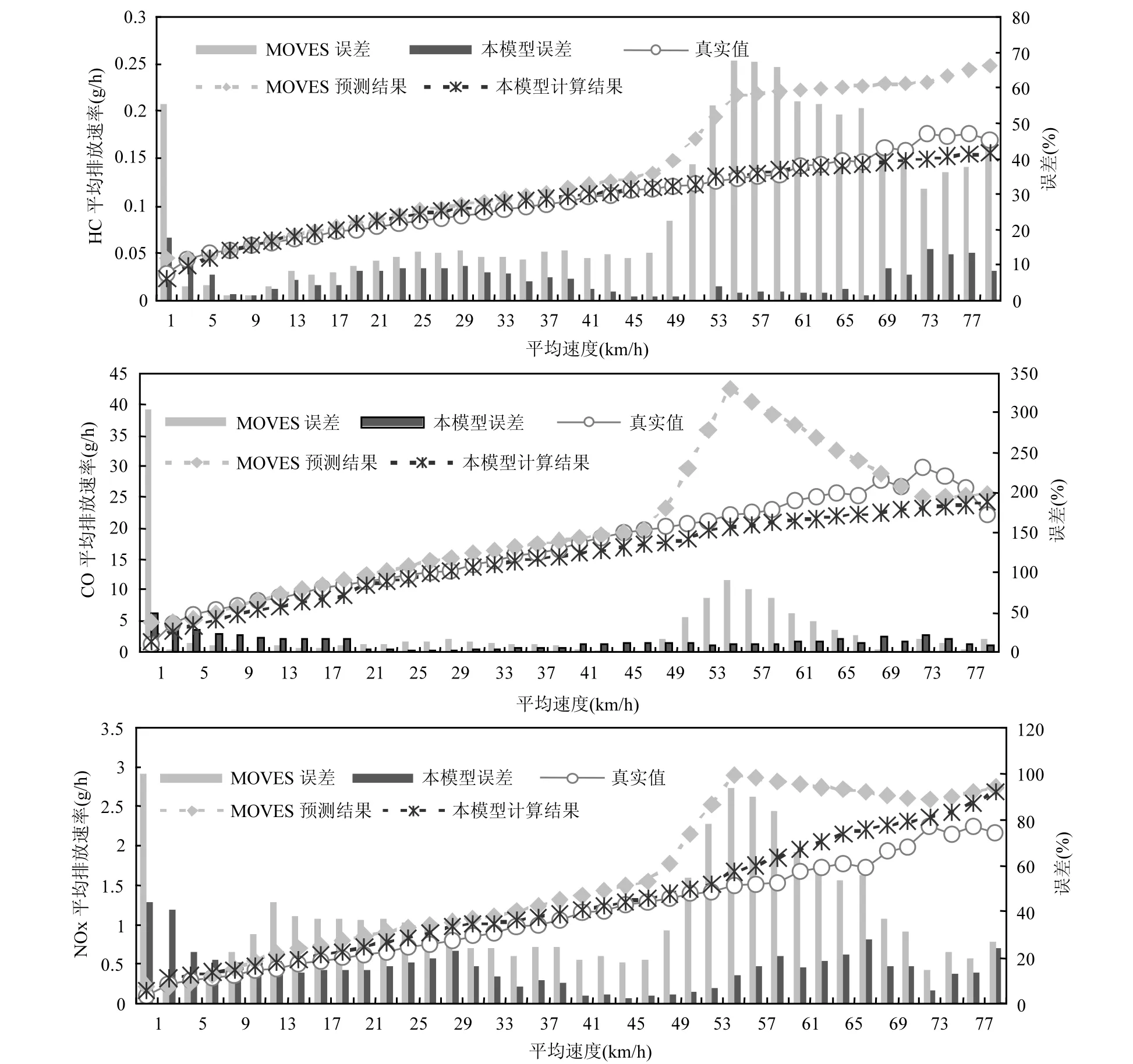
图8 不同运行模式模型预测的污染物平均排放速率Fig.8 Emission rates estimated by different models
3 模型应用
北京市实施了“每周少开一天车”的交通管理措施,具体内容为[20]:按车牌尾号每周停驶一天的车辆车牌尾号分为 5组,定期轮换停驶日.该政策的实施大大地削减了道路上机动车数量,有效地缓解了道路拥堵现状,降低了机动车油耗和尾气排放总量[21].本文利用建立的分布模型,对这一政策的节能减排效果进行量化和评价.
本文思路为:基于各路段每分钟的平均速度,利用 2.1~2.3所设计的路段运行模式分布模型,计算快速路上,不同平均速度下的各区间运行模式分布情况,进而对应MOVES中污染物在不同运行模式下排放速率,获取各路段每分钟的平均排放速率,最后计算排放总量.其中,采用式(8)~(31)分别计算平均速度对应的不同瞬时间速度区间的VSP的分布率,进而组合为各平均速度下的运行模式分布.
由于平均速度是本模型的主要输入参数,本文首先对限行前后车辆的平均速度进行获取,再由平均速度计算得到排放模式分布模型后,再结合路段长度、流量信息,则可计算各路段在高峰小时的排放总量,如式(32).需要说明的是,本文假设路网中运行车辆均为轻型汽油车,而不考虑其它车型的排放状况. 在高峰小时内,假设每小时内流量均匀分布.各路段不同污染物的排放总量如图9所示.
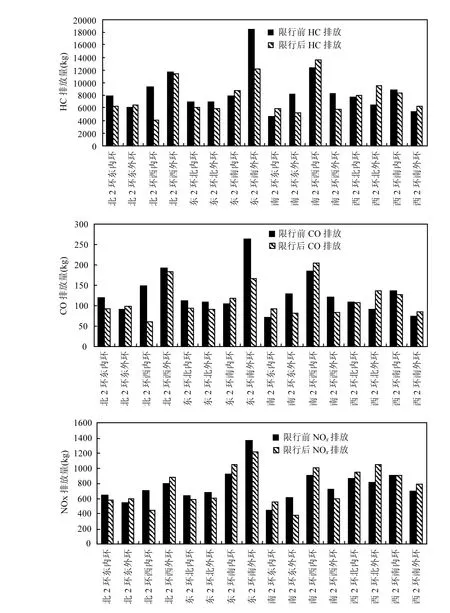
图9 限行前后各路段污染物排放对比Fig.9 Comparison of emissions on each link before and after vehicle restriction

式中:EMie为污染物ie的排放总量;J表示研究时间范围内的时间片段集合;je为研究范围内的时间片段;Volje为je时间段内的流量;表示污染物ie在时间片段je内平均排放率,g/h;L为路段长度,km;vje为je时间内的平均速度,km/h.
由图9可见,就总体而言,由于限行后道路流量减少7.9%,加之平均速度提高至30.56km/h,该速度较现行前提高了4.5km/h,提高比例为13.8%,因此,各种污染物有了不同程度的减少.限行后二环路高峰小时 HC排放 1.24kg,较限行前减少9.58%;限行后二环路高峰小时CO排放182.80kg,较限行前减少 11.41%;限行后二环路高峰小时NOx排放11.18kg,较限行前减少0.49%.对具体道路而言,北二环西段内环限行后减排量最明显,HC、CO、NOx分别减排55.75%、59.03%、36.74%,其下降的主要原因是该路段上限行后流量减少了35.48%.此外还有北二环东内环的HC、CO、NOx排放、北二环西外环的HC、CO排放等56.25%的路段对应污染物在限行后有所减少.而西二环北外环在限行后,HC、CO、NOx反而分别增加了45.34%、48.85%、29.06%,主要由于该路段流量在限行后增加了24.98%,此外还有东二环南内环的HC、CO、NOx等43.75%的路段对应污染物在限行后也有所增加.从各路段限行前后的流量、速度、各污染物排放分析可知,导致限行后污染物排放总量改变的主要因素是路段上流量的变化,而平均速度的改变也会在一定程度上引起排放的波动.
4 结论
4.1 本文基于遗传算法,建立了用于路网污染物排放测算的运行模式分布模型,实现了由平均速度计算排放模型测算所需的运行模式分布的数学方法,有利于动态评价交通路网的排放效果.
4.2 本模型与实际运行模式拟合的 R2较高,瞬时速度 0~1.5km/h,1.5~40km/h,40~80km/h的 R2达到在0.7890以上;瞬时速度80km/h以上区间的R2达到在0.700以上.
4.3 使用本模型和MOVES模型测算路网排放,三种污染物综合而言,本研究建立的模型预测结果比MOVES模型预测的结果更接近实际值:本模型有 82.5%的区间平均排放率预测误差低于MOVES,本模型的最大误差为50.0%,而MOVES模型为304.2%.可见本模型比MOVES更适合评价路网动态排放.
4.4 使用本模型对北京市在限行前后的污染物排放进行分析,对二环整体而言,限行后HC、CO、NOx均有所降低,但由限行后部分道路的流量增加,导致这部分路段的污染物排放反而有所上升.
[1] U.S. Environmental Protection Agency (EPA). Motor vehicle emission simulator highway vehicle implementation (MOVESHVI) demonstration version: Software design and reference manual draft. publication EPA420-P-07-001 [R]. Washington D.C., Office of Transportation and Air Quality, U.S. Environmental Protection Agency, 2007.
[2] Barth M, An F, Younglove T, et al. Development of a comprehensive modal emission Model-Final report [R] Washington D.C., Transportation Research Board National Research Council. April 2000.
[3] Ahn K, Rakha H, Trani A, et al. Estimating vehicle fuel consumption and emissions based on instantaneous speed and acceleration levels [J]. Journal of Transportation Engineering. 2002,128(2):182-190.
[4] Davis, N, James L, Mauricio O, et al. Development and application of an international vehicle emissions Model [J]. In Transportation Research Record: Journal of the Transportation Research Board, 2005,1939:157–165.
[5] 郝艳召,宋国华,邱兆文,等.基于浮动车数据的机动车排放实时测算模型 [J]. 中国环境科学, 2015,35(2):396-402.
[6] 陈长虹,景启国,王海鲲,等.重型机动车实际排放特性与影响因素的实测研究 [J]. 环境科学学报, 2005,25(7):870-878.
[7] 潘汉生,陈长虹,景启国,等.轻型柴油车排放特性与机动车比功率分布的实测研究 [J]. 环境科学学报, 2005,25(10):1306-1313.
[8] 王岐东,姚志良,霍 红,等.中国城市轻型车的排放特性 [J]. 环境科学学报, 2008,28(9):1713-1719.
[9] 曲 亮,李孟良,高佳佳,等.基于浮动车数据的机动车排放实时测算模型 [J]. 中国环境科学, 2015,35(2):396-402.
[10] Zhang Y Y, Chen X, Zhang X, et al. Assessing Effect of traffic signal control strategies on vehicle emissions journal of transportation systems engineering and information technology,2009,9(1):150-155.
[11] 杨 方.基于 PEMS的轻型车热稳状态下微观尾气排放模型[D]. 北京:北京交通大学, 2005.
[12] Liu H, He K B, Lents J. A methodology for developing a micro-emission model based on on-board heavy duty truck tests in China [C]//87th Transportation Research Board Annual Meeting CD-ROM, Washington, D.C., USA, 2008.
[13] 陈 琨.微观交通仿真与尾气评估 [D]. 北京:北京交通大学, 2003.
[14] Lents J, Walsh M, K. He, et al. Handbook of air quality management [EB/OL]. http://www.aqbook. org/read/? page= 86, 2009.
[15] Frey H C, Rouphail N M, and Zhai H. Speed- and facilityspecific emission estimates for on-road light-duty vehicles on the basis of real-world speed profiles [J]. Transportation Research Record: Journal of the Transportation Research Board, 2006,1987:128–137.
[16] 宋国华,于 雷.城市快速路上机动车比功率分布特性与模型[J]. 交通运输系统工程与信息, 2010,10(6):133-140.
[17] Jose L J Understanding and quantifying motor vehicle emissions with vehicle specific power and TILDAS remote sensing [D]. Cambridge US: Massachusetts Institute of Technology, 1999.
[18] Jong K A D. An analysis of the behavior of a class of genetic adaptive systems [D], U.S: University of Michigan, 1975.
[19] Goldberg, D E. Genetic algorithms in search, optimization, and machine learning [M]. U.S: Addison-Wesley Publishing. Co. Inc., 1989.
[20] 北京市人民政府.北京市人民政府关于实施交通管理措施的通告 [R]. 北京市人民政府, 2009.
[21] 刘 娟.基于实时数据修正的尾气排放因子获取技术与方法实现 [D]. 北京:北京交通大学, 2006.
GA-based approach to modeling operating mode distributions and estimating emissions.
XU Yao-fang1*, YU Lei2,3, SONG Guo-hua3(1.School of Traffic and Transportation, Chongqing Jiaotong University 400074, China;2.Texas Southern University, Texas 77004, USA;3.Beijing Jiaotong University, Beijing 100044, China). China Environmental Science, 2016,36(12):3548~3559
In view of the widely available data of the average speed in traffic systems and the parameter of operating mode distribution needed in emission models, a model was developed for generating operating mode distribution based on the average speed. Genetic Algorithm was used further for optimizing the model. After a comparison with the real-world data, it was found that the average emission rates estimated based on the proposed model exhibited less errors than those estimated based on MOVES in 82.5% of the speed bins. The highest error based on the proposed model was 50% while 304.2% based on MOVES. Finally, the proposed model was used to estimate emissions in Beijing for pre- and after- the implementation of the vehicle restriction policy. It was found that the 2nd Ring Road has experienced a reduction of total emissions of HC, CO, NOxby 9.58%, 11.41%, 0.49% respectively. Compare with the test values, the R2with the model were higher than 0.700 and errors of the model were much lower than that of the MOVES. Further a modal application was proposed, which can calculate the traffic exhaust emissions of dynamic network.
operating mode distribution;emission evaluation;average speed;genetic algorithm
X511
A
1000-6923(2016)12-3548-12
胥耀方(1984-),女,重庆人,副教授,博士,主要从事交通环境研究.发表论文14篇.
2016-04-17
国家自然科学基金资助项目(51578052),重庆市自然科学基金(ctcs2013jcyjA00015),重庆市教委资助项目(KJ1400328)
* 责任作者, 副教授, 335339053@qq.com
