基于改进人工鱼群算法的DGPS整周模糊度快速固定

王跃钢，王 乐，腾红磊，张兆龙

（火箭军工程大学 304教研室，西安 710025）

基于改进人工鱼群算法的DGPS整周模糊度快速固定

王跃钢，王 乐，腾红磊，张兆龙

（火箭军工程大学 304教研室，西安 710025）

为提高DGPS整周模糊度的搜索效率，将改进人工鱼群算法引入模糊度固定解搜索环节。在解算中首先根据GPS双差载波相位观测方程，利用卡尔曼滤波估计模糊度浮点解，针对短基线解算问题，以基线长度为约束确定模糊度搜索范围，进而采用LLL降相关算法对模糊度浮点解作降相关处理，最后利用附加整数约束的改进人工鱼群算法搜索整周模糊度固定解。算例分析结果表明，在与遗传算法的100次对比实验中，改进人工鱼群算法搜索平均用时1.6617 s，比遗传算法缩短2.4987 s，算法搜索速度更快，搜索效率明显提高。算法的模糊度搜索成功率为 92%，高出遗传算法 9%，搜索成功率得到有效提升。因此，与遗传算法相比，改进人工鱼群算法能够更为快速地得到整周模糊度固定解，且具有更高的搜索效率和成功率。

DGPS；整周模糊度；LLL降相关算法；改进人工鱼群算法

航空重力测量的一项重要内容是利用DGPS技术高精度解算载体加速度，在采用双差载波相位观测量时，整周模糊度的快速固定是关键[1]。通常模糊度的解算按如下步骤进行：首先得到忽略整数约束的模糊度浮点解及其协方差矩阵，构造搜索空间；进而针对浮点解间的相关性问题，对浮点解作降相关处理；最后运用搜索算法搜寻得到整周模糊度固定解[2-4]。近年来，国内外学者积极探索模糊度解算方法，在改善病态性、改进降相关效果、提高搜索效率等方面展开研究[5-8]，特别是在搜索算法方面采用了现代启发式算法，如遗传算法、蚁群算法和粒子群算法等[9-11]。为进一步提高搜索效率，本文将采用改进人工鱼群算法搜索模糊度固定解。

人工鱼群算法（Artificial Fish Swarm Algorithm,AFSA）是李晓磊提出的一种现代启发式寻优算法，用于解决组合优化问题。该算法的基本原理是通过构造人工鱼模拟鱼的觅食、聚群和追尾行为，从单条鱼的基本行为开始，通过鱼群中各个体的局部寻优，达到全局最优值在群体中凸显的目的，具有并行、高效和较强的取得全局最优解的能力[12-13]。

本文针对DGPS整周模糊度的快速固定问题，将人工鱼群算法引入整周模糊度的搜索环节，并针对问题特性对人工鱼群算法作整数约束改进，在提高搜索效率的同时保证了算法的收敛性和有效性。

1 卡尔曼滤波滤波估计模糊度浮点解

在DGPS定位技术中，参考站i、j(GPS双频接收机)相对于卫星k、l的GPS双差载波相位L1和L2波段观测方程为[14]

式中：1Φ、2Φ分别表示L1和L2波段载波相位伪距观测量；ρ表示接收机与卫星间的欧氏距离；、分别表示L1和L2波段的电离层延迟；T表示对流层延迟；λ为载波波长；N为整周模糊度；ε为观测噪声。

参考站的坐标精确已知，通过卡尔曼滤波可实时估计基线向量、对流层延迟、电离层延迟和载波相位模糊度实数解。卡尔曼滤波模型表示为

式中：Xk为状态向量；kΦ为一步转移矩阵；Lk为观测向量；Hk为量测矩阵；Wk、Vk分别为状态噪声和量测噪声；Qk、Rk分别是其相应的协方差阵。

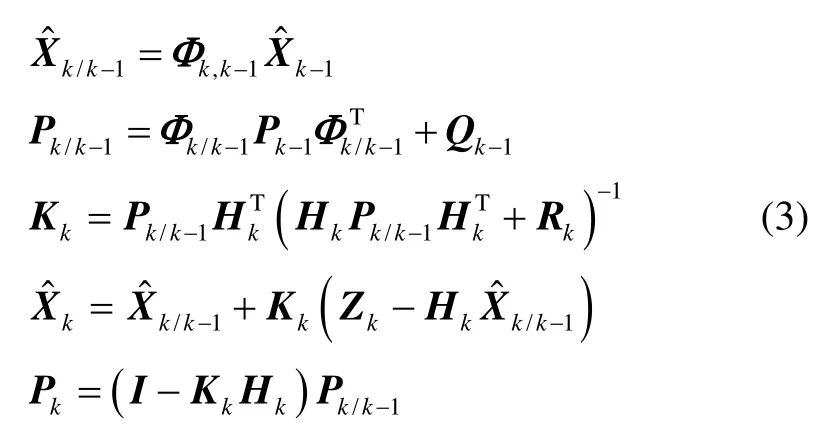
整周模糊度的固定解N并不能简单地通过在浮点解ˆN附近取整数值得到，需要由上述浮点解根据一定准则通过整数约束搜索得到，因此，可通过使下面二次型目标函数最小来求解整周模糊度的固定解：

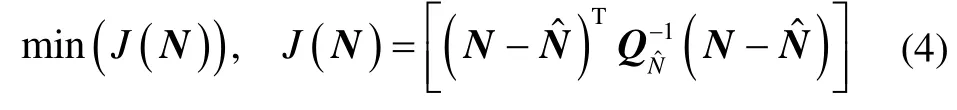
为解算式(4)，需首先确定一个整数向量集合，然后从中根据目标函数最小原则搜索出整周模糊度的固定解。该整数向量集合即为整周模糊度的搜索空间。在DGPS短基线定位应用中，采用基线长度作为约束条件，构造搜索空间如下：

2 LLL模糊度降相关算法

首先对协方差阵QˆN进行Cholesky分解，即QˆN=，其中的行向量记为。对进行整数Gram-Schmidt正交变换：

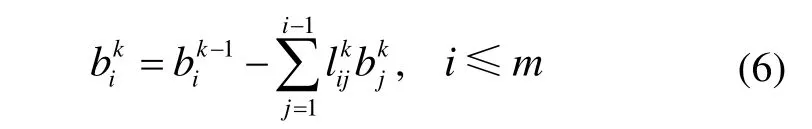
式中：

3 改进人工鱼群算法求解整周模糊度

为了更快速准确地求解目标函数(4)的最小值，进而正确固定整周模糊度，引入人工鱼群算法解决该问题。算法基本定义如下：

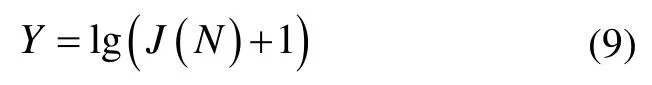
人工鱼i和j的间距表示为

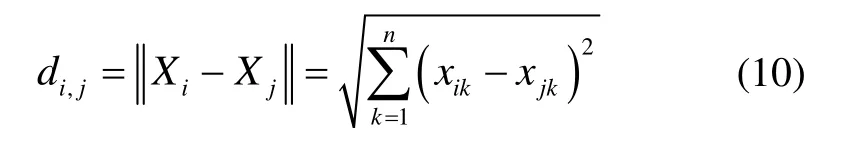
算法执行过程中，人工鱼在水中随机游动，通过感知能力确定水中的食物浓度，并实施觅食、聚群和追尾行为，用公告板记录最优鱼的状态，通过算法迭代中状态的不断更新实现寻优。对于模糊度固定解搜索问题，由于模糊度搜索空间属于整数域，需要对人工鱼群算法作整数约束改进，改进后人工鱼执行觅食行为的一步状态转移方程表示为

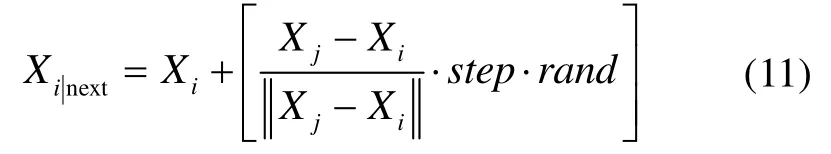
式中：Xi表示人工鱼当前状态；Xj表示感知范围内的另一状态；［·］表示取整算子；rand表示［0,1 ］内随机数。聚群和追尾行为的一步状态转移方程与式(11)类似，不作赘述。

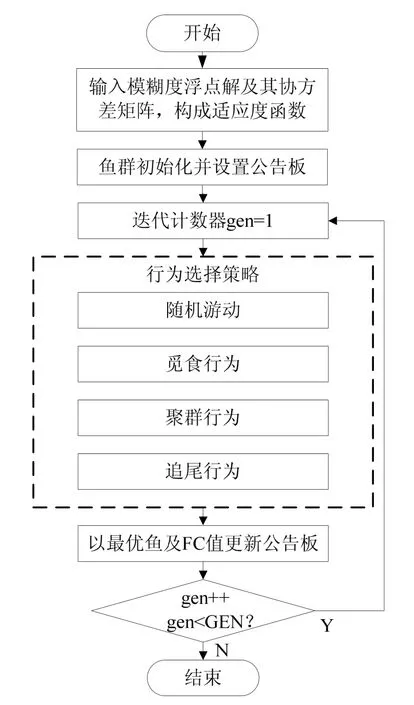
图1 改进人工鱼群算法流程图Fig.1 Flowchart of the improved artificial fish swarm algorithm

鉴于以上算法定义与行为描述，将搜索整周模糊度的改进人工鱼群算法流程描述如图1所示。

4 仿真实验与分析

采用本文提出的方法对DGPS整周模糊度进行快速固定的处理流程如图2所示。

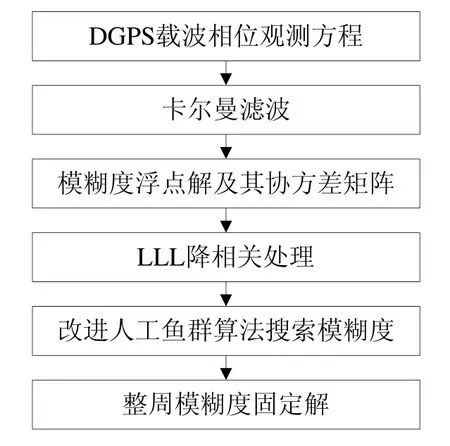
图2 基于IFASA快速固定DGPS整周模糊度流程图Fig.2 Flowchart of fast fixing the DGPS integer ambiguity based on the improved artificial fish swarm algorithm

为验证该方法的有效性，采用文献[2]中的经典算例进行仿真验证，选取模糊度浮点解及其协方差矩阵为

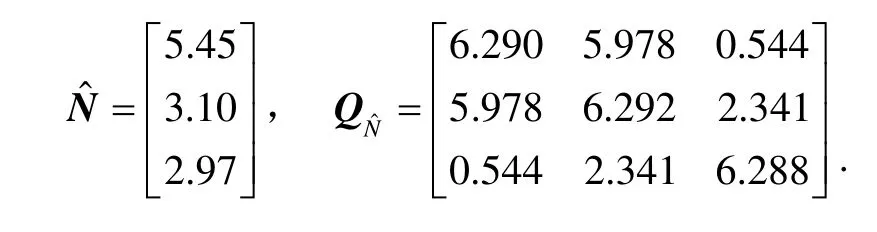
从上述协方差矩阵可以看出，各个维度上的模糊度间具有较强的相关性，将严重影响搜索效率，并可能导致搜索失败。因此本文采用LLL降相关算法对协方差阵进行处理，降相关后的浮点解及其协方差阵为：

可见，与原始协方差阵相比，降相关后的协方差阵更接近对角阵，说明降相关的过程使各维模糊度间的相关性明显降低，从而使对应的食物浓度函数的函数特性也发生了变化。

图3反映了降相关前后食物浓度函数值在三维整周模糊度空间中的变化。图3中颜色的变化代表食物浓度函数值的变化，由于算例中的食物浓度函数是超维函数，难以在三维空间中直观观察其变化程度，为方便研究，分别取三维模糊度中任意两维模糊度对降相关前后食物浓度函数的分布情况进行研究，如图4所示。

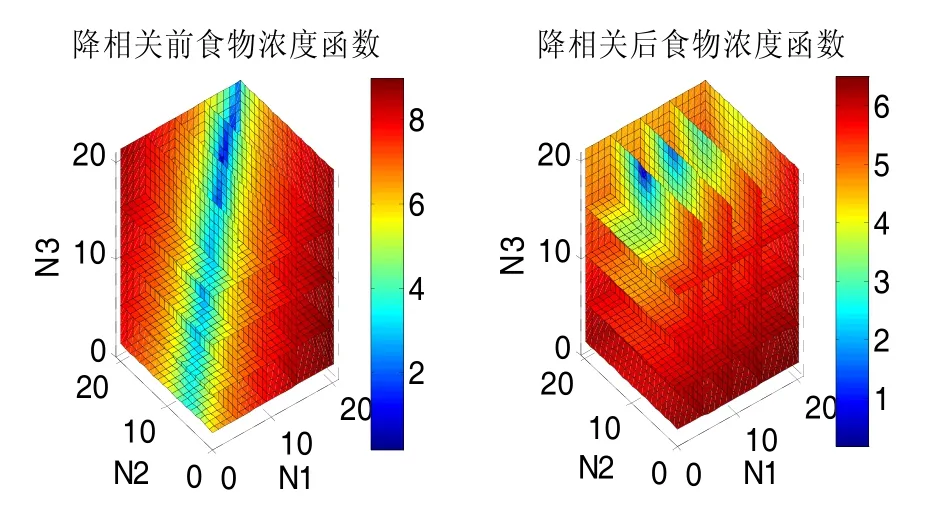
图3 降相关前后食物浓度函数Fig.3 FC functions before and after decorrelation

图4 降相关前后两两模糊度间的食物浓度函数Fig.4 Food concentration functions of two ambiguities before and after decorrelation

由图3、图4可以看出，相对于原食物浓度函数存在多个局部极值点的情况，降相关后的食物浓度函数仅有一个最优解对应着整周模糊度固定解，能够避免人工鱼群算法陷入局部最优解，有助于提高算法的效率和搜索正确率，使搜索过程快速收敛到全局最优解。

采用本文提出的改进人工鱼群算法在降相关后搜索空间中搜索整周模糊度固定解，算法的参数设置为：鱼群规模，迭代次数，人工鱼每次移动的最大试探次数，人工鱼的感知距离，拥挤度因子 δ= 0.618，人工鱼移动的最大步长step=2。为检验算法性能，分别采用本文算法和遗传算法在相同条件下分别进行了100次仿真实验，遗传算法的种群大小设为50，最大进化代数设为 100。实验结果表明，利用改进人工鱼群算法，有 92次得到全局最优解，搜索正确率为92%，高于遗传算法83%的搜索正确率。算法具有更高的搜索可靠性，这也反映出改进人工鱼群算法更好地解决了全局搜索和局部搜索的问题，在搜索中更易跳出局部极值。进一步对比改进人工鱼群算法和遗传算法在100次实验中收敛到最优解的收敛代数，如图5所示。

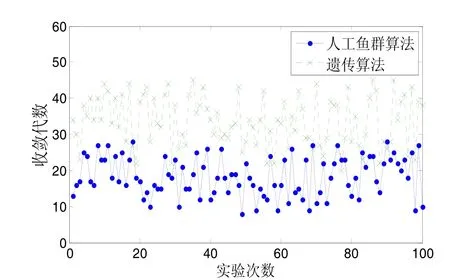
图5 两种算法收敛代数对比Fig.5 Comparison on two algorithms for convergence algebra

由图5可知，人工鱼群算法可以比遗传算法更快地收敛到全局最优解，采用人工鱼群算法，平均收敛代数为18.45，按四舍五入取整，算法平均在搜索18代后收敛，则搜索的空间为900（18× 50），占问题空间（ 213）的9.72%，算法搜索平均用时1.6617 s；遗传算法的平均收敛代数为 33.7，搜索的空间为 1700（34× 50），占问题空间（ 213）的 18.36%，算法搜索平均用时4.1604 s。实验结果表明，与遗传算法相比，人工鱼群算法具有更高的搜索效率。

图6和表1给出了整周模糊度一次解算中食物浓度函数Y的变化过程。

综合图6、图7和表1可以看出，在人工鱼群算法的一次解算中，鱼群在迭代11次后收敛到了全局最优解，收敛速度较快，且收敛后食物浓度函数值未再发生波动，稳定性较高，随着迭代次数的增加，鱼群逐渐靠拢到全局最优解附近。这也说明算法达到了全局寻优的目的，并且更加高效、可靠。

图7给出了迭代前后鱼群的空间分布情况。

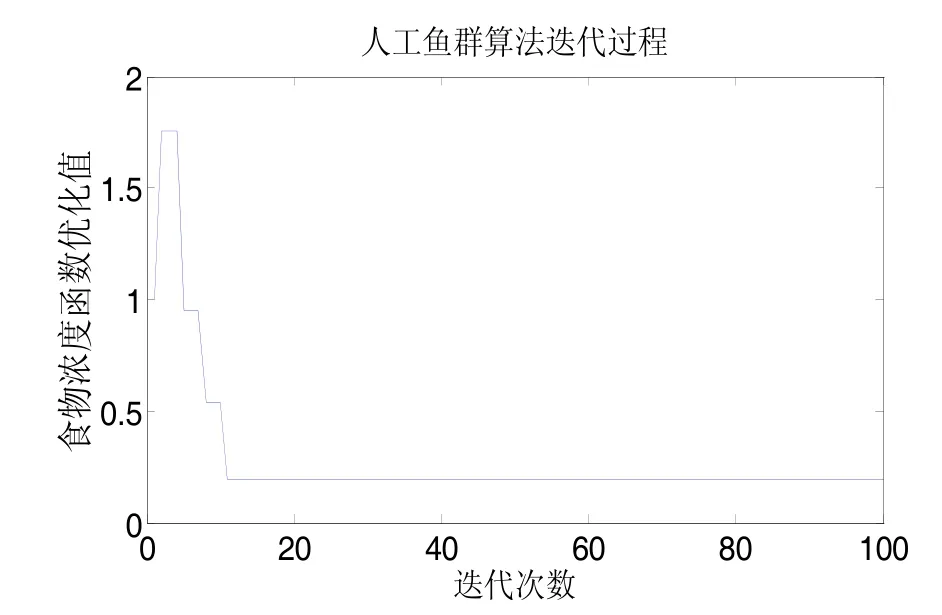
图6 迭代过程中食物浓度值的变化Fig.6 Changes of food concentration in iterative process

表1 迭代过程中最优解的演变Tab.1 Changes of optimal solution in iterative process

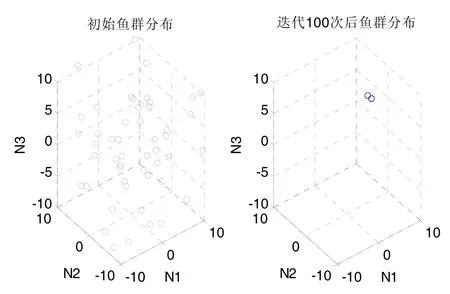
图7 鱼群空间分布变化Fig.7 Spatial distribution of fish swarm

5 结 论

本文将改进人工鱼群算法引入DGPS整周模糊度的解算问题。在降相关的基础上，通过人工鱼群算法改善搜索性能，提高搜索效率和成功率，达到更快速、准确地解算整周模糊度的目的。通过算例分析可知，与遗传算法相比，本文算法的搜索成功率优于遗传算法，且搜索效率高，耗时短。

然而，关于这种方法还有许多问题值得进一步探讨与研究，如研究通过自适应调整算法参数提高搜索效率，通过约束方程进一步缩小算法初始搜索范围，进一步提高算法搜索全局最优解能力提高成功率等等，这些都是可以再深入研究的课题。

（References）：

[1]Xu Ying, Ji Shengyue, Chen Wu. A new ionosphere-free ambiguity resolution method forlong-range baseline with GNSS triple-frequency signals[J]. Advances in Space Research, 2015, 56: 1600-1612.

[2]de Jorge P, Tiberius C. The LAMBDA method for integer ambiguity estimation: implementation aspects[R]. Delft:Delft University of Technology, 1996.

[3]Li Bo-feng, Verhagen S, Teunissen P J G. GNSS integer ambiguity estimation and evaluation: LAMBDA and Ps-LAMBDA[C]//2013 Proceedings of China Satellite Navigation Conference. Wuhan, China, 2013: 291-301.

[4] 李豹, 许江宁, 曹可劲, 等. 改进 LAMBDA 算法实现单频 GPS 整周模糊度快速解算[J]. 中国惯性技术学报, 2013, 21(3): 365-368.Li Bao, Xu Jiang-ning, Cao Ke-jin, et al. Fast resolution of single frequency GPS integer ambiguity realized by improved LAMBDA algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 365-368.

[5]段荣, 赵修斌, 庞春雷, 等. GPS快速定位中相位模糊度动态解算的一种正则化方法[J]. 中国惯性技术学报.2015, 23(5): 624-630.Duan Rong, Zhao Xiu-bin, Pang Chun-lei, et al. Regularization approach for dynamic resolution of phase integer ambiguity in GPS rapid positioning[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 624-630.

[6]邓健, 王胜利, 陈润静. GNSS网络实时动态模糊度解算病态性解决策略[J]. 中国惯性技术学报, 2016, 24(1):14-19.Deng Jian, Wang Sheng-li, Chen Run-jing. Resolving strategies for ill-posed equation in ambiguity resolution of GNSS network real-time kinematics[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 14-19.

[7]范龙, 翟国君, 柴洪洲. 模糊度降相关的整数分块正交化算法[J]. 测绘学报, 2014, 43(8): 818-826.Fan Long, Zhai Guo-jun, Chai Hong-zhou. Ambiguity decorrelation with integer block orthogonalization algorithm[J]. Acta Geodaetica et Catographica Sinca, 2014,43(8): 818-826.

[8]王胜利, 王庆, 潘树国, 等. 基于抗差估计的网络RTK基站双差模糊度检验与修正方法[J]. 中国惯性技术学报, 2012, 20(6): 705-714.Wang Sheng-li, Wang Qing, Pan Shu-guo, et al. Double integer ambiguities test and repair method for network RTK base stations based on robust estimation[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 705-714.

[9]徐定杰, 刘明凯, 沈锋, 等. 基于自适应遗传算法的DGPS整周模糊度快速解算[J]. 航空学报, 2013, 34(2):371-377.Xu Ding-jie, Liu Ming-kai, Shen Feng, et al. Fast DGPS integer ambiguity resolution using adaptive genetic algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(2): 371-377.

[10]S Jazaeria, A R Amiri-Simkooeib, M A Sharifia. Fast GNSS ambiguity resolution by ant colony optimisation[J].Survey Review, 2013, 330(45): 190-196.

[11]Skvortsov A N. Estimation of rotation ambiguity in multivariate curve resolution with charged particle swarm optimization[J]. Journal of Chemometrics, 2014, 28(10): 727-739.

[12]王庭军, 高延滨, 李光春. 利用人工鱼群算法对光纤陀螺随机漂移建模[J]. 中国惯性技术学报, 2012, 20(3):358-362.Wang Ting-jun, Gao Yan-bin, Li Guang-chun. FOG random drift modeling by artificial fish swarm algorithm[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 358-362.

[13]Peng Yong. An improved artificial fish swarm algorithm for optimal operation of cascade reservoirs[J]. Journal of Computer, 2011, 6(4): 740-746.

[14]Chang-Ki Hong, Chi Ho Park, Joong-hee Han, et al.Medium to long range kinematic GPS positioning with position-velocity-acceleration model using multiple reference stations[J]. Sensors, 2015, 15: 16895-16909.

DGPS integer ambiguity fast fixation based on improved artificial fish swarm algorithm

WANG Yue-gang, WANG Le, TENG Hong-lei, ZHANG Zhao-long
(Unit 304, Rocket Force University of Engineering, Xi’an 710025, China)

In order to improve the search efficiency of DGPS integer ambiguity, an improved artificial fish swarm algorithm (IAFSA) is introduced into the search of the integer ambiguity. Firstly, according to the DD GPS carrier phase observation equation, a Kalman filter is used to estimate the ambiguity floating-point solution. For the solution problem of short baseline, the range of ambiguity is determined with the constraint of baseline length. Then the LLL algorithm is used into the ambiguity decorrelation problem. Finally, the IAFSA with integer constraints is used to search the fixed solutions of integer ambiguity. The results of an example show that the average searching time of IAFSA is 1.6617 s, which is 2.4987 s shorter than that of the genetic algorithm(GA) in 100 experiments. The success rate of ambiguity search is 92%, which is 9% higher than that of the GA, showing that the IAFSA can get the fixed ambiguity solution more quickly, and has higher search efficiency and reliability.

DGPS; integer ambiguity; LLL decorrelation algorithm; improved artificial fish swarm algorithm

P228.4

A

1005-6734(2016)05-0619-05

10.13695/j.cnki.12-1222/o3.2016.05.011

2016-07-28；

2016-09-20

国防预研（403050202）

王跃钢（1958—），男，教授，博士生导师。E-mail: wangyueg@163.com