Fast alignment algorithm with order-reduced filter for SINS

WANG Rong-ying, LIU Wen-chao, BIAN Hong-wei, GAO Xin(. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, China;. Unit 9550 of PLA, Dalian 606, China)

Fast alignment algorithm with order-reduced filter for SINS

WANG Rong-ying1, LIU Wen-chao2, BIAN Hong-wei1, GAO Xin1
(1. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, China;2. Unit 91550 of PLA, Dalian 116026, China)

The initial alignment method of SINS (Strapdown Inertial Navigation System) with measurements of inertial components can efficiently improve the alignment speed, but it has large amount of filtering calculation, its system noise and measurement noise are correlated, and its measurements contain high frequency noise which can affect the filtering accuracy. To solve these problems, an order-reduced filter for fast alignment of the SINS is proposed, whose dimensions of state equation is reduced by removing no observable states and the reasonable selection, and the measurement equation is deduced.Then the state variables can be estimated by noise-related Kalman filter with the original information preprocessed by low-pass filter. Theory analysis and test results show that the new method can improve the convergence speed of horizontal misalignments by 90%, reduce the calculation amount by 83.33%, and effectively suppress the effect of the high frequency noise.

strapdown inertial navigation system; initial alignment; order-reduced filter; low-pass filter;observability

The aim of initial alignment of SINS is to obtain the coordinate transformation matrix from body frame to navigation frame and conduct the misalignment angles to zero or as small as possible[1]. The initial alignment of SINS on stationary base is generally divided into two phases: the coarse and fine alignment. In the former phase, an initial attitude matrix is roughly calculated by analytic coarse alignment and one-step correcting coarse alignment with the measurement information of the inertial components; in the latter phase, a relatively precise initial attitude matrix is obtained by estimating misalignment angles with filtering method, based on the system state equations and observation equations constructed[2].

In the conventional methods for fine alignment of SINS, the velocities are usually used as the observed information and it takes a long time to estimate the misalign-ment angles. On the basis of the conventional method,introducing the equivalent outputs of accelerometers can efficiently improve the convergence rate of horizontal misalignment angles. The convergence rate of azimuth misalignment angles and equivalent constant drifts of azimuth gyro can also be improved by introducing equivalent gyro outputs. Making full use of inertial measurement components’ information can efficiently improve the speed of initial alignment[3-8]. However, with more observations, the dimensions of alignment models and the amount of computation significantly increase.Moreover, system noise and measurement noise will relates to each other and high frequency noise in measurement value can affect the accuracy of filtering.

To solve these problems, this paper constructs an order-reduced model for rapid initial alignment of SINS by selecting states and referring the idea of one-step correcting coarse alignment. And Kalman filtering with noise-related is applied to estimate the system states on the condition of low-pass filter procession for the original outputs of inertial components.

1 Design of order-reduced model for SINS initial alignment

1.1 State equation

The bias of accelerometers and the constant drift of equivalent east gyro are all unobservable in both of the conventional initial alignment model and the model with observation information of inertial components. Based on the SINS error model on stationary base[9-10], the unobservable states and the rest will be decoupled. Let the states vector is X:

And the five-dimension state equation is as follows:

Where

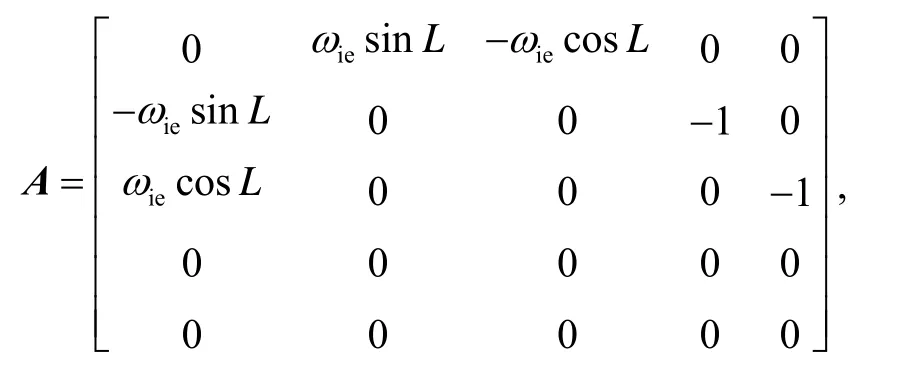
ωieis the earth rate; L is the local latitude; g is the acceleration of gravity; φ is the misalignment angle; ε is the gyro drift and ▽ is the accelerometer bias; wgare the projections of three gyro random noise in the navigation coordinate of three axes. The subscripts E, N and U denote the respective body axis.

Since ▽E, ▽Nand Eε have not been estimated, in practical application, the estimations of system statecan be appointed asandrespectively. So states vector X can be written as:

1.2 Measurement equation

To observe each state directly, measurement equation is constructed by deriving the formula of observation information from inertial components and each system state. The details are as follows:

Based on the velocity error equation of SINS,Ignoring the cross-coupling of velocities (VEand VN),the projections of accelerometer outputs on the north and east axis of the navigation coordinates (n′) accordingly can be written as:

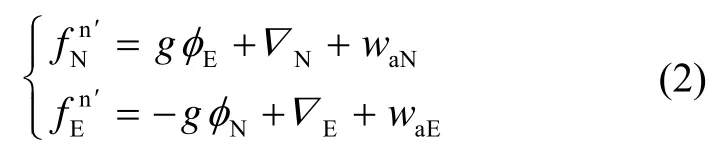
Where waEand waNare the projections of random noises of accelerometers on the East and the North axis of the navigation coordinates.

According to equations (2) and (3), the estimations of system state can be written as:

According to equations (4),

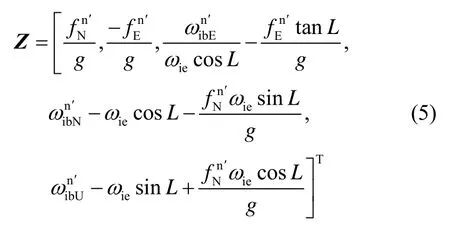
The factors of Z can be considered as the measurement of five states; therefore, the measurement equation are stated:

Where H, Gand V are as follows:

The measurements of five states directly adopt the output information of inertial components, which include high-frequency noises and will affect the initial alignment precision. Thus, the filtering pretreatment needs to be done before the application.

1.3 Kalman filter with noise-related

According to equations (1) and (6), the state noise and the observation noise are related. As a result, the Kalman filter with noise-related is applied and the equations are as follows[11]:

2 Observability and precision analysis

For the linear and invariant system by equation (1)and (6), the observability matrix of the system can be written as:

Under the condition of stationary base and based on the order-reduced model constructed, the rank of the matrix Q is 5 when the simulation latitude is 30.58 degree. Resulting from the analysis of the rank, the states of the alignment model are all observable. The singular decomposition of the matrix above is made, i.e.

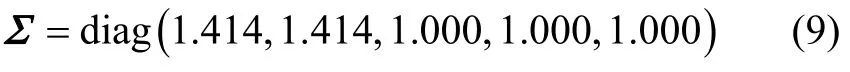
The corresponding singular value of each system states is in the same order of magnitude. As a result, all the system states are observable and the observabilities are very good.

The error analyses of the estimated states are as follows:

According to equations (4),

Equations (10) show that the five system states can be directly estimated by measurements. It’s known that in the conventional alignment method considering velocity as measurements,Eφ,Nφ andNε are estimated by measurements and their first order differential, whileUφ additional needs measurements’ differentials of second order andUε needs differentials of second and third order. In the alignment method considering velocities and gyros outputs information as measurements, the five system states are estimated by the measurements and first order differential[6]. Therefore, the alignment method of state estimation velocity in this paper is faster.

According to equations (10) and (11), the estimating errors ofEφ,Nφ,Uφ,Nεand Uε are as follows:

Equation (12) shows that the theoretical limits of accuracy of three methods are the same.

3 Application test and analyses

The application test adopts an IMU with fiber optic gyroscopes of medium accuracy, which is putted on a high precision double-axis rate turntable. The attitude reference is provided by the gradienter and the optical theodolite. The heading is 36.7°; the horizontal attitudes are basically 0°; the local longitude and latitude are 114.802°E，30.58°N respectively. The data sampling frequency of inertial components is 100 Hz. Firstly, the coarse alignment has been applied by using analytical methods. Then, the alignment method based on velocities(method 1), the one based on velocities and gyro outputs(method 2), and the new method (method 3) based on order-reduced filter have been used to do off-line precision alignments with the same set of data. The filtering frequency is 10 Hz and the alignment time is 500 s. The initial values of the filter are all set to 0 and the noise matrix is set by corresponding value of the middling precision system. Before initial alignments, a digital low-pass Butterworth filter is used to pre-process the original information of inertial components[12]. The parameters of Butterworth filter is set as follows:sampling frequency is 100 Hz; band-pass cut-off frequency is 5 Hz; band-stop cut-off frequency is 6 Hz; band-pass fluctuation coefficient is 2 dB; band-stop attenuation coefficient is 30 dB. The experimental results of estimation errors ofare shown in Figure 1, while the experimental results of estimations ofare given in Figure 2.

Fig.1 Estimation errors of Eφ,NφandUφ

According to Figure 1, the alignment precisions of three methods are relatively equivalent. The convergence rate of the horizontal misalignments with method that proposed here is the fastest since the horizontal misalignments are directly estimated by the measurements while the other two methods estimate by measurements and measurements’ differentials, reducing the convergence time from 55 s to 5 s. And the convergence rates of the azimuth misalignment between the method prompted by this article and the one based on measurements of velocities and gyros’ outputs are equivalent because the east gyro’s output play decisive role of the convergence rates, even though the azimuth misalignment is observed by outputs of east gyro and accelerator in the former method and by east gyro’s output and its first-order differential in the latter method. The convergence rate using the method based on velocities only is slowest because it needs second-order differrentials of measurements.

Fig.2 Estimations of Nε andUε

From Figure 2, the convergence rates of equivalent constant drift of north and azimuth gyros in method 2 and 3 are equivalent, resulting from the fact that the determinant is the outputs of north and azimuth gyros.Moreover, the equivalent constant drift of north gyro in the conventional method is related to the second-order differentials of the observations while equivalent constant drift of azimuth gyro is correlated to the third differentials; thus, the convergence rate of north gyro drift are extremely slow and there has been no obvious converge of azimuth gyro drift during the whole experiment. Therefore, the convergence rate of the new method is the fastest.

卓世清《题徐仙亭》上阕全篇写景：远看，一湾流水向西去。夜晚，“我”独自静坐在徐仙亭上。看不到世外高人驾鹤归去，只看到清风摇弄着翠竹的影子。下阕首句，词人深发议论。结句处则又拉回至写景，莹莹白雪，十里梅花，孤月遥挂，冷冷清清。下阕的“冷”与上阕的“静”相呼应之下，一股凛冽清昶之感由内而发。

To explain the impact of the noise from the original information of inertial components on the filtering and the efficiency of filtering, the alignments in two cases with filter and without filter for original information have been verified and the results are shown in Figure 3.

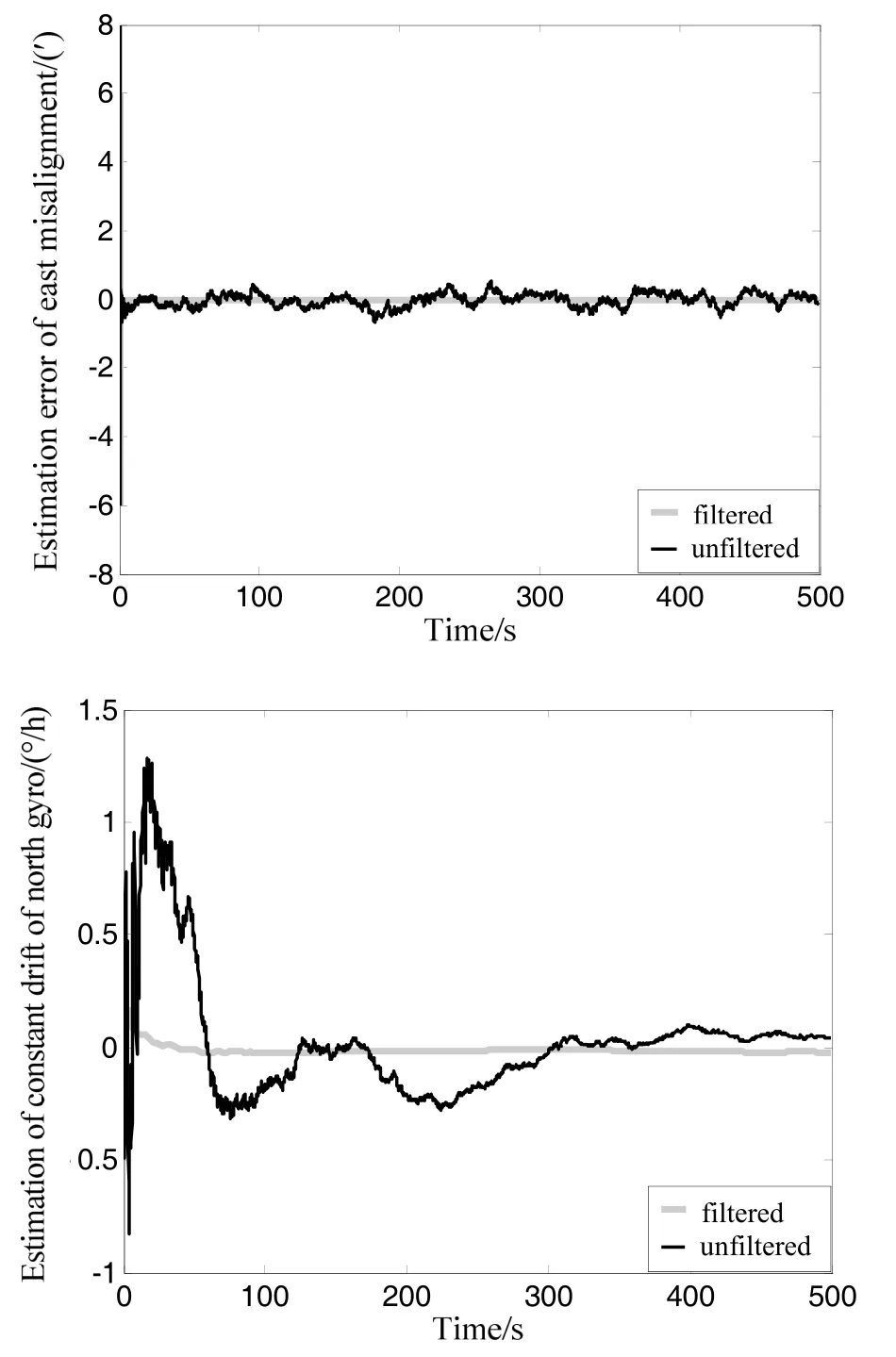
Fig.3 Estimation errors of EφandNεin two situations

According to Figure 3, the high-frequency noise in the original information has substantially affected the precision of the filtering and a low-pass filtering for the original information can effectively depress the impact of noise on alignment results.

Apart from that, the calculation of filtering is in proportion to(nis the system order andmis the number of measurements). The comparisons of the amount of calculations of three methods are in Table 1.

From Table 1, the amount of calculations with orderreduced filter is 20.83% of that in the first method and 16.67% of that in the second method, which indicates that the amount of calculations has dropped significantly.

Tab.1 Calculation comparison of three algorithms

4 Conclusion

This article has introduced an initial alignment method for SINS based on order-reduced filter and made the following conclusions by analyses and experiment verifications: first, the filtering precision in the new method and in the method with velocities and gyros outputs are relatively equivalent; second, the new method has reduced the amount of calculation significantly and improved the instantaneity of the alignment; and in the end, adopting a low-pass filter to process the original information of inertial components can efficiently depress the impact of the noise on alignment results.

[1]Zhang C B, Tian W F, Jin Z H. A novel method improving the alignment accuracy of a strapdown inertial navigation system on a stationary base[J]. Measurement Science and Technology, 2004, 15: 765-769.

[2]He Hong-yang, Xu Jiang-ning, Li Jing-shu, et al. improved fast backtracking alignment approach for stapdown inertial navigation system[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 179-183.

[3]Silson P G. Coarse alignment of a ship’s stapdown inertial attitude reference system using velocity loci[J]. IEEE Transaction on Instrument and Measurement, 2011, 60:1930-1941.

[5]Li J, Xu J, Chang L, et al. An improved optimal method for inertial alignment[J]. Navigation, 2014, 67: 727-736.

[6]高伟熙, 缪玲娟, 倪茂林. 一种引入陀螺角速度信息的快速对准方法[J]. 宇航学报, 2010, 31(6): 1596-1601.Gao Wei-xi, Miu Ling-juan, Ni Mao-lin. A fast initial alignment method with gyro angular rate information[J].Journal of Astronautics, 2010, 31(6): 1596-1601.

[7]Arunasish A, Smita S, Ghoshal T K. Improved self-alignment scheme for SINS using augmented measurement[J].Aerospace Science and Technology, 2011, 15: 125-128.

[8]Li Wan-li, Wu Wen-qi, Wang Jin-ling, et al. A fast SINS inertial alignment scheme for underwater vehicle applications[J]. The Journal of Navigation, 2013, 66: 181-198.

[9]Ali J, Mirza M R. Inertial orientation of inertial navigation system realized through modeling and filtering[J].Measurement, 2011, 44: 793-801.

[10]郭晓松, 王解, 周召发, 等. 基于观测量扩展的捷联惯导快速初始对准方法[J]. 系统工程与电子技术, 2014,36(7): 1392-137.Guo Xiao-song, Wang Jie, Zhou Zhao-fa, et al. Measurement augmentation based fast inertial alignment of SINS[J]. Systems Engineering and Electronics, 2014, 36(7):1392-137.

[11]Narasimhappa M, Sabat S J, Nayak J. Fiber-optic gyroscope signal denoising using an adaptive robust Kalman filter[J]. IEEE Sensors Journal, 2016, 16(10): 3711-3718.

[12]衣昌明, 付玉强. 基于小波分析的光纤陀螺信号处理[J]. 计算机与数字工程, 2012, 40(12): 40-42.Yi Chang-ming, Fu Yu-qiang. Study of fiber optical gyroscope signal processing based on wavelet analysis[J].Computer & Digital Engineering, 2012, 40(12): 40-42.

[13]Liu Xue-jun, Li Yong-tao. Fast alignment algorithm of inertial fixed frame in quasi-static environment[J]. Journal of Chinese Inertial Technology, 2014, 22(4): 459-462.

基于降维滤波器的SINS快速初始对准算法)

（王荣颖1，刘文超2，卞鸿巍1，高 薪1)

（1. 海军工程大学 导航工程系，武汉430033；2. 中国人民解放军91550部队，大连 116023）

引入惯性元件信息观测的初始对准方法能够快速提高 SINS的对准速度，但同时存在滤波计算量大、系统噪声与观测噪声相关以及观测值中的高频噪声影响滤波精度的问题。针对这些问题提出了一种捷联惯导快速初始对准降维滤波器设计方法，通过剔除不可观测量和合理选取状态量以降低状态方程维数，并推导了观测方程，在采用低通滤波器对惯性器件原始信息预处理基础上应用噪声相关下的 Kalman滤波进行状态估计。理论分析和试验结果表明，新方法提高了对准速度，减少了计算量，水平姿态角收敛速度提高了90%，计算量减少了83.33%，并可有效抑制高频噪声对状态估计的影响。

捷联惯导；初始对准；降维滤波器；低通滤波器；可观测性

U666.1

A

1005-6734(2016)05-0607-06

10.13695/j.cnki.12-1222/o3.2016.05.009

2016-06-08；

2016-08-06

国家自然科学基金资助项目（41406212，41201478）

王荣颖（1981—），男，讲师，主要从事惯性导航技术、组合导航技术研究。E-mail: wry441@163.com

联 系 人：卞鸿巍（1972—），男，教授，主要从事惯性导航技术、组合导航技术研究。E-mail: travisbian@foxmail.com