一种改进的模极大值混沌信号降噪方法
2016-12-22刘云侠刘培超初振云王克生
刘云侠,刘培超,初振云,王克生
(山东科技大学 工程实训中心,山东 青岛 266590)
一种改进的模极大值混沌信号降噪方法
刘云侠,刘培超,初振云,王克生
(山东科技大学 工程实训中心,山东 青岛 266590)
基于混沌和噪声的不同表现特征,提出一种改进的小波模极大值信号降噪方法。首先,该方法根据不同尺度噪声残余率的差别,确定离散二进制小波变换的最优分解尺度。然后,结合奇异谱理论对小波变换后的近似系数进行处理,去除表征噪声的较小奇异值;利用空间尺度相关性分析细节系数,自适应选取模极大值的阈值范围,提取有用信号,体现混沌系统内部特性。以Lorenz模型和月太阳黑子为例进行仿真分析,验证了本方法的可行性和实用性,提高了系统的信噪比,降低了系统的重构误差。
小波模极大值;奇异谱分析;空间尺度相关;降噪
混沌来源于确定性动力系统,具有初始敏感性和不可预测性,在各类学科中得到了广泛应用[1-2]。实际观测混沌信号都含有一定的噪声,噪声的普遍存在破坏了系统内在特性,影响了对系统的进一步研究[3],因此对混沌信号进行有效降噪具有重要意义。
近年来,小波理论的日益完善,使其在信号降噪领域发挥了重要作用[4]。在小波降噪方法中,模极大值降噪方法具备良好的理论基础,无需事先知道噪声的方差,因此能够准确刻画信号的奇异性和局部特性。模极大值方法[5-7]由Mallat等提出,能够去除噪声对应的模极大值点,对混沌信号进行有效的时频分析。关于该降噪理论的研究,也出现了一些改进方法[8-11],有基于模极大值小波域的包络降噪方法、阈值与模极大值跟踪相结合的降噪方法以及基于模极大值曲线长度阈值的降噪方法等,这些方法均具有一定降噪效果,但是在降噪过程中,小波分解尺度和模极大值阈值的准确选取较困难。
本文针对小波模极大值降噪过程中存在的问题,提出一种改进的模极大值混沌信号降噪方法。该方法首先对混沌信号进行离散二进制小波变换,然后分别利用奇异谱和尺度相关性,对近似系数和细节系数进行处理,客观确定模极大值的阈值范围,进而去除代表噪声的奇异点。为了反映降噪效果,分别从时间域和空间域对降噪前后的信号进行分析,不同角度呈现所提方法降噪的可行性。
1 基本模极大值降噪原理
信号经小波变换后,其系数的模极大值包含信号的奇异性,通过阈值的设置、分析和抑制可以实现奇异性强度的改变,达到降噪的目的[5]。
假设在L2(R)空间内,对实际观测混沌信号f(n)进行离散小波变换,可以得到:
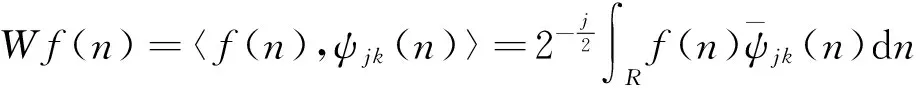
(1)
通常,信号奇异点包含本质信息,奇异性用Lipschitz指数描述。有用信号的Lipschitz指数为正值,噪声的Lipschitz指数为负值。小波变换的模极大值与Lipschitz指数之间具有如下的关系:

(2)
其中:系数A>0,b表示离散小波平移因子的系数。有用信号和噪声在小波不同分解尺度上的模极大值具有不同的特性。α>0时,小波模极大值随着分解尺度的增大而增大,说明该处的奇异性主要由信号引起;反之,模极大值随着尺度的增大而减小,说明该处的奇异性主要由噪声引起。
基本的小波模极大值降噪方法具有一定的实用性,但是分解尺度和模极大值阈值范围的确定比较困难。小波变换分解尺度过多过少,都会导致有用信号丢失,信噪比下降。模极大值范围选取不当,也会造成各个尺度上对应的小波系数中含有的噪声较多,降噪偏差增大。
2 一种改进模极大值降噪方法
针对基本模极大值降噪方法的缺点,本文提出一种改进的模极大值降噪方法。该方法先对混沌信号进行离散二进制小波分解,噪声包含在由高频组成的细节系数中。通过细化小波分解信号,利用噪声残余率的计算确定最优的分解尺度,结合尺度相关性分析自适应确定模极大值的阈值范围,来对小波系数进行处理,实质是抑制信号中的噪声恢复有用信号。
改进的模极大值降噪方法的基本过程如下:
1)选取合适的离散二进制小波,对含噪声混沌信号进行J尺度小波分解,确定最优的分解尺度。本文主要通过小波变换后不同尺度上小波系数的噪声残余率来确定最优分解尺度,从而解决基本模极大值降噪方法分解尺度难确定的问题。
2)小波分解近似系数分析。虽然近似系数是有用信号的近似,但仍包含一定的噪声成分,本文主要对其进行奇异谱分解,去除较小代表噪声的奇异值。
3)小波分解高频细节系数模极大值阈值范围的客观自适应选取。结合空间尺度相关分析对模极大值的阈值进行量化处理,保留系数中的有用信息,从而解决基本模极大值降噪方法模极大值阈值范围难确定的问题。
4)为了对本文提出降噪方法的降噪效果进行验证,主要从时间域和空间域进行分析,多角度体现降噪的性能。
在以上过程中,关键的是最优分解尺度和模极大值阈值范围的确定。从某种程度上讲,模极大值阈值范围的准确选取直接关系着降噪的效果和对信号的进一步分析。
2.1 最优分解尺度选取
利用离散二进制小波对信号进行变换,分解尺度的选取非常重要。最优分解尺度的确定,利于小波系数的准确分析,提高系统的信噪比。通过小波变换后不同尺度上小波系数的噪声残余率来确定最优分解尺度,噪声残余率的定义为:

(3)
通过式(3)可以看出,当噪声残余率取值最小时,所对应分解尺度的近似系数越逼近原始有用信号,即为小波变换的最优分解尺度。
2.2 小波分解近似系数分析
混沌信号经过小波变换,会被分解为近似系数和细节系数。基本模极大值降噪方法只对细节系数进行分析,忽略了近似系数中的噪声,降噪效果不明显。在充分考虑混沌和噪声特性的基础上,对近似系数和细节系数分别进行分析。


(4)


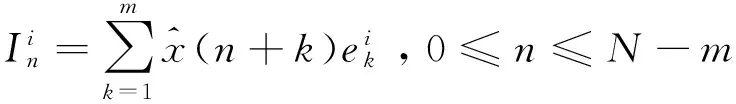
(5)
选取前l个主分量和特征向量对近似系数进行重构,可以得到:

(6)
重构后的近似系数,进一步降低了信号中的噪声,能够增强系统的整体特性。
2.3 细节系数模极大值分析
模极大值阈值范围的选取与降噪的效果有着直接关系,也是信号降噪的关键。为了客观准确地对模极大值阈值范围自适应选取,本文采用空间尺度相关性对细节系数进行分析。由于有用信号和噪声能量随着尺度的增大变化不同,因此可以对不同尺度细节系数进行相关性分析。
假设信号小波变换后尺度j上位置n处的细节系数为dj(n),那么相关系数矩阵如式(7)所示:
Cj(n)=dj(n)×dj+1(n)。
(7)
由于相邻尺度信号相互影响,一般选取相关运算的尺度数为2。同时,定义归一化相关系数矩阵如下:

(8)

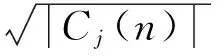
(9)
对细节信号dJ(n),有用信号的能量较大,噪声的能量较小,因此模极大值的阈值范围选取不应太大,以免去除过多的有用信号。此时,可以通过比较NorCj(n)与dj(n)的绝对值对细节系数进行分析,具体如下:

(10)
对经过上述处理的近似系数和各层细节系数进行重构,就得到了降噪后的信号,即:

(11)
通过分析可以看出,该降噪方法能够更大程度的保留信号,去除噪声,体现系统的结构特性。
2.4 降噪评价标准
为验证所提方法降噪效果的优劣,主要从以下两个方面分析。
一方面,对已知动态特性的混沌信号,计算其信噪比SNR和均方根误差RMSE,公式分别如下:
(12)
另一方面,对实际观测混沌信号,从时间相关性Tcorr及空间递归性Rec分析,公式分别如下:
(13)

对于混沌信号,具有低频特性,自相关函数值远大于噪声,递归图对称且具有一定的规律性,确定性和递归度较大。相反,噪声具有高频特性,自相关函数值较小,递归图杂乱无章。因此,可以通过以上指标对降噪前后的信号进行分析,从而反映降噪方法的性能。
3 仿真实例分析
基于以上理论,本文主要对加噪声的Lorenz混沌信号和实际观测太阳黑子进行降噪分析。
3.1 Lorenz系统
Lorenz为已知动态特性的系统,其模型方程如下:

(14)
当σ=10,r=28,b=8/3时,Lorenz为混沌系统。利用离散二进制小波db2~db10分别对加噪20%的Lorenz混沌信号进行6尺度小波变换,各个尺度小波系数的噪声残余率如表1所示。
由表1可以看出,噪声残余率随着分解尺度的增加先减小后增大,这主要是由于信号中包含噪声所致。当分解尺度为3时,小波系数的噪声残余率最小。因此,采用本文方法对混沌信号降噪时,选择db7小波,最优分解尺度为3。
表1 不同尺度的噪声残余率
Tab.1 Noise residual rate in different scales

分解尺度噪声残余率db2db3db4db5db6db7db8db9db1010.52180.52660.52260.51400.50680.50540.50980.51610.519620.28580.26910.25730.27470.27660.26020.26950.27980.264430.18280.15260.14130.14410.14090.14060.14120.13910.142940.62890.38160.25460.30780.21790.19790.24640.17500.183953.06882.62502.61152.41652.25002.19342.25612.23492.039368.93688.88509.38299.33099.02659.32599.51289.32359.3740
分别利用基本的小波模极大值方法、小波阈值方法和本文方法对加噪20%的Lorenz信号降噪,降噪前后的相空间图如图 1所示:

图1 Lorenz信号降噪相空间比较
Fig.1 Phase space comparision of Lorenz signal before and after noise reduction
当噪声水平分别为5%、10%、15%、20%、30%、 50%、70%、90% 和100%时,降噪后系统SNR和RMSE 曲线如图2所示。

图2 不同噪声水平下的SNR和RMSE曲线
Fig.2 SNR and RMSE Curves under different noise levels
通过对比可以看出,本文方法能够对已知动态特性的Lorenz混沌信号进行有效的降噪,在提高信噪比的同时,降低了系统的均方根误差。
3.2 太阳黑子
太阳黑子,能够反映太阳的活动,对地球水文、气候的变化有着直接影响[12]。由于环境、噪声各种因素的影响,实际观测太阳黑子数的混沌特性不明显,影响进一步的研究,因此对其进行有效的降噪具有很重要的意义。
选取1761年1月到2010年12月共3 000个太阳黑子数,利用db7小波进行3尺度离散二进制小波变换,分别采用基本模极大值方法、小波阈值方法和本文方法对其进行降噪。在时间域,降噪前后太阳黑子及本文方法降噪后去除噪声部分的自相关函数值如表2所示。
在空间域,主要是对实际观测太阳黑子进行递归分析。递归现象是确定性动力系统的一个最基本的特征,也是混沌系统的特点。取降噪前后200个数据,当嵌入维数为5,延迟时间为1,空间信号距离为10时,进行仿真分析,三种方法降噪前后的递归图如图3所示。

表2 自相关函数值

图3 太阳黑子递归图
Fig.3 Recursive graphs of sunspots
通过表2和图3可以看出,采用本文方法降噪后的太阳黑子自相关性更强,远大于去除噪声部分的自相关函数值,实际观测太阳黑子的递归规律杂乱无章,采用降噪方法降噪后,呈现了一定的递归和确定性。通过对比发现,本文方法在去除系统噪声的同时,很好的展现了系统的混沌动态特性,从而为进一步的研究提供了理论基础。
4 结论
本文根据信号和噪声在小波变换不同尺度上有不同的表现特性,结合奇异谱和空间尺度相关分析,对基本模极大值降噪方法进行了改进。改进降噪方法不仅能够对实际观测混沌信号进行有效降噪,而且降噪性能稳定,能够很好保持信号的奇异性和光滑性。通过对Lorenz和实际观测太阳黑子进行仿真试验,并从信噪比、均方根误差、自相关函数及递归图等方面对降噪效果进行对比,证明了本文改进方法降噪的有效性。
[1]MOLAIE M,JAFARI S,MORADI M H,et al.A chaotic viewpoint on noise reduction from respiratorysounds[J].Biomedical Signal Processing and Control,2014,10:245-249.
[2]WU Q,LAW R,WU E,et al.A hybrid-forecasting model reducing Gaussian noise based on the Gaussian support vector regression machine and chaoticparticle swarm optimization[J].Information Sciences,2013,238(20):96-110.
[3]BEHERA S K,DAS D P,SUBUDHI B.Functional link artificial neural network applied to active noise control of a mixture of tonal and chaotic noise[J].Applied Soft Computing,2014,23:51-60.
[4]MURGUIA J S,CAMPOS C E.Wavelet analysis of chaotic time series[J].Revista Mexicana De Fisica,2006,52(2):155-162.
[5]MALLAT S,WEN L H.Singularity detection and processing with waveletes[J].IEEE Transactions on Information Theory,1992,38(2):617-643.
[6]ZHANG L,BAO P,PAN Q.Threshold analysis in wavelet-based denoising[J].Electronics Letters,2001,37(24):1485-1486.
[7]DAVID L,DONOHO J.Denoising by soft-thresholding[J].IEEE Transactions on Information Theory,1995,41(3):613-627.
[8]HSU C F.Adaptive fuzzy wavelet neural controller design for chaos synchronization[J].Expert Systems with Applications,2011,38(8):10475-10483.
[10]HAN M,LIU Y,XI J.Noise smoothing for nonlinear time series using wavelet soft threshold[J].IEEE Signal Processing Letters,2006,14(1):62-65.
[12]GEORGE L,XENOPHON M.The sunspot as an autonomous dynamical system:A model for the growth and decay phases of sunspots[J].Physica A:Statistical Mechanics and Its Applications,2007,379(2):436-458.
(责任编辑:傅 游)
An Improved Modulus Maximum Method for Noise Reduction of Chaotic Signals
LIU Yunxia,LIU Peichao,CHU Zhenyun,WANG Kesheng
(Engineering Training Center,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)
Based on the different features between chaos and noise,an improved wavelet modulus maximum method is proposed for noise reduction of signals. Firstly,the optimal decomposition yardstick of discrete binary wavelet is determined by noise residual rate analysis in different scales. Secondly,the approximate coefficients are handled by the singular spectrum analysis in order to remove the less singular value which can character noise,while the spatial scales relevancy is used for the analysis of the wavelet coefficients in different scales in order to determine the threshold range of the wavelet modulus maximum treatment adaptively and reserve the useful signals mixed in noise and reflect the internal characteristics of chaotic system. The chaotic signals generated by Lorenz model and monthly sunspots are respectively applied for simulation analysis,the numerical experiment results confirm the advantages of the method raised in this paper,including the improved signal to noise ratio and the reduced reconstruction error of the system.
wavelet modulus maximum; singular spectrum analysis; spatial scales relevant; noise reduction
2016-01-14
刘云侠(1983—),女,山东临沂人,助教,硕士,主要从事非线性信号处理和智能控制的研究. E-mail:liuyunxia06@163.com
TN911
1672-3767(2016)05-0114-07
