海上漂浮式风力机Spar平台波频与慢漂响应性能分析

王东华，叶 舟,2，郝文星，张 楠，李 春,2

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)



海上漂浮式风力机Spar平台波频与慢漂响应性能分析

王东华1，叶 舟1,2，郝文星1，张 楠1，李 春1,2

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

建立OC3-Hywind Spar Buoy平台的NREL 5 MW漂浮式风力机整机模型，采用基于辐射绕射理论的面元法和完整的二阶传递函数(QTF)计算一阶与二阶波浪载荷，并利用叶素-动量理论对叶片气动载荷进行计算.对一阶与二阶波浪载荷以及由其引起的波频与慢漂响应进行对比分析，并分别讨论风、浪联合作用和不同海况下风、浪、流联合作用时的波频与慢漂响应.结果表明：一阶波浪载荷比二阶波浪载荷至少大1个量级，但两者引起的动态响应幅值在同一个量级；气动载荷不仅影响慢漂响应，而且对波频响应也有一定影响；波频响应主要受海浪影响，慢漂响应主要受气动载荷影响.

漂浮式风力机； 波频响应； 慢漂响应； Spar； QTF

风能是一种十分清洁的可再生能源，随着风能资源的不断开发，未来风电场建设的必然趋势是“由陆向海、由浅向深、由固定式基础结构向漂浮式平台”[1-2].

漂浮式风力机是一个涉及空气动力、水动力、弹性体和控制等多方面模型的复杂系统，对其进行整体动态响应分析必须考虑各部分之间的耦合作用.其复杂的动力学特性和特有的技术难题一直是国内外学者研究的热点.Spar平台的动态响应可分为波频响应和慢漂响应，波频响应属于一阶响应，慢漂响应属于二阶响应.目前，波频响应已有了成熟的理论和计算方法，慢漂响应是二阶低频力、风力与海流力相互耦合后与Spar平台作用的现象，逐渐成为研究的热点.王世圣等[3]在南海TLP石油平台概念设计中采用Newman近似方法得到了二阶波浪载荷，并给出了平台在风、浪、流作用下的动态响应.然而Pinkster等[4-5]的研究发现，Newman近似法得到的二阶波浪载荷与实际值相差约20%.Goupee等[6-7]通过模型实验验证了二阶波浪载荷对漂浮式风力机平台的影响不容忽视.国际上对漂浮式风力机进行分析的软件(如ADAMS、GH Bladed、3Dfloat和SIMPACK)均未考虑二阶或高阶波浪载荷[8].Roald等[9]采用WAMIT和FAST结合的方法在频域计算了二阶波浪载荷对漂浮式风力机平台动态响应的影响.频域分析只能分析简单的线性问题，而时域分析能够较好地处理复杂受力系统的动态响应问题.FAST在8.10版本以后也开始关注二阶波浪载荷对漂浮式风力机平台的影响，但目前其尚不能单独计算载荷对波频响应与慢漂响应的影响[10].可见，目前关于Spar平台漂浮式风力机的研究，特别是关于波频响应与慢漂响应的研究还较少.

为探究风、浪、流载荷对波频响应与慢漂响应的影响，笔者建立了Spar平台漂浮式风力机整机模型，采用叶素-动量理论计算气动载荷，采用AQWA计算一阶、二阶波浪载荷与流载荷，通过动态链接库(DLL)把气动载荷和水动力载荷耦合在一起，在时域范围内分别分析了波浪载荷、风载荷及不同海况对漂浮式风力机波频响应与慢漂响应的影响，为漂浮式风力机的安全运行提供参考.

1 漂浮式风力机模型

基于OC3-Hywind Spar平台的漂浮式风力机由Spar平台主体和风力机2部分组成，Spar平台主体为一深吃水的细长浮筒，3根悬链线成120°张开，且在一定预张力作用下处于半张紧半松弛状态.Spar平台和美国国家能源部可再生能源实验室(NREL) 5 MW风力机主要参数参考文献[11].基于NREL 5 MW风力机参数和Spar平台参数建立漂浮式风力机整机模型，如图1所示.

图1 OC3-Hywind Spar漂浮式风力机整机模型Fig.1 Model of a offshore floating wind turbine based on OC3-Hywind Spar platform

2 理论基础

2.1 波浪载荷[12]

海上漂浮式风力机的环境载荷比陆上风力机更加复杂，除风载荷的影响外，还会受到波浪载荷的作用，这是海上漂浮式风力机与陆上风力机的最大不同之处.随机波浪可以视为无数振幅不同、频率不同、初始相位随机的余弦函数的叠加，作用在平台的波浪载荷可以通过辐射绕射理论求得.假设流体是无黏、无旋、均质不可压缩的势流，在这些假设下，可以用速度势函数描述平台周围的环绕流体，并且该速度势Φ在流体各处应满足拉普拉斯方程和物体表面、自由表面、海底及无穷远处的边界条件.

速度势Φ的摄动展开式为

Φ=εΦ(1)+ε2Φ(2)+…

(1)

式中：ε为小量；Φ(1)和Φ(2)分别代表一阶速度势和二阶速度势，二者同时满足海底、自由表面、物体表面及无穷远处的边界条件.

沿坐标轴正向传播的长峰不规则波的波面ζ的方程可以表示为

(2)

式中：Aj为波幅，m；ωj为波频率，rad/s；kj为波数，m-1；εj为随机相位；x为沿坐标轴方向的位移，m；j为规则波的个数；t为时间，s.

一阶波浪载荷的计算是将自由表面线性化处理，得到一阶波浪传递函数.

(3)

(4)

其中，

(5)

式(5)中第1项为水线上的积分，第2项为伯努利方程，第3项为加速度，第4项为动量，第5项为二阶波浪势.Newman近似法通过计算i=j部分的漂移力来近似估算二阶力.

2.2 海流载荷

海流是洋流、潮流和风共同作用下表面水团驱动效应的叠加.洋流的周期约为几个月，根据海域的不同，潮流有一昼夜或半昼夜周期.可以认为在某一给定海况下，海流在速度和方向上不随时间变化，而其速度会在不同水深中发生变化.工程上常假定海流速度沿着水深方向呈线性变化或二次曲线变化，海底海流速度几乎为零，浅水域流速通常处理为二次曲线变化，深水域流速通常处理为线性变化.本文Spar平台漂浮式风力机设计水深320 m，属于深水作业环境，故海流载荷Fcurrent简化为线性变化[13]：

(6)

式中：S为结构物受力部分等效面积，m2；Uc为海流的速度，m/s；CD为阻力系数，取0.7.

2.3 气动载荷

与陆上风能相比，海上风能具有平均风速高、湍流度低、风剪切小等特点.风力机高耸的上部结构受风面积大，风能对其影响非常重要.风力机风轮气动力计算方法主要分为叶素-动量理论(BEMT)方法、二维势流方法和计算流体力学(CFD)方法3大类，其中二维势流方法又分为加速度势方法和涡尾迹方法2类.叶素-动量理论方法简单有效，故本文中风轮气动力的计算采用叶素-动量理论方法[14].

正常运行状态下，旋转的风轮扫略面积很大(相当于直径126 m的圆盘)，塔架的投影面积很小(90 m×6 m)，作用在风轮上的气动载荷如图2所示，约为780 kN，而此时作用在塔架上的气动载荷仅为30 kN，可以忽略.风力机正常运行时，风轮所受气动载荷F1如下：

(7)

式中：CT为轴向推力系数，取0.78；ρa为空气密度，kg/m3；A1为风轮的扫略面积，m2；Vh(t)为海平面10 m高度处的相对风速，m/s.

来流风速未达到切入风速或超过切出风速时，风轮处于停转状态，风轮承受气动载荷的方式发生改变，风轮受到的气动载荷和塔架受到的气动载荷基本相等，不能忽略，风力机上部所受气动载荷为

(8)

式中：A2为塔架和风轮叶片在来流风方向的正投影面积，m2.

图2 风轮的气动载荷Fig.2 Aerodynamic load on the wind turbine rotor

2.4 运动方程

根据傅里叶变换和卷积积分的方法，时域下Spar平台的运动方程[15]为

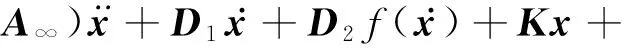
(9)

h(τ)为迟延函数，可通过与频率相关的附加质量C(ω)和附加阻尼变换得到，即

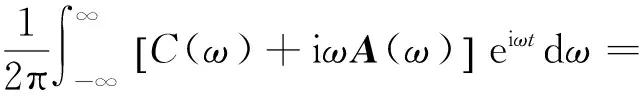
(10)

其中，H(ω)=C(ω)+iωA(ω).

波频响应可以在频域内求解，其为波浪的线性响应，这就意味着二阶阻尼矩阵D2为零，同时回复力刚度矩阵K恒定.频域内波频响应可以表示为

(11)

慢漂响应可以通过时域内的动态平衡方程求解

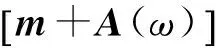
(12)

式中：下标HF和LF分别代表波频响应和慢漂响应.

3 载荷条件和计算模型

波浪谱是随机海浪的一个重要统计性质，它直接给出海浪组成波能量相对于频率的分布.常用的波浪谱形式有Pierson-Moskoweitz谱(P-M谱)、JONSWAP谱、Neumaim谱(劳曼谱)和Bretschnei-der谱(布氏谱).P-M谱是皮尔逊等人根据大量的实测数据于1964年提出的波浪谱，其适用于描述充分成长的波浪.P-M谱是经验谱，依据的资料比较充分，分析方法合理、使用方便，故选择P-M谱：

(13)

式中：S(ω)为波浪谱密度,m2·s；ω为波浪圆频率，rad/s；Hs为有义波高，m；Tz为跨零周期，s.

一种海况的持续时间通常是3 h，本文中选取3种北大西洋实测海况，模拟时长选取3 h，步长设为1 s，排除初始时刻的干扰后，取4 000～6 000 s来分析平台波频响应与慢漂响应.环境条件设定如表1所示.

漂浮式风力机在外界载荷作用下可视为具有6个自由度的刚体，6个自由度上的运动包括沿x轴、y轴和z轴的平动及绕各轴的转动.平动包括纵荡、横荡和垂荡，其大小用长度单位表示；转动包括横摇、纵摇和艏摇，其强弱用角度单位表示.平台在6自由度上的运动如图3所示.

表1 环境条件Tab.1 Environmental conditions

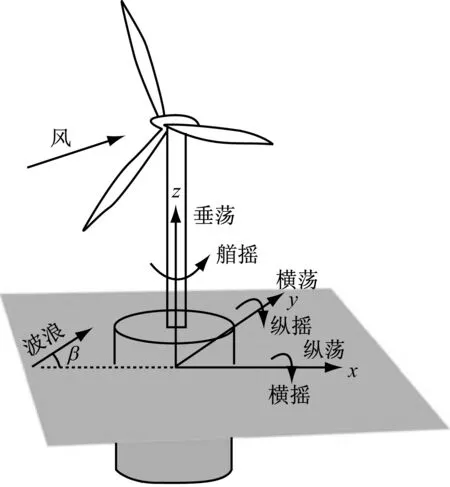
图3 6个自由度示意图Fig.3 Six degrees of freedom

假定风、浪、流垂直入射风力机风轮迎风面方向的最恶劣海况即x轴方向，同时考虑对称性，故只需分析纵荡、垂荡和纵摇方向的波频响应与慢漂响应特性.

4 结果与分析

4.1 运动响应算子RAO

图4为Spar平台3个自由度的运动响应算子随频率的变化情况，横坐标表示波浪圆频率，纵坐标表示对应单位波幅的位移与偏转角.纵荡方向，RAO随频率的增大逐渐减小，最大值为1.8；垂荡方向，RAO随频率的增大呈现先增大后减小的趋势，在0.2 rad/s左右达到最大值5;纵摇与垂荡相互耦合，变化趋势相同，最大值为2.3个自由度下，低频时响应幅度很大，且模拟值与文献[16]的实验值相符，证明模拟结果具有较高的真实度和可信度.

(c) 纵摇

4.2 波浪载荷作用下响应分析

为探究一阶波浪载荷与二阶波浪载荷及其引起的波频响应与慢漂响应对漂浮式风力机的影响，本节仅考虑波浪载荷对Spar平台的影响.工况2接近正常工况，为本节的计算工况.图5为不同自由度下波浪载荷(力矩)随时间变化的对比.纵荡方向，一阶波浪载荷与二阶波浪载荷的波动范围分别为-1 000～1 000 kN、-40～40 kN,前者比后者大1个数量级.垂荡方向，一阶波浪载荷的变化范围为-400～400 kN，而二阶波浪载荷仅在0～8 kN内波动，前者比后者大2个数量级.纵摇方向，一阶波浪力矩和二阶波浪力矩波动的峰值分别为7.5×104kN·m和4×103kN·m.由此可知，纵荡和纵摇方向，一阶波浪载荷(力矩)比二阶波浪载荷(力矩)大1个数量级；垂荡方向前者比后者大2个数量级，且二阶波浪载荷的方向沿z轴正向.

图5 波浪载荷(力矩)对比Fig.5 Wave force (moment of force) vs. time under different degrees of freedom

一阶波浪载荷引起波频响应，二阶波浪载荷引起慢漂响应.图6为波浪载荷作用下Spar平台动态响应的时域历程.纵荡方向，波频响应和慢漂响应的平均位置分别在0 m和0.2 m处附近，振幅均为0.1 m，前者的周期小于后者.垂荡方向，波频响应的平均位置在波面，最大值为0.15 m；慢漂响应的平均位置在重心上方2 m处，幅值为0.1 m.纵摇方向，波频响应与慢漂响应的平均位置均在0°附近，幅值分别为0.1°和0.15°.

对比一阶波浪载荷与二阶波浪载荷以及由其引起的波频响应与慢漂响应可知，一阶波浪载荷比二阶波浪载荷至少大1个数量级，两者引起的动态响应却在同一个数量级上.

4.3 风、浪载荷作用下响应分析

风力机的上部风轮运行过程中扫略面积很大，对动态响应的影响不容忽视，因此探究波浪载荷和气动载荷的联合作用对漂浮式风力机的影响具有重要的工程意义.图7为工况2下风、浪联合作用时Spar平台的动态响应.纵荡方向，波频响应与慢漂响应的平均位置分别在0 m和22.4 m处，幅值分别为0.3 m和0.6 m；垂荡方向，波频响应的平均位置在波面，慢漂响应的平均位置在重心上方1 m处附近，最大值均为0.2 m；纵摇方向，波频响应与慢漂响应的平均位置分别在0°和3°附近，最大值分别为1.9°和6°.

图6 波浪作用下波频响应与慢漂响应的对比Fig.6 Comparison of wave frequency and slow drift response under the action of waves

图7 风和浪联合作用下波频响应与慢漂响应的对比Fig.7 Response of wave frequency and slow drift under the combined action of wind and wave

与只有波浪载荷作用时对比，风、浪联合作用下的波频响应在3个自由度的波动幅值均变大，增加值依次为0.2 m、0.05 m和1.8°，平均位置均未改变.慢漂响应在3个自由度的幅值增加量依次为0.5 m、0.1 m和5.85°，平均位置变化很大，纵荡方向前进22.2 m，垂荡方向下降1 m，纵摇方向变化3°.综合可知，气动载荷不仅影响慢漂响应还影响波频响应，对慢漂响应的影响主要体现在增大幅值和改变平均位置两方面，对波频响应的影响仅体现在增大幅值上.

4.4 不同海况下动态响应分析

为更加真实地反映Spar平台动态响应，综合考虑一阶波浪载荷、二阶波浪载荷、海流力、风力及平台与系泊系统之间的耦合作用，计算3种海况下海上漂浮式风力机整体的波频响应与慢漂响应.时域结果具有随机性，根据挪威船级社(DNV)规范，改变波浪随机种子，使用多次计算求取平均值的方法得到统计结果(如表2所示).由不同海况的动态响应可知，波频响应是均值为0的往复运动，随着波浪强度的增加，响应幅值变大，工况3条件下波频响应最剧烈；慢漂响应是某位置的往复运动，主要受风轮气动载荷的影响，在工况2条件下响应最剧烈.Zambrano等[17]指出，正常发电时，漂浮式风力机系统的平均俯仰角需小于±5°，动态俯仰角小于±15°，该系统满足要求，能适应多种海况.

表2 时域统计结果Tab.2 Statistic results of time domain analysis

5 结 论

(1) 低频时，纵荡、垂荡和纵摇3个自由度方向的RAO很大，垂荡与纵摇方向的响应相互耦合，RAO的变化趋势一致.

(2) 一阶波浪载荷比二阶波浪载荷至少大1个数量级，而两者引起的动态响应幅值则是同一个数量级.

(3) 气动载荷不仅影响慢漂响应，同时也响应波频响应.

(4) 波频响应是均值为0的往复运动，随着波浪强度的增加，响应幅值变大；慢漂响应是某位置的往复运动，主要受风轮气动载荷的影响.

[1] PANTALEO A, PELLERANO A, RUGGIERO F,etal. Feasibility study of off-shore wind farms: an application to Puglia region[J]. Solar Energy, 2005, 79(3): 321-331.

[2] 丁勤卫, 李春, 周国龙, 等. 陆海风力机动态响应对比[J]. 动力工程学报, 2016, 36(1): 65-73.

DING Qinwei, LI Chun, ZHOU Guolong,etal. Comparison of dynamic response between stationary and floating wind turbines[J]. Journal of Chinese Society of Power Engineering, 2016, 36(1): 65-73.

[3] 王世圣, 谢彬, 李新仲. 在南海环境条件下深水典型TLP的运动响应分析[J]. 中国造船, 2011, 52(增刊1): 94-101.

WANG Shisheng, XIE Bin, LI Xinzhong. The motion response analysis of deep water typical TLP in environment conditions of South China Sea[J]. Shipbuilding of China, 2011, 52(S1): 94-101.

[4] PINKSTER J A. Low frequency second order wave exciting forces on floating structures[M]. Wageningen, Netherlands: Netherlands Ship Model Basin, 1980.

[5] LARSEN K, SANDVIK P C. Efficient methods for the calculation of dynamic mooring line tension EUROMS' 90[C]//The First European Offshore Mechanical Symposium. Trondheim, Norway: ISOPE, 1990.

[6] GOUPEE A J, KOO B J, KIMBALL R W,etal. Experimental comparison of three floating wind turbine concepts[C]//Proceedings of the 31st International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, Brazil: ASME, 2012.

[7] GOUPEE A J, KOO B, LAMBRAKOS K F,etal. Offshore wind energy: model tests for three floating wind turbine concepts[C]//Proceedings of the Offshore Technology Conference. Houston, Texas, USA: Offshore Technology Conference, 2012.

[8] 刘毅. 单柱式浮式风机结构强度分析方法研究[D]. 上海: 上海交通大学, 2014.

[9] ROALD L, JONKMAN J, ROBERTSON A,etal. The effect of second-order hydrodynamic on floating offshore wind turbines[J]. Energy Procedia, 2013, 35: 253-264.

[10] JONKMAN M J, BUHL M L. FAST user's guide[R].Colorado, USA: National Renewable Energy Laboratory, 2005.

[11] JONKMAN J, BUTTERFIELD S, MUSIAL W,etal. Definition of a 5 MW reference wind turbine for offshore system development[R]. Colorado,USA:National Renewable Energy Laboratory (NREL), 2009.

[12] 闫功伟. 新型深吃水多柱延伸式张力腿平台的概念设计与耦合运动响应分析[D]. 哈尔滨: 哈尔滨工业大学, 2013.

[13] 贝尔纳·莫兰. 海洋工程水动力学[M]. 刘水庚, 译. 北京: 国防工业出版社, 2012.

[14] NIELSEN F G, HANSON T D, SKAARE B. Integrated dynamic analysis of floating offshore wind turbines[C]//Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering. Hamburg, Germany: American Society of Mechanical Engineers, 2006: 671-679.

[15] LARSEN K, SANDVIK P C. Efficient methods for the calculation of dynamic mooring line tension[C]//Proceedings of the First ISOPE European Offshore Mechanics Symposium. Trondheim, Norway: ISOPE, 1990.

[16] KIM Y H, HONG S Y, NAM B W,etal. A numerical study of the motion and structural responses of interlinked spars in irregular waves[J]. Journal of Ocean and Wind Energy, 2014, 1(3): 161-169.

[17] ZAMBRANO T, MACCREADY T, KICENIUK T,etal. Dynamic modeling of deep water offshore wind turbine structures in Gulf of Mexico storm conditions[C]//Proceedings of 25th International Conference on Offshore Mechanics and Arctic Engineering. Hamburg, Germany: ASME, 2006.

Analysis on Wave Frequency and Slow Drift Response of a Spar Platform for Offshore Floating Wind Turbines

WANGDonghua1,YEZhou1,2,HAOWenxing1,ZHANGNan1,LIChun1,2

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China; 2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

A model was established for the NREL 5 MW floating wind turbine seating on an OC3-Hywind Spar Buoy platform, with which the first- and second-order wave forces were respectively calculated using the panel method based on radiation/diffraction theory and the quadratic transfer function, while the aerodynamic load of blades was determined according to the blade element momentum theory. In addition, a comparative analysis was conducted on the first- and second-order wave force and their resulting wave frequency and slow drift response respectively under the combined wind-wave effect and wind-wave-current effect. Results show that the first-order wave force is at least one order greater in magnitude than the second-order wave force, but the response amplitude caused by them is at the same level. Wind load affects not only the slow drift response but also the wave frequency response. The wave frequency response is mainly affected by waves, while the slow drift response is basically affected by wind.

offshore floating wind turbine; wave frequency response; slow drift response; Spar; QTF

2016-01-21

2016-02-17

国家自然科学基金资助项目(51176129,51676131)；教育部高等学校博士学科点专项科研基金(博导)资助项目(20123120110008)；上海市教育委员会科研创新(重点)资助项目(13ZZ120,13YZ066)；上海市研究生创新基金资助项目(JWCXSL1402)

王东华(1990-)，男，河南周口人，硕士研究生，研究方向为风力发电. 叶 舟(通信作者)，男，副研究员，电话(Tel.):15901788370;E-mail：wric123@gmail.com.

1674-7607(2016)11-0907-07

TK83

A 学科分类号：