进化计算与复杂网络结构关系的研究★

生龙，广晓芸

（河北工程大学 信息与电气工程学院，河北 邯郸 056038）

进化计算与复杂网络结构关系的研究★

生龙，广晓芸

（河北工程大学 信息与电气工程学院，河北 邯郸 056038）

基于达尔文进化论的进化算法可以将问题的求解过程模拟为群体的适者生存过程，通过群体不断进化，求得最终解。但进化过程的描述不够清晰，且只注重最终结果，常常忽略算法的中间过程。复杂网络结构可有效弥补这一缺陷。通过分析算法的优化过程，将个体之间的关系进行动力学过程描述，并讨论其蕴含的复杂网络结构，最终利用复杂网络技术控制或改进算法。设置相关参数进行动力学描述的实验设计并验证网络结构是否符合复杂网络特征。研究结果表明进化计算的优化过程可以描述为复杂网络结构或类似于复杂网络的结构。这对于复杂网络的深入研究及进化计算的改进、优化和控制有一定的理论意义和应用价值。

进化计算；复杂网络；动力学；网络结构；优化

0 引言

本文对两个看似完全不同的研究领域：进化计算和复杂网络的相互关系进行简要研究[1]。进化算法（Evolutionary Algorithms，EAs）是以达尔文的进化论思想为基础，通过模拟生物进化过程与机制的求解问题的自组织、自适应的人工智能技术，遵循优胜劣汰，适者生存的原则[2]。进化计算具有效率高、简单、易操作、鲁棒性强和通用性好等特点，能够不受问题性质的限制，有效地处理传统优化算法难以解决的复杂问题。但传统的描述形式不够清晰，直观，不利于理解，且只注重计算结果，忽视了算法的中间过程。因此分析算法的优化过程，用隐含的网络结构动力学演化过程描述优化过程并分析网络结构动力学特征将成为进化计算和复杂网络研究的一大亮点[2，3]。

复杂网络作为大量真实复杂系统的高度抽象，为研究问题的解决提供了一种新视角、新方法、新工具。通过复杂网络结构的分析可以揭示网络内部的拓扑结构，理解其功能，预测其行为。这两个看似无关的研究领域：进化计算和复杂网络，是否存在某种隐含关系将成为研究重点。如何根据优化过程中染色体的相互关系构建网络拓扑结构模型并展现进化计算中隐含的拓扑结构的动力学演化过程将成为研究的难点与关键。

目前为止关于进化计算和复杂网络动力学关系的研究文献较少。本文从进化计算的优化过程入手，重点分析进化计算和复杂网络之间的相互关系，详述算法的中间过程，并讨论进化算法的可视化步骤。希望对国内关于进化计算中复杂网络动力学的研究起到推动作用。

1 进化计算的基本概念

进化计算是计算科学的子学科，属于生物计算领域。二战结束以来，进化计算的主要思想被广泛的引入到科学界[1]。进化算法主要包括遗传算法（Genetic Algorithms，GA）[4]、遗传规划（Genetic Programming，GP）[5]、进化策略（Evolution Strategies，ES）[6]和进化规划（Evolution Programming，EP）[7]等。进化算法能有效处理传统优化算法难以解决的复杂问题，因此这些算法和设计一经发表就受到人们的青睐。

进化算法最主要的两大特点是群体搜索策略和个体之间相互交换信息。目前进化计算的应用领域已渗透到许多学科，同时应用实践又促进了进化计算的发展和完善[8-12]。

1.1 基本概念

1.1.1 收敛性

收敛性是进化计算研究的重要指标，直接关系到算法的应用价值[10，13]。收敛性的研究可为算法的发展提供理论依据和正确方向。

在算法设计中应尽量避免局部收敛或过早收敛。当算法陷入局部收敛时，产生的结果很可能不满足目标函数要求的最优解。

种群大小作为影响算法性能和收敛性的一个重要因素。种群太小不足以产生足够的样本点，种群太大，则增加计算难度、延长收敛时间。因此选择或设计算法时应充分运用已有的收敛性分析研究成果，从算法结构、控制参数选择、遗传算子的操作方式等方面综合考虑[14]。

1.1.2 适应度

进化计算中优化过程的求解主要依赖于个体的适应度值，适应度越好，越有利于生存进化。在优化过程中应尽量让适应度好的个体有更多机会繁殖后代。因此适应度函数的选取非常重要。适应度函数的选取直接影响到算法的收敛速度和能否找到最优解。一般而言，适应度函数的设计要综合考虑问题本身的要求及其值域的变化范围等[15，16]。

1.1.3 种群多样性

进化算法通过对大量个体进行优化操作推动种群进化，通常情况下种群的多样性越大，得到最优个体的几率越大，种群多样性越小，个体之间差异性越小，越容易发生过早收敛现象。所以种群多样性是进化的前提条件，种群只有在保持一定多样性的情况下才能进化。正确评价种群的多样性对进化算法的改进有着重要的指导作用。其中种群熵作为种群多样性评价的指标之一[17，18]。

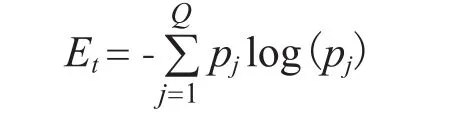
当种群中所有个体都相同，即Q=1时，熵取最小值，Emin=0。当Q=N时，熵取最大值，即Emax=log（N）。种群中个体类型越多，分配得越平均，熵越大。通过比较熵和最大熵的大小，分析种群多样性程度，进而判断进化算法的好坏。令α=Et/Emax，显然α∈[0,1]。α越大，种群多样性越大，反之，多样性越小。定义α≥0.5时，种群具有较大的种群多样性。

在选择或设计算法时，应首先考虑收敛性问题。在求最优解时，应综合考虑收敛性、适应度函数和种群多样性。适应度函数的选取直接影响收敛速度和能否得到最优解。最后还应保证种群的多样性。种群多样性越单一，算法越容易陷入局部最优，算法性能越差。

1.1.4 缺点

进化算法发展较早，应用广泛，其中遗传算法的应用最为广泛。但也存在一些缺点。传统算法的描述形式包括文字描述，代码，以及二进制，十进制和结构式编码等[19]。但这种描述、代码及编码形式不便于阅读理解。且只关注计算结果，往往忽视算法的中间过程。优化过程中各个染色体之间有什么关系，这种关系是否会影响进化结果?进化策略是否唯一?最优个体具有什么样的配对方式?若生成最优个体的配对染色体相似率较高，则不利于种群多样性的发展，也不利于种群进化。通过分析中间过程，将这个过程用复杂网络结构进行可视化，利用复杂网络技术找出能生成最优个体的相似率较低的染色体，推动种群进化。

因此复杂网络结构动力学能有效弥补这一缺点。受到2014年进化计算会议（IEEE CEC）上一篇名为《Evolutionary Algorithms Dynamics and its Hidden Complex Network Structures》文章的启发，可以将进化算法的优化过程用复杂网络动力学描述，将复杂的中间过程描述为清晰的网络结构图[2]。用复杂网络工具分析形成的结构图，进而控制算法。用基因片段相似度低的染色体产生最优个体，提高种群多样性。并对算法提出指导和改进意见。

2 复杂网络的研究发展

2.1 起源

复杂网络的研究起源于两篇标志性的论文：一篇是发表在Nature上的小世界网络（Small World Networks）[20]，另一篇是发表在Science上的无标度网络（Scale-free Networks）[21]。这两篇论文可以看作是复杂网络研究新纪元开始的标志。自然界中的许多系统都可以用复杂网络描述，同时，复杂网络可以量化和预测这个复杂多变的社会。如交通网、因特网、科学合作网、人类语言网、神经网、生态食物链网、细胞网、蛋白质网等。“复杂网络”一词来源于具有既不完全规则又不完全随机的连接模式，且表现出实质性和非平凡拓扑特征的网络。这些特征包括具有长长尾部的度分布、高聚类系数和分层结构。复杂网络是连接进化算法的另一个研究领域[3]。

复杂网络中，人们熟知的特征是无标度特性和小世界网络。这两个特征的研究和发现对复杂网络的研究有着非常重要的作用。其具体结构特点是具有幂率度分布的无标度网络和具有相对短的平均路径长度和高聚类系数的小世界网络[22]。

2.2 统计特征

2.2.1 度分布

复杂网络中，最基本的概念即为度：一个节点与其他节点连边的数目。

有向网络中，节点度可以分为出度（out-degree）和入度（in-degree）。出度指从该节点指向其他节点的边的数目，入度指其他节点指向该节点的边的数目。

度分布p（k）定义为网络中节点度为K的概率。节点度越大，对网络的影响力就越大。许多真实的网络度分布都遵循幂律分布，P(k)~k-γ（通常2＜=γ＜= 3）[23，24]。幂律分布也称为无标度分布。

度大的节点具有较大的度中心性，在网络中越重要。利用度中心性分析种群的停滞或早熟收敛现象[25]，进而保留最优个体，改善较差个体。

2.2.2 平均路径长度

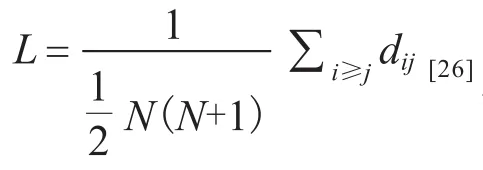
复杂网络具有相对较小的平均路径长度。计算进化算法形成的网络结构的平均路径长度判断进化算法能否用复杂网络或类似复杂网络的结构描述。

2.2.3 聚类系数

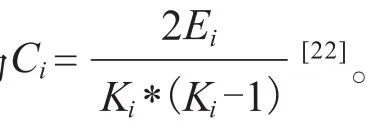
进化算法中，聚类可反映个体基因的分布。

2.2.4 介数

介数值来源于社会网络中对个体重要性的评估，度量特定节点和网络中其他节点长度的介数中心性定理首先是由Anthonisse（1971）和Freeman （1977）提出的。一个节点（边）的介数值表示所有的节点对之间通过该节点（边）的最短路径条数占所有最短路径的比例。因此，它能够刻画节点和边在网络中的重要程度[27]。

任意节点v的介数值定义如下：

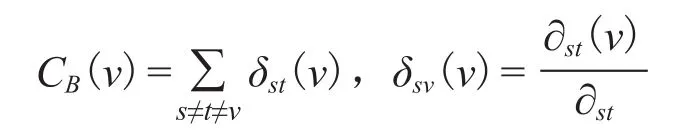
其中，∂st表示节点s到t的最短路径数目；∂st(v)为节点s到t的最短路径中经过节点v的最短路径数目[23]。也可以导出任意边e的介数计算公式。

由介数值的定义可知，计算节点和边的介数值，需要查找图中任意节点对之间的所有最短路径，因此计算方法具有非常高的计算复杂性。目前，已知最快的介数计算方法是Ulrik Brandes提出的。如果图中包含n个节点和e条边，如果是无权图，该算法的计算复杂性为O（en）；如果是加权图，则计算复杂性为O（en+n2log（n））。

具有相对高的介数中心性的节点，其适应度值相对较大。若节点的最大适应度值改变，则系统的介数中心性也随之改变。

2.3 研究现状

目前复杂网络的研究已经应用到许多领域。例如，文本抗毁性研究，城市网络信息空间局部聚集和整体联通的研究[28，29]。基于复杂网络理论，可有效分析复杂的综合电力问题、中国股票市场及网络游戏系统[29，30]。网络中节点重要性的分析与评价，可有效防止整个网络瘫痪[31]。基于复杂网络的高速公路网的结构和可靠性分析，有助于道路规划和突发事件的控制[32]。将复杂网络理论应用到城市交通网的信号控制研究中，寻找最优信号网络拓扑的演化过程。最优的信号配时和网络拓扑可缓解交通拥堵现象[33]。

在近几年的研究中，学者开始关注进化计算中隐含的复杂网络结构，并取得一些成果。2010年，Zelinka Ivan等人开始讨论进化计算和复杂网络的关系，研究讨论进化计算是否可以可视化或模拟成复杂网络。Zelinka Ivan等人发现进化计算可以可视化为类似于复杂网络的结构，而网络结构的构建依赖于多个因素。如果进化计算能被可视化，那么复杂网络的特点可用于描述算法或在以后的研究中控制算法的动态[34]。随后又对这两者之间的关系进行了进一步研究。在2011年，讨论了如何用复杂网络工具可视化进化算法。如果进化算法能被可视化，那么我们有理由相信复杂网络技术可用于控制进化算法[3，35，36]。在随后的几年，继续研究这两个研究领域的相互关系，并分析了差分进化算法、自组织迁移算法和遗传算法等的可视化结果[1，2，36-38]。

如果进化计算中蕴含着复杂网络结构，则存在一种改善进化算法的控制技术。但在以往的研究中没有考虑复杂网络动力学。而复杂网络动力学已成为研究的一个热点。

网络上的动力学行为称为建立在网络上的系统动态性质。研究复杂网络的拓扑结构也是为了理解和解释发生在网络上的动力学行为或过程。由于拓扑结构特征的统计量准确衡量了复杂网络的结构特性，故对复杂网络结构的研究有关键作用，因此历来是研究的热点所在。网络结构决定网络所承担的各种“功能”，这些功能是通过网络上运行的各种“动力学过程”实现的，故动力学过程的行为受拓扑结构的影响。可见，对网络结构的研究，是复杂网络其它一切研究的基础所在。不过，对复杂网络结构的研究，最终目的还是要用来解释网络上的动力学过程的行为[25]。值得注意的是，真实网络结构是不断变化的，网络上的动力学过程有可能反过来影响网络结构的变化，网络结构与网络动力学过程之间的复杂的相互影响和作用被称为“共同演化”，是近年来研究的热点。复杂网络拓扑结构对其传播动力学影响的研究是复杂网络研究的一大热点，具有许多现实的应用，如传染性疾病，计算机病毒，手机病毒，舆论在社会中的传播与扩散等，都可以看作是发生在网络上的某种传播动力学行为，通过对其传播行为的研究可以揭示其规律，制定相应的控制策略[39]。

复杂网络动力学的应用很广，但是用复杂网络动力学特性描述进化算法中间过程的文章还较少。本文将对网络动力学特征表示算法的优化过程进行简单分析，并讨论其可视化步骤。

3 进化计算中复杂网络的相关研究

本文的研究目的是用复杂网络的工具弥补进化计算忽略中间过程的缺点，及进化过程能否如复杂网络一样被可视化和模拟。若进化计算中蕴含着复杂网络结构，则存在分析和控制进化算法的某种技术。这两个看似完全不同的研究领域之间是否存在某种隐藏的结构关系，将成为进化计算研究领域的一大亮点[2]。

传统优化过程的描述形式大多为二进制编码、十进制编码或文字描述，不够清晰直观。传统方法常常忽略算法的中间过程，而中间过程对算法的结果有重大影响。从种群进化角度考虑，选择交叉的个体基因相似度高，不利于种群发展。然而用复杂网络工具可以避免此类问题。分析优化过程中染色体之间的相互关系，将这种关系可视化为类似于复杂网络的拓扑结构。这种可视化方法能够清晰直观的展现算法的优化过程。分析网络拓扑结构中染色体之间的关系，动态的展示算法的优化过程，促进种群进化。

3.1 实验设计

本文主要利用遗传算法研究优化过程中个体的相互关系，及这种相互关系是否能描述为复杂网络结构。选定的适应度函数为Ackley函数：

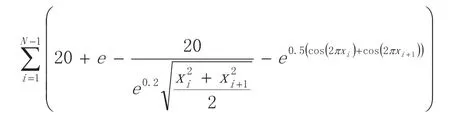
遗传算法的参数设置如表1所示。根据算法的优化过程，将算法重复运行100次，在100次迭代中10个个体的选择如图1所示。图1中的点代表每次迭代的最优位置。

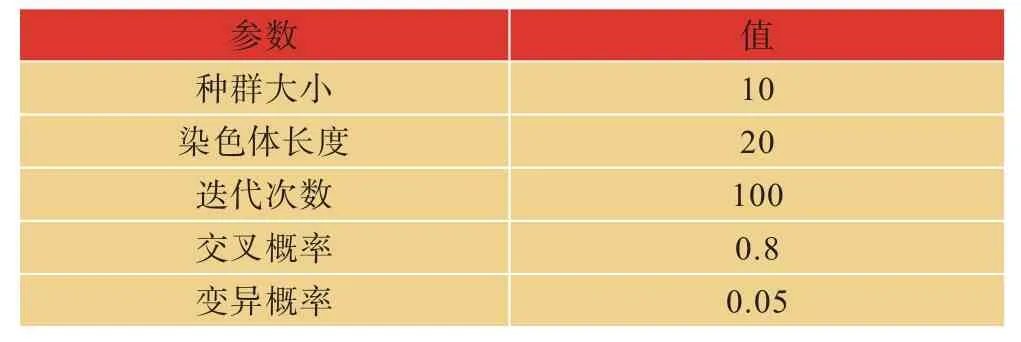
表1 参数设置Tab.1 Parameter Setting

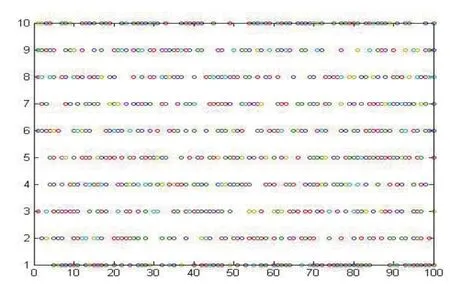
图1 算法迭代100次，个体的不同选择Fig.1 When algorithm runs 100 times，individuals have different choices

3.2 可视化

本文中可视化的原理遵循自然界中适者生存的原则。适应度越好的个体，被保留下来并成功产生后代的几率越大。进化算法描述为复杂网络动力学的步骤为。第一步：学习进化算法的规则和过程；第二步：分析个体之间的关系，如哪些个体可用于产生新个体，哪些个体从较差位置移动到较优位置。第三步：选择分析进化算法的复杂网络工具；第四步：用复杂网络动力学可视化算法的优化过程并分析形成的拓扑结构图。

随着算法的迭代，个体之间的关系不断变化，根据不断变化的染色体之间的关系建立网络拓扑结构模型。根据复杂网络动力学将算法的中间过程描述为网络结构的变化图（图2）。最后利用结构图验证各个算法的特点。

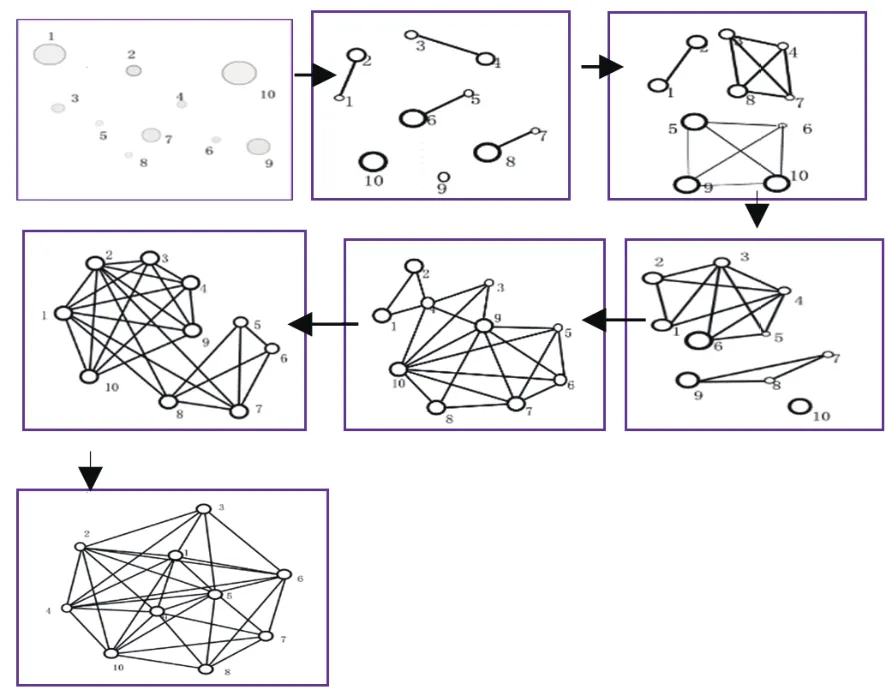
图2 算法优化过程的简单描述Fig.2 the simple description of optimization process

形成的网络结构是否符合复杂网络特性还需要进一步验证。将种群大小增大到100，利用上述可视化步骤得到如图3所示的典型网络结构图。然而图3是否符合复杂网络特点，还需要用复杂网络特性进行验证。

为确定图3的结构是否类似复杂网络，可用复杂网络的典型特征进行验证。例如具有长长尾部的度分布。分析图3中度的分布特征得度的分布图（图4）。从图4的拟合结果可知拖着长“尾”的分布曲线基本符合复杂网络的度分布特性。

真实网络结构的度分布一般符合幂律分布，即“富者越富”理论。幂律分布在双对数坐标下近似为一条直线。在图4得到的幂律分布图（图5）中除去距离较远的点外，前半部分的线性特性较弱，而后半部分近似于一条直线。因此可以说，图3的结构图类似于复杂网络结构。

由遗传算法的熵（图6）和100个个体在第100代时形成的网络结构（图7）可以看出，算法的熵在一定范围内来回波动，波动范围在0.8～1.4之间，即0.8＜Et＜1.4，0.4＜α＜0.7。因此遗传算法基本保持种群多样性，这与图7的结构图基本相符。图7的结构图中个体之间有相互关系但不是全连接。所以遗传算法能够有效找到最优解且基本保持种群多样性。

3.3 发展趋势

随着应用领域的扩展，进化计算的应用潜力以及复杂网络的应用研究已受到学者们的广泛关注。通过本文的研究对于复杂网络的深入研究以及进化计算的改进、优化和控制等应用方面具有一定的理论意义和应用价值。

目前关于进化计算中复杂网络结构的研究较少。这两个看似完全不同的研究领域，是否存在着某些隐藏的结构关系，将成为进化计算和复杂网络研究的一大热点。进化计算和复杂网络结构关系的发展前景是广阔迷人的。

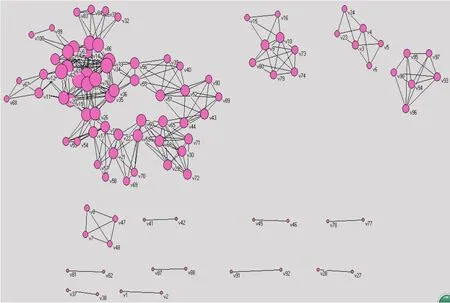
图3 遗传算法的可视化图。顶点指个体，边代表个体之间的关系。点越大，适应度值越大，个体在结构中的作用越大Fig.3 The visualization of genetic algorithm. Vertices refer to individuals，edges on behalf of the relationship between individuals.the greater dot which has better fitness has more important role in the structure

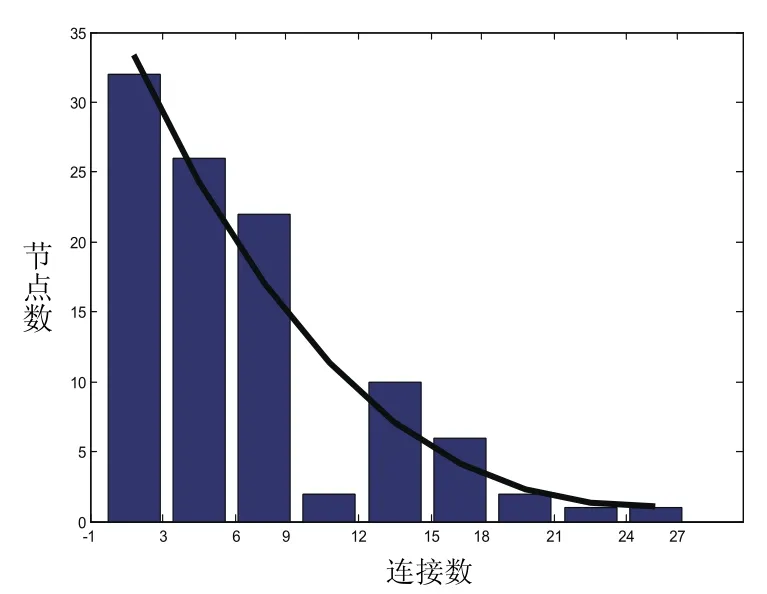
图4 度分布图Fig.4 degree distribution

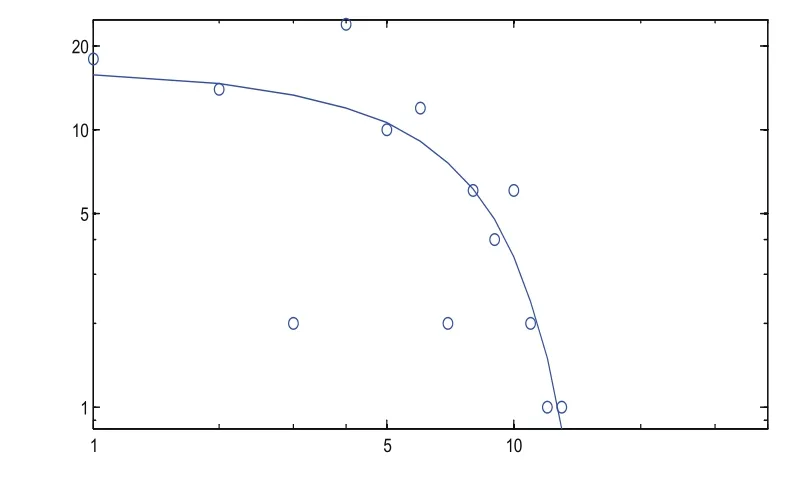
图5 幂律分布Fig.5 Power-law distribution

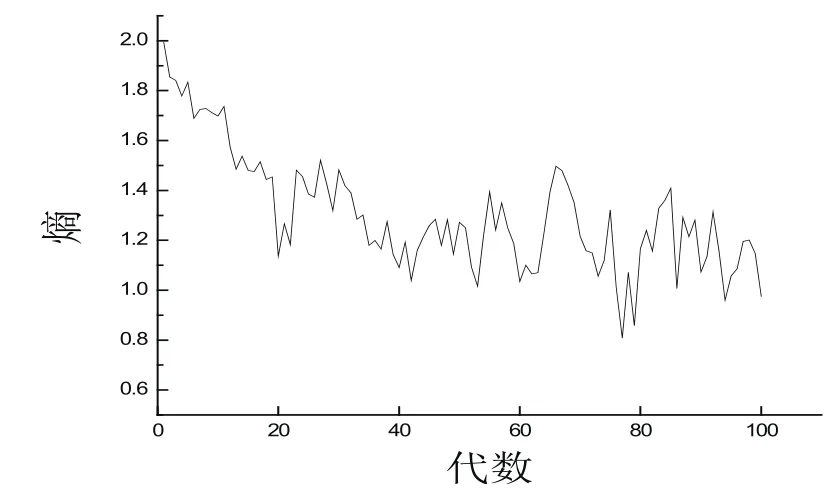
图6 熵Fig.6 Entropy

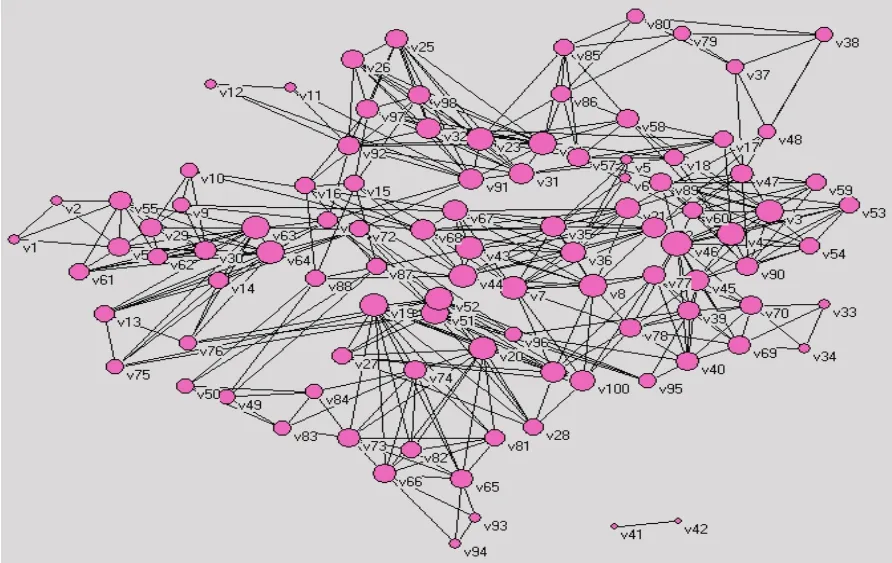
图7 第100代时，遗传算法形成的结构图Fig.7 the structure formed by GA，100th generation

4 结论

该研究可用于复杂网络是否存在于进化计算的分析和控制中。实验结果证明复杂网络结构或类似于复杂网络的结构蕴含于进化计算中，那么有理由相信存在一种控制或改进进化算法的技术。且复杂网络结构的出现依赖于多个因素，如种群大小，染色体长度，迭代次数等。

文中主要讨论了进化计算和复杂网络动力学的关系。重点分析了如何用复杂网络工具可视化进化算法，通过复杂网络特性可分析进化计算的特点并促进算法的进一步改善和发展。

致谢

感谢中国国家自然科学基金（41373101），河北省高校科学技术研究项目（QN20131081），河北省自然科学基金（F2015402070）和邯郸市科学技术研究与发展计划项目（1426109077-3）对本项目的支持。

[1] Zelinka I，Davendra D D，Chadli M，Senkerik R，Dao T T and Skanderova L. Evolutionary dynamics as the structure of complex networks[J]. Handbook of Optimization. Springer Berlin Heidelberg，2013：215-243.

[2] Zelinka I，Davendra D，Lampinen J，Senkerik R and Pluhacek M. Evolutionary algorithms dynamics and its hidden complex network structures. Evolutionary Computation （CEC） [J]. IEEE congress on evolutionary computation （CEC），Beijing，China，2014：3246-3251.

[3] Zelinka I，Davendra D，Senkerik R and Jasek R. Do evolutionary algorithm dynamics create complex network structures? [J]. Complex Systems，2011，20（2）：127-140.

[4] Holland J H. Adaptation in natural and artificial systems[J]. Control & Artificial Intelligence University of Michigan Press，1975，6（2）：126-137.

[5] Schwefel H P. Numerische optimierung von Computer-Modellen mittels der evolutionsstrategie[J]. Birkhäuser，Basel，1977，26.

[6] Rechenberg I. Cybernetic solution path of an experimental problem[J]. Royal Aircraft Establishment Library Translation，2010，1122.

[7] Fogel D B. Unearthing a fossil from the history of evolutionary computation[J]. Fundamenta Informaticae，1998，35（1-4），1-16.

[8] 汪慎文，丁立新，张文生，等. 差分进化算法研究进展[J]. 武汉大学学报（理学版），2014，60（4）：283-292. Wang Shen-Wen，Ding Li-Xin，Zhang Wen-Sheng，et al. Survey of differential evolution[J]. Journal of Wuhan University，2014，60（4）：283-292.

[9] 谢承旺，汪慎文，谢大同，等. 高维目标进化算法研究进展[J]. 武汉大学学报（共学版），2012，45（5）：636-642. Xie Cheng-Wang，Wang Shen-Wen，Xie Da-Ton，et al. Progress of research on many-objective algorithms[J]. Engineering journal of Wuhan University，2012，45（5）：636-642.

[10] 代真真. 基于统计学习方法的进化算法研究[硕士论文] [J]. 华东师范大学，上海，2014. Dai Zhen-Zhen. Evolution algorithm based on statistical learning method[J]. East china normal university，2014.

[11] 任丽娜，吕明月，刘爽爽，等. 基于蜂群算法优化的变桨距自抗扰控制器[J]. 新型工业化，2014（6）：43-48. Ren Lina，Lv Ming-yue，Liu Shuang-shuang，et al. Pitch control using active disturbance rejection controller based on colony optimization algorithm[J]. The Journal of New Industrialization，2014（6）：43-48.

[12] 王永辰，肖伸平，刘先亮. 基于改进自适应遗传算法的配电网重构[J]. 新型工业化，2015，5（8）：6-10. Wang Yong-chen，Xiao Shen-ping，Liu Xian-liang，et al. Distribution system reconfiguration based on improved genetic algorithm[J]. The Journal of New Industrialization，2015，5（8）：6-10.

[13] Bagrow J P and Bollt E M. Local method for detecting communities[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics，2005，72（2）：72-046108.

[14] 王莉. 遗传算法的收敛性统一[J]. 自动化技术与应用，2004，23（6）：16-19. Wang Li. A unified convergence criterion for genetic algorithms[J]. Automation Technology and Application，2004，23（6）：16-19.

[15] 金芬，孙春华，钟鸣. 遗传算法中适应度函数的改进[J]. 机械设计与制造，2010，3：218-219. Jin Fen，Sun Chun-Hua，and Zhong Ming. Improvement of fitness function in genetic algorithm[J]. Machinery Design & Manufacture，2010，3：218-219.

[16] Xuan D Y，Wang F L，Gao M H and Ma H Z. An improved fitness function of genetic algorithm[J]. Mathematics in Practice and Theory，2015，46（16）：232-238.

[17] 路景，周春艳. 基于种群多样性评价的自适应遗传算法[J]. 计算机仿真，2008，25（2）：206-231. Lu Jing and Zhou Chun-Yan. An adaptive genetic algorithm based on measurement of population diversity[J]. Computer Simulation，2008，25（2）：206-231.

[18] 张晓绩，戴冠中，徐乃平. 遗传算法种群多样性的分析研究[J]. 控制理论与应用.1998，15（1）：17-22. Zhang Xiao-Ji，Dai Guan-Zhong and Xu Nai-Ping. Study on diversity of population in genetic algorithms[J]. Control Theory andApplications，1998，1（1）：17-22.

[19] Lin Z and Yuming L U. Diversity of cellular genetic algorithm[J]. Electronic Science & Technology，2015.

[20] Watts DJ and Strogatz SH. Collective dynamics of 'small-world' networks[J]. Nature，1998，393（6684）：440-442.

[21] Barabasi A L and Albert R. Emergence of Scaling in Random Networks[J]. Science，1999，286（5439）：509-512.

[22] Wang X F and Chen G. Complex networks：small-world，scale-free and beyond[J]. IEEE Circuits & Systems Magazine，2003，3（1）：6-20.

[23] Wang J，Mo H，Wang F. Exploring the network structure and nodal centrality of China’s air transport network：A complex network approach[J]. Journal of Transport Geography，2011，19（4）：712-721.

[24] Lordan O，Sallan J M ，Simo P. Study of the topology and robustness of airline route networks from the complex network approach：a survey and research agenda[J]. Journal of transport geography，2014，37：112–120.

[25] Davendra D，Zelinka I，Senkerik R，et al. Complex network analysis of evolutionary algorithms applied to combinatorial optimization problem. Proceedings of the Fifth International Conference on Innovations in Bio-Inspired Computing and Applications IBICA 2014[J]. Springer International Publishing，2014，141-150.

[26] 吴增海. 社交网络模型的研究[博士论文] [J]. 中国科学技术大学，合肥，2012. Wu Zeng-Hai. Research on the model of social network[J]. University of Science and Technology of China，2012.

[27] Chen Y Z，Huang Z G ，Lai Y C. Controlling extreme events on complex networks[J]. Scientific Reports，2014. 4：6121-6121.

[28] 申艳光，王杰，生龙，等. 基于复杂网络的文本抗毁性分析[J]. 计算机应用研究，2015，32（3）：679-682. Shen Yan-Guang，Wang Jie，Sheng Long ，et al. Text invulnerability analysis based on complex network[J]. Computer Application Research，2015，32（3）：679-682.

[29] 王旭文. 复杂网络上的演化博弈及可控性研究[博士论文] [J]. 中国科学技术大学，合肥，2015. Wang Xu-Wen. Evolutionary games and controllability on complex networks[J]. University of science and technology of china，2015.

[30] 庄新田，张鼎，苑莹，庄霄威. 中国股市复杂网络中的分形特征[J]. 系统工程理论与实践，2015，35（2）：273-282. Zhuang Xin-Tian，Zhang Ding，Yuan Ying and Zhuang Xiao-Wei. Fractal characteristic of the Chinese stock market complex network[J]. Systems Engineering-Theory & Practice，2015，35（2）：273-282.

[31] 秦李，杨子龙，黄曙光. 复杂网络的节点重要性综合评价[J]. 计算机科学，2015，42（2）：60-64. Qin Li，Yang Zi-Long and Huang Shu-Guang. Systhesis evaluation method for node importance in complex networks[J]. Computer science，2015，42（2）：60-64.

[32] Dai H，Yao E，Lu N，Bian K and Zhang B. Freeway network connective reliability analysis based complex network approach[J]. Procedia Engineering，2016，137：372-381.

[33] Li S B，Li Y，Fu B B and Dang W X. Study on simulation optimization of dynamic traffic signal based on complex networks[J]. Procedia Engineering，2016，137：1-10. ，.

[34] Zelinka I，Davendra D，SnáŠEl V，Jašek R，Šenkerík R and Oplatková Z. Preliminary investigation on relations between complex networks and evolutionary algorithms dynamics[J]. Computer Information Systems and Industrial Management Applications （CISIM），2010 International Conference on. IEEE，2010，148-153.

[35] Klimkova E and Fekiac J. Vizualization of evolutionary algorithms by means of complex networks[J]. Annals of Daaam & Proceedings，2011，22（1）：1521-1522.

[36] Zelinka I. Investigation on relationship between complex networks and evolutionary algorithms dynamics[J]. Numerical Analysis & Applied Mathematics Icna. AIP Publishing，2011，1011-1014.

[37] Zelinka I. On Analysis and Performance Improvement of Evolutionary Algorithms Based on its Complex Network Structure. Advances in Artificial Intelligence and Soft Computing[J]. Springer International Publishing，2015，389-400.

[38] Zelinka I. A survey on evolutionary algorithms dynamics and its complexity – Mutual relations，past，present and future[J]. Swarm & Evolutionary Computation，2015，25：2-14.

[39] 姚新，陈国良，徐惠敏，等. 进化算法研究进展[J]. 计算机学报，1995，18（9）：694-706. Yao Xin，Chen Guo-Liang，Xu Hui-Min，et al. A survey of evolutionary algorithms[J]. Chinese Journal of Computers，1995，18（9）：694-706．

Research on the Relationship Between Evolutionary Algorithms and Complex Network Structure

SHENG Long, GUANG Xiao-yun
(School of Information Electrical Engineering, Hebei University of Engineering, Hebei Handan 056038)

Evolutionary algorithm is a kind of optimization algorithms which based on Darwinism and imitated the process of survival of the fittest. After the evolution of several generations, the finally optimal solution will be obtained. But the description of evolutionary process is not clear, and people only focus on results, often ignores the intermediate process. Complex network structure can effectively compensate for the shortcomings of evolutionary algorithm. The relationship among individuals is described as dynamic processes, and complex network structure is discussed by analyzing the optimization process. Finally using the complex network technology to control or improve algorithm. Set the relevant parameters of dynamic experiment and verify whether the network has complex network characteristics. The result of experiments indicates that the optimization process of evolutionary computation can be described as complex networks structure or similar to the structure of complex networks. For further study of complex networks and the improvement, optimization and control of evolutionary algorithms, it has certain theoretical significance and practical value.

Evolutionary algorithm; Complex network; Dynamic; Networks structure; Optimization

生龙，广晓芸.进化计算与复杂网络结构关系的研究[J]. 新型工业化，2016，6（11）：1-9.

10.19335/j.cnki.2095-6649.2016.11.001

: SHENG Long, GUANG Xiao-yun. Research on the Relationship Between Evolutionary Algorithms and Complex Network Structure[J]. The Journal of New Industrialization, 2016, 6(11) : 1-9.

中国国家自然科学基金（NO. 41373101），河北省高校科学技术研究项目（No. QN2013 1081），河北省自然科学基金（No. F2015402070），邯郸市科学技术研究与发展计划项目（NO. 1426109077-3）

生龙（1982-），男，博士，讲师，计算机学会（CCF）会员,主要研究领域为复杂网络、机器学习、数据挖掘

广晓芸（1990-），女，硕士研究生，计算机学会（CCF）会员（NO.51300G）,主要研究领域为复杂网络