整体成型天线罩风载荷计算方法

白雪寒，潘永生，杨成

(1.哈尔滨哈玻拓普复合材料有限公司，哈尔滨150036)(2.海军驻哈尔滨地区军事代表室，哈尔滨150000)

整体成型天线罩风载荷计算方法

白雪寒1，潘永生2，杨成1

(1.哈尔滨哈玻拓普复合材料有限公司，哈尔滨150036)(2.海军驻哈尔滨地区军事代表室，哈尔滨150000)

确定准确的整体成型天线罩风载荷的拟合函数，对目前的仿真工作有重要的工程意义。本文从《建筑载荷规范》中圆截面构筑物的体型系数出发，利用matlab软件拟合出圆截面环向角度下的风载荷加载函数。通过对不同阶数下拟合成的傅里叶级数方程的函数曲线与《建筑载荷规范》中的相应数据点进行对比，分析各阶拟合方程的不同之处及对仿真计算可能产生的影响，最终确定各拟合结果的优劣。

整体成型天线罩;风载荷;方程拟合;整体评估

1　引言

随着军队和民营单位对雷达探测精度要求的不断提高，对雷达配套天线罩产品的电性能指标要求也变得愈加苛刻。常规的分块式雷达天线罩往往存在较宽较长的实心玻璃钢连接边肋和空间阵列的金属螺栓，且产品由于手糊工艺含胶量难以准确控制，通常不能保障蒙皮的厚度均匀。以上情况对电性能产生的影响，直接导致常规工艺下分块天线罩的性能已经难以满足当前指标要求。

鉴于这种情况，我公司开发了采用整体成型工艺生产的新型雷达天线罩。与常规的分块式雷达天线罩不同，整体成型雷达天线罩不存在空间上的实心边肋和金属螺栓阵列，而含胶量方面也能够进行有效控制，较好的保障产品的均一性。经测试产品能够满足顾客当前所提出的各项电性能指标要求。

然而整体成型天线罩却存在其结构上不足。首先，常规分块式天线罩的空间实心边肋能够对整罩起一定的加强作用，而在整体成型天线罩上则不存在这样的实心边肋结构;其次，整体成型天线罩通常采用类圆顶柱形或类圆顶锥形的设计结构，从形态上看其稳定性要低于常规截球形式的天线罩。而且目前针对整体成型天线罩这类非常规形状的构筑物外表面风载并没有明确的加载函数，能否选取准确的风载荷方程对整体成型天线罩进行加载其结构计算是至关重要的。

本文的主要内容是针对整体成型天线罩的具体特征，选用合适的风载荷加载方程对天线罩柱段圆截面上的环向体型系数进行描述。

2　柱段风载荷拟合数据

根据整体成型天线罩的结构特点，上段为50%的球状穹顶，在此处不进行具体的分析;下段为圆柱形，根据2012年发布实施的《建筑结构载荷规范GB5009-2012》中对于柱形结构风载加载的要求来进行拟合计算，选取适当的加载方程。

《建筑结构载荷规范GB5009-2012》中对柱段风载荷体形系数的规定是按照柱段的不同的H/d (高度/直径)而相应确定的，具体指标如下:中对圆截面构筑物的局部计算式表面分布的体型系数:

表1　建筑载荷规范风压加载定义

根据柱形天线罩的截面特征，将拟合的方程利用傅里叶级数的形式表达出来。由于整体成型天线罩高宽比通常不大于1，拟定选择规范中H/d=1尺寸所对应的体型系数来进行拟合比较恰当。将上述尺寸的构筑物体形系数分别利用2阶、4阶和5阶傅里叶级数进行拟合并进行横向对比。

其不同阶数的具体表现形式如下:

拟合后的方程中各项参数如表2:

表2　风载各阶拟合函数相关参数

3　拟合结果分析

根据以上参数组成的方程，将其曲线带入与《建筑载荷规范》中相应坐标点进行对比分析，得到图1。

图1　2阶、4阶、5阶傅里叶方程与建筑载荷规范坐标点比较

对以上拟合方程的输出的图像进行横向对比。从迎风面上看，0°～30°间正压差距并不大，5阶傅里叶级数方程拟合略精确于2阶和4阶傅里叶方程;随着进入负压区，体形系数不断增大，3条曲线开始发生不同程度的偏差，虽然整体的偏差并不大，但是也并没有某段曲线能够完全匹配建筑载荷规范的要求;在迎风面两侧约60°～90°的范围内，尤其是在75°和90°两个点上，三种不同阶数的傅里叶方程的差值达到最大，从精度判断可以认为在这两个点上，5阶傅里叶积分的精度要高于4阶，4阶傅里叶积分的精度要高于2阶，其具体原因可以认为是高阶的傅里叶积分函数能够更适应存在突变点的情况;在90°～120°之间，《建筑载荷规范》中体形系数由之前的两个突变点逐渐趋向平滑，5阶傅里叶积分函数的优势减弱，相对的4阶傅里叶积分函数的拟合结果反而相对准确;在120°～180°之间，5阶傅里叶积分函数在定点程上下反复波动状态，相对而言，4阶和2阶傅里叶函数则表现出更好的匹配结果。

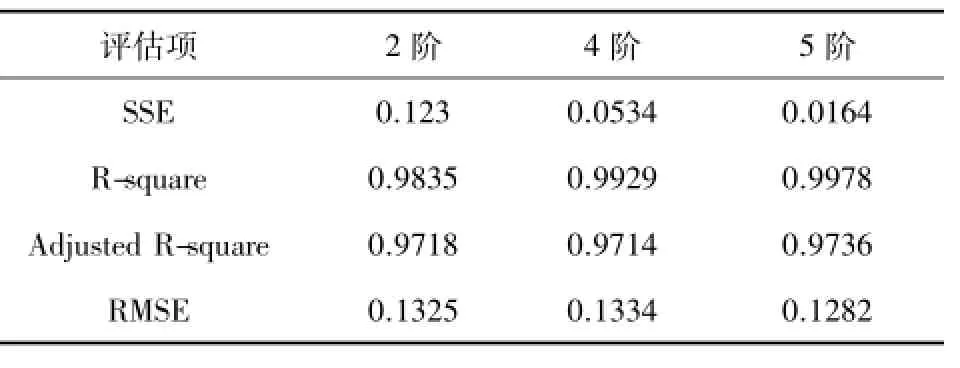
表3　风载各阶拟合函数参数评估

对于拟合曲线好坏的主要是通过SSE(和方差)、R-square(确定系数)和RMSE(均方根)三项进行评判的。从当前的拟合结果上看，表示整体拟合水平的R-square和RMSE数据中，三种方程的之间的差距并不明显;然而在表示单点拟合程度的SSE上，5阶傅里叶级数方程的对应值明显优于其他两组方程。这也正对应之前在75°和90°两个数据点上判断，5阶的傅里叶积分在这两个数据点上单点的偏差要小于其余两阶的情况。

4　结语

综上所述，本文旨在通过傅里叶级数方程的表现手段将《建筑载荷规范》中圆截面构筑物的外表面环向角度下的体型系数加以描述，并使之能够达到适宜有限元计算的程度。经分析，从稳定性角度考虑，对稳定性起较大影响的通常是迎风面的正压区，几种不同阶数的傅里叶方程拟合的函数在正压区域上差别不大;但从最大应力、应变方面考虑，最大应力产生的区域都在侧面的负压区，且负压区对迎风面的形变也会起较大作用，而5阶傅里叶级数对负压区域的描述精度则要略高于2阶和4阶的情况。

故而可以判断，在对整体成型天线罩的各项结构计算数据精度都要求较高的情况下，可以利用5阶傅里叶级数方程的拟合结果来对风载情况下的柱段外表面的载荷进行描述;较低阶数的拟合结果只能适用于稳定性评估，如在应力及形变计算中使用必须充分考虑到加载存在误差所造成的影响。

［1］中华人民共和国住房和城乡建设部.建筑载荷规范［M］.中国建筑工业出版社，2012:30-63.

［2］哈玻.玻璃钢地面雷达天线罩［M］.哈尔滨:哈尔滨工程大学出版社，2002:38-107.

The Algorithm of Wind Load for the Integral Moulding Radome

BAI Xuehan1，PAN Yongsheng2，YANG Cheng1
(1.Harbin Topfrp Composite Co.，Ltd.，Harbin 150036)
(2.The Naval Military Representatives Office Positioned in Harbin，Harbin，150000)

Determining the function of wind load of the integral moulding radome has great significance to thefuture work of simulating analysis.In this paper the Pressure-Anglefunction of the wind load will be fitted with matlab according to Load Code for the Design of Building Structures，then compare the function curves of different Fourier equations with the point of shape coefficient on circular cross-section.By summarizing assessment of the differences between each fitted equation and the influence to the calculation，the most suitable Fourier equation will be ensured.

sintergral moulding radome;wind load;function fitting;overall assessment

2016-01-15)

白雪寒(1990-)，男，黑龙江人，学士，结构工程师。研究方向:复合材料产品结构设计。

E-mail:hrbfrp_bxh@163.com.