扰动环境下作业车间网络多瓶颈识别方法研究

李晓娟,孙文磊,袁逸萍,李华华

(新疆大学机械工程学院,830047,乌鲁木齐)



扰动环境下作业车间网络多瓶颈识别方法研究

李晓娟,孙文磊,袁逸萍,李华华

(新疆大学机械工程学院,830047,乌鲁木齐)

针对扰动环境下作业车间多瓶颈识别困难、瓶颈漂移后的瓶颈识别缺乏全局性和实效性这一问题,构建了基于网络特性的多瓶颈动态识别方法。首先,根据设备工装、工艺路线、物流路径以及产品配置等多层次生产数据,构造作业车间网络模型;其次,建立作业车间网络动力学方程,获取扰动因素流转的判定依据。对瓶颈内涵进行扩充,综合考虑节点自身动力学特性、节点间拓扑耦合影响机理及扰动在生产网络中的传播机制,建立基于耦合映射格子(CML)的瓶颈识别算法,实现作业车间瓶颈的量化描述和连续预测;最后,对某机电企业作业车间进行瓶颈的动态监控和预测。结果表明:在扰动环境下,CML模型能够较好地预测各工作站瓶颈度走势,其中工作站R1平均瓶颈度为1.12,瓶颈持续时间长达40 h;工作站R3的平均瓶颈度为1.05,瓶颈持续时间为10 h;工作站R1、R3首先成为系统的瓶颈,随着加工进度的推移,工作站R1和R24交替成为系统瓶颈。研究结果与该企业实际情况具有很好的一致性,验证了该方法的有效性和准确性。

作业车间;扰动环境;复杂网络;CML模型;瓶颈识别

作业车间包含大量的资源节点,不仅表现出节点间存在复杂相互作用、依赖关系的定常周期运动,更表现出一种普遍意义的形式,即无序的混沌。在实际生产过程中,各种随机扰动因素的存在都会引起车间工况发生动态变化,导致生产瓶颈频繁漂移。如何在扰动环境下,进行作业车间瓶颈时空特性的识别,进而构建新型、快速、准确的动态瓶颈识别方法是资源优化配置的首要任务。为了保证资源的合理配置,探索扰动环境下的瓶颈识别问题成为研究的首要重点。文献[1]针对离散事件系统的瞬时瓶颈和平均瓶颈,利用设备持续活性时间进行识别;文献[2]使用在线数据驱动方法,找出机器在指定时期阻塞和饥饿出现的“拐点”识别该时期的瓶颈;文献[3]通过仿真方法获取机器利用率、机器加工利用因子、机器生产瓶颈率3个指标,并制定if-then评判规则进行瓶颈识别;文献[4]基于聚类思想及多属性决策理论提出了作业车间瓶颈簇的识别方法,识别包含瓶颈资源的瓶颈簇;文献[5]针对大规模作业车间生产调度问题,以系统作业目标对各个机器上调度方案变化的敏感度为指标,采用正交试验识别瓶颈设备;文献[6]提出将物料流瓶颈度用于表征制造单元阻碍制造车间物料流流动平顺程度的指标,针对不确定环境下物料流瓶颈进行了识别;文献[7]对不确定环境下作业车间重调度问题进行了研究。

综上所述,对不确定环境下的作业车间瓶颈识别研究是十分有意义的,但存在以下问题:①依据瓶颈设备的外部表现特征进行识别,属于瓶颈静态识别方法,识别简单直观,当系统处于不确定环境、存在多瓶颈工况时,其识别的瓶颈并不一定是真正的瓶颈;②利用仿真和智能优化算法分析的优势进行瓶颈识别和调度优化,可操作性强,但是该类研究严重依赖模型,当系统处于不确定环境时,该方法的响应性慢,推广具有一定的限制性;③在不确定环境下,基于动态响应的调度方法是将调度由事后追逐向事先控制转变的实时动态响应,但实现过程较为复杂,从而使得该方法的操作难度大,且当系统出现多个瓶颈时,主次瓶颈并不总能得到有效的辨识。为了获得长期的生产决策支持,本文创新性地提出生产瓶颈研究思路和方法成为制造企业提高效益的迫切需求。

复杂网络是研究复杂系统的一种角度和方法,它关注不同复杂系统的结构、功能及相互耦合关系,是理解复杂系统性质和功能的基础。目前,将复杂网络应用到制造业进行相关基础研究才刚刚起步。文献[8]运用复杂网络对流程工业中物料流动进行失效分析。文献[9-10]将复杂网络理论用于动态物流网络异常的检测,同时针对经典单元制造企业组织结构设计问题,提出了制造系统网络自组织结构的新方法。文献[11]基于复杂网络理论建立了复杂制造系统演化模型。文献[12]给出了6种生产网络动态瓶颈的定义,并采用约束理论和物流分析研究瓶颈辨识问题。文献[13]以工业汽轮机产品族为研究对象,建立了基于复杂机械产品族的零部件关系网络,并证明了该网络的小世界特性和无标度特性,同时发现产品族网络具有分层、模块性等显著特点。文献[14]将复杂网络理论用于制造系统瓶颈识别,从新的角度提出了瓶颈动态识别的新方法。可见,利用复杂网络对制造系统的固有特性进行分析和研究是可行的。

本文以作业车间为研究对象,提取蕴含设备工装、工艺路线、物流路径以及产品配置等多个层次的生产数据,建立作业车间网络(JSN)模型及网络动力学方程。定义扰动环境下瓶颈的概念,提出综合考虑节点自身动力学特性、节点间拓扑耦合影响机理及扰动在生产网络中的传播机制的瓶颈辨识方法,从更贴合作业车间系统实际的角度进行瓶颈时空特性识别。实际观察结果与时域仿真比对验证了方法的有效性,为求解复杂生产环境下生产调度优化问题提供新思路和新方法。

1 作业车间网络模型

1.1 作业车间网络描述

作业车间安排h种共n个工件在m台设备上进行加工。工件Ji(i∈{1,2,…,n})按照给定的工艺路线进行加工,其中工件Ji由Oi道工序组成,Oij为Ji的第j道工序。各工序之间存在工艺上的先后时序约束,每道工序对应需求的生产资源及该资源上的加工时间是已确定的。Tijr为第i个零件Ji的第j道工序在设备r的标准加工时间。

如果将作业车间系统中涉及的每一个工作站(设备、工装、质量控制点等)作为一个节点,将节点间可能存在的工艺路线、物流路径作为边,则作业车间生产系统构成了一个多任务有向加权网络,如图1所示。任务的动态增减触发网络结构的变化,JSN模型是依据订单的任务分解所具有的共性特征进行建模的结果。

首先,对网络模态进行降维处理,完成二维网络向一维网络的投影,即任务层向工作站层的映射,规则如下。

(1)同一个任务中的工序在一般情况下存在时间上的约束,因此同一个任务中的不同工序通常不能同时进行加工。在这种情况下,这个任务的工序所对应的所有工作站就构成了一个完全连通的子图。

(2)不同任务的不同工序之间常常会出现抢占同一个工作站的情况,在这种情况下,将该工作站加入每一个单一任务所对应工作站的完全连通图。这样,所有任务和工作站之间的对应合作关系就可以看作由多个工作站构成的网络图。图1a是描述这种生产网络的双粒子图。当一项工序需要占用不同的工作站时,它们之间都连接一条边,同时两个工作站之间也连接一条边,如图1b所示。

(a)订单-工作站分图示意 (b)订单-工作站映射关系图1 生产车间网络映射关系

根据作业车间特征,提出统一的数据集合,表达JSN的数据结构,使生产约束条件通过点、边和映射关系予以充分反映。模型中的参数分别表示:节点数,连边数,映射关系,订单属性,边权的集合,节点服务能力。该数据结构可实现对作业车间的网络化映射,按照需要简化网络。

在网络描述层面,网络之间的数据结构定义为

式中:R表示节点集合,R∈{1,2,…,r,…,m};E表示连边的集合;M(td)表示任务与节点映射关系;U表示订单集合,U={1,2,…,x};wij边权的集合,表示制造任务占用制造资源的时间负载,即节点i和节点j之间连边的权重大小;Qr表示节点r在额定工作时间内能持续提供服务的能力,Qr∈[0,1],计算式为

(1)

其中,Ter、Tcr、Tqr分别表示设备r由于设备故障、更换工装卡具、加工质量3项问题引起的服务损失时间;Tr为设备r每个工作日内的额定工作时间。

基于上述定义,可显著简化作业车间网络的复杂度,避免发生维数灾难,极大减少了后期网络数据计算量。

1.2 网络化特征提取

定义1 扰动因素是指在不确定环境下,作业车间网络内部引起的节点自身产能和负载相应改变,导致节点间连接性质改变、节点间耦合强度增减等各种因素。

定义2 瓶颈是指在作业车间网络中拥有重要位置、在很大程度上可以控制制造信息的传播路径走向、改变制造信息传播范围的节点。

定义3 瓶颈度是指节点在各种不确定因素共同影响下成为瓶颈的能力,它是节点固有的一种动态特性,用于描述节点对制造网络的直接影响力。

考虑到作业车间的网络结构,不同的扰动因素都会给瓶颈的时空特性带来影响,文中抽取了节点度、节点负载两个重要参数用于瓶颈识别,具体定义如下。

(1)节点度

入度:入度是指JSN中有多少上游节点直接与该节点相连,公式为

(2)

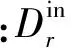
出度:出度是指在JSN中有多少下游节点被直接连接到所观察的节点,公式为

(3)

节点度:节点度是该节点入度和出度之和,是表征节点局部重要特征的指标之一,公式为

(4)

在JSN中,节点的度值具有重要的工程意义,该值越高,表示该节点参与的加工任务就越多,节点的利用率和重要性就越高。

(2)节点负载

节点负载是指所有待处理的零件占用第r个工作站的时间总和与节点r额定工作时间的比值

(5)

式中:h为总的零件类型;qi为零件Ji的数量;Nf为零件Ji的处理次数;Aijr为设备系数,如果零件Ji的第j道工序可以在工作站r上完成,则Aijr=1,反之Aijr=0;Tijr为设备r处理第i个零件Ji的第j道工序的标准时间。

2 扰动因素分析

2.1 扰动因素传播特性

对作业车间网络拓扑结构特性研究发现:网络度分布与强度分布均介于指数分布和幂律分布之间,而点权分布与典型的幂率分布特性更为相近[15]。因此,加工车间系统可能就处于一种特殊的敏感状态,微小的扰动变化都可能会不断被放大、流转,进而扩张至整个网络,影响整个系统的有效产出。

(1)扰动因素的传播引起网络节点负载动态变化。JSN网络节点负载的分布是由加工任务的工艺路径及所需资源的加工时间所决定的。当扰动发生时,原本按生产计划通过该路径的负载(物料流、信息流等)有可能会重新选择路径或就此中断。那么扰动的发生即会导致网络中的节点负载发生一次更新。随着扰动的不断产生与推进,网络节点负载也相应动态变化。

(2)扰动因素传播引起瓶颈时空特性的变化。不同的扰动都有可能导致车间生产活动的波动,这相当于在t时刻给JSN网络施加一个外部扰动,若节点r在t时刻受扰动因素影响,节点瓶颈度发生变化,那么在下一时刻,所有节点r的邻接节点都将受到t时刻节点r瓶颈状态的影响。随着扰动的传播,网络瓶颈的数量和位置也会不断发生变化,在某时刻可能存在多个瓶颈,且瓶颈会发生动态漂移。

(3)扰动因素传播引起网络结构耦合关系的变化。扰动的加载无疑会导致现有作业车间网络结构耦合关系发生变化,不同的扰动强度对网络结构耦合影响差异也不同,这取决于扰动因素对网络节点关键路径的影响程度。

2.2 扰动因素强度

扰动因素强度取决于扰动因素对关键路径的影响程度,本文根据工艺路线相关性理论,将扰动强度集合划归为3类,即强相关扰动、弱相关扰动和非相关扰动。

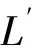
定义4 强相关扰动。若存在C、fi、Li满足P(fi,Li)>0,Li依赖fi并受到fi的直接影响,称fi为强相关扰动。扰动因素fi是强相关,当且仅当

(6)

强相关扰动是指扰动因素路径对现有节点加工进度的关键路径构成直接影响,若发生强相关扰动,必然影响节点的关键路径的加工进度。

(7)

弱相关扰动是指在一定条件下,扰动因素发生有可能会影响到节点加工进度的关键路径,但不一定是存在的。

定义6 非相关扰动。若存在扰动fi既不是强相关也不是弱相关,称fi为非相关扰动。扰动因素fi是非相关,当且仅当

(8)

非相关扰动是指扰动因素路径发生在关键路径节点之外,不影响整体加工进度。

随着加工进度的推进,每个工作站瓶颈度都会由于扰动的影响而不断发生变化,系统瓶颈的数量和位置也不断变化。

3 基于CML的加权网络瓶颈识别

CML(耦合映象格子)模型[16]能从物理的角度出发将复杂系统时间和空间变量离散化,但状态变量仍保持连续,在认识时空系统的动力学特征及规律方面具有优良的时空和混沌特性,同时又容易进行数值和解析处理。目前,该模型已成为非线性时空系统混沌的一个研究分支,被广泛用于研究复杂系统的时空动力学行为。例如,本文所分析的作业车间系统同样具有混沌和紊乱特性,其制造环境是不断变化的,含有很多随机和不确定因素。这些不确定因素在不停的产生、传播和过时。工作站负载、瓶颈时空特性以及网络结构耦合关系的变化使得作业车间网络的动力学特性也不断变化,制造信息更是表现出混沌和紊乱特性。考虑到CML模型从本质上显示出网络中扰动因素传播的动力学特性,本文采用CML模型表现出来的动力学行为去认识作业车间系统的瓶颈时空特征及规律。

3.1 基于CML的加权网络扰动模型

结合前人在CML模型上的研究成果,同时采用控制论中的动力学理论,建立作业车间制造过程扰动因素传播动力学模型。该模型包含3部分动力学行为。

(1)工作站节点自身动力学行为,公式为

(9)

式中:xr(t)表示t时刻节点r的瓶颈度;网络拓扑耦合系数ε1以及加权负载分布耦合系数ε2分别用来表征扰动加载前后网络结构耦合关系的差异,ε2通过扰动发生的节点及路径对关键路径的影响程度进行确定,ε1,ε2∈(0,1),ε1+ε2<1;非线性函数f(·)表示网络中的单个工作站代表一个混沌动力系统,在这里选用混沌Logistic映射f(x)=4x(1-x),其物理意义可表征为工作站节点生产能力约束的演化规律。

(2)网络拓扑耦合特性动力学行为,公式为

(10)

该部分表示具有混沌动力系统特征的各工作站相互协作组成一个有效的JSN动态网络,该网络节点间的耦合关系可描述网络拓扑耦合特性动力学行为。不同的工作站由于耦合关系不同而可能产生具有完全不同动力学的网络结构。节点的连接信息用A=(aij)N×N来表示。

(3)扰动因素传播动力学行为。作业车间生产过程中由于紧急插单、订单交货期变更或者人为等不确定因素的影响而可能导致车间生产活动的波动,这相当于在t时刻给JSN网络施加一个外部扰动,表达式为

(11)

式中:wij是节点i和节点j之间连边的权重;wr是节点r的负载。

总体而言,若节点r在t-1时刻瓶颈度受扰动因素影响发生变化,那么在t时刻,所有与节点r邻接的节点瓶颈度都将受到t-1时刻节点r的瓶颈度xr(t)的影响

(12)

网络瓶颈发生的初始时间会随着扰动耦合强度ε2的增大而提前,瓶颈漂移的速度也会随之增快。

3.2 基于CML的加权网络瓶颈识别算法

以设备表征的工艺路线、满足订单优先关系,建立具有复杂特性的作业车间网络结构模型。基于网络模型,提取与瓶颈度相关的网络特征参数(度、聚类系数、网络效率),基于CML的加权网络扰动模型,对节点在当前的状态值进行仿真计算得出下一时刻状态值,引发新一轮的节点瓶颈度波动。在下一时刻瓶颈状态值越大的节点,成为瓶颈的可能性越大。依据瓶颈度判定标准,实现瓶颈单元、非瓶颈单元以及主次瓶颈的识别。随着加工进度的推进,这个过程反复进行,各节点状态值不断发生变化,可能引发多瓶颈共存和瓶颈漂移现象。识别方法流程如图2所示,其中χ为瓶颈判断标准,k为瓶颈个数。

算法步骤如下:

Step 1:建立网络模型;

Step 2:根据式(2)～式(4)计算节点度D(r);

Step 3:根据式(5)计算节点的负载Wr;

Step 4:根据式(6)～式(8)计算扰动因素强度ε2;

Step 5:根据式(12)计算第r个节点在JSN模型中的瓶颈度xr(t);

Step 6:根据χ值判断节点瓶颈状态;

End:在Step 6中的结果输出即为节点瓶颈状态评估值。

图2 作业车间网络瓶颈识别方法流程

4 实例验证

4.1 数据处理

以某机电产品企业A车间数据集作为模型研究实例,该企业车间组织形式遵循作业车间原则,所采集实验数据均为该车间制造执行系统(MES)系统真实反馈数据。该车间共有35个工作站Ri,i={1,2,…,35},生产A、B、C和D 4类典型零件,每天工作8 h。假设F1、F2为该工作车间生产过程中最为频繁出现的两个扰动因素,分别为紧急订单与订单交货期变更。提取数据如下:表1所示为每种零件在各工作站的标准处理时间、准备时间和各工作站服务能力;表2所示为每天的计划生产任务量。假定该车间运输设备充裕,不存在物流运输瓶颈。

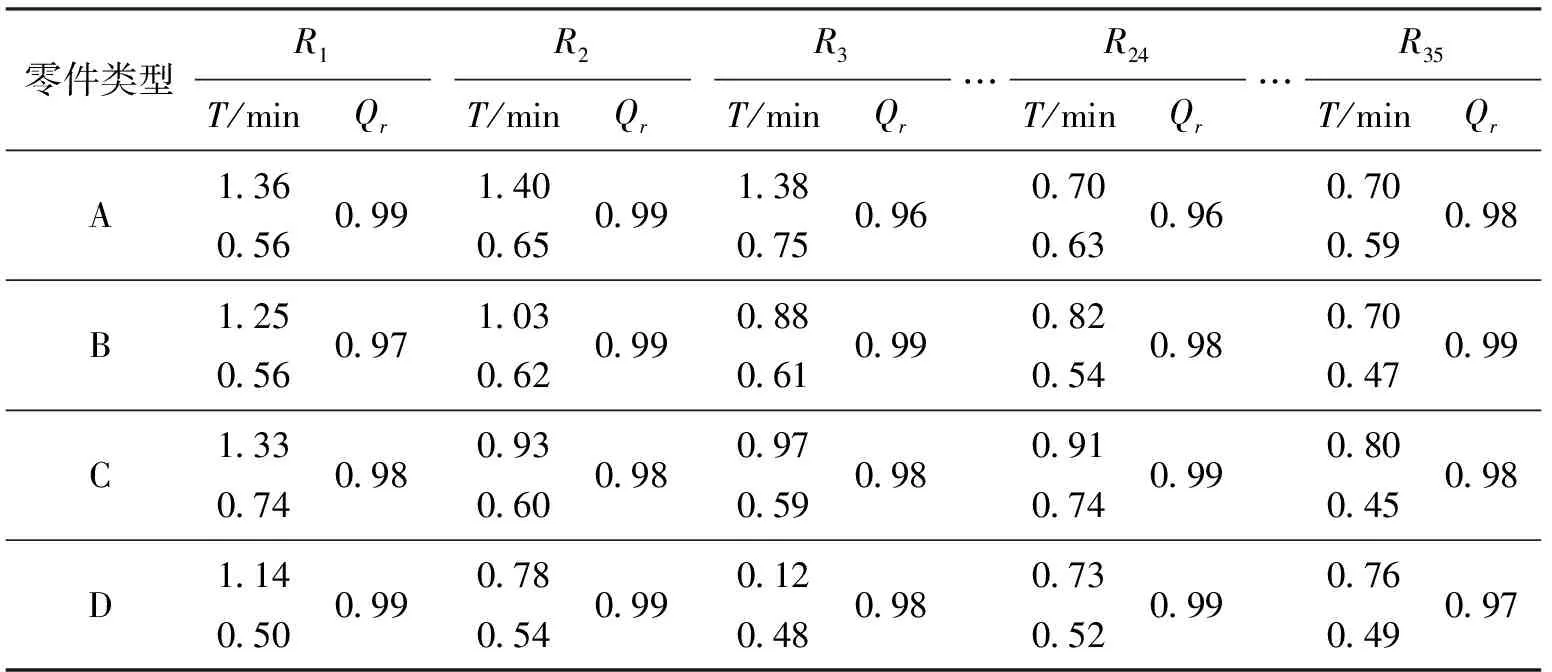
表1 零件标准处理时间、准备时间及节点服务能力

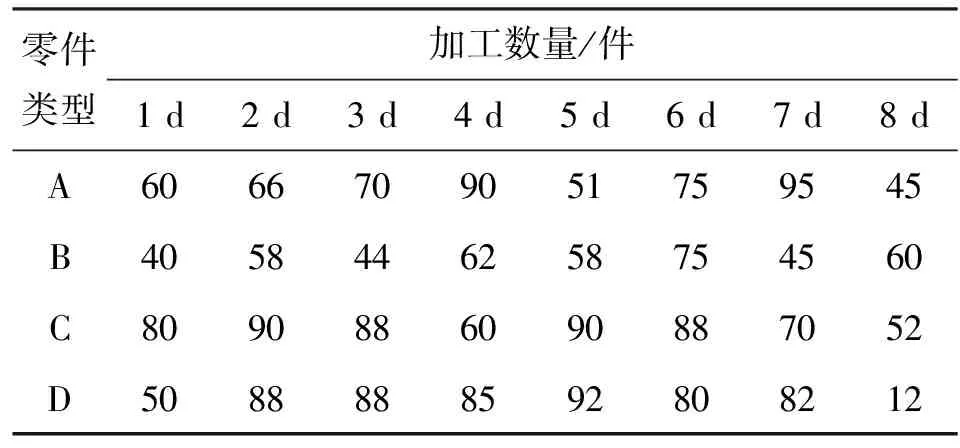
表2 每天加工的零件数量

4.2 模型的建立

由于所采集数据集均为A车间生产计划和MES系统的原始数据,需经过一定转化,转化后的车间数据集制造网络模型如图3所示。图中示出了A车间制造网络演化后的最大连通子图,同时该车间系统网络模型也从微观结构揭示了该车间内部高度互联的作业结构。

4.3 瓶颈预测

(1)正常工况下瓶颈的监测。根据该车间MES系统真实反馈数据和实际观测情况,确定各节点在观察期内的瓶颈状态,如表3所示。

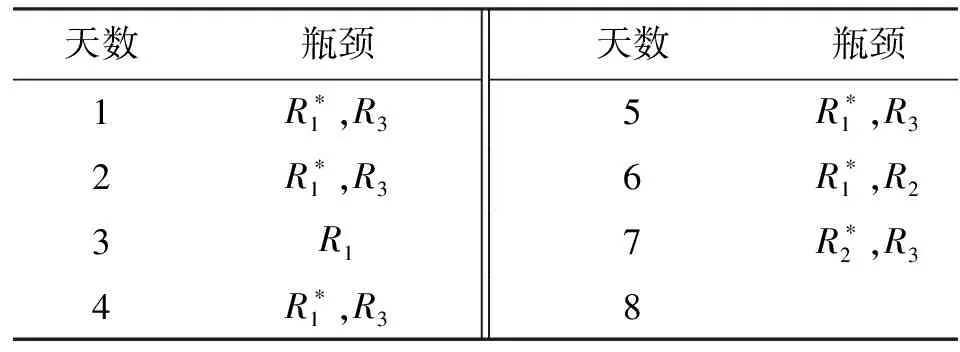
表3 观测期间车间实际瓶颈

注:*表示多瓶颈存在时,该瓶颈为主瓶颈。

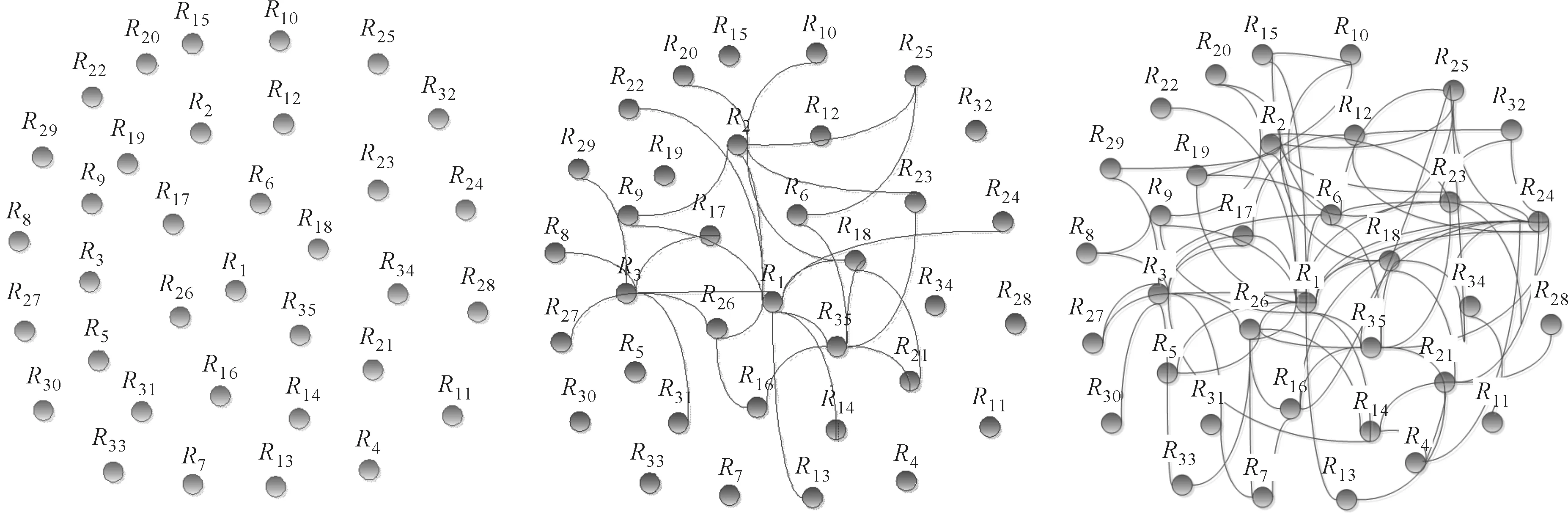
(a)初始网络 (b)演化网络 (c)演化后最大连通示图图3 A车间网络拓扑结构

(2)扰动环境下瓶颈的预测。采用基于改进CML模型的瓶颈度计算方法,预测该机电产品企业A作业车间在扰动环境下工作站瓶颈度的变化情况。为验证方法的准确性,利用Arena仿真软件对该组实验数据进行同步验证,以对结果做一比对。各工作站的工件排队时间和排队数量可反映节点瓶颈状态预测的合理性。

扰动因素F1:订单交货期变更。在预测的第2天,根据客户需求,订单2015071308交货期提前,因此在原有计划的基础上加入B产品50件。根据式(6)可得扰动因素F1的扰动类型为强相关扰动。

扰动因素F2:紧急插单。在预测的第4天,紧急订单2015071396到达,该扰动使得在原有计划的基础上加入新产品E,工艺路线为Oij=(R23,R3,R5),计划产量为60件。根据式(7)可得扰动因素F2的扰动类型为弱相关扰动。

利用CML瓶颈度计算模型,以1 h为仿真步长,计算仿真周期64 h内各工作站瓶颈度的变化情况,结果如表4所示。

表4 节点瓶颈度计算(8 d)

(3)扰动环境下Arena仿真验证。利用Arena仿真软件对该工作车间扰动环境下的工况进行建模仿真,采用每个工作站的仿真队列长度来表明该节点的瓶颈程度。即等待使用该工作站的工件排队时间越长,排队数量越多,则该工作站成为瓶颈的可能性就越大,仿真结果如表5所示。其中,工作站R1的平均排队等待时间为16.34 min,平均工件等待个数为9.98;工作站R3的平均排队等待时间为13.07 min,平均工件等待个数为12.80,均居于所观测工作站前列,这表明工作站R1、R3最有可能成为系统瓶颈。仿真结果与CML模型的预测结果具有较好的一致性,故此证明了算法的正确性与有效性。

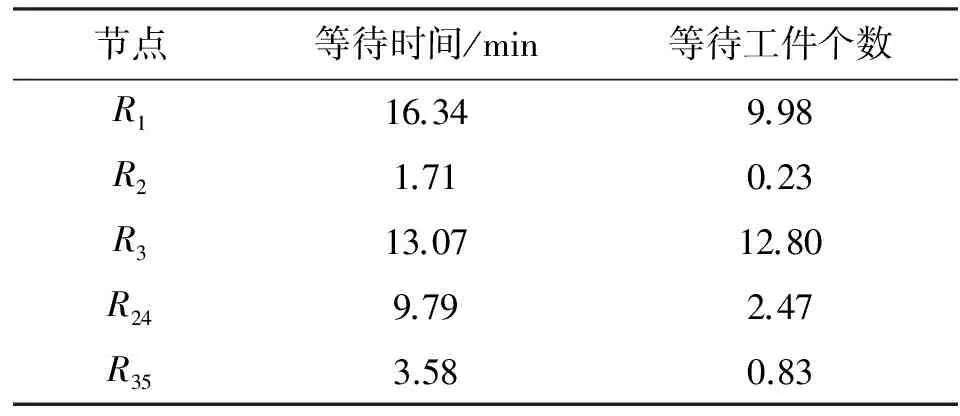
表5 Arena仿真队列明细表

4.4 数据分析

为深入进行数据分析:①比较同一工作站在不同时间段内瓶颈度的变化,进行特定工作站瓶颈波动特性分析;②比较同一时段内不同工作站瓶颈度的大小,完成瓶颈漂移的可视化。

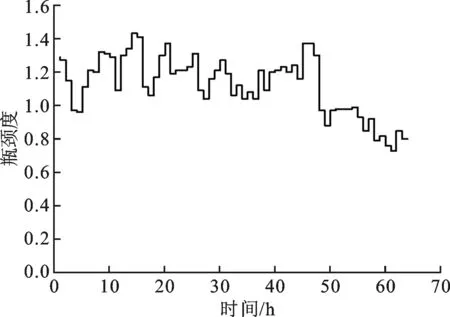
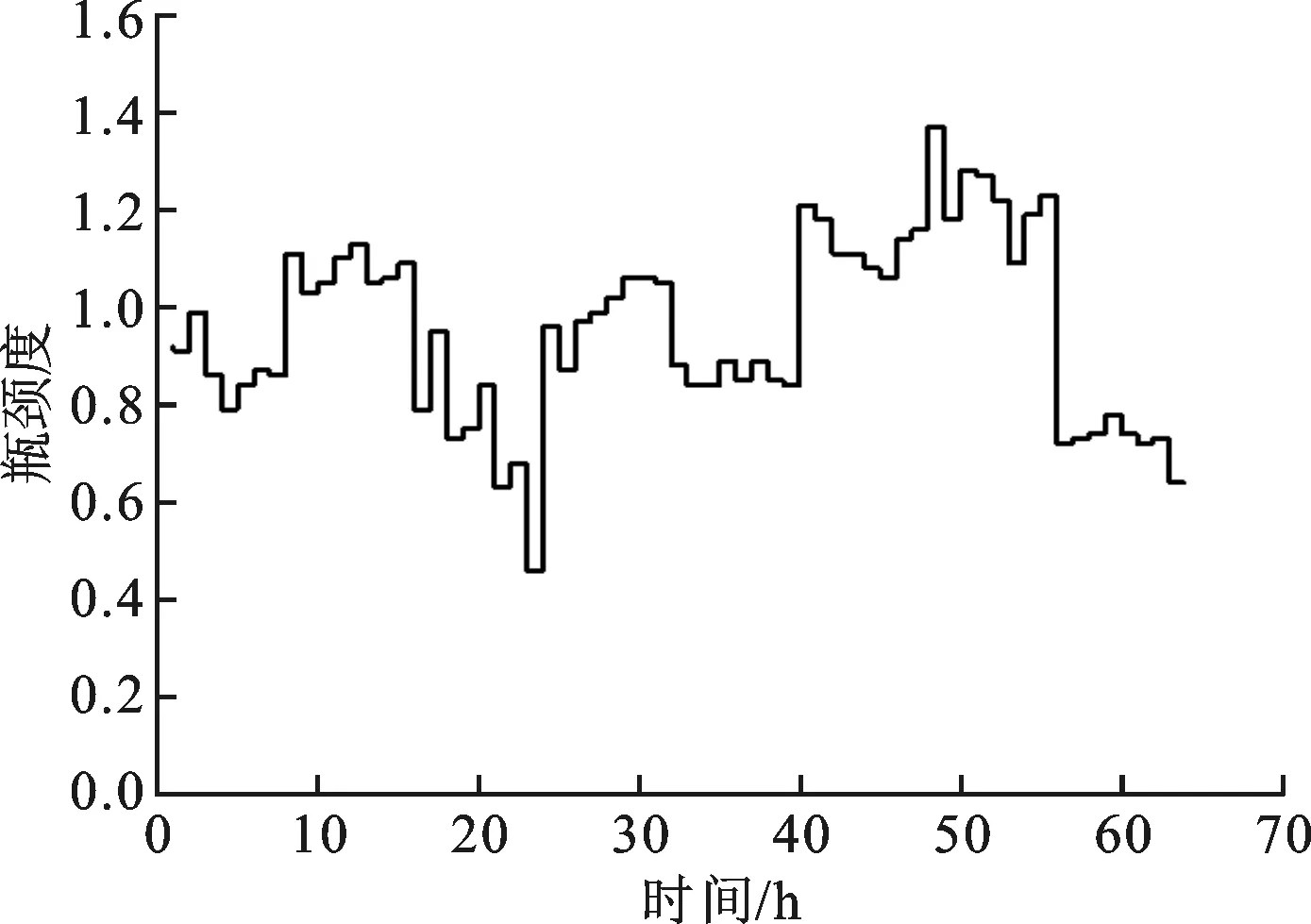
(a)R1

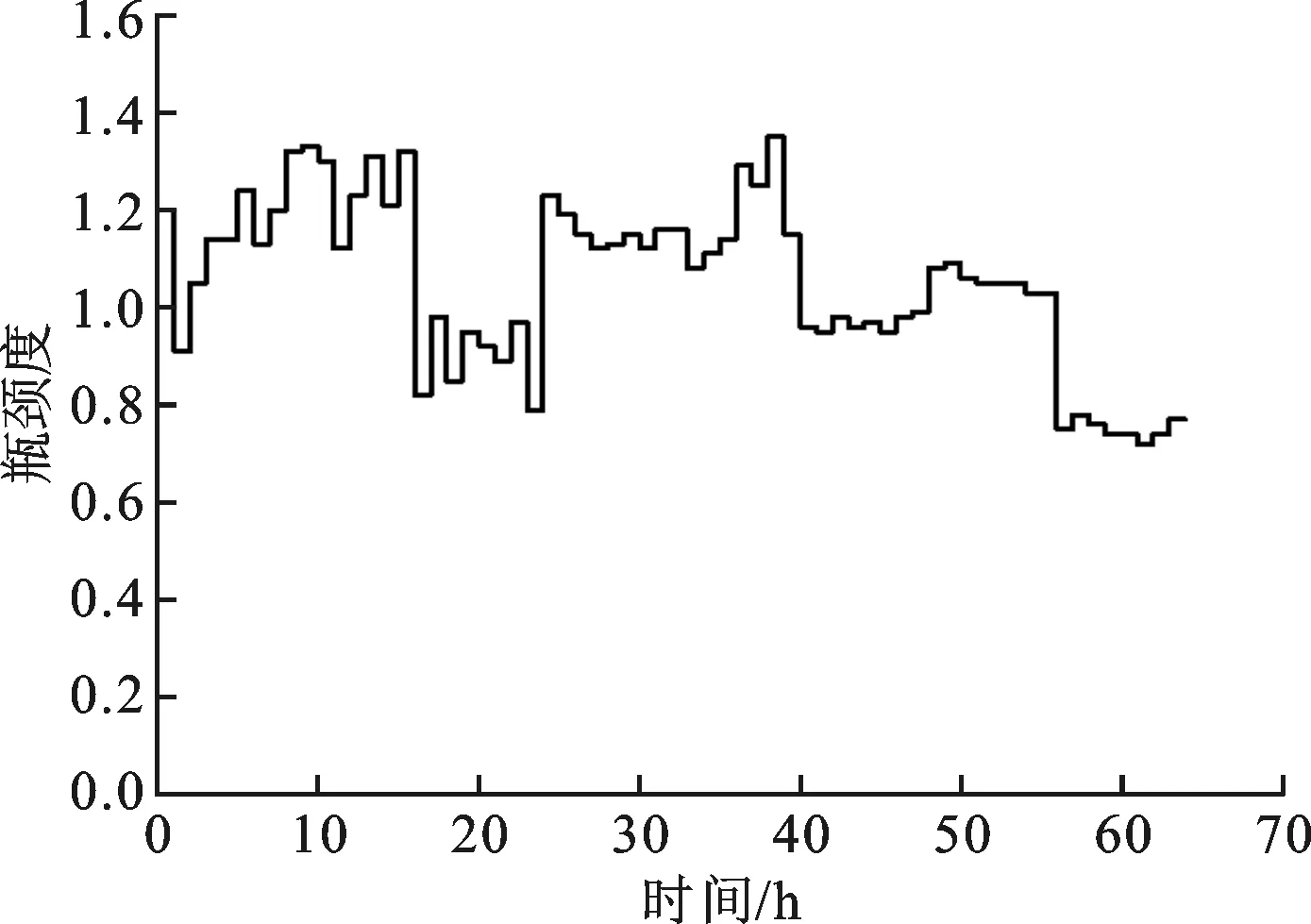
(b)R2

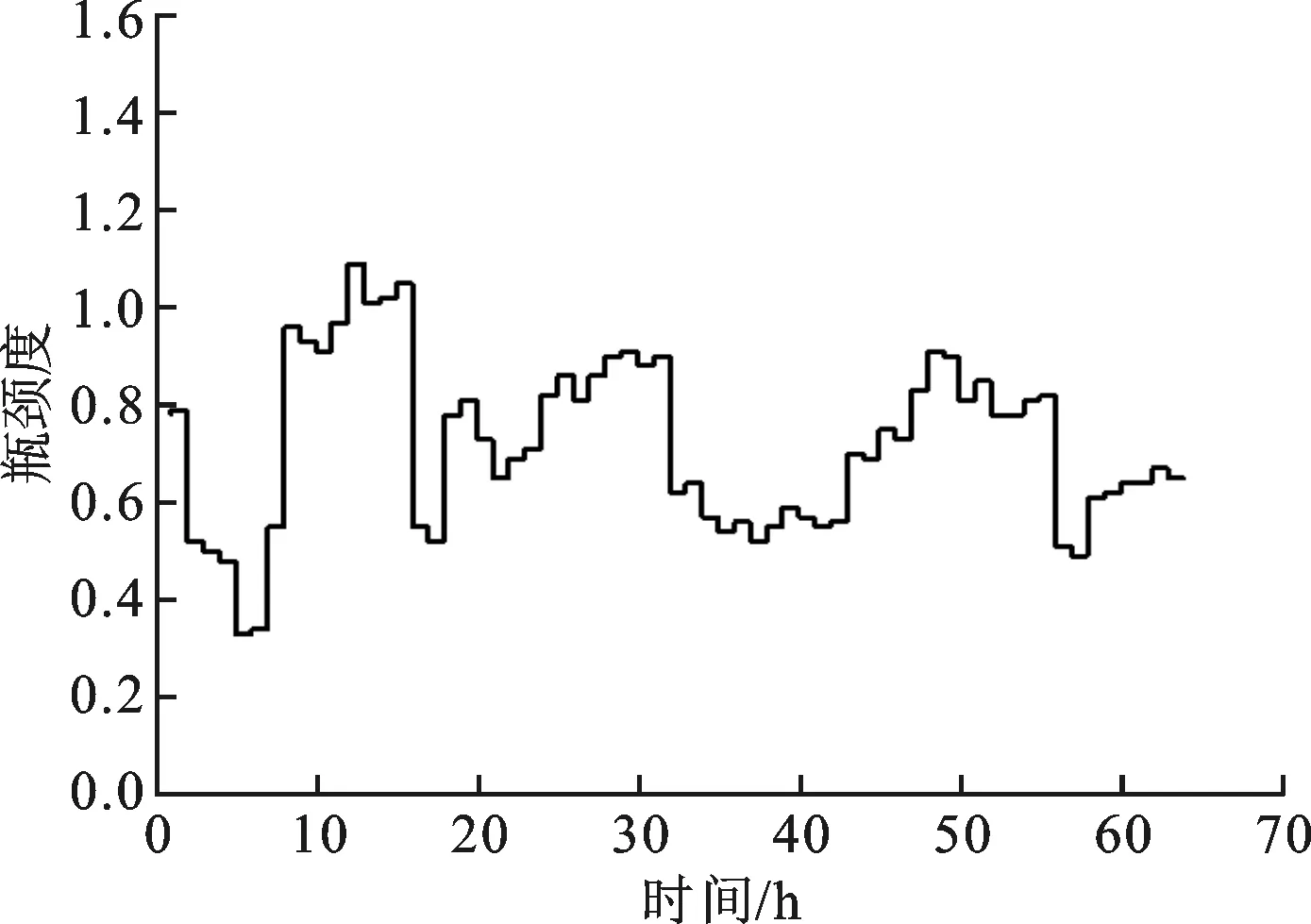
(c)R3

(d)R24

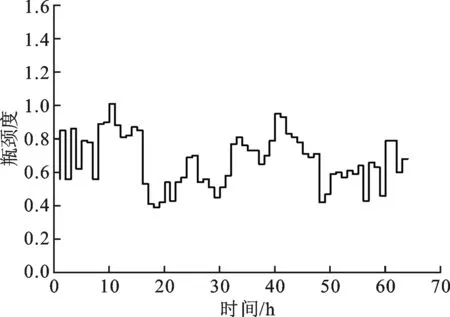
(e)R35图4 节点瓶颈波动特性分析

(1)瓶颈度波动特性分析。计算得到各工作站瓶颈度如图4所示。其中,工作站R1瓶颈度的值域为[1.43,0.73],平均值为1.12,在所有工作站中处于较高水平;其次是工作站R3,值域为[1.21,0.72],平均值为1.05。各工作站平均瓶颈度为0.75。由此可见,工作站R1与R3最有可能成为系统的主瓶颈。此外,工作站R1和工作站R24的瓶颈度波动幅度较大,标准偏差分别为0.17和0.19。该数据表明二者在有效产出时间内的稳定性较差。瓶颈度的波动性越不稳定,说明该工作站对系统中的扰动因素越敏感,需要采取一定的手段进行有效控制和预防。

(2)瓶颈漂移可视化。通过模型计算,可以得出8个工作日内各工作站在任一时段瓶颈度的变化情况,以及系统瓶颈工作站的变化规律,如图5所示。其中,阶梯图可反映瓶颈在不同工作站之间的漂移情况,以及该工作站持续成为瓶颈的时间;火柴梗图可反映当某工作站成为瓶颈时,其瓶颈度的大小。在该作业车间系统中,工作站R1、R3首先成为系统的瓶颈;随着加工进度的推移,R1和R24两个工作站交替成为系统瓶颈,但工作站R1占据系统瓶颈的时间长达40 h。在实际生产环境中,R1为车间干燥管资源,R3为电子开料锯资源,R24为热压机资源。此结果与实际车间情况相吻合,在资源有限的情况下,热压机、电子开料锯、绝缘加工中心为车间的关键设备,而干燥管则为车间的瓶颈设备。

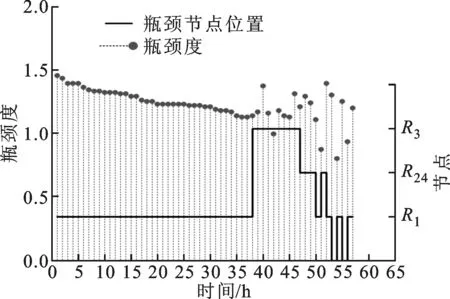
图5 瓶颈节点变化及其瓶颈度值

综上可见,通过对瓶颈漂移及其持续时间的分析,有助于寻找影响系统性能的关键工作站;此外,对瓶颈工作站瓶颈度变化规律进行分析,可以帮助车间管理层深入发掘瓶颈形成的真正缘由,实现瓶颈改善、成本的量化计算,为决策者确定采取何种改善措施实现系统性能的优化提供依据。

5 结 论

(1)从复杂网络视角出发,对作业车间进行复杂生产网络建模和分析,在理论上揭示作业车间系统各构成要素及其相互作用关系。综合考虑扰动在生产网络中的传播机制以及对其他节点的影响机理,建立了基于CML的瓶颈识别算法。在保证瓶颈预测精度的前提下,实现了作业车间瓶颈的量化描述和连续预测。

(2)为专注于研究扰动因素的传播对制造系统瓶颈与性能的影响,本文做出了一定的假设,如不考虑设备停工与维修等不确定因素的影响。在后续研究中,可以综合考虑多重不确定因素的影响,分析系统瓶颈的动态变化规律。此外,提前预知瓶颈工位及其转移趋势,实现瓶颈的事前控制,能使管理者更好地应对瓶颈,这也是下一步研究的重点。

[1] ROSER C, NAKANO M, TANAK M. Comparison of bottleneck detection methods for ACV systems [C]∥Proceedings of the 2003 Winter Simulation Conference. Piscataway, NJ, USA: IEEE, 2003: 1192-1198.

[2] LI Lin. Bottleneck detection of complex manufacturing systems using a data-driven method [J]. International Journal of Production Research, 2009, 47(24): 6929-6940.

[3] KASEMSET C, KACHITVICHYANUKUL V. Simulation based procedure for bottleneck identification [C]∥Proceedings of Communications in Computer and Information Science. Berlin, Germany: Springer-Verlag B, 2007: 43-59.

[4] 王军强, 康永, 陈剑, 等. 作业车间瓶颈簇识别方法 [J]. 计算机集成制造系统, 2013, 19(3): 540-547. WANG Junqiang, KANG Yong, CHEN Jian, et al. Identification approach for bottleneck cluster in a job shop [J]. Computer Integrated Manufacturing System, 2013, 19(3): 540-547.

[5] 翟颖妮, 孙树栋, 王军强, 等. 大规模作业车间的瓶颈分解调度算法 [J]. 计算机集成制造系统, 2011, 17(4): 827-831. ZHAI Yingni, SUN Shudong, WANG Junqiang, et al. Scheduling algorithm based on bottleneck operations decomposition for large-scale job shop scheduling problems [J]. Computer Integrated Manufacturing System, 2011, 17(4): 827-831.

[6] 凌琳, 刘明周, 王强. 物料流瓶颈对制造车间不确定环境的敏感性研究 [J]. 农业机械学报, 2013, 44(2): 224-232. LING Lin, LIU Mingzhou, WANG Qiang. Sensitivity of material-flow bottleneck to uncertain environment in job shop [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(2): 224-232.

[7] LIU Mingzhou, TANG Juan, GE Maogen, et al. Dynamic prediction method of production logistics bottleneck based on bottleneck index [J]. Chinese Journal of Mechanical Engineering, 2009, 22(5): 710-716.

[8] JIANG Hongquan, GAO Jianmin, CHEN Fumin. System failure analysis based on complex network theory [C]∥Annual Reliability and Maintainability Symposium. Piscataway, NJ, USA: IEEE, 2009: 176-181.

[11]TILL B, MIRJA M, KATJA W. A manufacturing system network model for the evaluation of complex manufacturing system [J]. International Journal of Productivity and Performance Management, 2014, 63(3): 324-340.

[12]SCHOLZ-REITER B, WINTD K, LIU H. Modelling dynamic bottleneck in product network [J]. International Journal of Computer Integrated Manufacturing, 2010, 24(5): 391-404.

[13]刘夫云, 杨清海, 祁国宁. 基于复杂网络的产品族零部件通用性分析方法 [J]. 机械工程学报, 2005, 41(11): 75-79. LIU Fuyun, YANG Qinghai, QI Guoning, et al. Universality analysis method of parts for product family based on complex network [J]. Journal of Mechanical Engineering, 2005, 41(11): 75-79.

[14]李晓娟, 袁逸萍, 孙文磊. 基于网络结构特征的作业车间瓶颈识别方法 [J]. 计算机集成制造系统, 2016, 22(4): 1089-1096. LI Xiaojuan, YUAN Yiping, SUN Wenlei, et al. Research of bottleneck identification in job-shop based on network structure characteristic [J]. Computer Integrated Manufacturing System, 2016, 22(4): 1089-1096.

[15]李晓娟. 复杂产品制造过程加权演化模型与节点重要度分析 [M]. 乌鲁木齐: 新疆大学, 2012: 30-44.

[16]KANEKO K. Coupled map lattices [M]. Singapore: World Scientific, 1992: 52-77.

(编辑 杜秀杰)

Multi-Bottleneck Identification for Job-Shop Network in Disturbance Environment

LI Xiaojuan,SUN Wenlei,YUAN Yiping,LI Huahua

(School of Mechanical Engineering, Xinjiang University, Urumq 830047, China)

Aiming at the issues that the bottleneck identification is difficult and the bottleneck identification is not global and effective after bottleneck drift for job-shop network in disturbance environment, a new web-based manufacturing multi-bottleneck identification method is presented. A network model of job-shop is established according to multiple levels of production data, such as equipment and tooling, process route, logistics path, product configuration, etc. The kinetic equations of job-shop network are established, and the criterion of transfer of disturbance factors is thus obtained. Expending bottleneck connotation, a bottleneck identification strategy is proposed based on CML method. By comprehensively considering the characteristics of dynamic node itself, network topological structure and propagation mechanism of disturbance in the network, continuous quantitative description and prediction of job-shop bottlenecks are realized. An example for dynamically monitoring and forecasting the bottleneck in a job shop verifies the validation and practicability of the proposed method. The results show that in disturbance environment, CML model can better predict the trend of the bottleneck degree of the workstations. The average bottleneck degree of workstationR1is 1.12 and the bottleneck lasts for 40 h, and the average bottleneck degree of workstationR3is 1.05 and the bottleneck lasts for 10 h. WorkstationsR1andR3become the first bottleneck of the system, along with the progress of the process workstationsR1andR24alternately become the system bottleneck.

job shop; disturbance environment; complex network; CML method; bottleneck identification

2016-05-11。 作者简介:李晓娟(1987—),女,讲师,博士生;孙文磊(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51365054,51565055);新疆维吾尔自治区自然科学基金资助项目(2014211A008)。

时间:2016-09-23

10.7652/xjtuxb201612011

TH166;TP181

A

0253-987X(2016)12-0064-09

网络出版地址:http: ∥www.cnki.net/kcms/detail/61.1069.T.20160923.1711.018.html