用于柔性转子主动控制的等几何Timoshenko梁模型及其数值验证
2016-12-22张鹏飞王志恒席光
张鹏飞,王志恒,席光
(西安交通大学能源与动力工程学院,710049,西安)
用于柔性转子主动控制的等几何Timoshenko梁模型及其数值验证
张鹏飞,王志恒,席光
(西安交通大学能源与动力工程学院,710049,西安)
为了克服采用标准有限元方法建立的转子模型自由度多不便直接用于控制器设计的问题,结合等几何分析方法的精度高、自由度少的特点,提出了把低阶等几何Timoshenko梁模型运用到柔性转子的主动控制中,并进行了数值验证。首先,给出了半离散等几何模型及在主动控制中作为转子控制输入信号的各类边界条件;其次,分别对比了高、低阶等几何模型的奇异值响应以及简支条件下的高、低阶模型的数值解与理论解;最后,在采用磁悬浮轴承支撑和给定分布不平衡力扰动的条件下,对转子进行了分散比例微分(PD)仿真控制。结果表明:所采用的低阶模型的奇异值响应在前6阶临界转速范围内与高阶模型基本一致;高阶模型的前10阶模态频率很好地吻合了理论解,低阶模型前4阶模态频率误差在0.2%以内;高、低阶等几何梁模型下的转子不平衡振动位移稳态响应的差别很小,该误差可看成工作转速下的同频小扰动。低阶等几何梁模型在低频范围的高精度验证了该方法所得低阶模型直接用于控制器设计的可行性。
等几何方法;柔性转子模型;Timoshenko梁;振动控制;磁悬浮轴承
在航空、电力、石化等领域,各类旋转机械都向着高速、高功重比方向发展,为了限制转子的重量和线速度,减小离心力,高速转子往往采用细长型的柔性转子,工作转速通常高于其一阶、二阶临界转速,甚至达到三、四阶临界转速以上[1]。主动磁悬浮轴承的高速、无磨损、无润滑及可控性等优点使其成为高速转子支承的理想方案[2]。主动磁悬浮轴承支撑的转子控制方法主要基于数学模型,虽然许多先进算法(如鲁棒控制、滑模控制等)可以降低对转子建模精度的敏感性,但转子的建模精度还是会直接影响其控制性能。
大量实践表明,5自由度刚性转子简单、有效,可直接用于主动磁悬浮轴承的刚性转子控制[3-5]。对于柔性转子,其主动控制要求建立更精确的转子模型,采用标准有限元方法对柔性转子进行建模和分析已经比较成熟,且有限元方法相比传递矩阵法更加精确[6]。但是,有限元方法所得模型自由度数目较大,不便于直接用于控制器的设计,尤其当控制器设计的复杂程度依赖于转子的数学模型时,例如鲁棒控制。用于这类控制器的柔性转子模型通常先采用标准有限元方法或集总参数法建立高阶转子模型,模型经过修正后,利用子结构技术(例如Guyan、Hurty模态截断等方法)或状态空间技术对高阶转子进行简化[7]。
标准有限元方法、子结构技术和状态空间方法已经较为成熟,但由于有限元方法求解自由振动问题所得频率谱的不连续性[12],基于有限元法的子结构技术要求其所建模型具有较多的自由度数目,否则难以保证模型的精度。状态空间方法仍然缺乏处理大规模系统的能力,需要采用子结构技术先进行一次降阶[2]。
等几何方法[8]是一种基于非均有理B样条基函数的数值方法,主要实现了几何模型与分析模型的一致表达,已经广泛应用于工程问题的优化,结构的强度、振动分析[9],流体分析[10-11]和电磁分析等领域。在转子动力学领域,文献[12]研究了欧拉-伯努利梁的自由振动,与有限元方法对比,说明等几何方法精度高,且其频率谱连续;文献[13]分析了Timoshenko梁的自由振动,成功避免了振动分析中剪切自锁现象;文献[14]分析了各类边界条件下方形Timoshenko梁的自由振动,发现网格k细分方法得到的结果最好,即在较少单元数目和基函数阶次下可得到更高精度;文献[15]提出了一种超收敛等几何方法,并用于欧拉梁的振动问题;文献[16]采用等几何方法建立非线性几何欧拉梁模型。
由于等几何方法具有得到精度高且阶数低的梁模型特性,本文提出采用等几何方法获得低阶Timoshenko转子模型以替代由有限元模型并进行模型缩减后所得模型,由此可以把低阶等几何Timoshenko转子模型直接用于柔性转子的控制器设计。所得模型可以根据需要实时调整物理参数,特别是像转子转速等实时变化的物理参数。数值分析中的边界条件对应于控制领域中的输入信号,为了能使其在主动控制中运用,本文将各类主动控制中可能用到的边界条件进行了整理和推导,并将数值解与理论解进行对比,验证所建模型的正确性。最后,进行了在高、低阶等几何Timoshenko梁模型下的奇异值响应分析,并采用磁悬浮轴承支撑转子,考虑分布质量不平衡,分别进行了分散PD控制仿真,通过对比仿真结果,初步验证该模型用于主动控制的可行性。
1 等几何Timoshenko梁建模
1.1 微分方程
假设梁微小变形且不考虑扭转变形、轴向变形的前提下,对于变截面均质对称圆形截面Timoshenko梁-轴,不失一般性,令其中性轴位于z轴,且z∈(0,L),控制方程的微分形式[16]如下
(1)
式中:ux(z,t)、uy(z,t)为中性轴横向位移分布;φx(z,t)、φy(z,t)为截面转角分布;fx(z,t)、fy(z,t)为分布载荷力;mx(z,t)、my(z,t)为分布载荷力矩;A(z)为横断截面面积;Ix(z)、Iy(z)为截面惯性矩;Ip(z)为极惯性矩;ρ为材料的密度;E为材料的弹性模量;G为材料的剪切模量;μ为梁的剪切修正系数;Ω为转子工作转速;L为转子长度。
1.2 半离散等几何Timoshenko梁模型
与标准有限元相比,等几何单元采用非均有理B样条基函数作为插值基函数,本文采用B样条作为等几何单元的插值基函数。式(1)的变分形式可直接采用伽辽金(Galerkin)方法推导得到。本文在采用等几何方法时,仅对空间进行离散,保持时间域连续,可得到半离散动力学模型。由于篇幅所限,关于等几何方法的详细介绍可以参考文献[9],这里仅列出最后的半离散模型

(2)
式中:M、G、K分别为4n×4n总质量矩阵、总陀螺矩阵和总刚度矩阵;F为4n×1广义力向量矩阵。
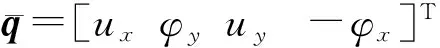
(3)
式中:W=diag(n(ξ),n(ξ),n(ξ),n(ξ)),n(ξ)为p次B样条的n个基函数组成的假设模态列向量,可表示为
其中B样条基函数Ni,p(ξ)的定义方法可参考文献[18]。本文采用k型网格细分方法[14],等几何单元数目ne、基函数数目n以及基函数阶次p满足以下关系式n=ne+p。
2 边界条件处理
为了便于将等几何梁模型用于柔性转子的主动振动控制,本文整理和推导了在振动控制、分析方面可能用到的边界条件。边界条件主要考虑了齐次边界条件,包括简支、固持、导向、自由、拉伸弹簧、抗弯弹簧等6种边界条件,还有转子上的集中广义力、集中广义质量单元、弹簧阻尼单元以及不平衡分布质量引起的不平衡力非齐次边界条件。
2.1 齐次边界条件
齐次边界条件是几何、力边界条件的组合,如表1所示。位移和转角边界条件对应于有限元中的第一类边界条件(Dirichlet边界条件),力矩边界条件对应第二类边界条件(Neumann边界条件),力边界条件为第三类边界条件(Robin边界条件),它们的处理方法与有限元方法相同。在表1中,k为拉伸弹簧刚度,κ为抗弯弹簧刚度,zp为边界条件位置,特别地,在转子两端,zp=0,L。

表1 齐次边界条件
2.2 集中的广义力、质量及弹簧阻尼单元
集中广义力是转子振动控制的输入,首先给出作用梁上在任意位置下径向广义力表达式。根据集中广义力的位置,可以分为3种情形:①转子两端点处;②等几何单元两端点处;③等几何单元两端点间。经过推导,等几何坐标下任意位置的广义力F都可以表示成
(4)

(5)

梁上的集中质量、惯量可以做为外力引入到力学模型中去,结合式(5)有
(6)
式中

(7)
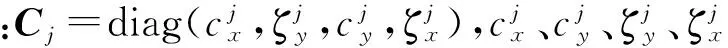
将式(6)、式(7)代入式(5),分别有
(8)
(9)

2.3 分布不平衡力
分布不平衡力由不平衡质量引起。假设质量偏心的幅值沿轴向分布为e(z),初始相位为0,则转速恒定条件下分布不平衡力为
(10)
根据式(4),对式(10)积分,则有
(11)
则由分布不平衡质量引起的不平衡力矩阵为
3 算例验证
以下从两个方面来验证等几何建模方法所得到的转子模型用于柔性转子控制的可行性:一是通过奇异值分析对比低阶模型与高阶模型的差异,并且在简支条件下进行模型对比验证;二是假设Timoshenko转子采用电磁轴承支撑,考虑转子的分布质量不平衡,将所得的低阶、高阶等几何Timoshenko转子模型与电磁轴承力学模型一起采用PD控制算法进行控制仿真,并比较两者差异。
3.1 状态空间模型及转子参数
令
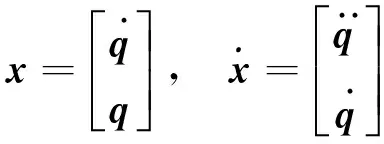
结合式(3)、式(5),得到式(2)的状态空间方程
(12)
式中
式(12)通过拉普拉斯变换得到系统的传递函数
G(s)=C(sI-A)-1B
(13)
本文所采用的Timoshenko转子主要参数见表2。
3.2 奇异值分析
奇异值分析可以得到系统传递函数随频率变化的奇异值响应。给定传递函数的奇异值具有唯一性,因此可用来刻画系统降阶前后输入、输出响应的逼近程度。先将s=jω代入所得传递函数矩阵式(13),再进行奇异值分解可得到奇异值响应函数。

表2 Timoshenko转子参数
注:带有“#”的参数由不带“#”的参数计算得到。
Timoshenko转子两端在x、y方向上都有拉伸弹簧以及拉伸阻尼器,且输入广义力的位置以及广义位移观测位置也都在转子两端。拉伸弹簧刚度系数为2×106N/m、拉伸阻尼器阻尼系数为1×103kg/s,其他参数见表2。使用的等几何单元数量ne分别为2和32,B样条基函数阶次p=8。该转子系统的奇异值响应函数曲线如图1所示。

图1 高阶、低阶转子系统传递函数的奇异值响应
从图1中可以看出,当等几何单元数目取为32和2、基函数阶次取为8时,即式(2)的阶数分别为160和40,系统传递函数的奇异值响应在频率小于3 000 rad/s范围内差异很小。采用等几何方法对该模型进行有阻尼模态分析(ne=32,p=8),可得到Campbell图,从而得到转子前6阶临界转速,分别为123.76、418.40、736.40、1 110.2、1 748.7、2 722.5 rads-1。3 000 rad/s已超过转子系统的第6阶临界转速,所以研究前几个低阶模态频率范围内的问题时,直接使用等几何Timoshenko转子模型作为控制模型是可行的。
3.3 模型验证
通过对比转子模态频率的数值解与理论解,以验证所建立等几何Timoshenko梁模型的准确性,采用模型参数如表1所示,边界条件为两端简支。
等截面Timoshenko梁在两端简支条件下无量纲ω*模态频率满足下式[17]
(14)
式中
i∈N*;ω0=(π/L)2(EIy/(ρA))1/2
ω*=ω/ω0;Ω*=Ω/ω0
由式(2)、式(14)可分别得到无量纲模态频率的数值解(ne=32,p=8)和理论解,其中前10阶前向无量纲模态频率如表3所示,两者相对误差绝对值最大为1.52×10-11。表4为高、低阶等几何Timoshenko梁模型的前6阶前向无量纲模态频率的数值解比较,前4阶误差在0.2%以内,但第5、6阶相对误差分别达到了6.42%与10.8%。可见,低阶等几何Timoshenko模型的准确性在前4阶弯曲模态频率范围内的精度可以保证。若要求得更高的控制精度,则应通过模态截断等方法获得更高精度的低阶等几何Timoshenko模型。

表3 前10阶无量纲前向模态频率的数值解与理论解
注:加粗数值为2种解的不同部分。
3.4 理想PD控制仿真
Timoshenko转子采用一对相同的主动径向磁悬浮轴承(AMB)支撑Timoshenko转子,磁悬浮轴承采用分散重合PID控制,即每个磁悬浮轴承的x、

表4 高、低阶模型无量纲前向模态频率的
y方向的电磁力都用单通道PID控制,共4个通道。为方便考察高、低Timoshenko梁模型在相同控制下的差异,本文不考虑非并置问题和重力效应,采用可行的最简单控制方法,作出如下设置:①传感器轴向位置与磁悬浮位置相同,都在转子两端;②不考虑转子重力影响;③PID控制采用最简单的理想PD控制器。磁悬浮系统的控制原理如图2所示。磁悬浮轴承的电磁力采用线性化模型
Fx=-Ksx+Kiix;Fy=-Ksy+Kiiy
(15)
式中:位移刚度Ks=-2 MN/m;电流刚度Ki=250 N/A。

图2 磁悬浮轴承-转子系统反馈控制框图
假设简化的功率放大器、传感器传递函数为
P(s)=KPA;S(s)=Ksen
(16)
式中:功率放大器直流增益KPA=1 A·V-1;位移传感器直流增益Ksen=7 800 V/m。
采用的理想PD控制器
C(s)=KP+KDs
(17)
式中:比例放大系数KP=2.051 3;微分系数KD=5.128 2×10-4。
比例放大系数KP使得磁轴承的等效刚度为K=2 MN/m,而微分系数KD使得磁轴承的等效阻尼为C=1 000 kg/s,此时磁悬浮轴承仍可看成拉伸弹簧-阻尼组合单元。
假设转子有恒定工作转速Ω,亚临界转速取第一阶临界转速的一半,超临界转速分别取相邻临界转速的算术平均值,如表5所示。
以分布不平衡质量引起的不平衡力作为扰动源,假设式(10)中的x、y方向上的偏心沿z轴分布ex(z)、ey(z)分别为
(18)

(a)Ω=61.880 rad/s
(b)Ω=271.080 rad/s
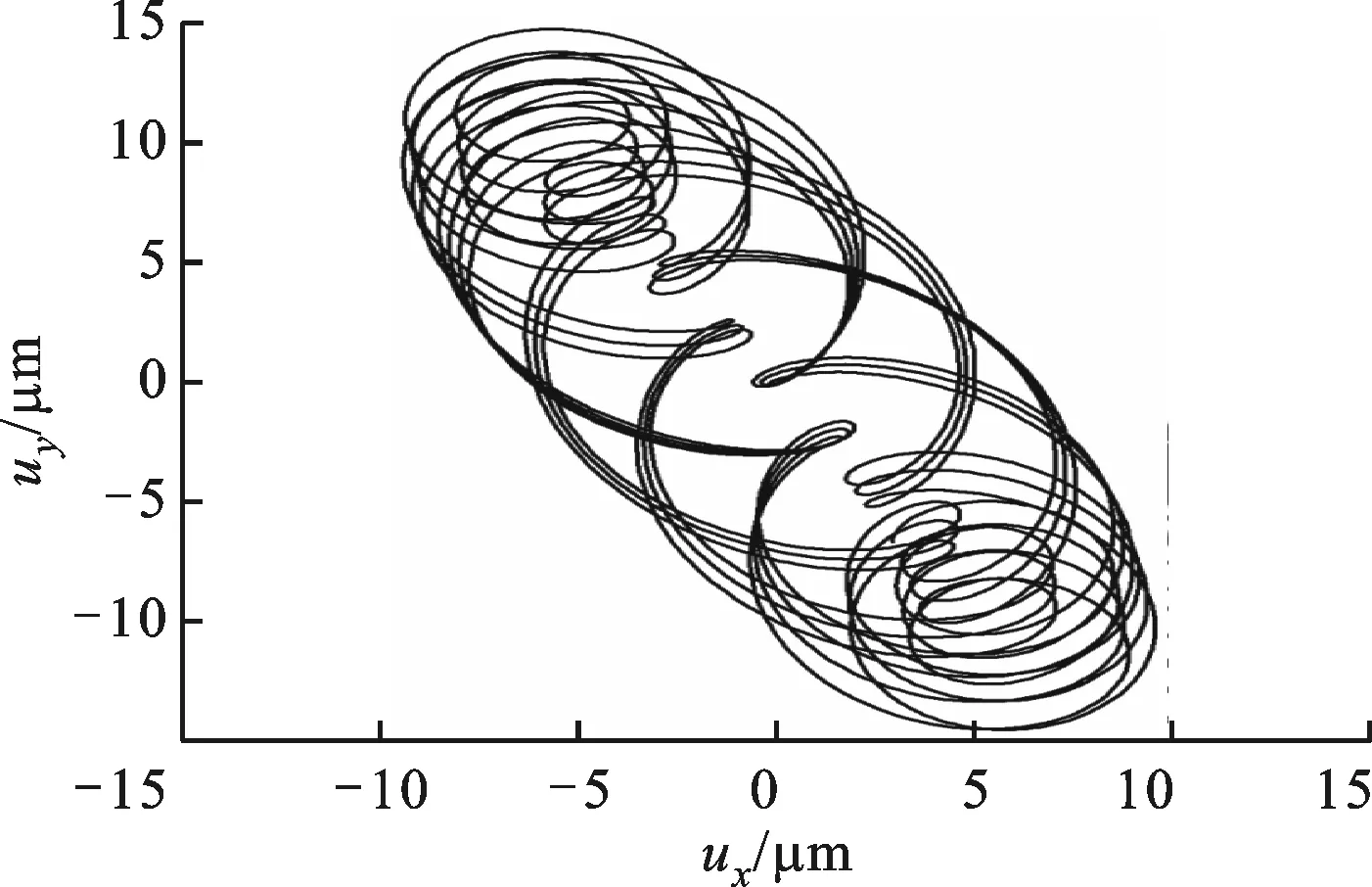
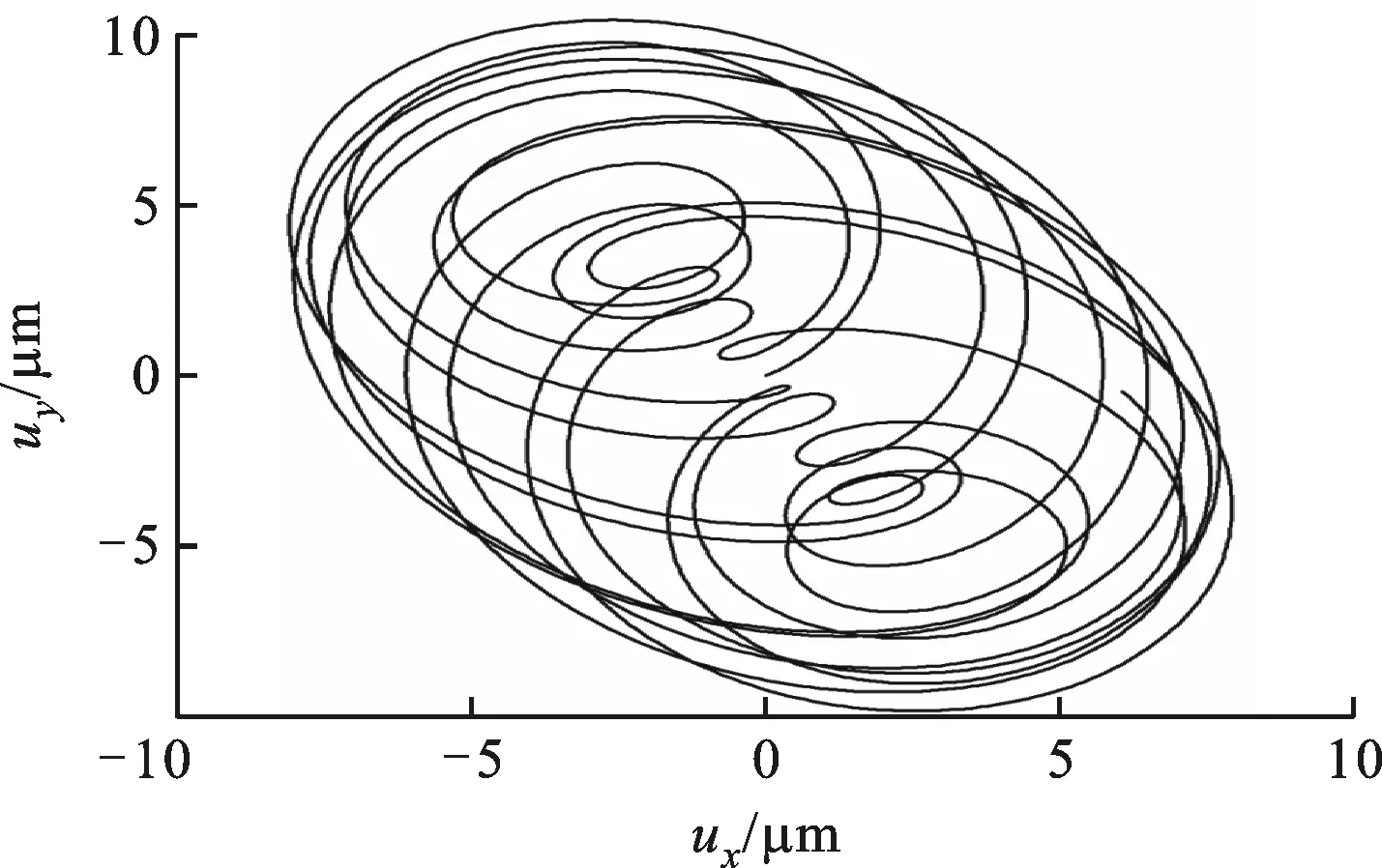
(c)Ω=577.265 rad/s图3 高阶转子模型0.5 s内不同转速下转子跨中横截面形心轨迹
以式(17)的PD算法作为磁悬浮轴承的控制策略,假设在转子初始位移、速度均为0的条件下,分别以高、低阶等几何Timoshenko梁模型作为被控对象,得到了0.5 s内转子跨中截面的形心轨迹以及在x、y轴方向上的位移随时间的响应偏差曲线,其中高阶等几何Timoshenko梁模型对应ne=32、p=8,低阶模型对应于ne=2、p=8。以高阶模型为例,3种不同工作转速下0.5 s内转子跨中截面的形心轨迹如图3所示,ux、uy分别为x、y方向上的位移。从图中可以看出:截面形心轨迹在某一方向上有最大幅值,且随工作转速增加而增大;0.5 s内亚临界工作转速下的幅值最大方向与超临界转速条件下明显不同。
在高、低阶等几何Timoshenko梁模型条件下,转子在3种工作转速时x、y方向上位移响应偏差d曲线见图4。由于采用的模型阶数不同,因此可以反映高、低阶等几何Timoshenko梁模型的偏离程度。如图4所示,除在起始阶段误差曲线呈不规则振动外,后续时刻曲线呈类似周期性波动,波动周期随工作转速增加而减小,后续曲线的最大波动幅值随工作转速增加而增大。6种工作转速下x、y方向上平均波动频率(ω=2π/T,T为平均波动周期)及最大位移波动幅值xm、ym如表5所示,平均波动周期由y方向误差曲线的波峰得到。从表5中可以看出:在误差允许条件下,平均波动频率与转子工作转速相一致,最大相对误差为0.36%;x、y方向的位移波动幅值随工作转速增加而增大,但幅值始终很小。因此,采用低阶等几何Timoshenko梁模型得到的不平衡振动位移稳态响应与高阶模型下的稳态响应偏差很小,在控制中可看成是工作转速下的小扰动。

表5 不同工作转速下位移偏差的波动频率及幅值
由于不平衡质量引起的振动是一种同频的强迫振动,所以稳态位移偏差波动频率与工作转速相近,转子振动的稳态解的频率与强迫振动的频率一致[18],而高、低阶等几何Timoshenko梁模型下的稳态位移偏差相当于同频振动的叠加,所以叠加后其稳态振动频率不变。偏差幅值随工作转速增加而增大,这是因为高、低阶模型偏差总体随工作频率增加而增大。在前6阶临界转速范围内这种偏差很小(可以从图1中反应出来),这是高、低阶模型下,两者的稳态位移偏差很小的原因。
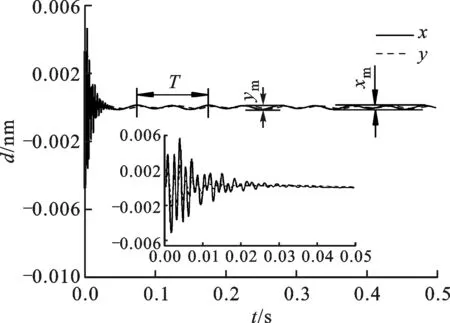
(a)Ω=61.880 rad/s

(b)Ω=271.080 rad/s

(c)Ω=577.265 rad/s图4 高、低阶转子模型下转子跨中形心在x、y方向上的位移偏差
4 结 论
(1)在简支条件下,高阶等几何Timoshenko梁模型在前10阶模态频率范围内具有很高的精度,低阶模型在前4阶模态频率范围内误差较小,最大相对误差小于0.2%。
(2)在前6阶临界转速范围内,低阶等几何Timoshenko梁模型与对应的高阶模型奇异值频率响应基本一致。
(3)在以分布质量不平衡力作为扰动、分散PD算法作为磁悬浮轴承仿真控制策略的条件下,高、低阶等几何Timoshenko梁模型下转子的位移响应频率与工作频率最大相对误差为0.36%,位移波动幅值最大误差在1.9 nm以内,由低阶等几何Timoshenko梁模型引起的误差可看成是工作转速下的同频小扰动。
(4)低阶等几何Timoshenko梁模型在前4阶模态频率范围内能保证模型的精度,该方法所得的低阶模型用于振动控制的可行性得到初步验证,为模型在控制中应用做好铺垫。
[1] 孟光. 转子动力学研究的回顾与展望 [J]. 振动工程学报, 2002, 15(1): 1-2. MENG Guang. Review and prospect of the research on rotor dynamics [J]. Journal of Vibration Engineering, 2002, 15(1): 1-2.
[2] SCHWEITZER G, BLEULER H, MASLEN E H, et al. Magnetic bearings: theory, design, and application to rotating machinery [M]. Berlin, Germany: Springer, 2009: 1-11.
[3] 曹建荣, 虞烈, 谢友柏. 主动磁悬浮轴承的解耦控制 [J]. 西安交通大学学报, 1999, 33(12): 44-48. CAO Jianrong, YU Lie, XIE Youbai. Decoupling control for active magnetic bearing [J]. Journal of Xi’an Jiaotong University, 1999, 33(12): 44-48.
[4] 俞文伯, 栾胜, 房建成. CMG磁悬浮转子系统的模型与控制规律 [J]. 航空学报, 2003, 24(6): 541-545. YU Wenbo, LUAN Sheng, FANG Jiancheng. Model and control strategy of CMG magnetic bearing-rotor system [J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(6): 541-545.
[5] 张剀, 赵雷, 赵鸿宾. 磁轴承飞轮控制系统设计中LQR方法的应用研究 [J]. 机械工程学报, 2004, 40(2): 127-131. ZHANG Kai, ZHAO Lei, ZHAO Hongbin. Study on the application of LQR method in the design of magnetic bearing flywheel control system [J]. Journal of Mechanical Engineering, 2004, 40(2): 127-131.
[6] 方鹏, 蒋科坚. 采用电磁轴承控制柔性转子临界转速分布的建模和仿真分析 [J]. 浙江理工大学学报(自然科学), 2014, 31(3): 221-227. FANG Peng, JIANG Kejian. Modeling and simulation analysis of controlling distribution of critical speed of flexible rotor with electromagnetic bearing [J]. Journal of Zhejiang Sci-Tech University (Natural Sciences), 2014, 31(3): 221-227.
[7] MUSHI S E, LIN Zhongli, ALLAIRE P E. Design, construction, and modeling of a flexible rotor active magnetic bearing test rig [J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(6): 1170-1182.
[8] HUGHES T J R, COTTRELL J A, BAZILEVS Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39): 4135-4195.
[9] 尹硕辉, 余天堂, 刘鹏. 基于等几何有限元法的功能梯度板自由振动分析 [J]. 振动与冲击, 2013, 32(24): 180-186. YIN Shuohui, YU Tiantang, LIU Peng. Free vibration analysis of functionally graded plates using isogeometric finite element method [J]. Journal of Vibration and Shock, 2013, 32(24): 180-186.
[10]陈德祥, 徐自力, 刘石, 等. 求解Stokes方程的最小二乘等几何分析方法 [J]. 西安交通大学学报, 2013, 47(5): 51-55. CHEN Dexiang, XU Zili, LU Shi, et al. Least squares isogeometric analysis for Stokes equation [J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 51-55.
[11]陈德祥, 徐自力. 多重网格在黏性流动最小二乘等几何模拟中的应用 [J]. 西安交通大学学报, 2014, 48(11): 122-127. CHEN Dexiang, XU Zili. An application of multigrid in viscous flow simulations with least squares isogeometric method [J]. Journal of Xi’an Jiaotong University, 2014, 48(11): 122-127.
[12]COTTRELL J A, HUGHES T J R, BAZILEVS Y. Isogeometric analysis: toward integration of CAD and FEA [M]. Hoboken, NJ, USA: John Wiley & Sons, 2009: 164-165.
[13]BEIRAO V L, LOVADINA C, REALI A. Avoiding shear locking for the Timoshenko beam problem via isogeometric collocation methods [J]. Computer Methods in Applied Mechanics and Engineering, 2012, 241: 38-51.
[14]LEE S J, PARK K S. Vibrations of Timoshenko beams with isogeometric approach [J]. Applied Mathematical Modelling, 2013, 37(22): 9174-9190.
[15]刘伟. 结构振动超收敛等几何分析方法 [D]. 福建厦门: 厦门大学, 2014: 63-75.
[16]GENTA G. Dynamics of rotating systems [M]. Berlin, Germany: Springer Science & Business Media, 2007: 213-217.
[17]PIEGL L, TILLER W. The NURBS book [M]. Berlin, Germany: Springer-Verlag, 1997: 47-49.
[18]RAO S S. 机械振动 [M]. 4版. 李欣业, 张明录, 译. 北京: 清华大学出版社, 2009: 357-358.
(编辑 杜秀杰)
Isogeometric Timoshenko Beam Model and Numerical Verification for Active Vibration Control of Flexible Rotor
ZHANG Pengfei,WANG Zhiheng,XI Guang
(School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
A Timoshenko beam model with fewer degrees of freedom (DOFs) by isogeometric analysis method is proposed to be applied to active control of the flexible rotor and is numerically verified. This strategy solves the difficulties in the model from the standard FEM analysis, which cannot be directly employed for controller design due to the more DOFs. The isogeometric beam model with the semi-discrete form and the various boundaries are considered as the input signals in the active control for the rotor, then the singular value responses of the isogeometric beam models with more and fewer DOFs are compared, and the numerical solutions of isogeometric beam models with more and fewer DOFs and theoretic solutions both with simple supports are also compared. The rotor supported by the magnetic bearing and under the disturbances by the given distributing unbalance forces is simulated by the decentralized PD method. The results show that the singular responses of the model with fewer DOFs almost agree with those with more DOFs within the range of the sixth critical speed; the numerical solutions with more DOFs agree well the theoretic solutions within the first ten modal frequencies and the relative error of the first four modal frequencies from the model with fewer DOFs is less than 0.2%; the deviation of the steady displacement responses from the unbalance vibration between the isogeometric models with more and fewer DOFs is small and their steady response deviation can be regarded as the small disturbances with the same frequency at the working speed. The feasibility of applying directly for controller design is verified by the higher accuracy of the fewer DOFs isogeometric beam model within the low frequency range.
isogeometric method; flexible rotor model; Timoshenko beam; vibration control; magnetic bearing
2016-01-15。
张鹏飞(1989—),男,博士生;席光(通信作者),男,教授,博士生导师。
国家自然科学基金资助项目(51236006);中央高校基本科研业务费专项资金资助项目(XJJ2013002)。
时间:2016-07-14
http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1721.014.html
10.7652/xjtuxb201610021
O347.6; TH133.3
A
0253-987X(2016)10-0139-08
