基于光束平差法的宽基线双目三维重建

张家旺

（四川大学计算机学院，成都　610065）

基于光束平差法的宽基线双目三维重建

张家旺

（四川大学计算机学院，成都610065）

传统的基于图像矫正的双目三维重建方法对于图像的矫正结果有很强的依赖性，而宽基线的图像矫正很难获得理想的效果。针对该问题，提出一种无需矫正的基于光束平差法的宽基线双目三维重建方法。该方法利用双目视觉的几何约束恢复出相机姿态以及三维点云，然后利用光束平差法对相机姿态、相机内部参数以及三维点云进行优化，最终得到物体的三维模型。

立体视觉；光束平差；三维重建；宽基线

0　引言

三维重建是计算机视觉最主要的研究方向之一，在诸多领域，例如无人驾驶、机器人导航、文物数字化等，一直都是一个充满挑战的难题。三维重建主要通过对同一物体从不同视角拍摄二维图像以恢复出物体的三维模型。根据所依赖的不同视角的数量可将三维重建方法分为双目三维重建和多目三维重建（多视图三维重建）。本文仅讨论双目三维重建。

双目三维重建通过模拟人眼成像技术，利用摄像机从不同角度拍摄物体并恢复出物体的三维结构。双目三维重建方法主要分为两类：一类是基于图像矫正的双目重建；另一类是基于摄像机姿态估计的双目重建方法[1-2]。前者使用经过矫正的图像进行重建，能得到很好的效果。但对于宽基线的图像，往往得不到理想的矫正效果，从而无法对其进行三维重建。后者通过对图像进行摄像机姿态估计，对宽基线的情况具有良好的重建效果。

1　摄像机模型

摄像机的基本成像模型，通常称为基本针孔模型，由三维空间到平面的中心投影变换所给出[1]。摄像机模型抽象为数学模型可用投影矩阵P表示,投影矩阵分解为摄像机内参矩阵K，摄像机外参矩阵M,外参矩阵M可分解为旋转矩阵R和平移矩阵T，因此摄像机投影矩阵表示为：

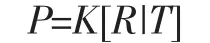
摄像机成像模型可表示为：

x=PX=K[R|T]X

2　摄像机姿态估计

两幅图像间的对级几何[3]约束，为摄像机的姿态估计提供了理论基础。对级几何是两幅图像间点、线关联的关系，这种关系可用基本矩阵[2，4]来进行代数描述。在计算机视觉中，基本矩阵F是一个3×3的矩阵，表达了立体像对的像点之间的对应关系。在对级几何中，对于立体像对中的一对像点，它们的其次化坐标分别表示为x与x'，Fx表示一条必定经过x'的直线（极线），这意味着立体像对的所有像点都满足：

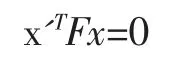
本质矩阵E也满足类似的关系，但本质矩阵并不蕴含摄像机内部参数，本质矩阵与基本矩阵之间的关系可由下式表达：

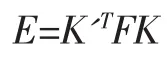
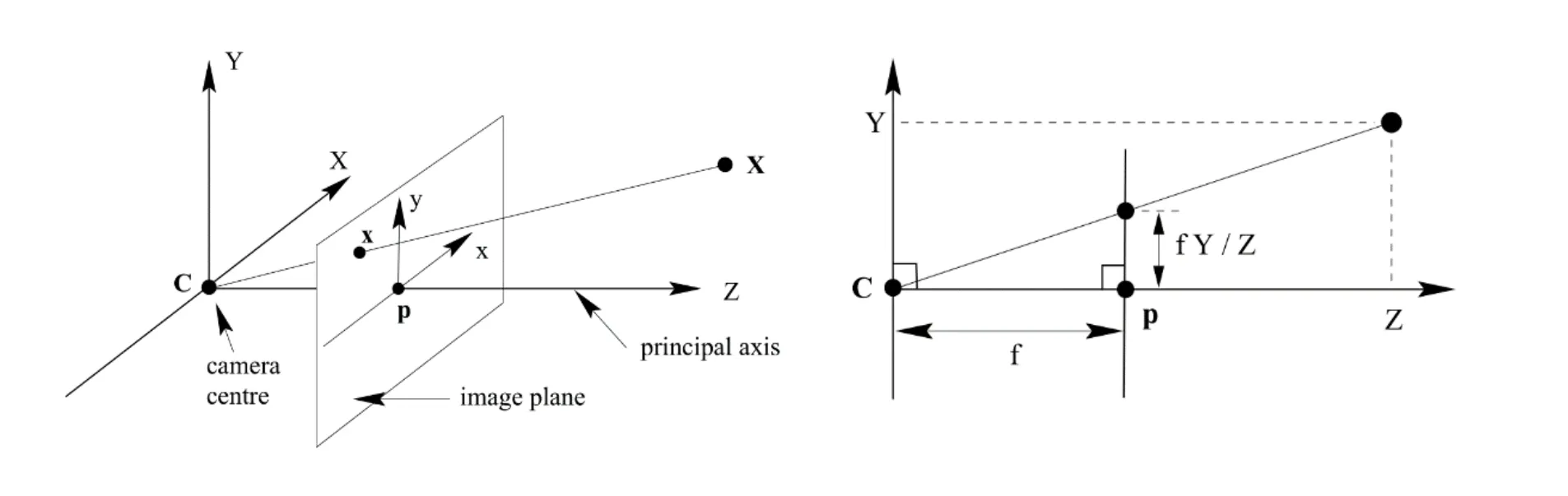
图1　摄像机模型

其中，K'和K分别为两个摄像机的内参矩阵。由一组对应像点，利用正则八点法可得到基本矩阵F，进而得到本质矩阵E[2]。本质矩阵可分解为两摄像机的相对旋转矩阵R和像对平移矩阵T。假设一摄像机为：

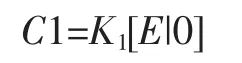
则另一摄像机可表示为：

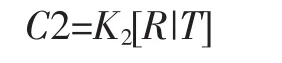
3　三角原理

在摄像机矩阵已知的情况下，三维重建的基本方法就是三角原理[2]。已知两摄像机矩阵分别为P与P'，x ↔x'为两幅图像的一组对应点。现在要恢复它们的三维空间点X，即满足：

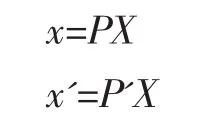
对于第一张图像有：

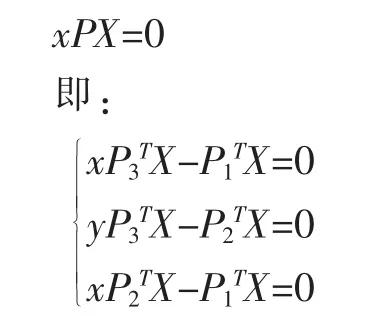
其中PiT为P的第i行，于是可得到形如AX=0的线性方程组：

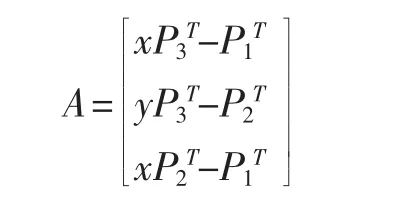
通过解AX=0，求得三维空间点坐标X。

4　光束平差法

光束平差法[2，5]是目前许多由运动到结构问题的标准算法，其最终目的归结为：减少观测像点与预测像点之间投影变换的误差。最小化误差算法采用最小二乘法，目前使用最为广泛的是Levenberg-Marquardt[6]，具有易于实现，收敛速度快的优点。

假设有n个三维空间点，m个摄像机，xij为第i个三维点在第j个摄像机像平面上的投影，光束平差法优化摄像机参数p和三维空间点坐标X，使得投影误差最小，即：

其中Q（Pj，Xi）表示三维空间点Xi投影到摄像机Pj的像平面的预测像点，d（x，y）表示像点x与y之间的欧氏距离。

摄像机矩阵P、P'以及通过三角原理获得的初始三维点X，通过光束平差法进行优化，最终得到相当精确的结果。

5　实验结果分析

实验环境为Ubuntu 15.10，Pentium Dual-Core CPU E6600@3.06GHz，4GB RAM。实验使用了2组公开数据集[6]，每组选取两个视角的图片，运用本文所提出的方法分别对其进行重建，最终效果如图2，实验运行时间见表1。

表1　运行时间

图2　（第一行为两组数据集原图，每组两张图片；第二行为两个数据集对应三维点云）

[1]吴福朝.计算机视觉中的数学方法[M].科学出版社,2008.

[2]Hartley R,Zisserman A.Multiple View Geometry in Computer Vision[M].Cambridge University Press,2003.

[3]Zhang Z,Deriche R,Faugeras O,et al.A Robust Technique for Matching Two Uncalibrated Images Through the Recovery of the Unknown Epipolar Geometry[J].Artificial intelligence,1995,78(1):87-119.

[4]Luong Q T,Faugeras O D.The Fundamental Matrix:Theory,Algorithms,and Stability Analysis[J].International Journal of Computer Vision,1996,17(1):43-75.

[5]Triggs B,McLauchlan P F,Hartley R I,et al.Bundle Adjustment-a Modern Synthesis[M].Vision Algorithms:Theory and Practice. Springer Berlin Heidelberg,2000:298-372.

[6]Moré J J.The Levenberg-Marquardt Algorithm:Implementation and Theory[M].Numerical Analysis.Springer Berlin Heidelberg,1978: 105-116.

[7]Furukawa Y,Ponce J.Accurate,Dense,and Robust Multiview Stereopsis[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2010,32(8):1362-1376.

Stereo Vision;Bundle Adjustment;3D Reconstruction;Wide-Baseline

Wide-Baseline Stereo Reconstruction Based on Bundle Adjustment

ZHANG Jia-wang

（College of Computer Science，Sichuan University，Chengdu 610065）

The traditional method of stereo reconstruction based on rectified image has a strong dependence on the result of the image rectification, while wide-baseline always resulting in a bad rectification result.To solve this problem,proposes a wide-baseline stereo reconstruction method based on bundle adjustment.An initial point cloud,which can be get from the epipolar geometry constrains of the images,camera pose and internal parameters are optimized with bundle adjustment.

1007-1423（2016）32-0071-03

10.3969/j.issn.1007-1423.2016.32.016

张家旺（1990-），男，河北保定人，硕士，研究方向为计算机视觉、三维重建

2016-10-13

2016-11-05