平面上任意凸多边形面积的计算
2016-12-21廖祥超郭民之
廖祥超+郭民之

摘要:以平面上任意有限个点为顶点的凸多边形面积的计算是一个很有实用价值的问题,该文结合平面解析几何相关知识,用数学归纳法先推导出平面上凸n边形面积的一般计算公式,然后利用Excel中多个函数和排序技巧实现了面积的程序化计算,并用实例演示说明。最后讨论了如何用这种方法去计算平面上任意凸多边形的面积。
关键词:平面凸多边形;顶点逆时针排序;面积公式;Excel程序化计算
中图分类号:TP37 文献标识码:A 文章编号:1009-3044(2016)28-0245-02
Abstract: It is a quite practical and valuable problem about the calculation of the area of convex polygon which is formed by arbitrary point on the plane. Based on the relative knowledge of Analytic Geometry, the formula for the calculation of the area of convex polygon was deduced and proved by Mathematical Induction in this paper; then many functions and skills of sorting were used in Excel, which helps it realize the goal of programming calculation of the area of convex polygon in the example. Finally, they discussed this method about the calculation of the area of arbitrary convex polygon on the plane.
Key words: convex polygon on the plane; vertex with anticlockwise sort; formula of area; programming calculation in excel
1 引言
平面解析几何是数形结合的典范,它通过建立平面直角坐标系把点与有序数对联系起来,把图形和方程对应起来,用代数方法来研究几何问题,以几何直观来解释代数结论。
计算凸多边形面积传统的方法是把凸n边形分割成n-2个三角形,然后累加各三角形的面积得到其面积。近年来,国内有许多学者借助Excel研究凸多边形面积计算的问题,文献[1][2][3][4]中均用梯形法给出凸多边形的面积计算公式,但是或多或少存在一些不足,有的文献证明不够严谨;虽然强调图形的闭合性,但是在面积计算公式中的表述不够严格;还有顶点按逆时针或顺时针方向排序时,面积的正负号的区分没有交代清楚。基于以上事实,本文提出了一个凸n边形顶点按逆时针方向排序的方法,给出并证明了凸n边形面积的计算公式。在示例中,本文先运用Excel自带的相关函数对这n个顶点按逆时针方向排序,再画出凸多边形的图形,最后求出其面积。
为了将凸多边形的n个顶点按逆时针方向排序,我们先找出n个顶点中最靠左和最靠右的两个顶点(假设这种点是唯一的,若不唯一,我们可通过简单的旋转变换,使其在新坐标系中唯一),分别设它们为和,即,分别是横坐标最小和最大的顶点。那么过和的直线l就可以将所有的顶点分为上下两组。然后将下面一组顶点按横坐标从小到大排序,而上面一组顶点按横坐标由大到小排序,最后将排序后的两组顶点合并在一起就可以得整个凸多边形n个顶点按逆时针方向的一个排序,对排序后的凸n边形,下面的定理给出了其面积的计算公式。
2.2 凸n边形面积公式
定理1 设是任意凸多边形的按逆时针方向排序后的n个顶点,则该多边形的面积为
证 运用数学归纳法证明。当凸多边形边数n=3时,如图1:
这里只对图1左图情形给出证明,右图情形证明方法类似。
假设当n=k时,(2)式成立,那么当n=k+1时,如图2:
即n=k+1时(2)式成立。
3 实例分析
下面我们以凸九边形为例,来演示说明在Excel 2010中如何求出对应的凸九边形的面积。设为凸九边形的9个顶点,具体的坐标值(注:可随意给出,只要它们可围成一个凸九边形即可)见图3中单元格区域B2:C10。
步骤①:找出和,然后确定直线.
为了找到横坐标最小的顶点和最大的顶点,可使用查找函数“VLOOKUP”:在H3输入“=VLOOKUP(MIN(B2:B10),IF({1,0},B2:B10,A2:A10),2,0)”,得到的是P1;在H4输入“=VLOOKUP(MAX(B2:B10),IF({1,0},B2:B10,A2:A10),2,0)”,得到是P7。与顶点对应的坐标的值可在单元格I3和J3输入图3中批注的命令获得,选中单元格I3:J3向下填充即可得到的坐标。根据(1)式,在H7、H8、H9中分别键入公式“=J4-J3”、“=I3-I4”、“=I4*J3-I3*J4”,就可以得到A、B、C的值,于是直线l的方程为:
步骤②:排序
在D2中键入“=$H$7*B2+$H$8*C2+$H$9”,往下填充至D10就可求得各点对应的的值;为了方便分组和排序,我们令
在E2中键入“=IF(D2>=0,1, -1)”,再向下填充至E10,结果如图3所示。由B= -15.2<0,据表1易知的点Pi是在直线l的下方,而的点Pi则是在直线l的上方。利用INDEX函数查找相同内容,返回对应值的名称这一功能,我们可在G13中输入“=INDEX(A:A,SMALL(IF(E$2:E$10=1,ROW($2:$10)),ROW(E1)))”,然后再同时按下Ctrl+Shift+Enter,就可以找到满足的第一个点P1,匹配顶点P1的横纵坐标可用图4批注中的命令确定;选中单元格G13:I13,向下填充至G16:I16即可得到满足的其余三个点P4、P5、P6;在J13中输入“=INDEX(G$13:G$16,MATCH(SMALL(H$13:H$16,ROW(J1)),H$13:H$16,0))”,按下Enter键,公式将返回最小的点的名称P1,再向下填充至J16,即可得到在直线l下方且按逆时针方向排序后的顶点P1、P6、P4、P5.
同理我们可以找到满足这组点。这时按降序排序,我们得到位于直线l上方且按逆时针方向排序的顶点P7、P9、P3、P2、P8,相关命令如图5批注所示:
步骤③:画出凸九边形并求其面积
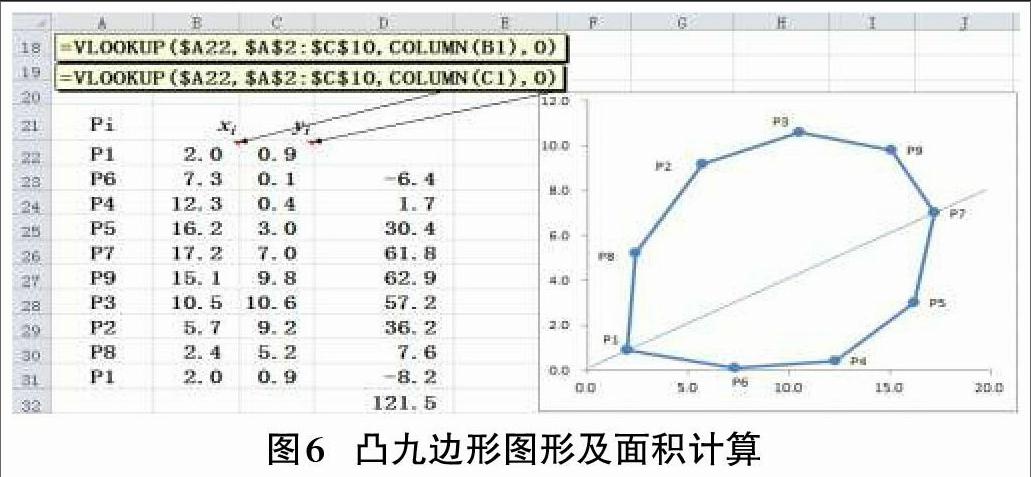
复制J13:J16,O13:O17的内容,分别粘贴(注意粘贴选项为值)到A22、A26中即可得到凸九边形9个顶点逆时针方向的一个完整排序P1,P6,P4,P5,P7,P9,P3,P2,P8;然后在A31再输入P1,匹配顶点坐标方法类似前面,命令见图6批注。选取数据区域B22:C31,然后单击【插入】/【散点图】/【直线和带数据标记的散点图】,即可画出凸九边形。在D23中输入“=B22*C23-B23*C22”,按下Enter键再向下填充至D31,然后在D32中键入“=1/2*SUM(D23:D31)”,即可算出凸九边形的面积为121.5(参见定理1公式(2))。以上操作结果如图6所示。
4 讨论
上述计算凸九边形的方法和步骤具有一般性,对任意凸n边形面积的计算只需调整一下n个坐标点所在的单元格区域即可,操作起来是比较方便的。不管n的大小,只要保证凸多边形的顶点按逆时针方向排序即可,即先找出横坐标最小和最大的两点来确定直线l,然后分别查找在直线l下方和上方的点,分别按逆时针方向排序后再合并为一组,得到凸n边形顶点的一个完整的逆时针排序。最后根据定理1仿照图6的操作求出凸多边形面积。注意步骤①②只需修改函数的使用范围,步骤③还需调整放置区域。
参考文献:
[1] 陆春雨.巧用Excel计算多边形面积[J].河南水利,2001(2).
[2] 吕红虎.用Excel计算面积[J].城市勘探,2000(1).
[3] 黄美添.用Excel工作表编制面积计算程序[J].西部探矿工程,2007(8).
[4] 毛爱国.用Excel法计算多边形面积[J].农业科技情报,2014(3).
[5] 王巧伶.Excel2010函数应用速查手册[M].北京:机械工业出版社,2012.
[6] 韩小良.Excel2003/2007公式与函数的使用艺术[M].北京:中国铁道出版社,2008.
