基于模糊物元的云南省工程型缺水程度分析

2016-12-21谭平，梁媛

水电站设计 2016年4期

关键词：欧氏物元缺水

谭平，梁媛

(中国电建集团成都勘测设计研究院有限公司，四川成都 610072)

基于模糊物元的云南省工程型缺水程度分析

谭平，梁媛

(中国电建集团成都勘测设计研究院有限公司，四川成都 610072)

工程型缺水是西南地区的主要缺水形式。目前国内对于工程型缺水程度的界定尚未有统一的标准，分析尚无明确方法。本文尝试将模糊物元模型和欧氏贴近度引入到工程型缺水程度分析中，以云南省各州市和工程型缺水各阶段作为物元事物，建立评价指标体系；并在基于层次分析法的基础上应用熵权法确定权重，通过计算与标准模糊物元之间的欧氏贴近度，确定工程型缺水程度。本文提出了一种基于熵权的模糊物元工程型缺水分析方法，并将该方法应用于云南省所有16个市、州的工程型缺水程度分析，并提出了相应的对策措施，为工程型缺水分析提供一种新思路。

工程型缺水；模糊物元；熵值法；欧氏贴近度；云南省

0 前言

工程型紧缺是指由于水工程开发建设滞后，水资源时空调配失衡，造成供水量不足而引起的水资源紧缺[1]。一些处于水资源丰富地区的城市和地区由于供水工程建设不足，也会出现工程型缺水。如2010年西南地区大旱，云南省等水资源较丰富的地区也出现了缺水现象情况，大部分地区干旱等级升至百年一遇以上，暴露出云南水利基础设施仍然薄弱的局面。虽然经过多年努力，云南水资源供水状况有了很大改善，但工程型缺水仍是云南主要的缺水形式[2]。

目前国内关于工程型缺水程度的研究较少，对其程度还没有统一的界定标准。在四川省缺水城市缺水报告分析[3]中提出城市工程型缺水的评价标准为：缺水率大于20%，则认为该城市为严重缺水城市，并通过建立指标体系，计算需水量和工程可供水量，得出缺水率，最终确定出四川省各城市的工程型缺水程度。

模糊物元法在水资源分析中应用较广，袁华等[4]采用模糊物元分析方法，结合欧氏贴近度的概念，按照社会-经济-生态环境-资源-效率合理性指标建立水资源调配评判指标。对黑河流域5种可能的水资源配置方案进行分析，选出最佳配置方案。马明卫等[5]采用基于信息熵理论的模糊物元分析法对榆林市水资源可持续利用进行评价，并在此基础上进行合理的改进和运用，结合欧氏贴近度实现不同评价分区的量化比较，得到各分区水资源可持续利用水平及其优劣次序。本文在物元分析的基础上，结合欧氏贴近度，并在基于层次分析法的基础上应用熵权法确定权重，避免AHP法确定权重的主观性。构建基于熵权的模糊物元模型，并对云南省城市工程型缺水程度进行比较分析。

1 模糊物元模型原理

1.1 模糊物元和复合模糊物元

给定事物的名称N, 它关于特征c有量值为v,以有序三元R=(N,c,v)组作为描述事物的基本元, 简称物元。其中, 量值v具有模糊性, 便称为模糊物元。如果事物N有n个特征c1,c2, …,cn和相应的模糊量值v1,v2, ...,vn, 称R为n维模糊物元,简记为R=(N,c,v)。如果m个事物的n维物元组合在一起, 使构成m个事物n维复合物元Rmn。若将Rmn的量值改写为模糊物元量值, 称为m个事物n维复合模糊物元[6,7], 记作

(1)

式中Rmn为m个事物n维复合模糊物元；Mi为第i个事物,i=1,2,…,m;ck为第k项特征，k=1,2,…,n;uik为第i个事物第k项特征对应的模糊量值。

1.2 从优隶属度的确定

模糊量值u(x)表示与事物特征C相应量值x的隶属度。

越大越优。其变换公式为：

(2)

越小越优。其变换公式为：

(3)

越接近某个常数越优。其变换公式为：

(4)

上面三个公式中uij是j个事物第i项指标(特征)的从优隶属度；maxxij是各评价事物中每一项指标所有的xij量值中的最大值；minxij是各评价事物中每一项指标所有的xij的最小值，u0为该项指标的标准值。

1.3 标准模糊物元与差平方复合模糊物元

由式(1)可以构成标准方案的n维模糊物元R0n,其中各项由Rmn中各方案从优隶属度中的最大值或最小值确定,则得到

(5)

若以Δij(j=1,2,∧,m;i=1,2,∧,n)表示标准模糊物元R0n与复合模糊物元Rmn中各项差的平方，则组成差平方复合模糊物元RΔ , 即

(6)

其中Δji=(u0i-uji)2,(j=1,2,∧,m;i=1,2,∧,n)

1.4 基于熵值的权重确定

熵是系统无序程度的度量，可以用于度量已知数据所包含的有效信息量和确定权重。当评价对象指标值相差较大时，熵值较小，说明该指标提供的有效信息量较大，其权重也应较大；反之，若某项该指标值相差较小，熵值较大，说明该指标的信息量较小，其权重也应较小[8-9]。可以消除AHP等方法确定权重的主观因素，其计算步骤如下：

(1)构建m个事物n个评价指标的判断矩阵R

R=(rij)m×n(i=1,2…,n;j=1,2,…,m)

(7)

(2)将判断矩阵R进行归一化处理，得到归一化矩阵B，B的元素为

(8)

式中 rmax、rmin分别为同一评价指标下不同对象中最满意者或最不满意者。

根据熵的定义，m个评价对象n个评价指标，确定评价指标的熵值

(9)

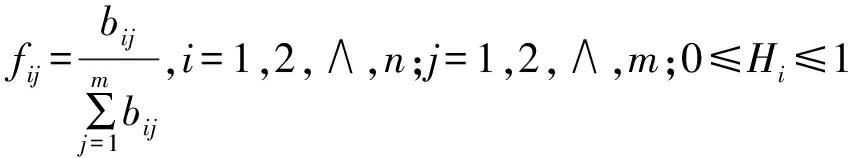
(10)

(3)利用熵值计算评价指标的熵权

(11)

(12)

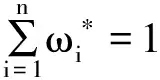
(4)计算评价指标的综合权重[10]

W=(ωi)1×n

(13)

(14)

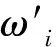
1.5 欧氏贴近度

贴近度是指被评价样本与标准样本两者相互接近的程度，其值越大表示两者越接近，反之则相离较远[11]。可用于两物元贴近度计算的公式有多种，考虑到本文具有综合评价的意义，采用欧氏贴近度进行计算[12]。

(15)

式中ρHj为第j个评价样本与标准样本的贴近度,由此来构造欧氏贴近度复合模糊物元RρH，即：

(16)

根据计算出的贴近度即可实现对各评价样本的优劣排序和类别划分。

2 云南省工程型缺水程度综合评价分析

本文选取2010年为现状水平年，收集云南省全部16个地市州(昆明市、曲靖市、玉溪市、保山市、昭通市、丽江市、普洱市、临沧市、楚雄彝族自治州、红河哈尼族彝族自治州、文山壮族苗族自治州、西双版纳傣族自治州、大理白族自治州、德宏傣族景颇族自治州、怒江傈僳族自治州、迪庆藏族自治州)的水资源、水利工程数据，对16个地市州的工程型缺水程度进行比较分析。所选数据全部来自于云南省统计年鉴、云南省水资源公报和云南省水利统计年鉴。

2.1 指标体系建立

评价指标确定的原则：一是要能够显著的表征区域工程型水资源短缺的程度;二是能够区分各地区缺水的类别;三是指标代表性好，具有很好的可操作性和实用性。

同时云南省水资源具有以下特点：地处我国西南边陲，由于横断山脉深度切割，高差悬殊，地形地貌复杂，水资源总量丰沛但开发利用的难度大、成本高、边际效益低。水生态环境脆弱，水环境承载能力低，防污治污任务重。水土流失面积超过国土面积的1/3。水利基础薄弱、防洪标准偏低，特别是农村水利工程普遍老化失修、带病运行，险工险段隐患多。根据云南省水资源特点，设置以下指标：

(1)水土流失面积比x1：水土流失面积与土地面积之比，%;

(2)农村饮水安全人口比x2：农村饮水安全人口与农村人口之比，%;

(3)人均供水量x3：水利工程总供水量与总人口之比，m3/人;

(4)有效灌溉面积比x4：有效灌溉面积与耕地面积之比，%;

(5)总库容系数x5：水利工程总库容/多年平均年径流量，%;

(6)达标堤防长度比x6：达标堤防长度与总堤防长度之比，%;

(7)水资源开发利用率x7：河道外供水量与多年平均水资源量之比，%;

(8)水利工程投资比x8：水利工程投资与总投资之比，%。

将工程型缺水程度分为5个等级，收集2000年～2010年共11年云南省各地市州的上述指标数据，进行聚类分析，将工程型缺水程度分为5个等级，得到5个分级标准的各自评价指标值，各评价指标分级标准如表1所示。

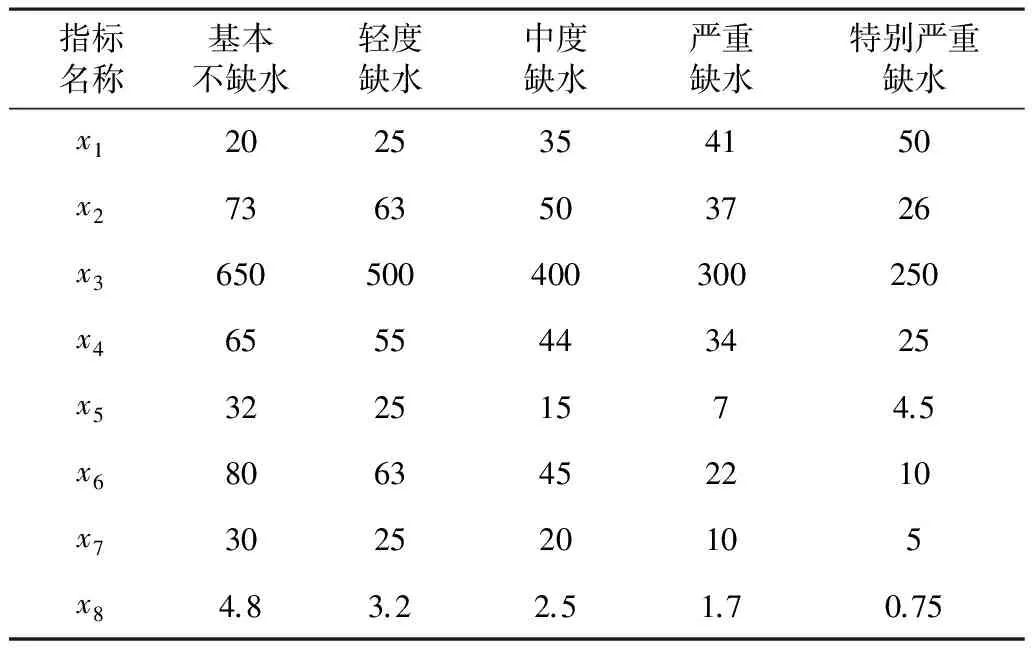
表1 各工程型缺水程度评价指标分级标准值

2.2 模型建立

(1)构建复合模糊物元。根据所收集的数据，对云南省16个地市州各评价指标值及5个分级标准方案，建立21个方案8个指标的复合模糊物元。

(2)根据式(2)～(4)计算从优隶属度。水土流失面积比按越小越优型计算，农村饮水安全人口比、有效灌溉面积比、达标堤防长度比等6个指标按越大越优型计算，水资源开发利用率按照常数型指标计算，取国际普遍采用的30%的水资源合理开发利用程度[13]为u0，即u0=30。

(3)根据式(5)和(6)构建得到差的平方复合模糊物元RΔ(下式用其转置矩阵表示)。

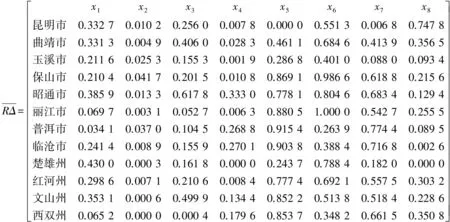
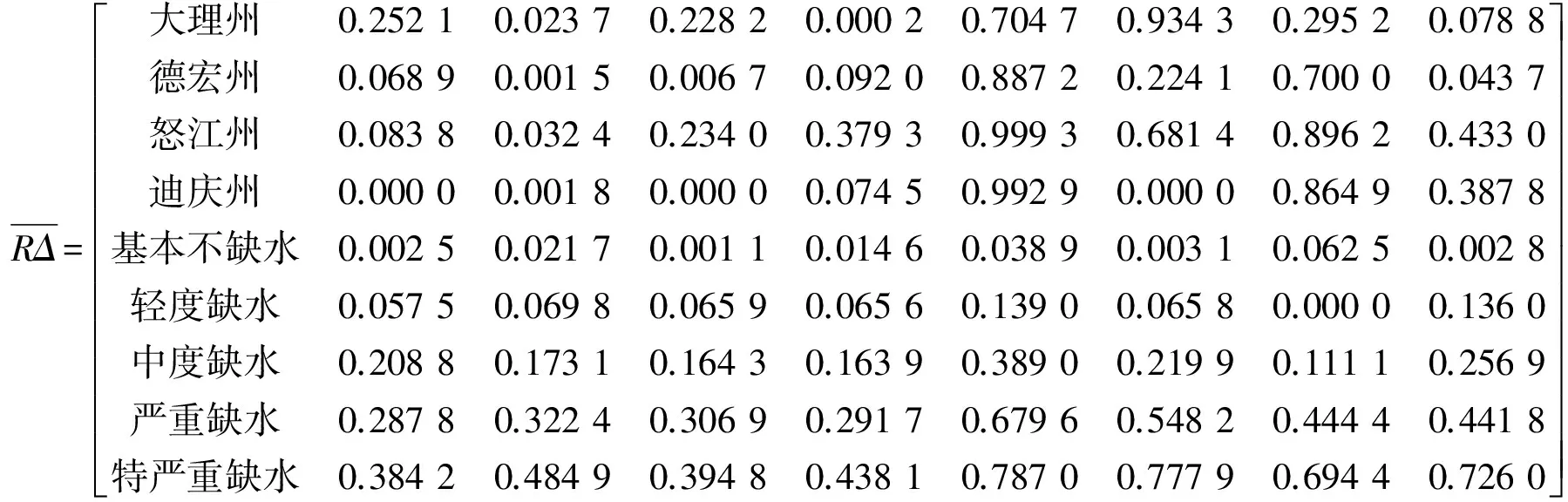
(4)采用熵值法确定指标的权重。首先根据各方案实测值构造判断矩阵，用层次分析法[14]求得主观权重集：

W*=(0.019 7,0.034 1,0.230 7,0.049,

0.157 5,0.071 8,0.330 7,0.106 5)

进行一致性检验，CR=0.035,满足一致性。

根据式(9)～(14)计算出各评价指标的权重

W′=(0.133 9,0.154 2,0.127 2,0.147 8,

0.125 0,0.106 7,0.115 6,0.089 6)

由式(15)计算得出各评价指标的综合权重：

W=(0.022 1,0.044 0,0.245 4,0.060 6,

0.164 6,0.064 1,0.319 6,0.079 8)

(5)欧氏贴近度的计算。根据求出的平方复合模糊物元和各指标权系数，由式(7)计算得到各方案的欧氏贴近度:

ρHj=(0.785 3,0.590 4,0.817 8,0.500 2,0.401 3,

0.582 2,0.533 5,0.536 8,0.775 9,0.541 7,0.494 1,

0.585 4,0.660 9,0.603 6,0.387 3,0.524 6,

0.991 0,0.928 7,0.803 4,0.562 2,0.387 6)

2.3 结果分析

根据欧氏贴近度的大小排序，云南省工程型缺水程度依次是玉溪市<昆明市<楚雄彝族自治州<大理白族自治州<德宏傣族景颇族自治州<曲靖市<西双版纳傣族自治州<丽江市<红河哈尼族彝族

自治州<临沧市<普洱市<迪庆藏族自治州<保山市<文山壮族苗族自治州<昭通市<怒江傈僳族自治州。由此可以得出结论：云南省的所有地市州存在不同程度的工程型缺水，云南省各地级市工程型缺水情况分布如图1和表2所示。

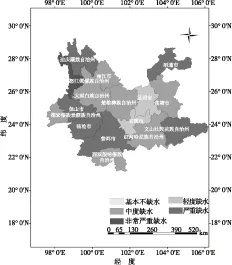
图1 云南省工程型缺水程度

表2 云南省各市、州欧氏贴近度计算结果

由图1和表1可以看出：云南的所有地市州存在不同程度的工程型缺水，其中根据图1，由于城市经济社会发展快，集中度高，库容系数大，水资源开发利用率高，昆明市和玉溪市工程型缺水程度较轻，为轻度工程型缺水城市。而云南省其余地区由于地形地貌复杂，水资源开发利用难度大，水资源开发利用率均很低，均存在较为严重的工程型缺水现象。其中，怒江州为特别严重工程型缺水城市，工程型缺水最为严重。怒江州地处云南滇西横断山脉纵谷地带，整个地势由巍峨高耸的山脉与深邃湍急的江河构成，有切割很深的怒江、澜沧江、独龙江三大峡谷的山区，水资源开发难度极大，水资源开发率很低。结果表明，基于熵权的模糊物元法的分析结果真实可信，可以合理评估研究区工程型缺水程度，为区域水资源开发提供决策依据。

2.4 对策措施

结合工程型缺水计算结果、资料收集分析及现场调查情况，制定了以下的对策措施。

怒江州和文山州特别要解决好“望天田”的灌溉问题，在地理地形条件不能兴建水库、堰陂的地方也要采取打机井、挖水窖等办法蓄水灌溉；在电力发达，电能富余而又水资源紧缺的地方因地制宜兴建一批抽水泵站和蓄水池，利用峰谷电源提水增蓄储备水资源，彻底消灭灌溉“盲”区。加大园田化建设力度，平整土地，对灌排渠系截弯取直、加固防渗，改善输水条件，提高水的利用率。

改革传统灌溉模式，推广滴灌、喷灌、雾灌等节水灌溉技术。我国农业灌溉一直采用传统的流灌、漫灌、浸灌、沟灌等方法，有水自然流，无水向天求。目前各用水农户普遍存在浪费水现象，用水效益不高。我国的用水总量和美国相当，但GDP仅为美国的1/8。农民仍然习惯于大水漫灌，全国农业灌溉水的利用系数平均约为0.43，而先进国家为0.7甚至0.8。我国作物水分生产率平均为0.8kg/m3粮食，只相当于发达国家的40%。不少学者研究指出我国农业用水的节水潜力十分巨大。迪庆州、西双版纳州和楚雄州如果全面采用喷灌、滴灌、雾灌、微灌、渗灌等节水技术，水资源紧缺情况将得到很大缓解。所以，各级政府要采取切实有效措施，宣传群众，动员群众，支持和激励群众建设节水灌溉网络，推广节水灌溉技术，开展节水灌溉。

临沧市和德宏州应对现有水利工程更新改造和清淤扩容，挖潜增蓄。增加工程蓄水和解决农村灌排“跑、漏、冒”的问题，从根本上改变“上游水下河，下游干死禾”的现象。这项工作大有潜力可挖，粗略估算如全部蓄水工程清淤到位，工程蓄水将有望增加30%～40%。

怒江州和迪庆州应加大水土流失的治理力度，多种树木、草皮，增加植被，含养水份，减少水份蒸发。

云南省以种植耗水量大的水稻为主，以2005年为例，亩均耗水量450m3，有些地方高达600m3/亩以上，加上工程型缺水，供需矛盾更加突出。怒江州和迪庆州可因地制宜调整种植结构，逐步减少水稻种植面积，引种一些低耗水的高原农旱作物，扩种一些耐旱的经济作物，做到种植结构调整不影响农业和农民的增产增收。

3 结论

基于熵权的模糊物元法通过直接选取与工程型缺水有关的指标，采用熵法求得权重，避免了AHP法的主观性，通过计算欧氏贴近度评估工程型缺水程度，并提出了相应的对策措施。该模型在云南省的应用结果表明，方法的分析结果真实可信，与事实较为吻合，较以往的方法相比针对性更强，更具备推广价值。在以后的研究工作中，可以将该方法应用在同样工程型缺水问题较为严重的川、渝、黔、桂等地区进行分析，为解决我国西南地区工程型缺水问题提供参考。该方法为城市工程型缺水程度分析提供了一种新的思路，为解决工程型缺水问题提供决策依据。

[1] 许新宜,王韶伟,庞博，等. 水资源紧缺类型及其对策分析研究[J]. 北京师范大学学报(自然科学版), 2009,45(2):86-90.

[2] 王建春,高嵩,顾世祥,杨树德. 云南省水危机及对策措施研究[J]. 中国农村水利水电,2010(12):52-56.

[3] 四川省城市缺水分析报告[R].四川省水利厅,2011.

[4] 袁华,牛少凤,袁伟，等. 黑河流域水资源调配评价的模糊物元分析法[J]. 中国农村水利水电,2007(12):22-25.

[5] 马明卫,张鑫,蔡焕杰，等. 基于熵的模糊物元水资源可持续利用评价[J]. 人民长江,2009,40(7):7-10.

[6] 蔡文. 物元模型及其应用[M].北京:科学技术文献出版社,1994.

[7] 张斌,雍歧东,肖芳淳.模糊物元分析[M].北京:石油工业出版社,1997:1-50.

[8] 邱菀华.管理决策与应用熵学[M].北京:机械工业出版社,2001.

[9] 闫文周,顾连胜.熵权决策法在工程评价中的应用[J].西安建筑科技大学学报,2004,36(1):98-100.

[10] 阮本清,韩宇平,王浩，等.水资源短缺的模糊综合评价[J]. 水利学报,2005,36(8):906-912.

[11] 肖芳淳. 模糊物元贴近度聚类分析的研究[J]. 新疆石油地质,1999,19(4):281-283.

[12] 潘峰,梁川,王志良，等.模糊物元模型在区域水资源可持续利用综合评价中的应用[J]. 水科学进展,2003,14(3):271-275.