混凝土坝表面的干缩应力

吴 一 匡

(浙江水利水电学院， 浙江 杭州 310018)



混凝土坝表面的干缩应力

吴 一 匡

(浙江水利水电学院， 浙江 杭州 310018)

库水位下降，混凝土坝等大体积混凝土内的水分，要从混凝土表面扩散到空气，从而使混凝土干缩出现表面裂缝。本文求解半无限混凝土体的湿度扩散微分方程，用Laplace变换法算出干缩弹性应力，并以实例验算。

湿度扩散微分方程;干缩深度；0应力深度；平衡湿度。

1 湿度扩散微分方程

混凝土内水分扩散规律与温度传导规律相似，但是水扩散速度比温度传导速度要慢得多，因此大体积混凝土内水分的变化主要局限在表层，内部变化不大。y座标0点在半无限混凝土表面，y轴指向混凝土深处，t是时间，k是混凝土内水分扩散系数,例如k=0.000 005 m2/h，比导温系数小1 000倍，β是混凝土表面水分交换系数,例如β=0.000 2 m/h，空气边层厚度δ=0.000 005/0.000 2=0.025 m,U是混凝土湿度kg/kg，即每kg混凝土中所含水分重量kg，混凝土初始湿度U0均匀分布,Uβ是混凝土平衡湿度,即长时间最终达到的湿度, 其值取决于空气相对湿度及混凝土本身特性，当空气湿度降低20%～30%时,U0-Uβ=1%, 湿度扩散微分方程与热传导微分方程类似，定解问题是:

(1)

U(y,0)=U0=U(∞,t)

(2)

(3)

(4)

方程(1)在条件(2)下变换为

边界(3)变换后解岀c再代入上式得

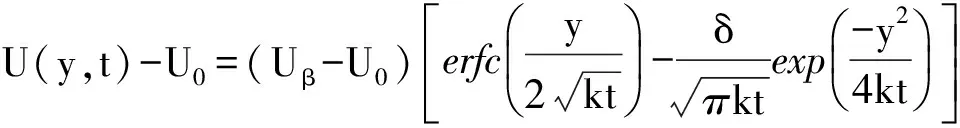
(5)

erf(x)=x/2+0.3436sin[π(1-x/2)]-

0.027sin[π(2-x)],(x<2);

erf(x)=1,(x>2)

(6)

例题1 大体积混凝土，水分扩散系数k=0.000 005 m2/ h，表面水分交换系数β=0.000 2 m/h，空气边层厚度δ=0.000 005/0.000 2=0.025 m，计算相对湿度:

把(6)代入上式，算出相对湿度，见表1。

从表中可以看出，相对湿度变化缓慢，且局限在表层。

2 干缩应力

从表1中查岀干缩深度y米，例如t=8 760 h、

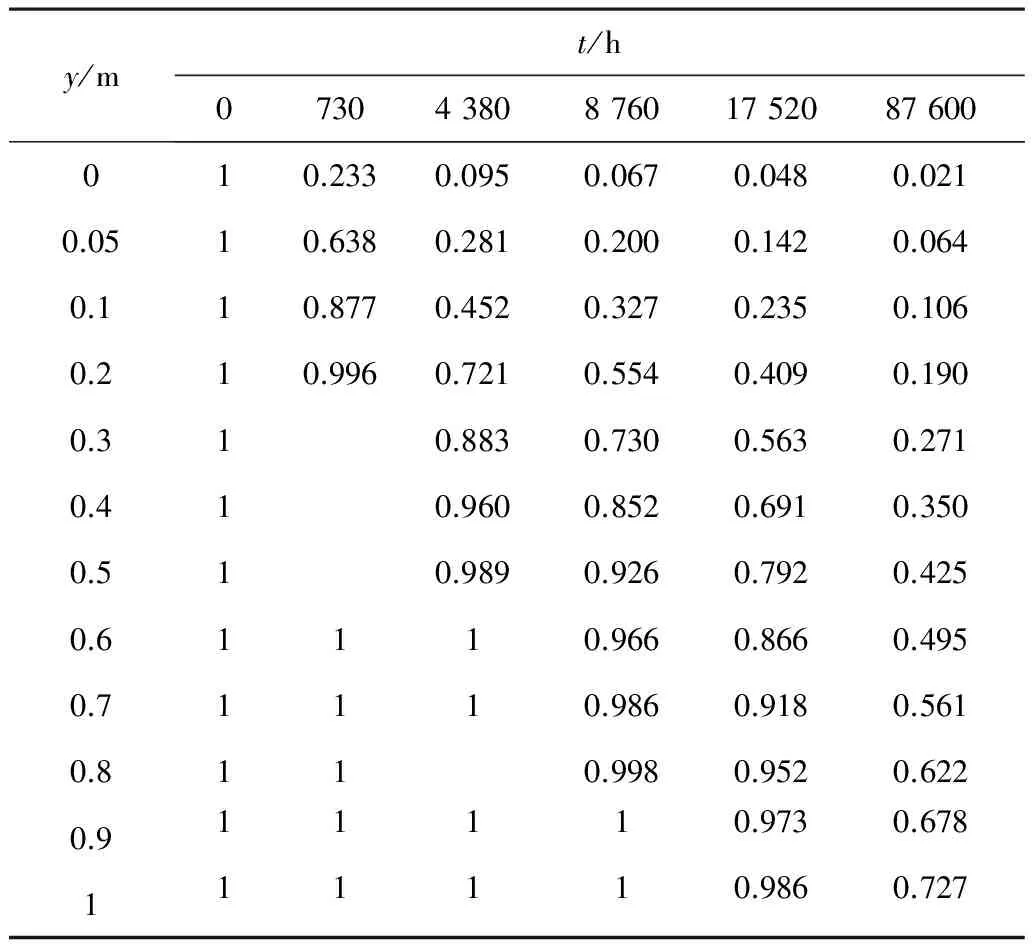
表1 相对湿度[U(y,t)-Uβ]/[U0-Uβ]计算

干缩深度y=0.8 m，再用一条抛物线计算平均相对湿度:

从S.Timoshenko《弹性理论》，干缩应力为：

(7)

式中，混凝土弹性模量E=24 000 MPa，收缩系数α=0.005 0, 泊松比v=1/6, 湿度U0-Uβ= 0.01。

例题2 题目同例题1，试计算t=8 760 h的干缩应力:

表2 t=8 760 h的干缩应力

从表2可以看出，坝面σ= 0 MPa，应力深度y=0.313 m。

[1] 朱伯芳.大体积混凝土温度应力与温度控制[M].电力出版社,1999.

[2] 刘伟才，蔡现阳.大花水水电站大坝裂缝处理工艺与质量控制[J].水电站设计,2010.

[3] 吴一匡.混凝土面板堆石坝的干缩应力[J].土石坝技术,2012.

2014-09-15

吴一匡(1933-)，男，浙江杭州人，副教授，从事温度场及定向爆破研究工作。

TV641.43

B

1003-9805(2016)04-0043-02