共同因子冲击下的股票市场与经济增长的互动关系研究——基于中国与OECD国家股市与经济数据的分析
2016-12-21崔华泰
崔华泰
(中国人民大学 经济学院,北京 )
经济研究
共同因子冲击下的股票市场与经济增长的互动关系研究
——基于中国与OECD国家股市与经济数据的分析
崔华泰
(中国人民大学 经济学院,北京 )
在中国经济社会面临深刻转型的背景下,资本市场的作用尤为凸显,资本市场的改革、创新和发展对中国经济复苏、结构调整和增长方式的转变具有重大意义。在此基于1992—2012年OCED国家与中国的面板数据,对股票市场与经济增长的关系进行了实证研究。在研究中,为了控制技术革新、经济周期等共同冲击的潜在影响,对Holly、Pesaran提出的CCEP的实证方法加以改进,发现股市发展程度、股市换手率、股市规模程度、政府对经济的干预度、经济集聚度均对实际人均收入所代表的经济增长起到不同方向、不同程度的影响。同时,发现共同因子较好地刻画了技术冲击、经济周期因素等共同冲击对各个国家经济增长的影响,并从因子载荷系数的估计中发现,经济体的经济规模越大,对于共同冲击的反应越强烈。
股票市场;经济增长;共同因子;CCEP模型
早在1891年,就有学者在资本市场对经济增长的影响领域进行研究,学术界大量涌现这方面的研究始于上个世纪的八十年代。内生金融理论的诞生为股市发展与经济增长之间的理论联系注入了新的活力,学者们开始在不同的领域和视角(资本形成效率、风险分散、信息传递)对股票市场和经济之间进行深入系统的研究,希望找到两者之间的奥秘。
Beck和Levine(2001)对40个国家1976-1998年的数据进行平均面板数据回归,在控制了个体自回归和潜在内生性后,得出股票市场的流动性对经济增长有积极影响的结论。Arestis、Demetriades和Luintel(2001)对1973-1998年间的美股交易率和换手率与经济增长的数据进行了实证分析,测算出这两者对GDP有正向作用。Chang(2011)发现在股票市场刚起步的国家,股市与经济增长有明显的正相关关系,但在股市已发展成熟的国家,这种关系却不太明显。Christopoulos和Tsionas(2014)运用面板数据分析了10个发展中国家1970-2010年的数据发现,投资支出、通货膨胀、金融发展与经济增长之间存在一个显著的协整矩阵向量,并且股市发展与经济增长之间存在因果关系。Apergis和Filippidis(2007)对Beck和Levine(2014)研究中的不足进行了修正,考虑到了不同国家的样本异质性问题,根据发展水平将65个国家分为15个OECD国家和50个欠发达国家两个部分,对这两个部份分别进行实证分析,结果均验证股票市场发展对经济增长具有积极作用*Beck,Levin,Spare tire? Stock markets,banking crises,and economic recoveries.Financial Economics,2015(1).。
一、实证过程说明
(一)待检验假说
股票市场的快速发展可以有效改善企业的融资约束,提高企业融资效率使经济快速增长,同时,股票市场的诸多宏观经济效应也从不同的渠道影响企业和个人达到促进经济增长的目的。为此,对于股票市场与经济增长的关系问题,提出如下的假说1。
假说1 :股票市场发展成熟度高的国家能够更好地解决企业的融资约束,提高企业融资效率,并通过各种渠道促进经济增长。
另外,技术冲击、经济周期等不可观测因素也会对经济增长产生影响,并且可能与其他影响因素相关,如果遗漏会造成估计的偏误。本文考虑了这种因素,同时假定各个经济体对共同冲击的反应具有异质性。如2008年的全球经济冲击对于各国的影响是非对称的,冲击来源地美国受到的影响最深,其他国家和地区受到的影响按与美国经济的紧密程度呈现发散式递减的状态。为了刻画这种异质性影响,提出假说2。
假说2 :技术冲击、经济周期等共同冲击会对各国的经济增长产生影响,并且这种影响对于各个国家而言具有异质性。
(二)模型设定
为了检验假说,设定如下的面板模型 :
lnyit=αi+β′Xit+uit
(1)
其中,下标i和t分别表示地区和时间,ln表示取自然对数。lnyit表示各国的真实人均收入水平,而Xit表示影响真实人均收入水平的关键变量,主要包括衡量股票市场发展程度的变量以及其他影响人均收入的外生变量,而αi表示个体效应。伴随着全球经济一体化的提高,各经济体间“一荣俱荣、一损俱损”的现象逐渐变为现实,现实中的技术冲击、经济冲击等因素会同时影响各国经济,为了刻画这种空间强相关性所带来的潜在影响,设定了如下的包含共同因子的双向固定效应模型 :
(2)
(3)
(2)式中,技术冲击、经济周期等因素对地区收入水平的影响主要体现在变量ft上,由于周期性因素可能与其他解释变量相关(体现为(3)),如果遗漏了变量ft的影响,估计结果可能是有偏、不一致的。另外,从双向固定效应模型可见,技术冲击、经济周期因素对于各国人均收入水平的影响具有同质性(ft的系数对于任意个体而言均等于1),这种假设过于强烈并不符合实际,因此还借鉴Pesaran(2006)、Bai(2009)的做法,设定如下包含异质性共同因子影响的模型 :
(4)
(5)

(三)估计策略
对于以上三个计量模型,估计策略如下 :首先对基准模型和双向固定模型采用固定效应方法进行估计;而对于包含共同因子的CCEP模型,将(4)和(5)式进行合并,可以得到如下的式子 :
(6)
(7)
(8)
(9)
其中,Ik是k阶单位矩阵,而Ci是共同因子载荷系数矩阵的m×(k+1)矩阵,m是共同因子的个数,Pesaran(2006)建议使用解释变量和被解释变量的截面均值作为不可观测共同因子的代理变量,这可以通过如下的变换得到证明,对(6)式求均值可以得到 :
(10)

(11)
(12)
(13)

(14)
在(14)式的设定下,Pesaran(2006)证明可以得到参数αi、β1、β2、β3的一致估计,即 :
(15)
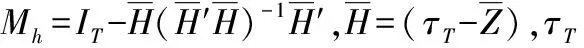
(四)数据说明
本文所涉及的数据来源于OECD数据库、世界银行数据库、国家统计局、wind数据库。样本包括我国和34个OECD国家,样本个数为35个。由于大多数国家股票市场完整数据起始于1992年而终于2012年,因此出于数据平衡性考虑,将样本的考察期定位为1992—2012年。最终获得了平衡的面板数据集(N=35,T=21)。
根据相关文献,将实际人均GDP水平作为本文的被解释变量,为了控制价格因素,采用2005年不变美元价格来计算实际人均GDP。对于解释变量,前人研究中关于影响经济增长的指标很多,出于数据的可得性及本文的研究目的,选择了如下指标。
(1)股票市场的交易额占GDP的比重(TST_GDP)(Atje和Jovanovic,1993;Levine和Zervos,1998);(2)股票交易换手率(TURN);(3)股票市场资本总额占GDP的比重(CST_GDP)。此外还选取两个可能影响经济增长的交叉因素;(4)政府对经济的干预程度(FIN_GDP),政府部门的态度会对经济增长产生重要影响,这种影响体现在自由主义与凯恩斯主义的争论之中,在此采用政府的财政支出占GDP的比重来度量政府对于经济的参与程度;(5)经济集聚度(N),近年来,随着新经济地理学的发展,经济在国家或者地区的集聚程度被认为是影响经济增长与发展的重要因素(Ciccone和Hall,1996;Mion,2009),采用每平方公里上的劳动力人数来度量经济的集聚程度。
下面的表1给出了本文所用的变量说明,而表2则给出了这些变量的统计描述。
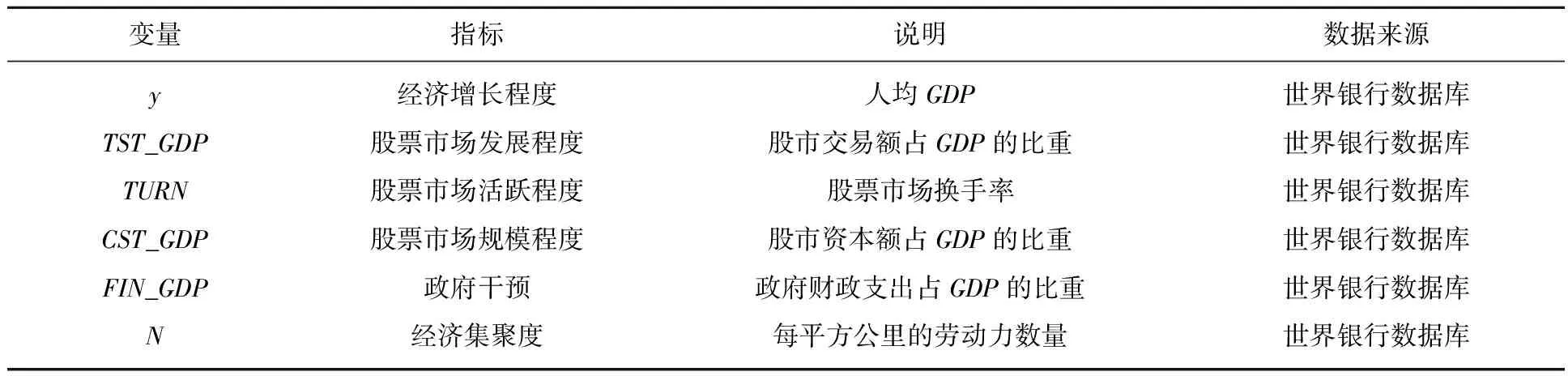
表1 模型主要变量指标说明
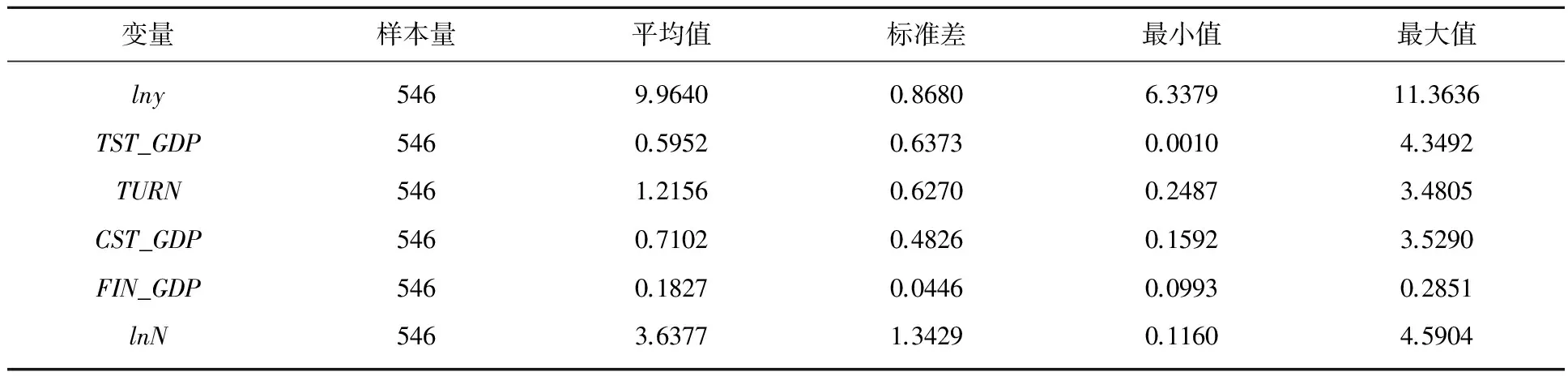
表2 模型主要变量的统计描述*ln表示自然对数。
二、实证结果分析
(一)变量的同期相关性检验
为了确定计量模型的合理性,即模型中的变量是否受到共同冲击的影响,同时为后文中的面板单位根检验提供依据,本节首先检验模型中的变量是否具有同期相关性。目前检验空间相关性的统计量主要有Moran’s I统计量(Moran,1948)、LM统计量(Breusch和Pagan,1980)、CD统计量(Pesaran,2004)。Moran’s I统计量依赖于先验设定的空间加权矩阵W,LM统计量适用于N
(16)

为了保持检验的稳健性,在是否包含趋势项的检验当中,都选取了变量的1-4阶滞后进行了检验发现,本文所涉及到的变量均存在同期相关性,这说明设定包含共同因子的空间计量模型是具有合理性的,也为后文单位根检验和模型估计提供了依据。

表3 模型变量空间相关性检验结果*“**”、“*”表示5%、10%以上的显著水平。以上CD统计量的计算分两个步骤完成 :(1)首先对每个个体i对应的变量进行p阶的ADF(p)检验,然后保存残差;(2)其次利用保存的残差根据上面的CD统计量的公式计算出CD数值。CD统计量渐近服从N(0,1)分布。ln表示自然对数。
(二)变量平稳性检验
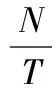
CIPS检验方法是在每个截面个体的ADF回归方程中添加滞后变量及其一阶差分项的截面均值来控制由共同因子所引起的截面同期相关性,即 :
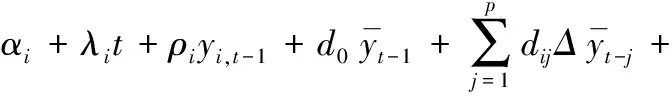
(17)
对于(17)式的回归,Pesaran(2007)对面板中的每个个体i进行回归,然后对回归滞后项yi,t-1系数的t统计量(简记为CADFi)求平均值,便可以得到CIPS统计量 :
(18)
Pesaran(2007)给出了各种N和T组合情况下K1、K2、CIPS统计量的临界值。CIPS检验的原假设为存在单位根,因此如果能拒绝原假设,那么变量是平稳的;而如果不能拒绝,说明变量是非平稳的。
表4给出了本文变量的CIPS单位根检验结果。由于数据时间长度的限制和节约自由度的目的,单位根检验选择了一阶滞后。从表可得,无论是否包含确定性线性趋势项,本文中所涉及变量的CIPS值是不显著的,也就是说变量都是非平稳的变量。随后对变量的一阶差分进行了单位根检验,发现至少在10%水平上显著,这说明变量经过一阶差分之后是平稳的,因此本文中所涉及的变量均是I(1)变量。

表4 CIPS单位根检验结果*注 :“**”、“*”表示5%、10%以上的显著水平。CIPS检验的原假设为存在单位根,由于时间长度的限制以及出于节约自由度的目的,在检验中选取了一阶滞后。Δ表示变量的一阶差分。CIPS检验5%临界值为-2.14(仅含截距)、-2.67(含截距和时间趋势),10%临界值为-2.07(仅含截距)、-2.58(含截距和时间趋势) 取自Pesaran(2007)。ln表示自然对数。
Pesaran(2006)最初在提出CCEP估计方法时只考虑共同因子本身为平稳变量的情形,但是Kapetanios、Pesaran和Yamagata(2011)的研究表明,如果共同因子为I(1)变量,CCEP的估计仍然是一致的。
(三)模型估计结果
在估计CCEP模型之前,为了进行模型选择和比较,首先估计POOL模型,结果见表5的第2列。随后,估计基准模型和双向固定效应模型。从表5中第3列和第4列可以看出,Hausman检验结果一致表明拒绝随机效应,且F统计量高度显著,说明模型中个体和时间效应共存。
但是在双向固定效应模型中,时间固定效应假设共同冲击对于各个经济体的影响具有同质性(即γi=1),这与现实不符,于是进行了CCEP估计,表中第5列给出了估计结果。为了比较CCEP模型与双向固定效应模型优劣,进行了Hausman检验。表5中第5列CCEP估计的Hausman统计量高度显著,说明经济冲击存在个体异质性,即CCEP模型相对于与双向固定效应模型是一个更优的模型。
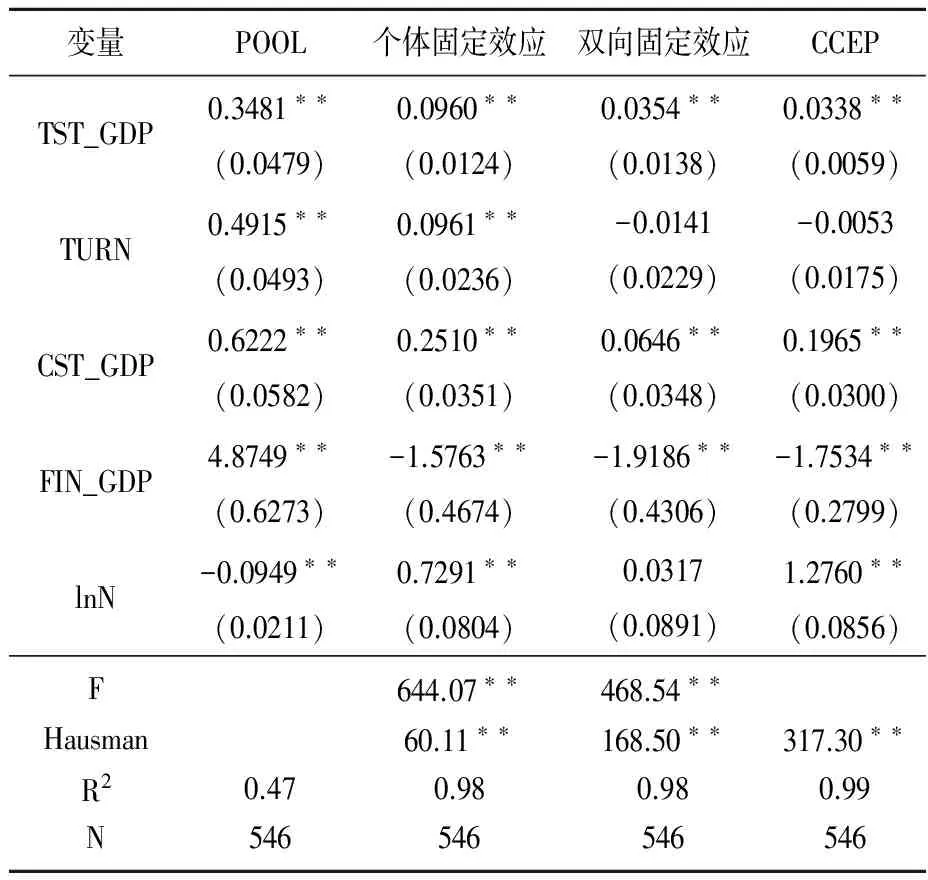
表5 模型估计结果及其比较*“**”和“*”分别表示在5%和10%以上的水平显著,括号之内的数字表示标准误。限于篇幅没有报告截距、个体效应和时间效应。F统计量用于检验个体或者时间效应的联合显著性。Hausman统计量用于选择固定效应或者随机效应。
从各个模型的估计结果看,无论是POOL模型、基准模型还是双向固定效应模型,其变量系数均有不合理之处,且hausman值较小,而CCEP模型的系数的估计值基本符合预期。具体而言,首先,重点关注的股票市场发展程度变量(TST_GDP)和股票市场规模程度变量(CST_GDP)的系数显著为正,即股票市场发展程度越高的国家,拥有更高的人均收入水平;其次,度量股票市场活跃程度的变量(TURN)在控制共同冲击因素后并不显著,一种解释是换手率不能直接体现股市发展情况,相反在一定程度上换手率过高还代表股市中短期投机行为盛行,不利于公司融资;最后,另外两个控制变量的系数估计结果也与理论预期基本一致,政府过度干预(FIN_GDP)经济,会影响经济配置资源的效率不利于经济的发展。经济集聚度(lnN)的提高可以发挥规模经济效益有利于经济增长。
(四)协整分析
在CCEP模型估计的基础之上,本节进一步检验实际人均收入(lny)、股票市场发展程度(TST_GDP)、股票市场换手率(TURN)、股票市场规模程度(CST_GDP)、政府干预(FIN_GDP)和经济集聚度(lnN)之间是否存在协整关系。根据前文的估计和检验,由于 CCEP模型回归中包含有共同因子的信息(空间强相关ft),所以依然采用CIPS的单位根检验方法。检验中设定只包含截距项,滞后阶数取1,检验得到的CIPS统计量为-2.4511,CIPS检验5%临界值为-2.14(仅含截距),因此,CCEP模型回归得到的残差是平稳的——即变量间存在着协整关系。
(五)共同因子分析
前文的结果证明了假说1——股票市场的发展能够促进经济增长,下面验证假说2——技术冲击、经济周期等共同冲击会对各国的经济增长产生具有异质性的影响,即分析空间强相关影响——共同因子ft和因子载荷系数γ′。由于CCEP模型的参数估计是一致的,首先利用CCEP模型得到的参数计算残差,计算的具体过程如下 :
(19)
(20)
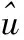
(21)
(22)
(23)
(24)
(25)
(26)
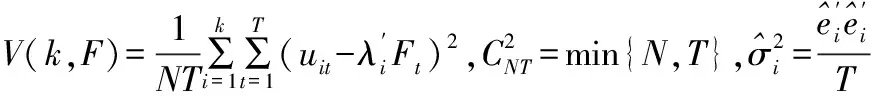
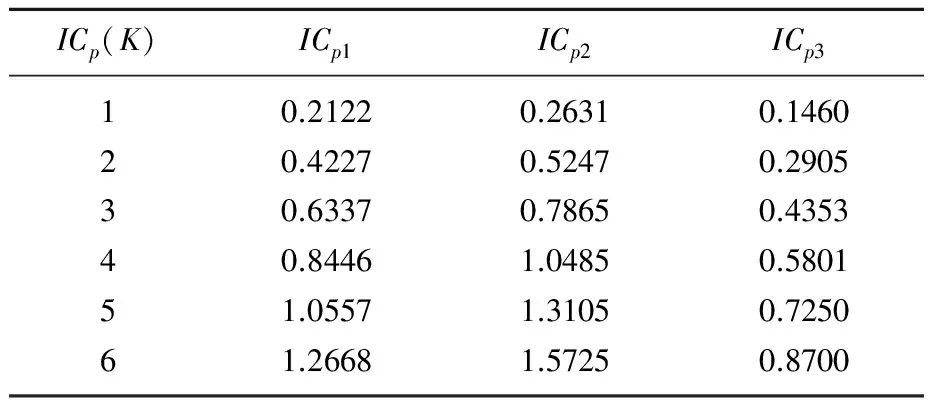
表6 共同因子IC准则判定结果*本表根据Bai和Ng(2002)的三个IC准则计算而得。
从表7共同因子的估计结果以及图1共同因子的时变特征可以发现其呈现出先上升后下降的趋势,并具有波动的特征。从其上升的趋势上看(1992—1999年),共同因子很可能反映了技术变革所带来的有利的共同冲击(如电脑的普及等),这种正向的技术冲击提高了生产效率。而当这种正向冲击在各个经济体传递时,会以一种强空间相关的方式导致各经济体的发展水平持续上涨。另外,共同因子也较好地刻画了几次经济危机的情况。如2001年的互联网泡沫经济危机、2007年的次贷危机以及2009年的欧债危机,这些不利的冲击对我国及OECD国家都产生了深远的影响,使得各国经济的发展都笼罩在一片阴霾当中,经济增长速度也出现不同程度的下滑。
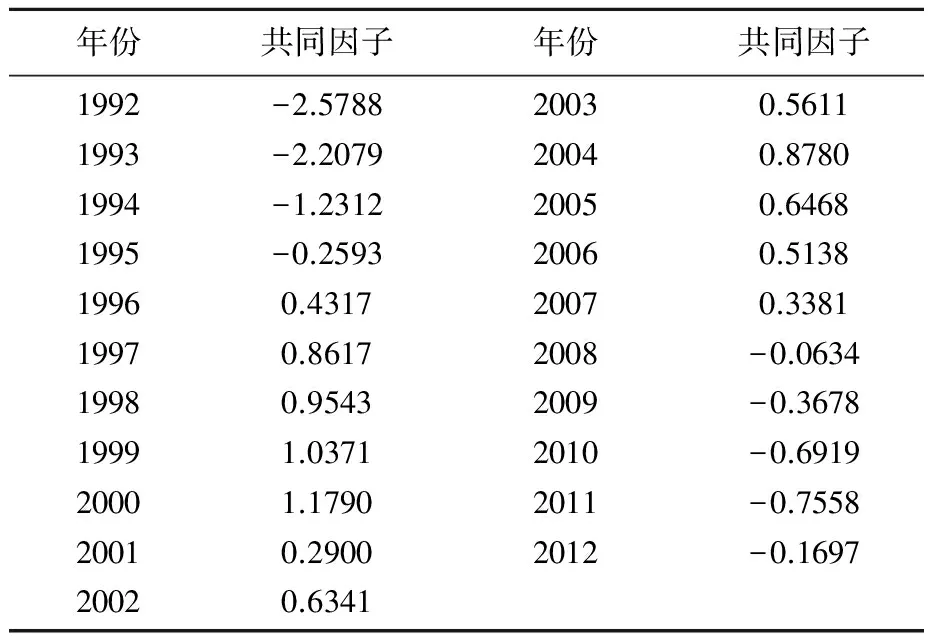
表7 共同因子的估计结果*共同因子根据Bai and Ng(2003)采用主成分方法进行估计。
最后,为了反映各国对于共同冲击的反应程度估计了各个因子的载荷系数。估计结果参见表8,首先,样本中的各个国家对于共同冲击的反应程度是不同的,这验证了假说2关于共同冲击的异质性特征。其次,虽然因子载荷系数各不相同,但都为正,这说明各个经济体对于技术冲击、经济周期因素的反应呈现出“顺周期”特征*即当因子载荷系数γi为正时,经济体对于共同冲击的反应会随着其增加而增长(注意反应程度为γi ft),随其减少而降低,因此呈现出顺周期特征;而当因子载荷系数为负时,经济体对于共同冲击的反应会随着其增加而降低,随其减少而增长,会表现出反周期特征。。再次,将35个国家划分为欧洲、美洲、亚洲、大洋洲四大区域发现,无论哪个区域,经济规模大的国家对于共同冲击的反应更为强烈,如欧洲的英国、德国、法国,美洲的美国和加拿大,亚洲的中国和日本,大洋洲的澳大利亚。

图1 共同因子时间变化图
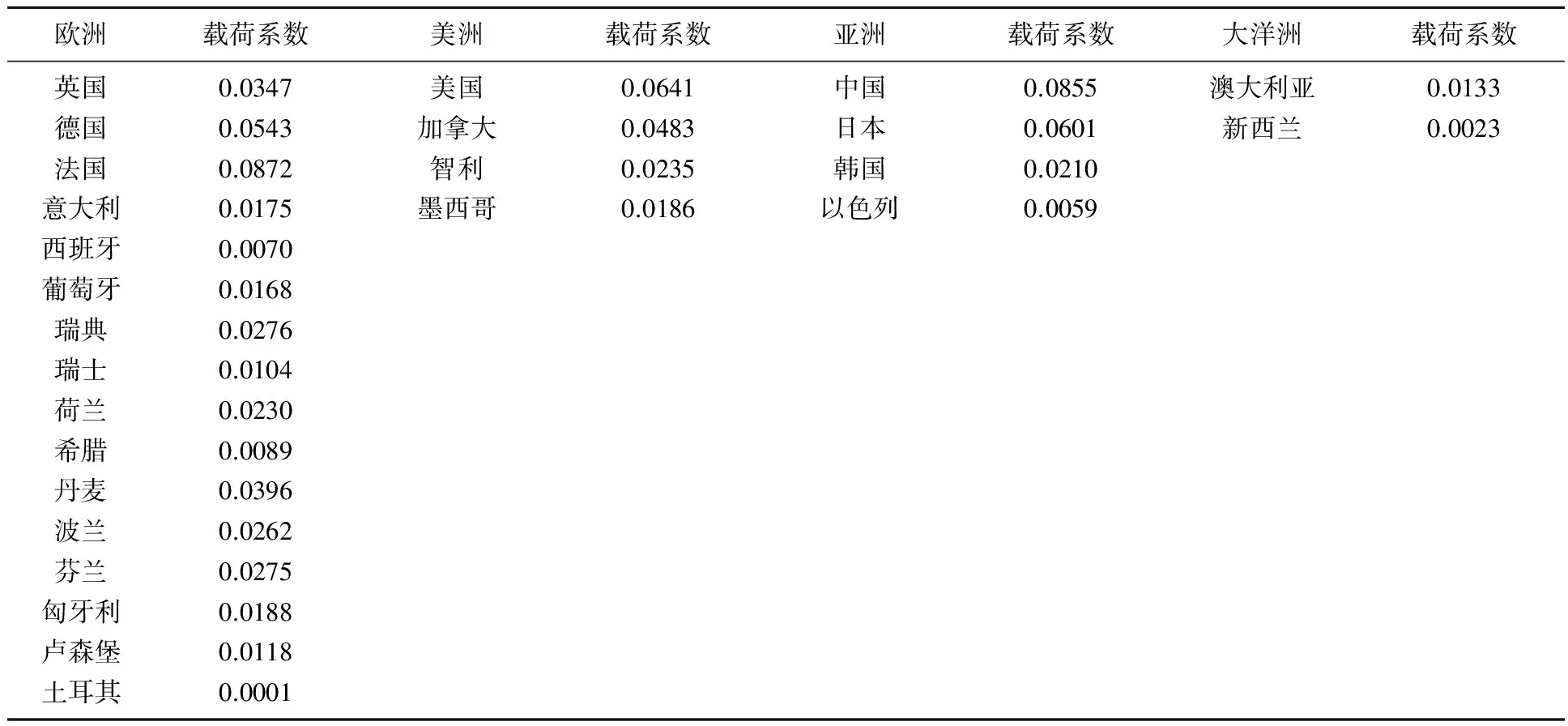
表8 OECD国家及中国因子载荷系数
三、结 论
本文基于1992—2012年35个国家的面板数据对股票市场与经济增长的关系进行了实证研究,在实证中主要发现以下几个结论 :
首先,发现实证所涉及的变量均为I(1)变量,在模型比较的基础上,采用CCEP方法得到参数的一致估计,发现股票市场的发展和经济集聚度对于各国的经济增长具有正向促进作用,股市换手率的影响并不显著,政府的过度干预会损害经济的效率从而不利于经济增长。
其次,发现实际人均收入、股市发展程度、股市换手率、股市规模程度、政府对经济的干预度、经济集聚度等变量存在长期协整关系,说明股票市场的发展对于经济增长的影响从长期来看是稳定的。
最后,借鉴Bai和Ng(2003)的ICp准则确定了共同冲击的个数,采用主成分分析方法提取了共同因子并估计了因子载荷系数,发现共同因子较好地刻画了技术冲击、经济周期因素等共同冲击对各个国家经济增长的影响。并且从因子载荷系数的估计中发现,经济体的经济规模越大,对于共同冲击的反应越强烈。
[责任编辑 :王 波]
本文为国家社会科学基金项目“财政支持新农保可持续发展问题研究”(项目编号:13BSH051)、教育部人文社科项目“资本认缴制及交易安全研究”的阶段性成果。
崔华泰,中国人民大学经济学院博士研究生。
F832.5
A
1003-8353(2016)011-0113-07
