R134a/R23复叠制冷系统级间容量比的优化分析

乔亦圆,杨东方,曹锋,黄振华

(1.西安交通大学能源与动力工程学院, 710049, 西安;2.浙江志高机械有限公司,324002,浙江衢州)



R134a/R23复叠制冷系统级间容量比的优化分析

乔亦圆1,杨东方1,曹锋1,黄振华2

(1.西安交通大学能源与动力工程学院, 710049, 西安;2.浙江志高机械有限公司,324002,浙江衢州)

为了提高复叠制冷系统的性能以及优化系统设计时各循环压缩机的匹配问题,提出了无量纲参数——级间容量比,即低温循环压缩机进口处的体积流量与高温循环压缩机进口处的体积流量之比。建立了复叠制冷系统的数学模型,分析了级间容量比对中间温度和系统性能系数(COP)的影响,并在蒸发温度为-75～-55 ℃、冷凝温度为20～50 ℃及复叠温差为5～13 ℃的各种工况下,探究了最优级间容量比与工况参数的关系。结果表明:若级间容量比增加,则中间温度增加,COP先增加后缓慢减小,存在使COP最大的最优级间容量比;工况温度对COP的影响大于级间容量比对COP的影响,随冷凝温度上升,最优级间容量增大,蒸发温度上升,最优级间容量比增大;复叠温差增大,最优级间容量比减小;冷凝温度、蒸发温度及复叠温差平均每上升10 ℃,最优级间容量比变化范围为0.1～0.2。由工况参数和最优级间容量比的计算结果拟合得到了优化关联式,其计算思路和结果分析可为实际设计中各循环压缩机排量的选型匹配提供理论依据。

复叠制冷系统;压缩机匹配;变工况分析;优化

随着人们对科技领域的探索和社会的进步,医疗、化工、航天等领域需要更低的制冷温度。目前应用最广的是压缩蒸汽制冷循环,单级压缩实现的压比不能过大,加上制冷剂本身物性受限,在蒸发温度很低时,只用一种制冷剂无法实现,故将总温差分割成多段,每段温度区间用合适的制冷剂,使得最低温度区的循环蒸发温度更低。

复叠系统可分为自复叠系统和传统复叠系统,自复叠系统利用混合制冷剂各组分的沸点不同,在不同温区内可实现制冷剂的分离和温度区间的复叠[1-2]。传统复叠系统的各组制冷剂独立,组成不同温区的循环,本文研究针对的是传统复叠系统。

国内外学者对复叠系统的研究集中于蒸发温度为-50 ℃左右的系统。文献[3]通过实验,对R404A/CO2复叠系统、R22制冷系统及R404A制冷系统进行对比,从系统COP、环保性、管路尺寸、压缩机等部件尺寸及压力控制等方面展开研究。文献[4]简化R134a/R410A复叠热泵系统模型,进行变工况数值模拟和实验探究。文献[5]研究了CO2/NH3复叠系统应用降膜式蒸发冷凝器的理论循环,研究了系统COP与3个换热器参数的关系。文献[6]对NH3/CO2复叠系统进行了不可逆损失分析。文献[7]通过实验比较了高、低温循环制冷剂均为R134a的复叠系统和R134a的单级循环系统,验证冷负荷和冷却水质量流量对复叠系统性能的影响。文献[8]从熵增的角度讨论最佳中间温度的影响因素,其中吸气过热和节流是熵增主要部分,二者对中间温度的影响不同,其中节流带来熵增的同时还造成中间温度的波动。然而,对于蒸发温度为-85～-65 ℃系统的研究较少,以易燃的烯烃及其混合工质等为主[9],尚未见到有关变工况性能及各循环压缩机匹配的研究。

本文对蒸发温度为-85～-65 ℃的复叠系统进行模拟,分析了级间容量比对系统性能的影响,并在不同蒸发温度、冷凝温度及复叠温差下,求得使COP最大的级间容量比,建立了最优级间容量比的关联式,为复叠系统优化设计提供了理论基础。

1 R134a/R23复叠制冷系统模型

1.1 热力学模型

本文研究蒸发温度为-75 ℃左右的复叠制冷系统,如图1所示。该系统由高温循环和低温循环组成,高温循环制冷剂为R134a,低温循环制冷剂为R23。中间换热器是高温循环的蒸发器和低温循环的冷凝器,两制冷剂间的传热温差称为复叠温差。

图1 复叠制冷系统流程图

图2表示该系统循环的T-s图和p-h图,各点均按实际热力学参数取值。低温循环压缩机吸气过热度为30 ℃,高温循环吸气过热度为10 ℃。以高温循环蒸发温度作为中间温度(To,h),低温循环冷凝温度即为中间温度与复叠温差之和。根据能量守恒和质量守恒原理,组成系统的各部件均看成控制容积[10]。为进行理论分析,做出如下假设:

(1)各部件都处于稳态,忽略因工质流动过程或振动动能造成的损失,以及中间换热器传热过程的能量损失;

(2)压缩过程中等熵效率取0.75;

(3)忽略蒸发器、冷凝器及连接管路等管道内的压降和热损失;

(4)高、低温循环的节流过程均为绝热节流。

(a)复叠循环T-s图

(b)复叠循环p-h图图2 R134a/R23复叠制冷循环图

设无量纲参数nV为两循环级间容量比,即低温循环压缩机进口处的体积流量Vl与高温循环压缩机进口处的体积流量Vh之比

nV=Vl/Vh

(1)

设高温循环质量流量mh=1 kg/s,且有

WH=mh(h6′-h5′)

(2)

WL=ml(h2′-h1′)

(3)

Qcas,H=mh(h5′-h8)

(4)

Qcas,L=ml(h2p-h3′)

(5)

Qo=ml(h1-h4)

(6)

式中:WH、WL为高、低温循环压缩过程耗功;h6′、h5′分别为高温循环压缩机出口、入口的比焓;h2′、h1′分别为低温循环压缩机出口、入口的比焓;Qcas,H、Qcas,L分别为高、低温循环在中间换热器内的换热量;h5′、h8分别为高温循环在中间换热器内出口、入口的比焓;h2p、h3分别为低温循环在中间换热器内出口、入口的比焓;Qo为复叠系统制冷量;h1′、h4分别为低温循环蒸发器出口、入口的比焓。

高低温循环在中间换热器内的换热量相同,可求得低温循环质量流量

(7)

将式(7)代入以上各式,可求得高、低温循环的性能系数rCOP,H、rCOP,L和系统rCOP如下

(8)

rCOP,L=Qo/WL

(9)

(10)

两循环体积流量Vl与Vh可由下式求得

Vl=ml/ρ1′

(11)

Vh=mh/ρ5′

(12)

式中:ρ5′、ρ1分别为高低温循环压缩机进口处制冷剂的密度。

1.2 数学模型

本文研究级间容量比对系统性能的影响,计算流程如图3所示。给定某一级间容量比,中间温度取值从低到高依次增加0.000 5 ℃,开始高温循环在中间换热器内制冷量小于低温循环在中间换热器内的制热量,当高温循环制冷量大于低温循环制热量时,认为此时中间温度为该级间容量比下的中间温度,进而可计算COP等参数。

图3 级间容量比对系统性能影响的计算流程

为了分析最优级间容量比与工况参数关系,选取不同工况参数和中间温度,求得系统最大COP及对应的最佳级间容量比,过程如图4所示。

图4 变工况下最优级间容量比的计算流程

2 级间容量比对系统的影响

2.1 对中间温度的影响

级间容量比对中间温度的影响如图5所示。在同一工况下,中间温度随级间容量比的增加而增加。这是由于高温循环质量流量mh=1 kg/s恒定,级间容量比增加时,若中间温度不变,高温循环吸气量恒定,则中间换热器内的换热量恒定。对低温循环,随级间容量比增加,压缩机吸气量增加且入口处制冷剂密度不变,质量流量增加,则中间换热器内换热量增加。高温循环为满足相同的换热量,应提高中间温度以增加高温循环的单位质量制冷量,因而高温循环压缩机入口处密度增加,吸气量减小。中间温度的上升虽使低温循环单位质量制热量减小,但因其质量流量增加更多,故能保证中间换热器内换热量与高温循环匹配。

由图5a还可看出,在同一级间容量比下,冷凝温度(Tk,h)越高,则中间温度越高。由于冷凝温度升高,高温循环在中间换热器内的换热量减小。当中间温度增加时,高温循环压缩机入口处制冷剂密度增加,压缩机吸气量减小,因而低温循环压缩机吸气量也减小,质量流量减小,且单位质量冷凝换热量也减小,故在中间换热器内的换热量减小直到与高温循环换热量相同。

由图5b可知,若蒸发温度(To,l)越低,则中间温度越低。这是因为,当蒸发温度下降时,低温循环压缩机入口处的密度下降,质量流量下降,中间换热器内制热量下降。为了减小高温循环在中间换热器内的制冷量,降低中间温度,此时两循环压缩机吸气量均增加,但比值不变。虽然低温循环在中间换热器中单位质量放热量增加,但由于其质量流量减小相对更甚,故中间换热器内换热量减小。

(a)冷凝温度变化

(b)蒸发温度变化

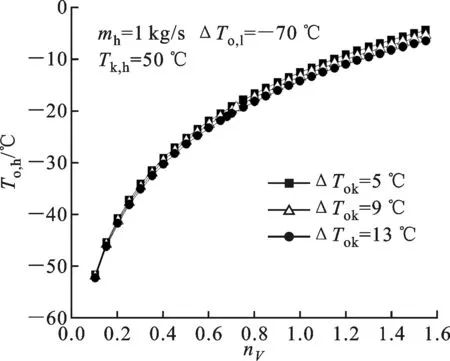
(c)复叠温差变化图5 不同工况下级间容量比对中间温度的影响

由图5c可知,当复叠温差(ΔTok)增大时,中间温度降低。复叠温差增加的幅度远大于中间温度下降的幅度,复叠温差每增加1 ℃,中间温度平均下降0.35 ℃,且级间容量比越大,复叠温差对中间温度的影响越明显。这是由于中间温度为高温循环的蒸发温度,复叠温差的增加意味着低温循环的冷凝温度增加,单位质量制热量减小,中间换热器内换热量减小,故降低中间温度使得高温循环单位质量制冷量减小。此时,高温循环压缩机入口处制冷剂密度减小,吸气量增加,低温循环压缩机吸气量同比例增加,质量流量增加幅度小于单位质量制热量的减小幅度,故中间换热器内换热量减小。

2.2 对COP的影响

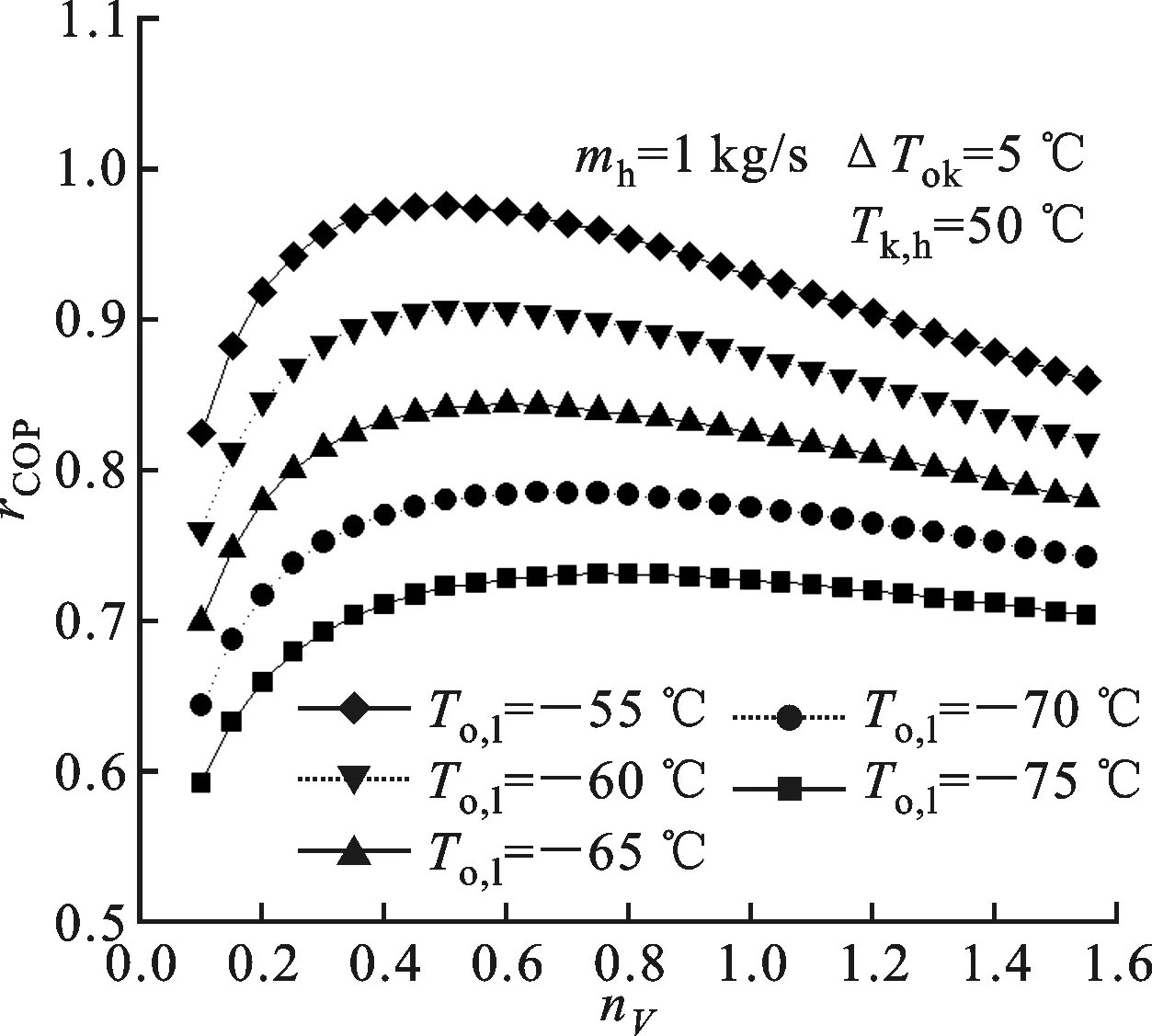
图6表示不同蒸发温度、冷凝温度和复叠温差下级间容量比对系统COP的影响。从图中可以看出,当级间容量比相同时,冷凝温度越高,蒸发温度越低,复叠温差越大,则系统COP减小。COP随级间容量比的增加先增加后减小,且减小速率小于增加速率。级间容量比对系统的影响可以看作是中间温度对系统的影响,二者正相关。由图6a可以看出,当COP最大时的最佳级间容量比随冷凝温度的增加而增加,由图5a可知,最佳级间容量比对应的最佳中间温度随冷凝温度的增加而增加。从图6b可以看出,COP取最大值时的最佳级间容量比随蒸发温度的上升而下降,最佳中间温度随着蒸发温度的上升而上升。图6c表示系统COP随复叠温差及级间容量比的变化情况,发现最佳级间容量比随复叠温差的减小而增加,最佳中间温度随复叠温差的减小而上升。

(a)冷凝温度变化

(b)蒸发温度变化

(c)复叠温差变化图6 不同工况下级间容量比对系统COP的影响

分析图6还可知道,工况温度对系统COP的影响大于级间容量比(或中间温度)对系统COP的影响。这是由于中间温度影响两循环压缩机入口处的制冷剂密度及在中间换热器中单位质量的换热量,中间温度上升,高温循环吸气量减小,则低温循环吸气量增大。中间温度同时改变高温循环和低温循环的吸气,故级间容量比(或中间温度)决定系统内部两循环的能量分配,及是否使系统性能达到最优。蒸发温度、冷凝温度及复叠温差决定系统所要克服的温差和叠加部分温差,这些因素对系统COP的影响要大于能量分配对COP的影响。

在不同工况下,系统存在最大COP和对应最佳级间容量比。工况参数和级间容量比两个因素引起系统COP的变化如图7所示。在不同工况下,选取合适的级间容量比可提高系统性能。

3 最优级间容量比分析及公式拟合

3.1 最优级间容量比的分析

按图4的计算流程求得使COP最大的最优级间容量比(nV,opt),图8表示了最优级间容量比与温度工况的关系。如图8a所示,冷凝温度上升时,最优中间温度和最优级间容量均提高。冷凝温度每上升约10 ℃,最优中间温度上升约1 ℃,最优级间容量比增大约0.11。中间温度提高意味着高温循环蒸发温度上升,压缩机吸气量减小,而冷凝温度上升幅度更大,故单位质量制冷量减小,在中间换热器内制冷量减小。低温循环单位质量制热量减小,且减小幅度小于在中间换热器内的制热量,故质量流量减小,压缩机吸气量减小且减小幅度小于高温循环,故最佳级间容量比增大。

从图8b可以看出,蒸发温度上升,最优级间容量比增大,同理最优中间温度升高。蒸发温度每上升约10 ℃,最优中间温度上升约4.5 ℃,最优级间容量比减小约0.18。对高温循环而言,蒸发温度上升而冷凝温度不变,单位质量制冷量和制冷量增加,压缩机入口处制冷剂密度增加且吸气量减小。对于低温循环,蒸发温度和冷凝温度均上升,且前者幅度更大,单位质量制热量减小,在满足中间换热器内制热量增加的前提下,质量流量增加,而压缩机入口处密度增加更剧烈,故吸气量减小。低温循环吸气量相对于高温循环吸气量减小幅度更大,故最优级间容量比减小。

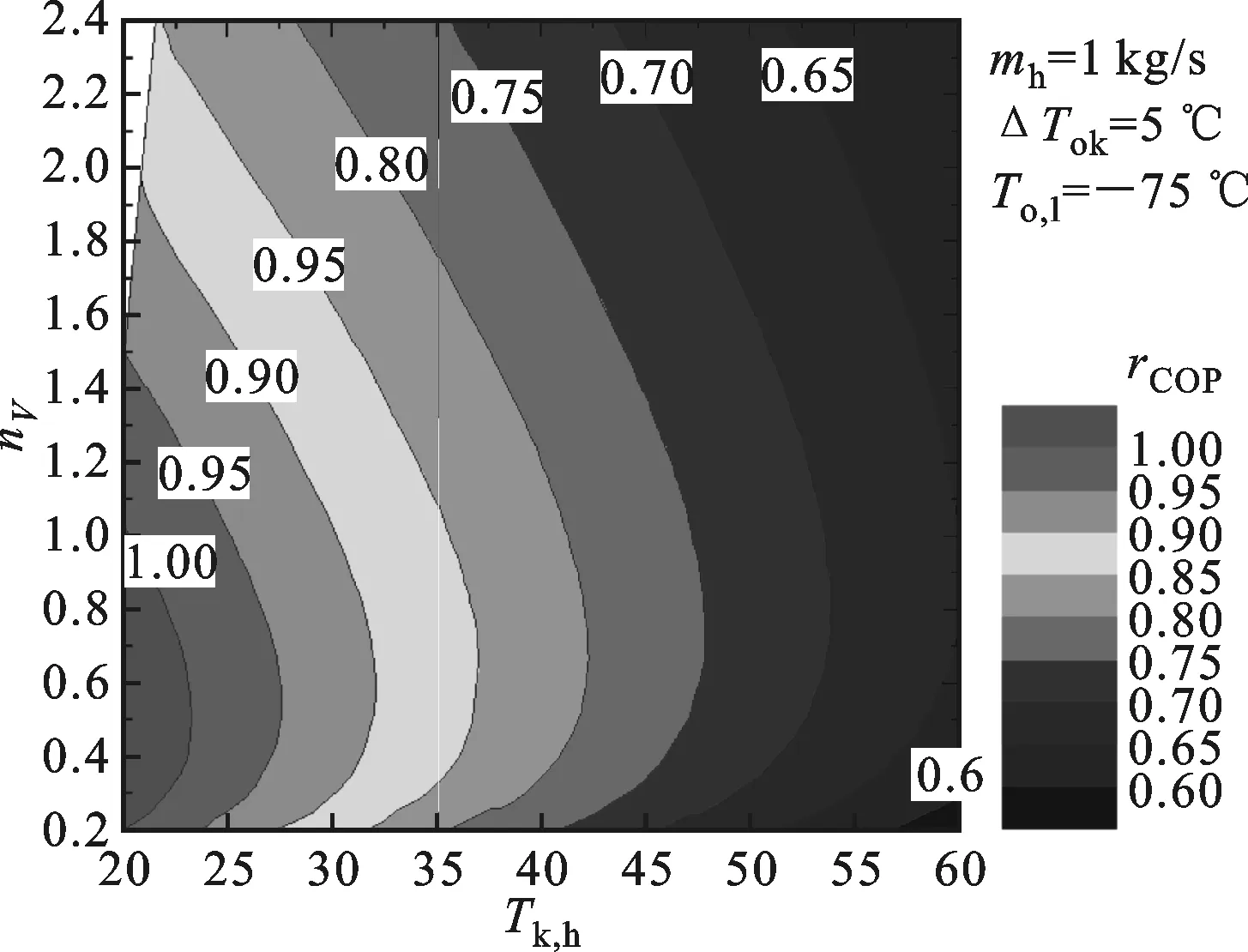
(a)冷凝温度和级间容量比

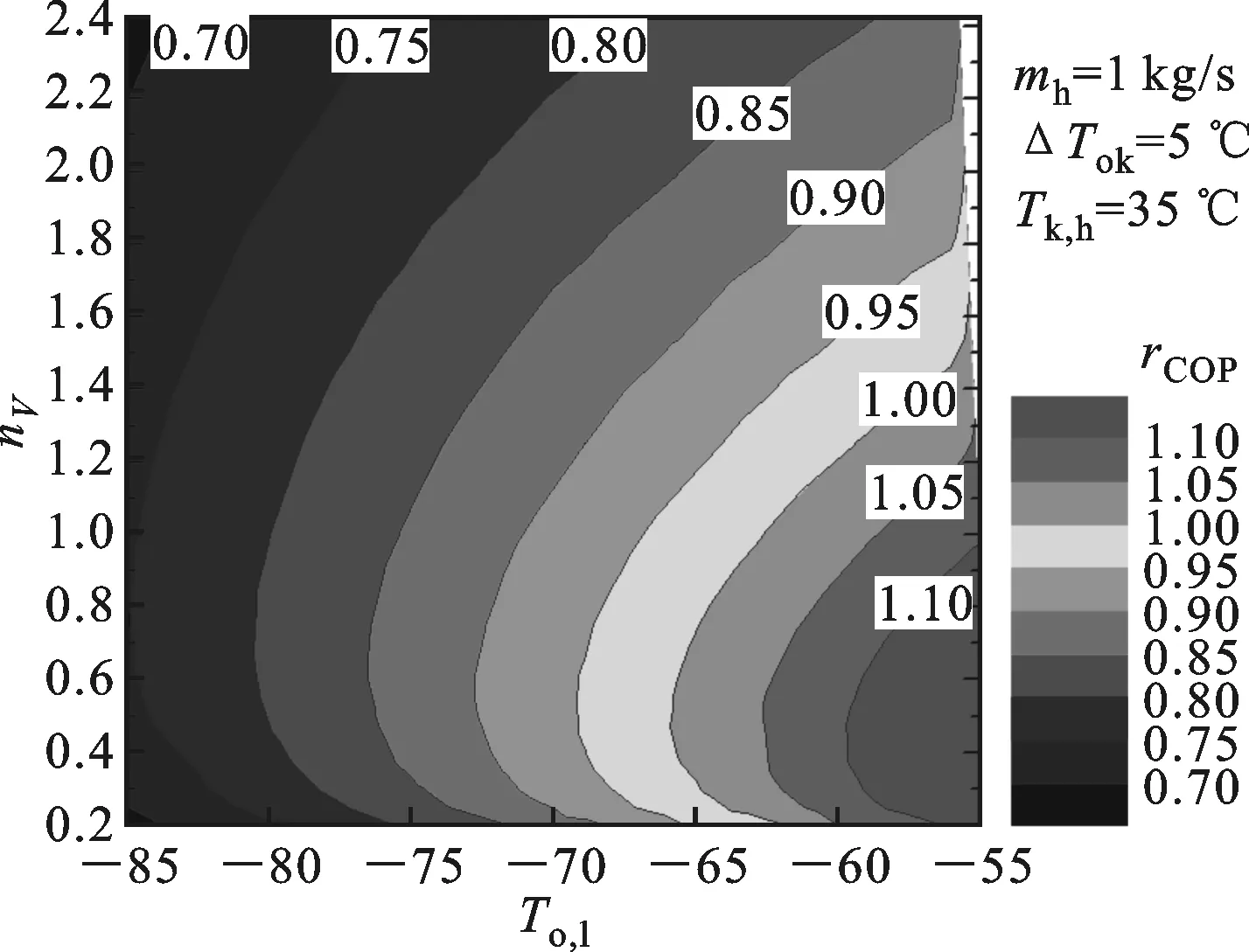
(b)蒸发温度和级间容量比

(c)复叠温差和级间容量比图7 工况参数和级间容量比双重因素引起系统COP的变化

(a)最优级间容量比与复叠温差的关系

(b)最优级间容量比与蒸发温度的关系

如图8c所示,最优级间容量比随复叠温差增大而减小。复叠温度每上升约10 ℃,最优中间温度下降约5 ℃,最优级间容量比减小约0.13。这是由于最优级间容量比对应循环最优中间温度,高温循环单位质量制冷量和中间换热器内制冷量减小,压缩机入口处制冷剂密度减小,吸气量增加。在低温循环中,虽然中间换热器换热量减小,但单位质量冷凝换热量减小幅度更大,故质量流量小幅度增加,且压缩机入口处制冷剂密度减小,吸气量增加。由于高温循环压缩机吸气量增加幅度大于低温循环,故最优级间容量比下降。

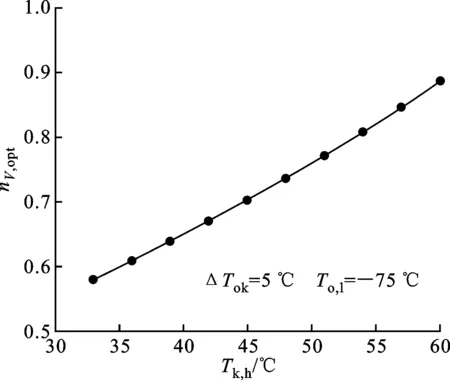
(c)最优级间容量比与冷凝温度的关系图8 最优级间容量比与各温度工况的关系

3.2 最优级间容量比的关联式拟合

基于以上最优值与温度工况的关系曲线,对最优级间容量比进行拟合,建立如下关联式

nV,opt=0.213+0.011Tk,h

(13)

(14)

nV,opt=0.829-0.012ΔTok

(15)

式(13)适用于33 ℃≤Tk,h≤60 ℃、To,l=-75 ℃、ΔTok=5 ℃的情况;式(14)适用于-85 ℃≤To,l≤-58 ℃、Tk,h=50 ℃、ΔTok=5 ℃的情况;式(15)适用于3 ℃≤ΔTok≤12 ℃、Tk,h=50 ℃、To,l=-75 ℃的情况。

在实际复叠系统设计选型时,最优级间容量比nV,opt为最优的低温循环与高温循环压缩机排气量之比,压缩机排量匹配可参考以上关联式。蒸发温度、冷凝温度及复叠温差的选取与实际换热器面积大小、换热方式强弱及循环整体温差有关。该组关联式及其计算分析思路可作为设计生产的参考依据。

4 结 论

本文针对复叠系统现今研究存在的不足,建立了数学模型和热力学模型,探究了级间容量比对系统性能的影响,并求得了各工况下最优级间容量比的拟合关联式,得出的主要结论如下。

(1)在某一工况下,中间温度随级间容量比的增加而增加。当级间容量比相同时,蒸发温度越高,中间温度越高;冷凝温度越高,中间温度越高;复叠温差越大,中间温度越低。

(2)当工况温度改变时,如蒸发温度越低,冷凝温度越高,复叠温差越大,则系统COP越小。级间容量比增大,系统COP呈先增加后缓慢减小的趋势。工况温度对系统COP的影响大于级间容量比(或中间温度)对系统COP的影响。

(3)在不同工况下,存在最大COP和对应最佳级间容量比。冷凝温度上升,最优级间容量增大;蒸发温度上升,最优级间容量比增大;复叠温差增大,最优级间容量比减小。拟合得到最优级间容量比的计算关联使式,在系统优化时,应选用最优或者稍大的级间容量比。

值得指出的是,本文只针对复叠制冷系统的级间容量比,探究其对系统性能的影响及在工况变化时的最优化问题,未涉及机组其他因素引起的性能变化。但重要的是,本文率先提出了级间容量比这一无量纲参数,弥补了复叠系统的研究空白,这更是实际生产设计中各级循环压缩机排量匹配的关键。级间容量比的计算过程和分析结果对理论研究和生产优化都非常有意义。

[1] 赖芬, 吴裕远, 欧阳前武, 等. 新型部分自复叠热泵的理论研究 [J]. 西安交通大学学报, 2012, 46(3): 15-20. LAI Fen, WU Yuyuan, OUYANG Qianwu, et al. Theoretical research on a new partial auto-cascade heat pump [J]. Journal of Xi’an Jiaotong University, 2012, 46(3): 15-20.

[2] 颜俊, 任挪颖, 钱伟, 等. R600a/CO2一级分凝和二级分凝自复叠制冷循环的性能研究 [J]. 西安交通大学学报, 2007, 41(3): 321-325.

YAN Jun, Ren Nuoying, QIAN Wei, et al. Performance study on R600a/CO2auto-cascade refrigerating cycle with one-step dephlegmation and two-step dephlegmation [J]. Journal of Xi’an Jiaotong University, 2007, 41(3): 321-325.

[3] DA SILVA A, BANDARRA FILHO E P, ANTUNES A H P. Comparison of a R744 cascade refrigeration system with R404A and R22 conventional systems for supermarkets [J]. Applied Thermal Engineering, 2012, 41: 30-35.

[4] PARK H, KIM D H, KIM M S. Thermodynamic analysis of optimal intermediate temperatures in R134a-R410A cascade refrigeration systems and its experimental verification [J]. Applied Thermal Engineering, 2013, 54(1): 319-327.

[5] MA Ming, YU Jianlin, WANG Xiao. Performance evaluation and optimal configuration analysis of a CO2/NH3cascade refrigeration system with falling film evaporator-condenser [J]. Energy Conversion and Management, 2014, 79(1): 224-231.

[6] ALBERTO DOPAZO J, FERNNDEZ-SEARA J, SIERES J, et al. Theoretical analysis of a CO2-NH3cascade refrigeration system for cooling applications at low temperatures [J]. Applied Thermal Engineering, 2009, 29(8): 1577-1583.

[7] KILICARSLAN A. An experimental investigation of a different type vapor compression cascade refrigeration system [J]. Applied Thermal Engineering, 2004, 24(17): 2611-2626.

[8] RATTS E B, BROWN J S. A generalized analysis for cascading single fluid vapor compression refrigeration cycles using an entropy generation minimization method [J]. International Journal of Refrigeration, 2000, 23(5): 353-365.

[9] MAFI M, NAEYNIAN S M, AMIDPOUR M. Exergy analysis of multistage cascade low temperature refrigeration systems used in olefin plants [J]. International Journal of Refrigeration, 2009, 32(2): 279-294.

[10]赖艳华, 董震, 邵长波, 等. R404A/CO2复叠式制冷系统的热力学分析与优化 [J]. 山东大学学报: 工学版, 2011, 41(2): 149-153. LAI Yanhua, DONG Zhen, SHAO Changbo, et al. Thermodynamic analysis and optimization of R404A/CO2cascade refrigeration system [J]. Journal of Shandong University: Engineering Science, 2011, 41(2): 149-153.

(编辑 杜秀杰)

Optimization of Compressors Displacement Ratio in R134a/R23 Cascade Refrigeration System

QIAO Yiyuan1,YANG Dongfang1,CAO Feng1,HUANG Zhenhua2

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. Zhejiang Zhigao Machinery Co. Ltd., Quzhou, Zhejiang 324002, Chian)

A dimensionless parameter, the compressor displacement ratio, is proposed to investigate the performance of the R134a/R23 cascade system and optimize the match of compressors of the system. The parameter is defined as the ratio of the compressor inlet volume flow rates between the low temperature cycle and the high temperature cycle. A numerical model is established to analyze the effect of the displacement ratio on the COP and the intermediate temperature. The relationship between the optimal displacement ratio and the operating parameters is discussed under various conditions when the evaporating temperature, condensing temperature and cascade temperature difference are ranged within -75～-55 ℃, 20～50 ℃ and 5～13 ℃, respectively. The results show that the intermediate temperature increases with the displacement ratio, while the COP rises first and then drops slowly. The variation of the operating temperature exerts a stronger impact on the COP than the displacement ratio. The optimal displacement ratio increases with the condensing temperature and the evaporation temperature, and decreases when the cascade temperature difference rises. The correlations of the optimal displacement ratio are obtained by fitting data of the working condition parameters and the optimum compressor displacement ratio.

cascade refrigeration system; compressor match; off-design condition analysis; optimization

2015-05-18。

乔亦圆(1991—),女,硕士生;曹锋(通信作者),男,教授,博士生导师。

时间:2015-11-11

10.7652/xjtuxb201602018

TB61

A

0253-987X(2016)02-0104-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151111.1809.004.html