采用博弈论的认知无线网络主用户和不可信任次用户的协作策略

马亚燕,王保云

(南京邮电大学通信与信息工程学院, 210003, 南京)



采用博弈论的认知无线网络主用户和不可信任次用户的协作策略

马亚燕,王保云

(南京邮电大学通信与信息工程学院, 210003, 南京)

针对认知无线网络中不可信任的次用户发送者(ST)会对主链路进行窃听的问题,以将主用户发送者(PT)和ST之间的敌对关系转化为协作关系为目的,提出2种采用博弈论的协作策略:斯塔伯格策略及其改进策略——双层博弈策略。在斯塔伯格策略中,ST工作于半双工模式,和窃听相比,它更希望传送数据,因此PT轮流和每个ST进行斯塔伯格博弈,选择对未被选中的ST(即潜在的窃听者)产生更多干扰的ST一起使用授权频段发送数据。为促进ST之间的竞争,将斯塔伯格策略扩展为双层博弈策略,外层仍是斯塔伯格策略,PT将所有的ST看作一个整体进行博弈;内层拍卖博弈中,每个ST尽可能提高安全速率来赢得接入授权频段的机会,PT则选择能提供最高安全速率的ST进行合作,因此它能够获得更高的收益。仿真结果表明,在这2种策略作用下,主链路的安全速率分别提高了63%和68%,ST接入授权频段的概率分别为56%和71%。

认知无线网络;博弈论;合作;安全

随着无线通信业务需求的爆炸式增长,频谱资源匮乏的问题变得日益严重。认知无线电技术允许次用户在不影响其他授权主用户正常通信的前提下复用稀缺的频谱资源,因此与传统的固定频谱分配方式相比提高了系统的频谱效率[1]。然而,由于无线信道的广播特性,认知无线电技术在提高频谱利用率同时也面临着严重的通信安全问题[2]。文献[3-5]从节点间协作的角度对如何提高认知无线电系统中主用户间通信安全进行了研究。现有协作策略大致可分为友好干扰[3]、合作中继[4]以及友好干扰与合作中继相结合[5]3类。

在认知无线网络中,如果次用户是不可信任的,即部分次用户节点会对主链路的通信进行窃听,那么主用户和次用户之间的合作会变得异常复杂[6-7]。文献[7]中次用户发送者(ST)工作于半双工模式,只有在主用户发送者(PT)允许它们使用授权频段发送数据时,才不会对主链路的数据进行窃听。Karim Khalil提出了有效的使用斯坦格尔伯格博弈的安全协作策略[7],PT选择一个合适的ST和它一起发送数据,该ST对未被选中的ST(即潜在的窃听者)产生较多的干扰,从而增强了主链路的安全性。虽然此协作策略是有效的,但是该策略中ST只能在被PT选中后决定是否接入授权频段进行传输,因此没有激发起ST之间的竞争;其次该策略不允许PT和ST调整自己的发送功率,因此会错失部分合作机会,即使合作也不能以最佳功率传输数据,在一定程度上损失了部分性能。

为此,本文首先给出了PT和ST协作的充分必要条件;然后,在文献[7]的基础上提出了采用斯塔伯格博弈的协作策略,并求出了相应博弈的纳什均衡点。与文献[7]中协作策略不同的是,本文所提出的斯塔伯格策略中PT的行动是选择合适的发送功率以及合适的ST进行合作,ST的行动是选择合适的发送功率以及被PT选中后是否接入授权频段进行传输。为了激发ST之间的竞争性,采用第二密封拍卖博弈[8]来模拟它们之间的相互作用,将该博弈作为上一步斯塔伯格博弈的子博弈,形成基于双层博弈的协作策略,并得出内层第二价格密封拍卖博弈的占优均衡以及外层斯塔伯格博弈的纳什均衡。仿真结果表明,本文所提2种协作策略均可明显提高主链路的安全速率和ST接入授权频段的机会。

1 系统模型

考虑如图1所示的认知无线电模型,包括1对主用户和2对次用户:PT拥有授权频道的使用权,需要将数据安全地发送给相应的接收者;2个ST都工作于半双工模式,希望借助于授权频段发送数据给各自的接收者,它们在空闲时隙能够感知到授权频段并接受PT的信息(即窃听),以此威胁PT允许它们使用授权频道发送数据。如果PT允许其中一个ST接入授权频段,另一个ST依然选择窃听;当被选中的ST发送的数据对主用户接收者(primary receiver, PR)产生的干扰小于对另一个ST产生的干扰时,主链路的安全性得以增强;被选中的ST也可借助于授权频段发送数据,和PT由敌人转化为朋友。因此,对PT而言,所有的ST既是潜在的敌人,也是潜在的朋友。

图1 系统模型

各链路的信道参数设置如下:主用户对之间的瞬时功率复增益为hm,次用户对之间的瞬时功率复增益分别为hs1、hs2(类似地,可以定义如图1所示的其他信道参数hw1、hw2、h21、h12、hi1、hi2、h1r、h2r);PT和ST的发送功率分别为Pp和Psi,它们的最大发送功率为Pmax;假设所有链路的噪声功率均为σ2。

2 斯塔伯格策略

假设所有节点是理性和自私的,则可以用博弈论来研究这类节点的相互作用[9]。因为PT在接入授权频段时具有更高的优先权,所以本节使用斯塔伯格博弈[8-10]来分析PT和ST之间的相互作用,其中PT和ST分别是领导者和跟随者,前者的行动是选择发送功率Pp以及选择合适的ST进行合作,后者的行动是选择发送功率Psi;博弈进行时,PT先行动,随后每个ST作出最佳反应来最大化各自的效用函数。

2.1 效用函数

假设STi被选中,定义

j∈{1,2},j≠i

(1)

则STj是主链路的窃听者。

PT的效用函数是主链路的可达安全速率;假设它选中STi一起传输数据,则主链路的可达安全速率为

(2)

式中:j如式(1)所定义;[x]+=max(x,0)。

被选中STi的效用函数为

(3)

式中:csi是STi的单位传输功耗。

当2个ST都选择窃听时,主链路的可达安全速率为

(4)

2.2 协作条件

为了更好地分析PT和ST之间的相互作用,首先分析它们效用函数的性质。

证明 参见附录A。

(5)

(6)

max(-B(i,j)/2A(i,j),0);Dsi>0

(7)

i=k,Dsi>0;C(i,j)>0;B(i,j)>0

(8)

2.3 斯塔伯格纳什均衡

(9)

(10)

从定义1可以看出,PT和ST在纳什均衡点的行动是对对方行动的最佳反应,可以根据后向分析法[8]来求解该均衡。

给定PT的发送功率Pp,STi的最佳发送功率是如下优化问题的解

(11)

因此,被选中STi的最佳发送功率为

(12)

PT的最佳发送功率是如下优化问题的解

s.t. 0≤Pp≤Pmax

(13)

因此,等式(12)和(13)给出了斯塔伯格博弈的均衡解。

2.4 胜出者的确定

首先PT轮流和2个ST进行斯坦格尔伯格博弈,接着选出能够给它提供最大安全速率的ST进行合作。被选中ST的序号为

(14)

3 双层博弈策略

3.1 双层博弈的基本概念

与文献[7]相比,上节提出的方案给予了PT和ST更多的主导权,但是它没有激发起ST之间的竞争,因此,这里采用双层博弈来模拟PT和多个ST之间的相互作用,其中内层采用拍卖博弈研究ST之间的竞争;外层仍采用第2节所描述的斯塔伯格博弈来研究PT和多个ST之间的相互作用,领导者仍然是PT,跟随者则由单个ST变更为所有的ST;内层拍卖博弈中胜出的ST的最佳发送功率选择,恰好是外层斯塔伯格博弈中它对PT发送功率的最佳反应。

3.2 第二价格密封拍卖

在现有的多种拍卖策略中,第二价格密封拍卖能够保护竞拍者的隐私,胜出的竞拍者只需支付给拍卖者所有报价中的第二高报价,每个竞拍者的最优行动是按照它对标的的完全估价进行报价,该行动恰好是博弈理论中的占优均衡[8]。

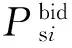
(15)

(16)

如果ST被PT选中,其效用函数如式(3)所定义。

3.3 占优均衡

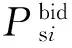
(17)

该优化问题的解如定理2所述。

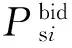
(18)

式中:Psi(1)由定理1给定。当不等式(8)满足时,次用户发送者i的占优行动为

(19)

证明 参见附录B。

说明2 因为本文采用的是第二价格密封拍卖,如果竞拍功率为零的ST赢得了拍卖,它只需提供第二高报价的安全速率,所以能够以大于0的发送功率传输数据。

3.4 胜出者的最佳功率选择

定理3 胜出次用户发送者v的最佳发送功率为

(20)

证明 参见附录C。

3.5 斯塔伯格纳什均衡

式(20)给出的结果是外层斯塔伯格博弈中ST对PT的功率选择Pp的最佳反映,因此和第2节类似,采用后向分析法求出PT的最佳发送功率为

s.t. 0≤Pp≤Pmax

(21)

式(20)和(21)构成了外层斯塔伯格博弈的纳什均衡。

说明3 虽然本文的系统模型只有2个ST,但是本文提出的这2种博弈策略均可以应用于有3个以上ST的情形,限于篇幅问题,这里不再详细叙述。

4 算法复杂度分析

本文涉及的算法复杂度包括信令/反馈复杂度以及计算复杂度。

在实际的认知无线电系统中,发送者一般利用复杂度较低的信道训练、估计和反馈机制来获得到相应接收者的信道增益[11],每个信道增益对应2个实数。计算安全速率时,需要获取的信道增益为hm、hwj、hir以及hij,假设系统中有N对次用户,则需要4N2+2N+2个实数的反馈开销(如hm由PR估计后反馈给PT,需要2个实数的反馈开销;hir由PR反馈给STi,再进一步反馈给PT,需要4个实数的反馈开销);类似地,计算ST效用函数时,需要6N个实数的反馈开销。另外,本文只需局部系统信道增益,所以信令/反馈复杂度可控。

对于计算复杂度而言,本文所提的斯塔伯格策略中PT轮流和N个ST进行斯塔伯格博弈,求出斯塔伯格纳什均衡,选出能够给它提供最大安全速率的ST进行合作,因此计算复杂度主要集中在纳什均衡的求解(式(12)和(13))。同理,本文所提的双层博弈策略计算复杂度主要集中在N个ST的轮流报价(式(18)),因此本文所提2种策略的计算复杂度均为O(N)。

综上,本文所提策略的算法复杂度较低,方案可行度较高。

5 仿真实验

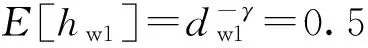
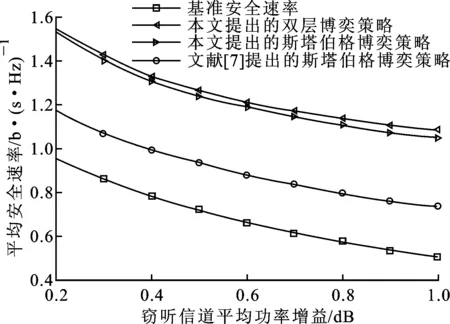
图2 3种策略下的平均安全速率随窃听信道平均功率增益的变化情况

图3为在上述3种策略下ST的平均效用函数随着E[hw2]的变化情况。从图3可以看出:这3种策略均能提高ST的性能;与文献[7]提出的斯塔伯格策略相比,本文所提出的双层博弈策略和斯塔伯格策略将ST的效用函数平均值分别提高了约190%和130%。

图3 3种策略下ST效用函数随着窃听信道平均功率增益的变化情况

图4为在上述3种协作策略下PT单独传输的概率随着E[hw2]的变化情况。当PT没有选中任何一个ST进行合作时,它将单独传输数据。从图4可以看出:E[hw2]=0.2时,在双层博弈策略的作用下,ST接入授权频段的概率高达71%;在本文和文献[7]所提出的斯塔伯格策略作用下,ST接入授权频段的概率分别为56%和30%,因此双层博弈策略更好地促进了PT和ST之间的合作,本文提出的斯塔伯格策略次之。

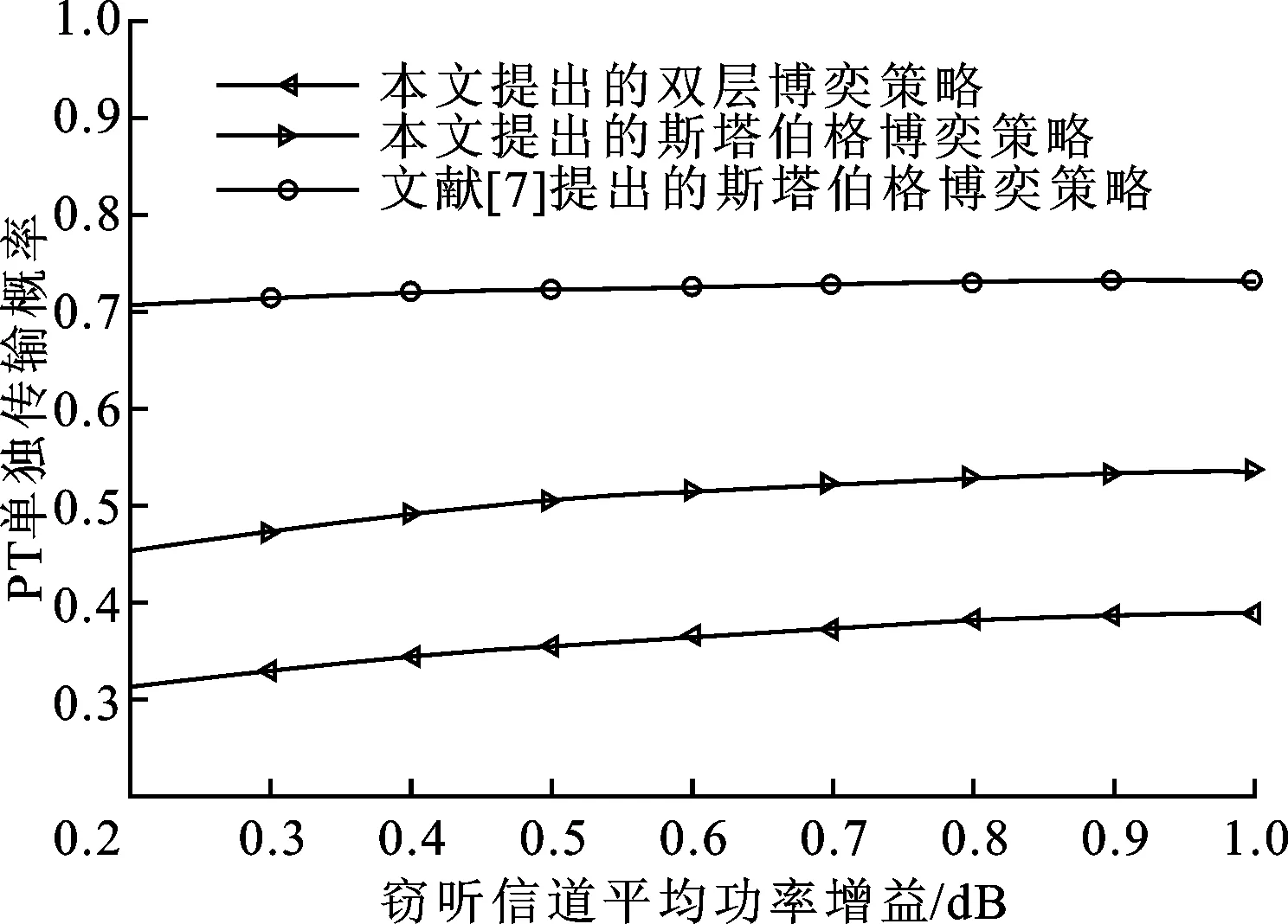
图4 PT单独传输概率随着平均功率增益的变化情况

6 小 结

本文采用博弈论研究认知无线电中PT和不可信任ST之间的合作。首先,通过分析PT和ST的效用函数性质得出它们之间合作的前提条件,然后为促进它们之间的合作,提出了采用斯塔伯格博弈的策略,并求出了相应的纳什均衡。为进一步激发ST的理性和自私性,将上述斯塔伯格策略扩展为双层博弈策略,外层仍采用斯塔伯格模型,内层采用改进的第二价格密封拍卖博弈来模拟次用户之间的竞争,得到了内层拍卖博弈的占优均衡以及外层斯塔伯格博弈的纳什均衡。仿真结果表明,本文提出的2种协作策略将主链路的安全速率分别提高了约63%和68%,次用户接入授权频段的机会分别为71%和56%。

[1] GOLDSMITH A, JAFAR S A, MARIC I, et al. Breaking spectrum gridlock with cognitive radios: an information theoretic perspective [J]. Proceedings of the IEEE Cognitive Radio, 2009, 97(5): 894-914.

[2] 裴庆祺, 李红宁, 赵弘洋, 等. 认知无线电网络安全综述 [J]. 通信学报, 2012, 34(1): 144-158. PEI Qingqi, LI Hongning, ZHAO Hongyang, et al. Security in cognitive radio networks [J]. Journal on Communications, 2012, 34(1): 144-158.

[3] KARIM K, EYLEM E. Achieving physical-layer secrecy via friendly jamming with dynamic role assignment for coordinating transmitters [C]∥IEEE Wireless Communications and Networking Conference. Piscataway, NJ, USA: IEEE, 2014: 434-439.

[4] PHAM S, HAR D, KONG H. Smart power allocation for secrecy transmission in reciprocally cooperative spectrum sharing [J]. IEEE Transactions on Vehicular Technology, 2015, 58(5): 1875-1888.

[5] ZHANG N, LU N, CHENG N, et al. Cooperative spectrum access towards secure information transfer for CRNS [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(11): 2453-2464.

[6] HYOUNGSUK J, STEVEN W M, IL-MIN K, et al. Secure communications with untrusted secondary nodes in cognitive radio networks [J]. IEEE Transactions on Wireless Communications, 2014, 13(4): 1790-1805.

[7] KARIM K, EYLEM E. Secrecy in cognitive radio networks: turning foes to allies [C]∥IEEE International Symposium on Modeling & Optimization in Mobile, Ad Hoc & Wireless Networks. Piscataway, NJ, USA: IEEE, 2013: 194-200.

[8] OSBORNE M J, RUBENSTEIN A. A course in game theory [M]. Cambridge, MA, USA: MIT Press, 1994: 18-30.

[9] 宋婧, 丛犁, 葛建华, 等. 双层网络中一种协作博弈的动态资源分配方法 [J]. 西安交通大学学报, 2012, 46(10): 89-94. SONG Jing, CONG Li, GE Jianhua, et al. A dynamic resource allocation approach using cooperative game theory for two-tie networks [J]. Journal of Xi’an Jiaotong University, 2012, 46(10): 89-94.

[10]XIAO L, CHEN T H, LIU J L, et al. Anti-jamming transmission Stackelberg game with observation errors [J]. IEEE Communications Letters, 2015, 99(4): 1790-1805.

[11]ZHANG R, CUI S, LIANG Y C. On ergodic sum capacity of fading cognitive multiple-access and broadcast channels [J]. IEEE Transactions on Wireless Communications, 2010, 9(6): 2066-2075.

[12]GABRY F, ZAPPONE A, THOBABEN R, et al. Energy efficiency analysis of cooperative jamming in cognitive radio networks with secrecy constraints [J]. IEEE Wireless Communications Letters, 2015, 4(4): 437-440.

[13]STEPHEN B, LIEVEN V. Convex optimization [M]. Cambridge, UK: Cambridge University Press, 2004: 95-103.

[14]CHEN H, LI Y, JIANG Y, et al. Distributed power splitting for swipt in relay interference channels using game theory [J]. IEEE Transactions on Wireless Communications, 2015, 14 (1): 410-420.

附录A

定理1的证明可采用如下定理[13]进行证明。

定理4 当且仅当下述条件至少一个满足时,连续函数f是拟凹函数:①函数f是非减的;②函数f是非增的;③存在一点c∈domf,对于t≤c且t∈domf,函数f非减;对于t≥c且t∈domf,函数f非增。

具体证明过程和文献[14]中定理1的证明类似,这里不再详细叙述。

证毕。

附录B

证毕。

附录C

证毕。

[本刊相关文献链接]

陈鹏,邱乐德,王宇.卫星认知无线电检测门限与功率分配联合优化算法.2013,47(6):31-36.[doi:10.7652/xjtuxb201306 006]

李晓艳,张海林,郭超平,等.一种异步的认知无线电网络跳频算法.2012,46(12):30-35.[doi:10.7652/xjtuxb201212 006]

张正浩,裴昌幸,陈南,等.宽带认知无线电网络分布式协作压缩频谱感知算法.2011,45(4):67-71.[doi:10.7652/xjtuxb201104012]

王天荆,姜华,刘国庆.采用分组数据的序贯频谱感知方法.2015,49(12):34-39.[doi:10.7652/xjtuxb201512006]

王兵,白智全,董培浩,等.采用空时分组编码的动态分组加权合作频谱感知方案.2014,48(8):23-28.[doi:10.7652/xjtuxb201408005]

高锐,李赞,司江勃,等.一种双重序贯检测的协作频谱感知方法.2014,48(4):102-108.[doi:10.7652/xjtuxb201404018]

董恩清,刘伟,宋洋.采用三角形节点块处理无线传感器网络节点定位中节点翻转歧义的迭代方法.2015,49(4):84-90.[doi:10.7652/xjtuxb201504014]

钟艺玲,穆鹏程.单发多收无线窃听信道中的自适应保密速率传输方案.2015,49(4):104-109.[doi:10./xjtuxb201504 017]

魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法.2014,48(6):1-6.[doi:10.7652/xjtuxb 201406001]

蔡文炳,付红双,张水莲,等.一种无线信道密钥容量求解方法.2014,48(6):31-36.[doi:10.7652/xjtuxb201406006]

李建东,姜建,刘鑫一.采用时延限制和资源预测的异构无线网络选择策略.2014,48(2):74-79.[doi:10.7652/xjtuxb 201402013]

崔华力,钱德沛,张兴军,等.用于无线多跳网络视频流传输的优先级机会网络编码.2013,47(12):13-18.[doi:10.7652/xjtuxb201312003]

汪志伟,曹建福,郑辑光.一种面向分簇无线传感器网络的多信道跨层协议.2013,47(6):61-67.[doi:10.7652/xjtuxb 201306011]

高昂,李增智,赵季中.用于无线自组织网络的属性加密算法.2012,46(8):33-36.[doi:10.7652/xjtuxb201208006]

李彬,王文杰,殷勤业,等.无线传感器网络节点协作的节能路由传输.2012,46(6):1-6.[doi:10.7652/xjtuxb201206001]

(编辑 刘杨)

Cooperation Schemes Between the Primary Transmitter and Untrusted Secondary Transmitters in Cognitive Radio Networks Using Game Theory

MA Yayan,WANG Baoyun

(College of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications, Nanjing 210003, China)

Two cooperation schemes using game theory are proposed to solve the problem that the untrusted secondary transmitters(STs) will eavesdrop on the primary link in cognitive radio networks and to covert the hostile relation between the primary transmitter(PT) and STs into a cooperative one, and they are a Stackelberg scheme and an improved two-layer game.The STs work in half-duplex and prefer to transmit than to eavesdrop in the Stackelberg scheme. Hence, the PT plays the Stackelberg game with each ST, and then selects the ST who creates more interference to the unselected STs(i.e. the potential eavesdroppers) to transmit simultaneously. The Stackelberg scheme is then extended into a two-layer game to facilitate the competition among the STs. The outer framework is still a Stackelberg model and the PT plays game with all the STs as an entity, while the inner has an auction framework in which each ST improves its security rate as much as possible for the access opportunity. The PT will conduct cooperation with the ST having the highest security rate, so that more profit can be obtained. Numerical results show that application of these two proposed schemes results in a significant improvement: the security rate of the two schemes increases by 63% and 68% respectively, and the access opportunity of STs is 56% and 71% respectively.

security; game theory; cooperation; cognitive radio networks

2015-05-25。

马亚燕(1979—),女,博士生;王保云(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61271232,61372126);江苏省高校研究生科研创新计划资助项目(CXZZ12_0472)。

时间:2015-12-02

10.7652/xjtuxb201602011

TN409

A

0253-987X(2016)02-0061-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151202.1858.004.html