旋转机械振动信号的小波域维纳滤波去噪
2016-12-21杨尚君石现峰
杨尚君,张 峰,石现峰
(西安工业大学 电子信息工程学院,西安 710021)
旋转机械振动信号的小波域维纳滤波去噪
杨尚君,张 峰,石现峰
(西安工业大学 电子信息工程学院,西安 710021)
为了去除旋转机械振动信号采集传输过程中混入的噪声干扰,文中基于维纳滤波和小波阈值滤波,通过建立旋转机械振动信号采集模型,结合振动信号滤波要求,提出了旋转机械振动信号的小波域维纳滤波算法.利用工业现场旋转机械实测振动信号,对该算法进行仿真.结果表明:该算法保持了旋转机械振动信号的线性相位特性,滤波后信号未产生明显的幅度失真;小波域维纳滤波的均方误差小于维纳滤波和小波阈值滤波,去噪效果优于维纳滤波和小波阈值滤波.
旋转机械;振动;小波域维纳滤波;线性相位
旋转机械故障检测采用数字信号处理的方法对实际测量的振动信号进行分析,用以参数检测和质量评价.在采集及传输的过程中,振动信号不可避免的混入噪声干扰,对振动信号的滤波处理既要取得较好的效果,也要保证振动信号的均衡相位,以便根据这些特性,来进行状态检测和故障诊断,应用于旋转机械振动信号的滤波处理当中.
传统的有限冲击响应(Finite Impulse Response,FIR)滤波器和无限冲击响应(Infinite Impulse Response,IIR)滤波器,两者的滤波算法滤波效果和线性相位之间难以达到均衡[1];文献[2]采用维纳滤波对非平稳振动信号进行处理,研究表明未达到预期效果;文献[3]采用循环维纳滤波对振动信号进行周期性的分段处理,每段采用维纳滤波方法,有效的去除了自适应噪声,但是循环维纳滤波算法复杂度大;文献[4]基于离散余弦变换(Discrete Cosine Transform,DCT)算法,保留了信号的部分离散余弦变换域的点数,实现了数据的压缩,但是DCT滤波算法对于大数据的压缩存在着数据丢失,滤波效果差的问题.针对振动信号滤波的敏感相位和滤波效果的问题,文中将维纳滤波和小波阈值滤波相结合,通过建立旋转机械振动信号采集模型,结合振动信号滤波要求,提出旋转机械振动信号的小波域维纳滤波算法.利用工业现场旋转机械实测振动信号,对该算法进行仿真,以期满足滤波要求和线性相位,以适用于其他一维含噪信号的处理.
1 振动信号采集
旋转机械振动信号的采集模型如图1所示.图1中ω为旋转机械转轴转动的角频率, v为转轴转动的线速度,理想情况下振动信号可表示为
y=A+Bcos(ωt+φ)
(1)
式中:y为理想振动信号;A为振动信号的直流分量;B为振动信号交流分量的最大值;ω为旋转机械转轴转动的角频率;φ为振动信号的初始相位;t为振动信号的时长.

图1 传感器测量轴振动信号的采集模型
Fig.1 Collect model of the output signal
of the transducer measuring shaft
信号处理前将其直流分量去除,随机变量φ服从在[0,2π]区间的均匀分布,根据平稳随机过程的定义,有
E(y)=E[Bcos(ωt+φ)]=
(2)
Ry(t1,t2)=E[y(t1)y(t2)]=
(3)
式中:E(·)为数学期望;Ry(·,·)为自相关函数;t1,t2为不同时刻的信号时长.自相关函数仅与时间间隔(t2-t1)有关,理想状况下振动信号为平稳信号.由于现场采集过程中,振动信号不可避免会受到环境和设备自身噪声的干扰,噪声是非平稳的,故含噪的振动信号是非平稳振动信号.
根据工业现场的实际情况,对旋转机械实际振动信号进行实际采集.数据采集的相关参数如下:32倍频采样,采样频率为1 600 Hz,每通道连续采集128点.较为理想情况下,振动信号的时域波形如图2所示.
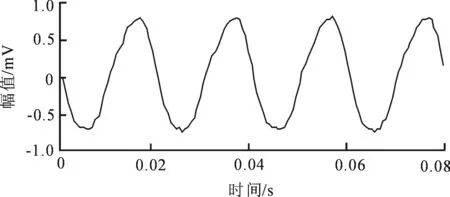
图2 理想情况振动信号时域波形
Fig.2 Time domain waveform of vibration signal in ideal condition
为研究去噪性能,对信号加入非平稳随机噪声,噪声点数为达到与采样点数匹配,故取128点,加噪后的振动信号如图3所示.
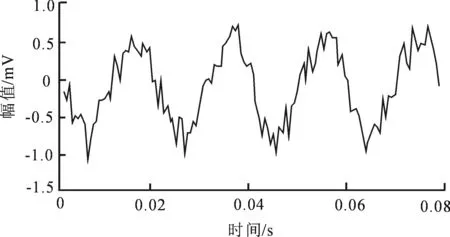
图3 加噪处理后的振动信号时域波形
Fig.3 Time domain waveform of vibration signal after adding noise
2 振动信号小波域维纳滤波算法
理想状况下,振动信号各次谐波的谱峰位置应出现在50 Hz的整倍频处,谱峰位置包含了转轴运行状态的有用信息,因此谱峰的准确性直接影响了后期的故障诊断.而初始相位的偏移会导致振动信号后期谱估计中谱峰的分裂或偏移,因此对于振动信号的滤波,单位冲击响应应具有较高的线性相位[5].振动信号频谱图的方差和分辨力性能也直接受到噪声的影响,因此为了获得较好性能的方差和分辨力,应尽可能的对振动信号的噪声进行去除.经典的FIR滤波器和IIR滤波器在滤波效果和线性相位方面均难以满足要求,故需要引入现代的维纳滤波算法来进行处理.根据最小均方误差准则[6],提出一种针对平稳过程的最优估计器.
2.1 振动信号的维纳滤波算法
假定观测信号模型为
x(n)=s(n)+w(n)
(4)
式中:s(n)为真实信号;w(n)为加性高斯白噪声,其分布为w(n)~N(0,δ2).根据FIR滤波器准则,有

(5)
式中: h(k)为FIR滤波器的单位取样响应;N为滤波器阶次;y(n)为滤波后信号.
维纳滤波算法原理如图4所示.其中Z-1表示Z变换,e(n)表示真实信号与滤波后信号的误差.

图4 Wiener滤波算法原理图
Fig.4 Wiener filtering schematic
均方误差为
(6)
若使均方误差最小,应满足维纳霍夫方程

(7)
式中:φxx(m)为观测信号x(n)的自相关函数;φsx(m)为真实信号s(n)与观测信号x(n)的互相关函数;m为遍历系数.维纳滤波算法适用于平稳随机信号[7],旋转机械振动信号在传输过程中不可避免的受到非平稳噪声的影响,因此,维纳滤波算法对旋转机械振动信号去噪具有局限性.阶次为64的维纳滤波实验结果如图5所示.

图5 维纳64阶次滤波振动信号时域波形
Fig.5 Time domain waveform of vibration signal for 64 order Wiener filtering
通过图5可以看出,振动信号的维纳滤波算法保持了信号的初始相位均衡,但滤波效果较差,达不到后期信号处理的要求.
2.2 振动信号小波阈值滤波及小波变换
根据小波阈值滤波,对含噪声信号进行正交小波变换.选择合适的小波基函数和分解小波层数,对含噪信号进行正交小波分解,得到对应的小波分解系数,其中包含了低频系数和高频系数.选择合适的阈值,对分解后的系数进行阈值处理.每一层小波系数再进行量化处理.进行小波反变换.将阈值处理后的小波系数进行重构,得到小波阈值滤波后的信号.实验选用软阈值函数进行处理[8],数学表达式为
δ(σ)=sgn(σ)(|σ|-λ),|ω|>λ
(8)
式中:σ为小波系数;λ为阈值;δ(σ)为被估计信号小波系数的估计值.实验选取最小极大方差阈值,则所选的阈值为
(9)
根据选用的Coif5小波基,分解2层,小波阈值滤波的结果如图6所示.
从图6中可以看出,直接进行小波阈值去噪处理的信号取得了较好的平滑特性,但滤波后信号产生了失真,不能作为后期的信号处理对象.
利用Haar小波作为小波基将信号从时域转化为小波域[9].Haar小波基函数为

(10)

图6 小波阈值滤波振动信号时域波形
Fig.6 Time domain waveform of vibration signal for wavelet threshold filtering
对于非平稳过程,功率谱密度与频率的幂成反比的,振动信号在经小波变换后能够,不同尺度间较强的相关性可有效去除,可以认为非平稳信号在经过小波变换后起到了信号的白化作用[10],满足上述结果的条件须进行正交小波变换,Haar小波作为简单的正交函数,将振动信号从时域转化到小波域选用Haar小波,降低了信号的非平稳特性的同时,保留了信号的有用信息[11-12].
2.3 基于小波变换的维纳滤波算法
根据维纳滤波的原理,在构建维纳霍夫方程前需已知加噪信号和期望信号,利用小波阈值去噪对加噪振动信号进行简单的阈值去噪处理,将原始振动信号作为期望信号,两者同时变换到小波域进行维纳滤波处理[13].小波域维纳滤波算法过程如下:① 将加噪的振动信号进行小波阈值去噪进行预处理,得到信号,用于构建小波域的维纳霍夫方程;② 分别将原始振动信号(作为期望信号)和小波阈值去噪信号两者分别利用Haar小波进行小波变换,分别提取两者的近似分量和细节分量;③ 利用两者细节分量构建维纳霍夫方程,对小波阈值去噪信号的细节分量进行滤波处理,利用两者近似分量构建维纳霍夫方程,对小波阈值去噪信号的近似分量进行滤波处理;④ 利用小波反变换函数对上述信号处理结果进行反变换,其利用的小波基仍为Haar小波.
3 仿真及分析
小波域32阶次维纳滤波算法信号处理结果如图7所示.通过图7和图5的对比,小波域维纳滤波算法具有较好的线性相位特性,振动信号初始相位没有发生明显偏移.在小波域维纳滤波的滤波阶数小于维纳滤波阶数的同时,小波域维纳滤波能取得更好的滤波效果.根据图7和图6的比较,利用小波阈值滤波算法保证了振动信号滤波后的平滑特性,该算法可用于实际的振动信号去噪环境中.由于计算量较大,该算法可做振动信号的离线分析处理.
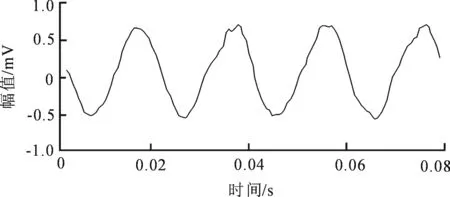
图7 小波域维纳滤波振动信号时域波形
Fig.7 Time domain waveform of vibration signal for Wiener filtering in wavelet domain
分别计算各种算法滤波后的结果与原始振动信号做均方误差的求解,进行算法性能定量分析和对比,得出数据见表1.
表1 算法性能定量分析
Tab.1 Quantitative analysis of algorithm performance

滤波算法均方误差维纳滤波0.0097小波阈值滤波0.0075小波域维纳滤波0.0032
从表1可看出,小波域维纳滤波的均方误差要小于维纳滤波和小波阈值滤波,小波域维纳滤波算法性能优于各种单独算法,小波域维纳滤波算法滤波后的信号更接近原始的振动信号.
利用小波域维纳滤波算法对振动信号进行去噪处理,对其结果进行频谱分析,采取周期图法,功率谱密度(Power Spectral Density,PSD)估计图如图8所示.f为频率,DPS为功率谱密度.

图8 滤波后振动信号的频谱图
Fig.8 Power spectrum of vibration signal after filtering
根据振动信号的采集模型,信号每周期采样32点,采样频率为1 600 Hz,因此信号的固有频率为50 Hz.从图8中可以看出,滤波后振动信号的谱峰处于50 Hz整倍频处,功率谱图中的谱峰具有较好的尖锐程度,分辨率性能较好,具有较强辨别信号的能力,且谱峰没有发生偏移或分裂的现象.因此滤波后的振动信号适用于后期的旋转机械故障检测.
4 结 论
1) 将振动信号从时域转化到小波域,降低了振动信号的非平稳特性,小波域维纳滤波算法保留了维纳滤波算法的线性相位特性,信号原有的初始相位未发生偏移,滤波后的信号幅值和相位未产生失真.
2) 小波域维纳滤波去噪性能优于维纳滤波和小波阈值滤波,均方误差小于维纳滤波和小波阈值滤波.
3) 小波域维纳滤波后的振动信号,功率谱图中的谱峰处于50 Hz整倍频处,分辨率性能好,辨别信号的能力优于维纳滤波,谱峰没有发生偏移或分裂,适用于后期的旋转机械故障检测.
[1] 张峰,石现峰,张学智.数字信号处理原理及应用[M].北京:电子工业出版社,2012.
ZHANG Feng,SHI Xianfeng,ZHANG Xuezhi.Principle and Application of Digital Signal Processing[M].Beijing:Electronics Industry Press,2012.
(in Chinese)
[2] 明阳.基于循环平稳和盲源分离的滚动轴承故障特征提取方法研究[D].上海:上海交通大学,2013.
MING Yang.Study on Cyclostationarity and Blind Source Separation-Based Rolling Element Bearing Fault Feature Extraction[D].Shanghai:Shanghai Jiao Tong University,2013.(in Chinese)
[3] 明阳,陈进,董广明.基于循环维纳滤波器和包络谱的轴承故障诊断[J].振动工程学报,2010,23(5):537.
MING Yang,CHEN Jin,DONG Guangming.Rolling Bearing Fault Diagnosis Based on Cyclic Wiener Filtering and Envelop Spectrum[J].Journal of Vibration Engineering,2010,23(5):537.(in Chinese)
[4] 管博,胡劲松.基于DCT的旋转机械振动信号无相移滤波方法研究[J].汽轮机技术,2007,49(4):285.
GUAN Bo,HU Jinsong.Research on the Method of the Vibration Signal of Rotating Machinery Based on DCT[J].Turbine Technology,2007,49(4):285.
(in Chinese)
[5] RINALDO R,VISETTI A.Relations Between the K -Dimensional Unconstrained and Linear Phase FIR Wiener Filters[J].Multidimensional Systems and Signal Processing,1995,6(4):347.
[6] 李楠.一种小波变换与维纳滤波结合的语音抗噪研究[J].电声技术,2007,31(5):46.
LI Nan.Study on the Speech Antinoise Based on Wavelet Transform and Wiener Filtering[J].Electro Acoustic Technology,2007,31(5):46.(in Chinese)
[7] XU P,MIAO Q,TANG X.A Denoising Algorithm via Wiener Filtering in the Shearlet Domain[J].Multimedia Tools and Applications,2014,71(3):1529.
[8] 杨玲香,姚斌.基于Canny算子的小波域维纳滤波去噪方法[J].兵团教育学院学报,2009,19(5):35.
YANG Lingxiang,YAO Bin.Denoisng Method via Local Wiener Filtering in Wavelet Domain Based on Canny Operator[J].Journal of Bingtuan Education Institute,2009,19(5):35.(in Chinese)
[9] ZHONG K,LEI X,LI S.Wiener Filter Based Channel Estimation for High-Speed Communication Environments[J].Wireless Personal Communications,2013,69(4):1819.
[10] 李东兵,李国平,滕国伟,等.一种基于小波和Wiener相结合图像去噪新方法[J].电视技术,2013,37(13):26.
LI Dongbing,LI Guoping,TENG Guowei,et al.New Method of De-noising Based on Wavelet and Wiener Filtering[J].Video Engineering,2013,37(13):26.(in Chinese)
[11] RAO R,MURTHY R,VENKATA R.Speech Enhancement Using Cross-correlation Compensated Multi-band Wiener Filter Combined with Harmonic Regeneration[J].Journal of Signal and Information Processing,2011(2):117.
[12] 胡耀斌,陈艾华,张春良.小波分析与维纳滤波相结合的消噪方法研究[J].电力系统通信,2006,27(162):42.
HU Yaobin,CHEN Aihua,ZHANG Chunliang.Research of Denoising Technology about Wavelet Analysis with Wiener Filter[J].Communication of Power System,2006,27(162):42.(in Chinese)
[13] SINDELAR V,NIKOLAUS G.An Adaptation of the Wiener Filter Suitable for Analyzing Images of Isolated Single Particles[J].Journal of Structural Biology,2011,176(1):60.
(责任编辑、校对 张 超)
Wavelet Domain Denoising for Rotating Machinery Vibration Signal Based on Wiener Filtering
YANGShangjun,ZHANGFeng,SHIXianfeng
(School of Electronic Information Engineering,Xi’an Technological University,Xi’an 710021,China)
In order to remove the noise in rotating machinery vibration signal during the acquisition and transmission process, the algorithm of Wiener filtering in wavelet domain is proposed to meet the requirements of vibration signal filtering,based on Wiener filtering and wavelet threshold filtering,through the establishment of rotating machinery vibration signal acquisition model.Using the rotating machinery vibration signal which is actual measurement in the industrial field, the algorithm is simulated.The result shows: This algorithm can maintain the linear phase characteristics for rotating machinery vibration signal,the filtered signal doesn't produce the amplitude distortion; The mean square error of Wiener filtering in wavelet domain is less than that of Wiener filtering and wavelet threshold filtering.The denoising result is better than Wiener filtering and wavelet threshold filtering.
rotating machinery;vibration;Wiener filtering in wavelet domain;linear phase
10.16185/j.jxatu.edu.cn.2016.10.015
2016-01-06
国家自然科学基金项目(60972095;61271362);陕西省科技厅自然基金项目(2012JQ8008);陕西省教育厅科技专项(2012JK0545)
杨尚君(1991-),男,西安工业大学硕士研究生.
张 峰(1979-),男,西安工业大学副教授,主要研究方向为信号与信息处理、嵌入式技术应用、自动控制及数据库技术运用.E-mail:zf_zx963@163.com.
TN911.4
A
1673-9965(2016)10-0856-05
