几种改进的BP神经网络在GPS高程拟合中的应用比较

魏宗海

(河北省地矿局第三地质大队,张家口075000)



几种改进的BP神经网络在GPS高程拟合中的应用比较

魏宗海

(河北省地矿局第三地质大队,张家口075000)

为了提高GPS高程拟合的精度和效率,本文分别利用几种常见的算法对标准BP神经网络进行了改进,结合控制网测量实例,分别利用外符精度、内符精度、测试步长以及运行时间4个指标对拟合结果进行评价。结果表明,不同改进算法的设计分别能有效提高拟合的精度和效率,在实际的工程实践中,可以根据具体拟合要求采取合适的算法对BP神经网络进行改进。

BP神经网络;GPS高程拟合;高程异常；算法改进

0 引 言

目前,GPS技术以其定位精度高,测量速度快以及操作简单等优点正逐渐取代传统的测量技术[1]。GPS测量系统所采用的坐标系是WGS-84坐标系,在进行水准测量时获取的是大地高H1,而我国采用的是以似大地水准面为基准的正常高H2。因此,需要建立合适的模型实现两者之间的转换。在忽略垂线偏差的情况下,大地高与正常高之间的关系可近似表示为

ε=H1-H2,

(1)

式中,ε为高程异常。通过上式可以看出,实现两者转换的关键在于如何精确的获取高程异常值,但高程异常值无法直接通过测量仪器进行获取,目前也并没有统一的数学模型进行计算[2]。因此,如何获取高精度的高程异常值成为将GPS技术应用于我国水准测量建设的关键[3]。

目前,国内外学者已经建立并实现了多种求取高程异常值的模型和方法,主要有重力模型法、函数模型法、随机模型拟合法以及神经网络等。每种模型都有其各自的优缺点[4]。例如重力模型法,需要的参数过多,模型复杂程度高,适用性低,但得到的高程异常值精度较高。目前,BP神经网络技术以其在处理非线性问题所表现出来的优势,正逐渐成为求取高程异常值的主要技术方法。

本文针对BP神经网络技术在处理非线性映射问题上,表现出来的网络参数难确定,收敛速度较慢且易陷入极小值等问题,分别应用不同的算法进行改进,主要包括附加动量项、自适应学习速率、弹性BP、变梯度算法、牛顿法、L-BFGS以及LM算法。结合GPS控制网测量实例,分别利用外符精度、内符精度、测试步长以及运行时间四个指标对拟合结果进行评价。本文采用的训练集中输入向量共包含四个,分别为(X,Y,H1,H2),标准输出为已知的高程异常值,在进行仿真时输入向量仅为(X,Y,H1,H2),高程异常值未知。

1 基本BP神经网络算法

1.1 网络结构

误差反向传播多层前馈神经网络(BP神经网络),是目前在处理非线性映射问题中应用较为广泛的一类神经网络[5]。网络结构由三部分构成,分别为输入层,隐含层与输出层。相邻神经元之间实现全连接,而同层神经元互不连接[6]。输入层与输出层节点数目主要由输入输出向量的维数来确定。对于隐层节点数目的确定,目前并没有指定的标准进行参考,一般采用试错法进行选择。根据Kolmogorov定理可知,单隐层BP神经网络能在闭集上以任意精度逼近任意非线性连续函数,所以本文隐层数量设置为1[7]。其中网络结构如图1所示。

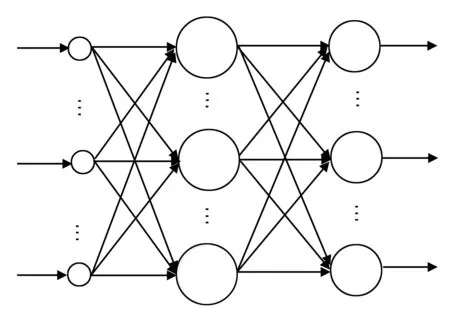
图1 BP神经网络的结构

1.2 BP神经网络学习算法步骤[8]

第一步:设置变量。

Xk=[xk1,xk2,…,xkM](k=1,2,…,N)为输入向量,或称训练样本,N为训练样本的个数。

Yn(n)= [yk1(n),yk2(n),…,ykp(n)]T

(k=1,2,…,N).

为第n次迭代时网络的实际输出。

dk=[dk1,dk2,…,dkp]T(k=1,2,…,N)为期望输出。

第二步:初始化,赋给各映射神经元一个较小的随机非零值,即初始权值。

第三步:对输入样本Xk前向计算BP神经网络每层神经元的输入信号u和输出信号v.

第四步:由期望输出dk和上一步求得的实际输出计算误差E(n),判断其是否满足要求,若满足转至第七步,不满足转至第五步。

第五步:判断n+1是否大于最大迭代次数,若大于转至第七步,若不大于则对输入样本Xk反向计算每层神经元的局部梯度δ.

第六步:按公式:

Δωij(n)=aΔωmj(n-1)+ηδj(t)νm(t),

(2)

计算权值修正量Δω,其中a为学习率,并修正权值n=n+1,转至第四步。

第七步:判断是否学完所有的训练样本,是则结束,否则进入第三步。

2 改进神经网络学习算法

2.1 附加动量法

在标准BP神经网络中,权值的调整一般主要考虑误差在梯度上的作用,此时,网络在误差修正过程中易陷入到极小值中。附加动量法的实质是在最后一次权值修正时,通过增加一个动量项来滑过可能出现的极小值点。同时在附加动量算法中,可以设置一个较大的学习率,而不会造成学习过程的发散,因为即使修正过量时,该算法总是可以使修正量减小,以保持修正方向向着收敛的方向进行。因此,附加动量算法的收敛速率较快,学习时间较短。

2.2 自适应学习速率

由BP神经网络的误差传递特点可知,其学习率在整个训练过程中一直是保持不变的,包括前面提到的附加动量法进行的改进,但训练程度的好坏与学习率的选择具有紧密的联系,同时学习算法也对学习率具有很强的敏感性。当学习率的选择较大时,训练过程中权值修正的程度较高,此时算法的不稳定性将会加强;当学习率的取值较小时,单位步长内误差修正的程度较低,容易加长训练的时间。

自适应学习速率算法对BP神经网络的修正主要集中在学习率上,调整后的BP神经网络在训练过程中,学习率是不断随着误差曲面以及运行步长而改变的,这主要是通过在误差调整过程中加入增量因子与缩量因子完成的。当误差随训练步长不断减小时,可适当增加步长,使学习率乘以增量因子;当误差随训练步长不断增加时,可适当减小步长,使学习率乘以缩减因子。下式给出一个自适应学习速率的调整公式,此时增量因子与缩量因子分别为1.05与0.7,

(3)

式中: η(k)与E(k)分别为第k步的误差平方与学习速率,初始学习速率的选取范围具有很大的随意性。

2.3 L-BFGS算法[9]

拟牛顿法(L-BFGS)算法是对牛顿法(BFGS)算法的进一步优化,在迭代过程中,通过保存部分梯度算子和模型修正量的信息来求取伪海森矩阵,以此来避免海森矩阵的直接存储与精确求解,从而使得解算的复杂度大大降低。针对极小化问题,精确的线搜索还可以提高L-BFGS算法收敛性,加速收敛,同时计算精度也有一定的提高。

2.4 LM算法[10]

Levenberg-Marquart 算法,习惯上简称为LM算法,该算法同时具备了牛顿法以及变梯度算法的相关优势。其中牛顿法方面主要表现在其在迭代过程中能在最优值附近产生一个理想搜索方向;在变梯度算法方面其同样在迭代开始进行时是沿着梯度最陡的方向进行的。但LM算法引入了Hesse阵,并且求取方法为完全结算,因此算法的复杂程度较高,在进行迭代的过程中需要的时间更长,但保证了结果的准确性。

2.5 其他改近算法[11]

其他常用的改近算法还有弹性BP、变梯度算法以及牛顿法等。其中弹性BP算法的基本原理是权重和阈值更新值的直接修改,通过引入Resi-

lient有弹性的概念实现对权值的修正;变梯度算法对BP神经网络的修正主要反映在误差的传播方向上,其误差函数是沿着梯度变化的方向进行修正的;牛顿法在算法形式上等同于所有流行的优化方法,即首先确定初始搜索方向,沿着此方向进行一维搜索,确定该方向的极小值点,确定后以该点为出发点,再此重新确定搜索方向,一直重复进行,直到函数梯度小于训练预设的梯度。

3 实验与结果比较

3.1 实验区域控制网

高程异常的变化值与地形起伏有很大关系,一般来讲平原区高程异常差距较小,而山地高程异常差距较大。目前在平原地区常用的是二次曲面拟合与神经网络模型;而在地形起伏较大的区域常用的则是重力模型法。本文主要研究各改进神经网络在平原地区拟合效果的比较,因此以某一区域面积约为10 km2的地势较平缓的地区为例,对该地区布设GPS控制网,网形中各控制点之间的距离约为1 km2,对网中控制点按照B级测量要求进行施测,并对部分控制点按照二等水准测量进行联测。测量成果如表1所示。

表1 B级GPS高程和二等水准测量成果

3.2 各改进算法拟合效果比较

本文将1～12号控制点定为训练点,13～19号控制点定为检验点。首先进行BP神经网络的训练,将各训练点的横坐标、纵坐标、GPS高程以及水准高程当做输入向量,并将其高程异常值当做标准输出。设定训练步长为2 000,目标误差定位0.000 01 m,激活函数为Sigmoid函数,在网络训练结束后进行仿真,再此将训练点与检验点的横纵坐标、GPS高程以及水准高程作为输入向量,仿真输出值与标准高程异常值之差即为拟合残差。基于上述步骤,分别利用上述各算法改进的BP神经网络进行拟合检验,结果如表2所示,对于拟合误差的精度用cm表示。

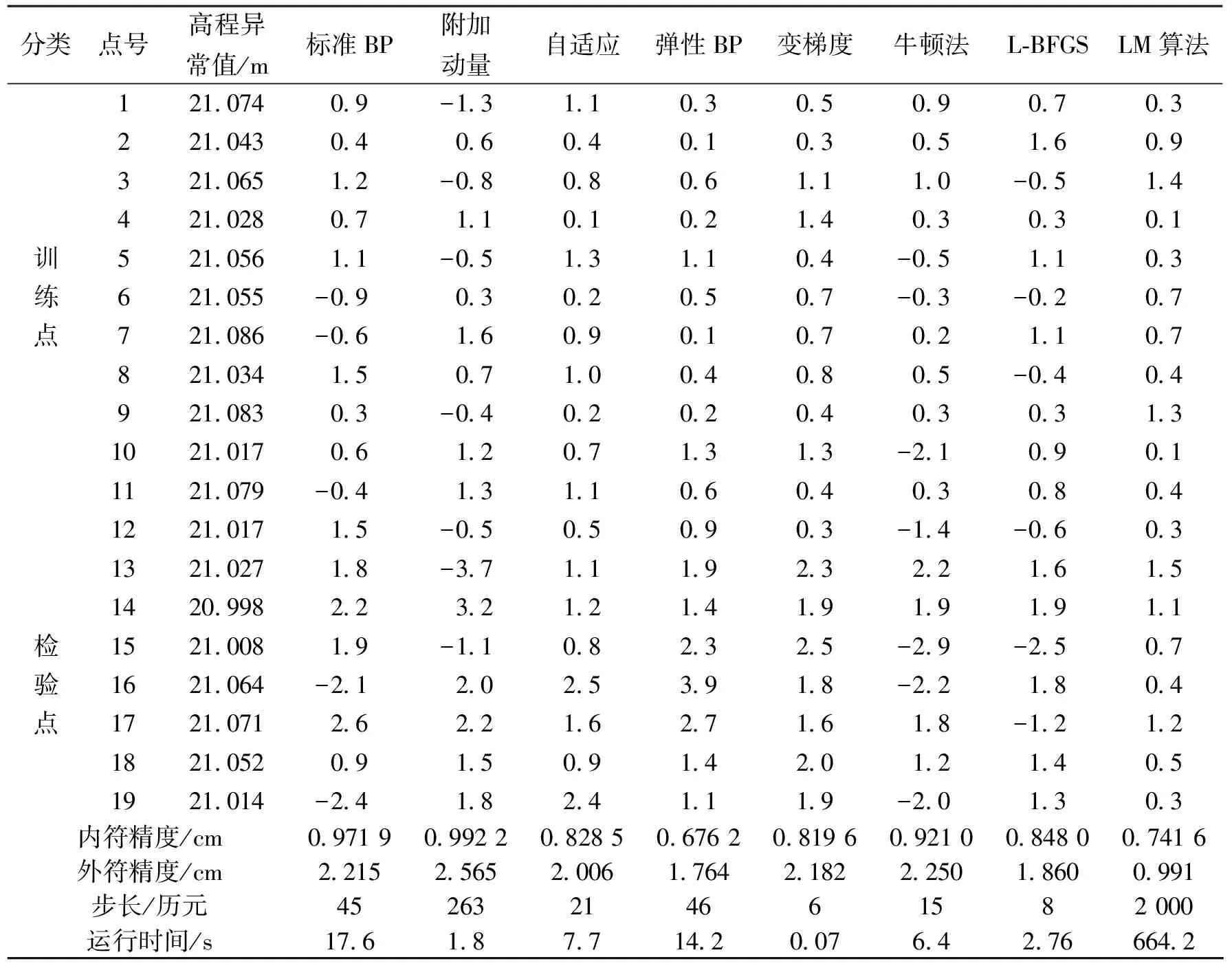
表2 不同改进算法拟合的控制点高程异常误差

根据表2及图2可知,将改进的BP神经网络学习算法应用于GPS高程拟合的方法是可行的,并且不同改进算法的设计分别能有效提高拟合的精度和效率。例如,附加动量项可以避免网络陷入局部极小值点;变梯度算法和牛顿法可以加快收敛速度。各改进算法在内符精度方面差距并不大,但对于验证性控制点而言,外符精度差距较大。在运

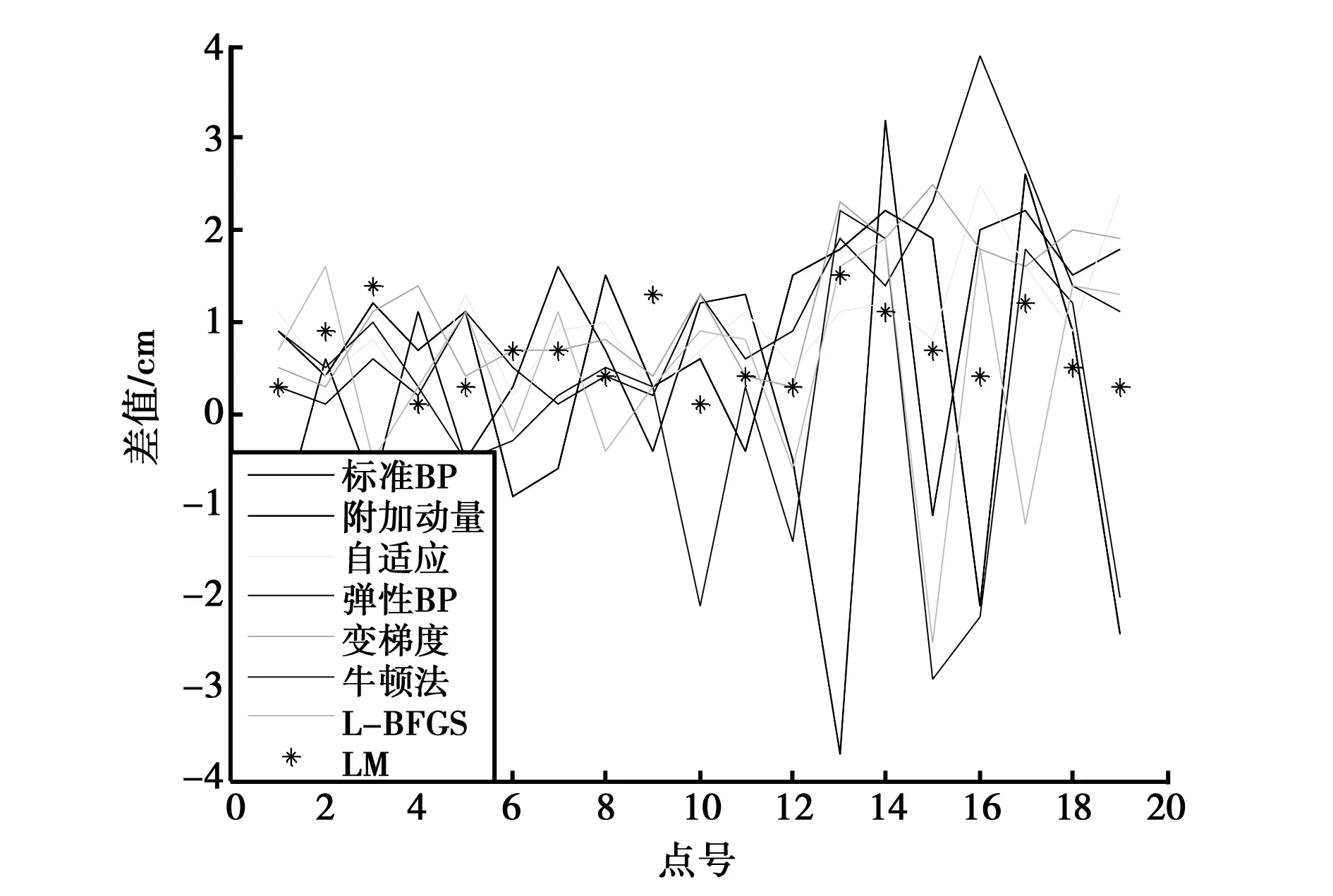
图2 不同改进算法得到的高程异常误差分布图

行时间方面,由于各算法采用的训练方法不同,训练结果也有很大的差距。对于拟合精度而言,最高的是LM算法;对于拟合效率而言,最高的是变梯度算法。

4 结束语

经过试验和结果分析,可以得出如下几个结论:

1) 在测量精度方面,基于LM算法改进的BP神经网络技术的拟合精度最高,但LM算法要对Hesse阵进行近似计算,所以算法的复杂度较高,迭代时间较长。

2) 在拟合效率上,变梯度算法改进的BP神经网络由于误差函数是沿着变化的方向进行搜索,所以收敛的速度更快。但变梯度算法仅对误差传播方向进行修正,并未对误差传播机制进行变革,使得拟合的精度较标准BP神经网络而言,并未有所改善。

3) 在实际的GPS高程拟合中,应用BP神经网络得到的高程异常是可以直接满足水准测量需求的。本文通过实验证明了不同改进算法的设计分别能有效提高拟合的精度和效率。其中,在对拟合精度要求较高时,可以采用弹性BP或LM算法进行改进;在对拟合效率要求较高时,可以采用附加动量项、变梯度、牛顿法以及自适应算法进行网络改进;在对两者要求均较高时,可以采用L-BFGS算法进行改进。

[1] 孙传胜,杨国东,吴琼.神经网络在 GPS高程拟合中的应用[J].测绘通报,2011(8):48-50.

[2] 王树海.转换GPS高程的BP神经网络方法研究[J].测绘科学,2008,33(6):78-80.

[3] 赵辉,张书毕,张秋昭.基于加权总体最小二乘法的GPS高程拟合[J].大地测量与地球动力学,2011(5):88-91.

[4] KAVOGLU T, SAKA M H. Modeling local GPS/leveing geoid undulations using artificial neuralnetwork[J].Journalof Geodesy,2004,78(9):520-527.

[5] 朱卫东,李全海.基于标准化动量神经网络的GPS高程转换[J].大地测量与地球动力学,2010,3(1):123-125.

[6] 卢献健,晏红波,梁月吉,等.各组合模型在GPS 高程拟合中的应用[J].研究测绘通报,2015(5):20-23.

[7] 和会,闻洪峰,魏太渊.基于 LM—BP神经网络的GPS高程拟合算法研究[J].测绘与空间地理信息,2011,34(6):95-97.

[8] 张磊.基于人工神经网络的GPS高程异常拟合方法的研究与实现[D].长安:长安大学,2012.

[9] 何美琳,文鸿雁,潘元进,等.GPS高程拟合的方法比较[J].测绘科学,2013,38(3):63-65.

[10] 张自敏,樊艳英,陈冠萍.LM-BP神经网络在农业总产值预测的应用[J].安徽农业科学,2014,42(28):109-111.

[11] 秦宁,基于整体最小二乘面拟合及其在GPS高程拟合中的应用研究[D].成都:西南交通大学,2015.

Comparison of Several Improved BP Neural Network in GPS Height Fitting

WEI Zonghai

(HebeiProvincialBureauofGeologyThirdGeologicalBrigade,Zhangjiakou075000,China)

In order to improve the efficiency and accuracy of GPS height fitting. In this paper, the use of several common algorithms of standard BP neural network was improved, combined with the control network measurement examples, respectively using the match precision and match accuracy, the testing step size and running time four indicators, evaluates the results of fitting.The results show that the improved algorithm design can effectively improve the fitting precision and efficiency, in the actual engineering practice, the project can according to the specific fitting to take appropriate algorithm to improve the BP neural network.

BP neural network; GPS heightfitting; height anomaly; algorithm improvement

10.13442/j.gnss.1008-9268.2016.05.020

2016-06-01

P228.4

A

1008-9268(2016)05-0099-05

魏宗海 (1982-),男, 高级工程师, 主要从事测绘新技术的开发与利用。

联系人： 魏宗海 E-mail: 15726207432@163.com