同时考虑公共点新老坐标误差的三维坐标转换模型

王阿昊,王解先,陈俊平

(1.同济大学 测绘与地理信息学院,上海 200092;2.中国科学院上海天文台,上海 200030;3.上海市空间导航与定位技术重点实验室,中国科学院上海天文台,上海 200030)



同时考虑公共点新老坐标误差的三维坐标转换模型

王阿昊1,2,王解先1,陈俊平2,3

(1.同济大学 测绘与地理信息学院,上海 200092;2.中国科学院上海天文台,上海 200030;3.上海市空间导航与定位技术重点实验室,中国科学院上海天文台,上海 200030)

传统意义上求解三维坐标转换的7个参数是基于间接平差模型,仅考虑新坐标系下公共点的误差。本文在此基础上,同时考虑老坐标系的公共点误差,采用附有参数的条件平差模型进行解算,通过实例计算,两种平差模型所求转换参数一致。精度分析时,绘制坐标转换残差的频率分布直方图,新模型的转换残差分布的更集中,其分布区域明显小于间接平差模型;当公共点个数在3个以上时,新模型的验后单位权中误差σ0始终小于间接平差模型,其σ0值约为间接平差模型的1/3到2/3.

坐标转换;七参数;间接平差;附有参数的条件平差;残差;验后单位权中误差

0 引 言

空间直角坐标转换广泛应用于大地测量、摄影测量、GPS测量及工业测量等领域,在大地测量中,有WGS-84世界大地坐标系、1954北京坐标系、1980西安坐标系及CGCS2000坐标系的相互转换;在摄影测量领域,建立共线方程及空间后方交会均以空间直角坐标转换为基础;随着GPS及INS技术的发展,对飞机、汽车等移动载体的姿态测量成为热门,任意角度的空间坐标转换十分重要[1];工业测量中,大型设备的测量空间大,精度要求高,测量环境不佳,现一般采用多站位联合测量,需将各站测量数据转换到同一坐标系下[2]。

目前,三维坐标转换常采用七参数法,通过三个以上的公共点,按间接平差模型建立误差方程,利用泰勒级数展开将模型线性化,然后解算3个旋转参数、3个平移参数和1个尺度因子,该法将老坐标系下公共点坐标视为无误差的值,仅考虑新坐标系下公共点的误差,而实际情况并非如此。本文将同时考虑两套坐标系下公共点的误差,采用附有参数的条件平差模型进行解算,以残差V和验后单位权中误差σ0作为精度指标,对两种方法进行比较。

1 模型表示与精度指标

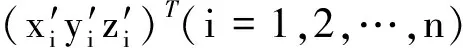
两个坐标系下公共点的转换关系为[3]

(1)

式中: (x0,y0,z0)为平移参数; (α,β,γ)为旋转参数; λ为尺度因子; R1(α)是把老坐标绕X轴旋转α角得到的旋转矩阵; R2(β)是把老坐标绕Y轴旋转β角得到的旋转矩阵; R3(γ)是把老坐标绕Z轴旋转γ角得到的旋转矩阵。该模型适合任意旋转角的三维坐标转换

(2)

(3)

(4)

1.1 间接平差转换模型

按间接平差模型,对每个公共点列出误差方程[3]

(5)

式中:vi=(vxivyivzi)T为新坐标系下公共点的转换残差。

(6)

式中,偏导数和常数项为

(7)

(8)

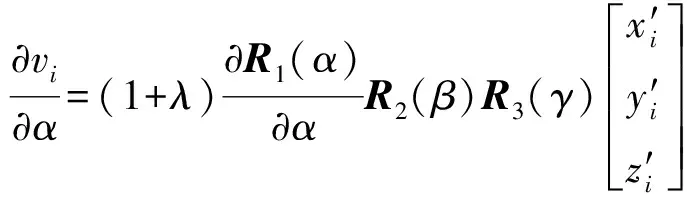
(9)

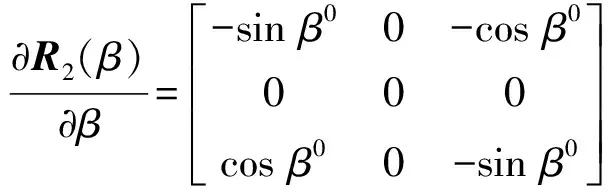
(10)

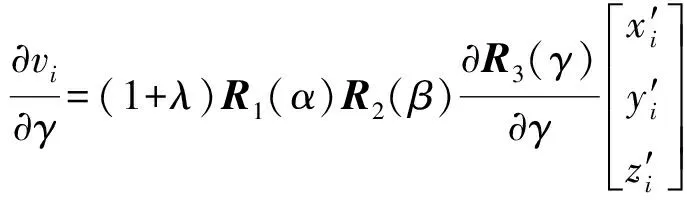
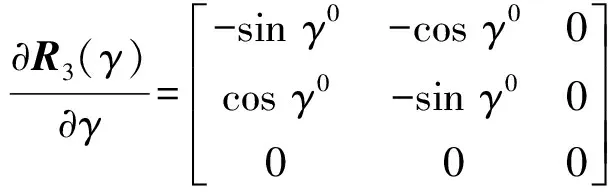
(11)

(12)

由误差方程式(6)组成法方程X=(BTPB)-1

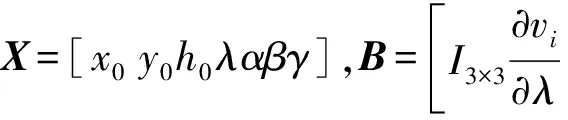
1.2 附有参数的条件平差转换模型

同时考虑新老两套坐标系下公共点的误差,函数模型为

(13)

将式(13)按泰勒级数展开,并对所求的7个参数取近似值,利用附有参数的条件平差模型,列出形如AV+CX-W=0的改正数条件方程[4]:

(14)

(15)

1.3 精度指标

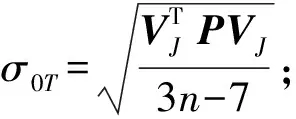
2 算例

为了比较两种三维坐标转换模型的精度,本文采用实测的29个GPS公共点坐标,按间接平差模型和附有参数的条件平差模型,分别计算从北京54坐标系转换到WGS-84坐标系的7个转换参数,两种计算结果一致,如表1所示。

在两种模型下,分别计算这29个GPS公共点的坐标转换残差,结果如表2所示。

表1 转换参数

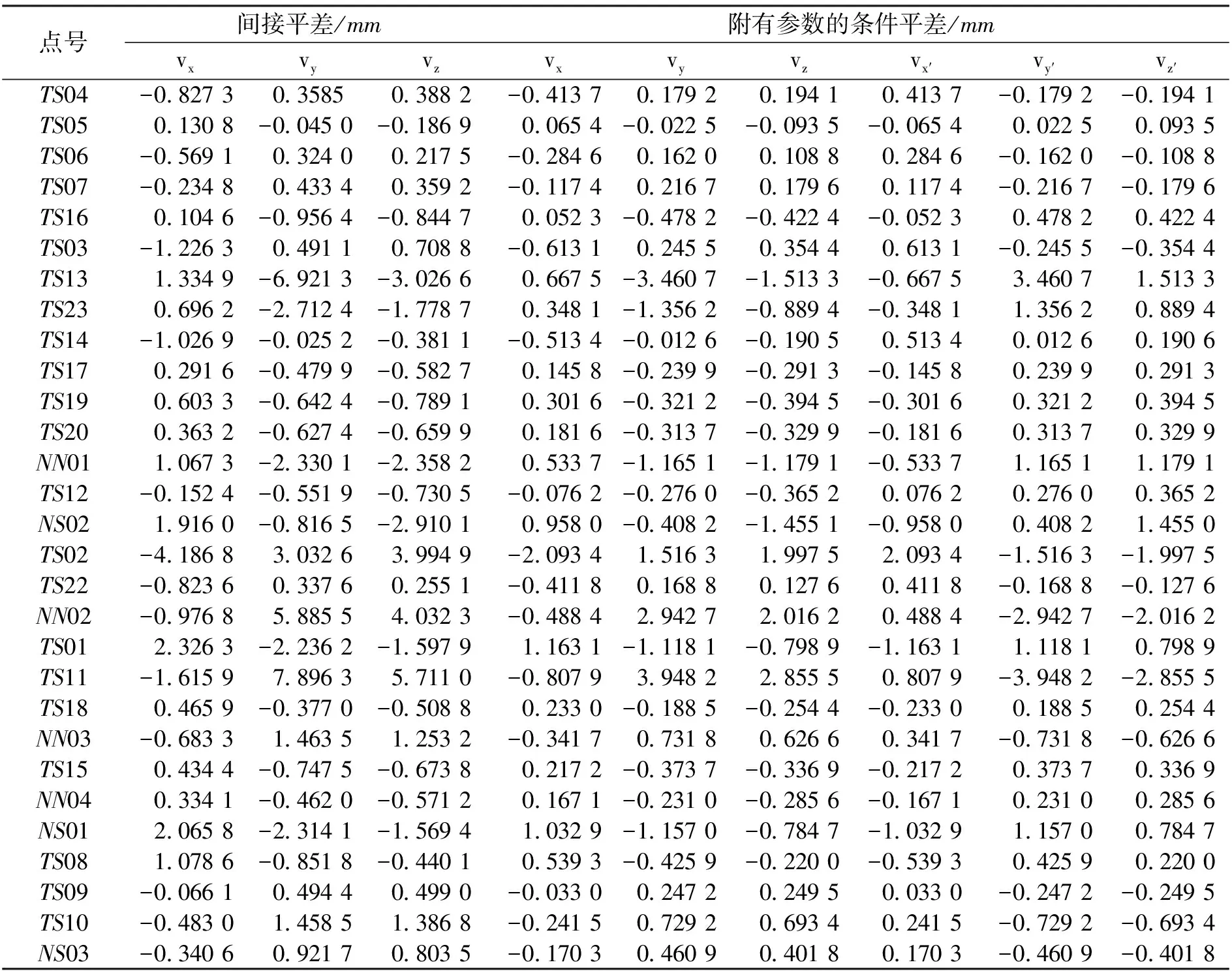
表2 坐标转换残差

根据表2结果,绘制两种模型在新坐标系(WGS-84坐标系)下各个方向上坐标转换残差的频率分布直方图,如图1所示,该坐标转换残差即为表2中的vx,vy,vz,在统计时各个方向均有29个残差值进行对比。

图1 坐标转换残差的频率分布直方图

由图1可知,采用附有参数的条件平差模型进行解算,其X方向的坐标转换残差在[-3,2]mm,Y和Z方向的转换残差分别在[-4,4]mm和[-2,3]mm,与间接平差模型相比,三个方向的转换残差分布更集中,且残差值越小的区域里,残差个数分布越多。

为了更全面的分析模型精度,并验证模型的稳定性,现依次选取前5个、10个、15个、20个、25个和全部29个GPS公共点,分别计算其验后单位权中误差σ0,统计结果如表3所示。

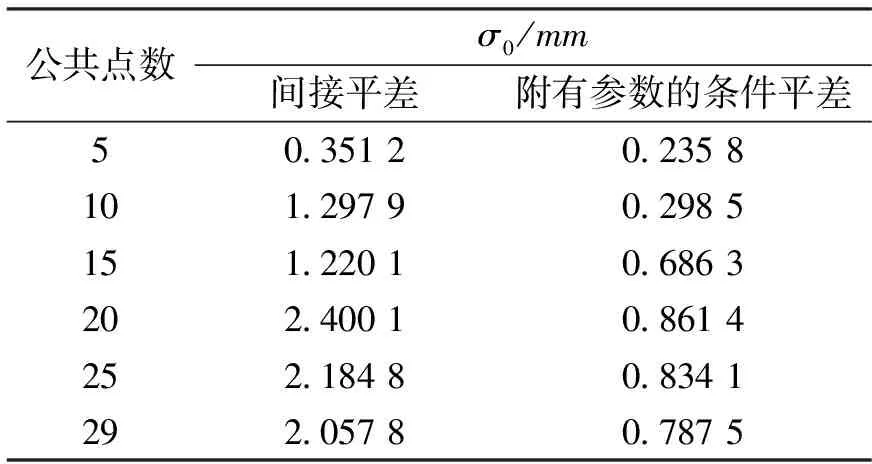
表3 验后单位权中误差

从表3可知,采用附有参数的条件平差模型进行三维坐标转换,其验后单位权中误差明显小于间接平差模型。公共点数在10个以上时,间接平差模型的σ0最小值为1.22,而附有参数的条件平差模型的σ0最大值仅为0.861 4,其减小幅度明显。

3 结束语

本文同时考虑新老两套坐标系下公共点的误差,建立附有参数的条件平差模型对三维坐标转换中涉及的7个参数进行解算,该模型适合任意旋转角的三维坐标转换。精度分析时,以坐标转换残差V和验后单位权中误差σ0做精度指标,与间接平差模型的计算结果进行比较,通过算例可得如下结论:

1) 采用附有参数的条件平差模型,其X、Y、Z方向上的坐标转换残差明显小于间接平差模型,且残差分布区域更集中。

2) 只要公共点在3个以上,无论其数目多少,附有参数的条件平差模型的验后单位权中误差σ0均明显优于间接平差模型,其σ0值约为间接平差模型的1/3到2/3.

[1] 姚吉利.3维坐标转换参数直接计算的严密公式[J].测绘通报,2006(5): 7-10.

[2] 张皓琳,林嘉睿,邾继贵.三维坐标转换精度及其影响因素的研究[J].光电工程,2012,(10):26-31.

[3] 王解先,季凯敏.工业测量拟合[M].北京:测绘出版社,2008.

[4] 王穗辉.误差理论与测量平差[M].上海:同济大学出版社,2010.

Three-Dimensional Coordinate Transformation Model by Simultaneously Considering Both Pre-and Post-transforming Coordinate’s Error on Common Sites

WANG Ahao1,2,WANG Jiexian1,CHEN Junping2,3

(1.CollegeofSurveyingandGeo-Informatics,TongjiUniversity,Shanghai200092,China;2.ShanghaiAstronomicalObservatory,ChineseAcademyofScience,Shanghai200030,China;3.ShanghaiKeyLaboratoryofSpaceNavigationandPositioningTechnology,ChineseAcademyofScience,Shanghai200030,China)

Traditional three-dimensional coordinate transformation method, estimates seven transformation parameters,namely the translate, rotation and scale parameter, using conventional least square estimator. It considers only the coordinate error of the common sites in the transformed coordinate system. In fact, station coordinates in both coordinate systems may have errors, and the mis-modelling of such error may lead to bigger uncertainty of the estimated parameters. This paper considers the station coordinates error of the common sites in both systems, and applies the conditional adjustment model for parameter estimation. A local GPS network is used to test the new model. The magnitude distribution histogram of the coordinate transformation residuals shows that the residuals from the new model is more concentrated around zero, and its distribution area is significantly smaller than that of the traditional model. Also, the mean square error of unit weight of the new model is about 1/3 to 2/3 in the order of the traditional model.

Coordinate transformation; seven parameters; parameter adjustment; condition adjustment with parameters; residual; mean square error of unit weight

10.13442/j.gnss.1008-9268.2016.05.012

2016-06-12

P228.4

A

1008-9268(2016)05-0061-05

王阿昊 (1992-),男,硕士生,主要从事卫星大地测量方面研究。

王解先 (1963-),男,博士,教授,博士生导师,主要从事卫星大地测量方面的研究工作。

陈俊平 (1980-),男,博士,研究员,博士生导师,主要从事卫星大地测量研究与应用。

联系人： 王阿昊 E-mail: bdserwah@tongji.edu.cn