遗传算法求解变循环发动机稳态性能参数研究

伍建伟,刘夫云,甘 林,邓 勇

(桂林电子科技大学 机电工程学院,广西 桂林 541004)



遗传算法求解变循环发动机稳态性能参数研究

伍建伟,刘夫云,甘 林,邓 勇

(桂林电子科技大学 机电工程学院,广西 桂林 541004)

以双涵道变循环发动机为研究对象，在一定简化条件下采用部件级建模法在MATLAB平台上建立了整机的稳态数学模型，开发了该模型的求解程序进行数值仿真。为求得满足平衡方程和约束条件下稳态发动机的性能参数，将发动机性能参数作为设计变量，平衡方程相对偏差的和作为目标函数，用遗传算法(GA)对加入插值法出错机制的模型进行求解。计算结果表明：在GA程序中加入出错处理机制的程序，可有效解决多连通、小范围连续的可行域，以及插值法产生的问题，进而求得该工况下的稳态发动机性能参数。

变循环发动机； 部件级建模法； 数值仿真； 平衡方程； 目标函数； 遗传算法； 插值法； 稳态性能参数

0 引言

目前，燃气涡轮发动机占据航空动力的主导地位，是知识密集、军民两用的高科技产品，是国家科技工业水平和综合国力的重要标志，成为各大国大力发展、高度垄断的关键技术[1]。由飞机/发动机设计原理可知：对持续高马赫数飞行任务，需要高单位推力的涡喷循环；反之，如任务强调低马赫数和长航程，就需要低耗油率的涡扇循环[2-3]。变循环发动机(VCE)可同时具备高速时的大推力与低速时的低油耗，这使它有强大的性能优势，受到各航空强国的重视，成为目前航空发动机的重要研究方向。

目前，国内关于变循环发动机的研究处于探索阶段，主要集中在发动机整机建模和模式切换过渡仿真、稳态性能模拟，以及总体结构初步设计等方面[4-8]。文献[4]建立了变循环发动机整机数学模型，研究了变循环发动机相关参数对模式转换的影响，通过数值仿真得出了与实际相符的结论，即双涵工作模式下发动机耗油率低，适于亚声速巡航飞行，单涵工作模式下发动机单位推力高，适于超声速巡航飞行。文献[7]对变循环发动机进行了数值模拟，研究了变循环发动机的高度、速度和低压转速对推力、耗油率、涵道比、前涵道比和后涵道比的影响，并得出结论：相较于单外涵模式，双外涵模式的单位推力和耗油率低，其受飞行条件影响的主要为前涵道比。文献[8]给出了变循环发动机总体结构的初步方案，并对模式转换机构进行了性态分析，确定了该方案的可行性。文献[9]对变循环发动机建模方法进行了研究及验证。但有关求解的方法及其求解效率的研究较少。文献[10]提到了用Newton-Raphson法求解变循环稳态模型，但该法有两方面的缺陷：一是需要初始点，即文献[4-5、7]提及的“初猜值”，而实际上，随意猜得的值很可能落入插值范围之外，在迭代中会出现超出插值范围的错误；二是该法易陷入局部最优点，这是传统优化算法的通病，对本文研究的多连通、小范围连续的可行域及含插值法的问题，则更易陷入局部最优。国内外，多位学者用GA对航空发动机进行了优化设计[11-12]。虽有提到用改进的混合粒子群算法对变循环发动机模型进行求解，但并未涉及关于含插值法(利用重要部件实验特性数据时使用的方法)问题的解决方案[13]。为此，本文在建立变循环发动机双涵道数学模型的基础上，分析了该模型适用的条件、适用的范围，加入了插值法出错处理的机制，并用遗传算法进行数值仿真。

1 MATLAB与遗传算法简介

MATLAB是一套高性能数值计算和可视化软件，集成数值分析、矩阵运算、信号处理和图形显示于一体，在系统建模和仿真、科学和工程绘图及应用程序开发等领域有广泛应用[14]。MATLAB也是一种专业的计算机程序，用于工程科学的矩阵数学运算。MATLAB 程序执行MATLAB 语言，并提供了一个极其广泛的预定义函数库，可使相关技术工作变得简单高效。同时， MATLAB拥有强大的调试功能，能在建模过程中方便发现错误、改正错误。因此，本文用MATLAB语言编制程序，可提高建模的效率和质量。与此同时，随着MATLAB软件版本的升级，函数库进一步丰富完善，并加入了基于遗传算法的优化函数，用于处理复杂的大型优化问题。

GA是借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索算法，适用性广，特别适于处理传统方法处理效果不佳的复杂和非线性问题[15-18]。最优化问题是其经典应用领域，但传统方法在有效解决大规模、多峰态、函数、含离散变量等问题时往往存在许多障碍。作为一种新的全局优化搜索算法，GA因其简单易用，对很多优化问题能较易地解出令人满意的解，不仅适于传统优化问题，而且适于非线性方程组的求解[17-18]。基于以下因素，本文选择GA进行优化。

a)GA适于数学关系不明确的问题。考虑发动机的部件较多，在建立的发动机模型中，发动机性能参数并不直接与平衡方程相关联，即待求变量与平衡方程间的数学关系并不明确。GA仅使用问题本身的目标函数值，无需其它任何先决条件和辅助信息，所用有关特定问题的信息非常少。

b)GA无需输入初始点，而是随机产生初始种群。GA以群体为基础，不是以单点搜索为基础，能同时获得多个峰值，因此陷入一个局部最小的可能性明显减小。对本文建立的模型，可行域呈现为多连通、小范围连续的性质，如采用传统优化算法，受到初始点的限制，极易陷入局部最优。

c) 现行非线性优化算法多基于线性、凸性、可微性等, 但GA无相关假设。GA只需要评价目标值的优劣, 应用性较广，能较好地求解本文研究的数学模型。

d)GA具随机性特点，是一种渐近式趋于最优的近似算法。GA在每次的迭代过程中，利用复制、交换、突变等操作，使下一代的结果大体上优于上一代。本文在双涵道变循环发动机建模时作了一定的简化，建立的模型是一种近似模型，无需求得精确解。另外，随着种群和迭代代数的增加，GA的解会趋于精确解。

2 变循环发动机双涵道模式稳态模型建立

2.1 变循环发动机构造及其原理

本文研究对象是双涵道变循环发动机，主要部件包括进气道、风扇、副外涵道、核心驱动风扇级(CDFS)、CDFS涵道、主外涵道、前混合器、高压压气机、主燃烧室、高压涡轮、低压涡轮、后混合器、加力燃烧室，以及尾喷管等[4-7]。双涵道模式下，选择活门和后混合器(后VABI)全部打开；单涵道模式下，选择活门关闭，后混合器关小至一定位置。文献[10]给出了发动机的具体结构。

变循环发动机的工作原理如图1所示。其工作模式有涡喷和涡扇两种。发动机在亚声速巡航的低功率工作状态，风扇后的模式转换活门因为副外涵与风扇后的压差打开，使更多空气进入副外涵，同时前混合器面积开大，打开后混合器，增大涵道比，降低油耗，此时为发动机的涡扇模式。发动机在超声速巡航、加速、爬升状态时，前混合器面积关小，副外涵压力增大，选择活门关闭，迫使绝大部分气体进入核心机，产生高的推力，此时为发动机的涡喷模式。

2.2 变循环发动机部件建模法

燃气涡轮发动机的特性可用实验方法或数值方法获得。但实验方法需研制复杂的设备、投入巨额的资金和消耗巨大的能源，因此逐渐被数值模拟方法替代。随着计算能力的不断提高，发动机数学模型研究的不断深入，计算机仿真精度在不断提高，一定程度上弥补了实验方法的不足，尤其是在发动机研制过程中，燃气涡轮发动机计算机仿真技术发挥了不可替代的作用。

燃气涡轮发动机由进气道、压气机、主燃烧室、涡轮、喷管等部件组成。如计算机能对这些部件的性能进行准确的模拟，就能准确地模拟整个发动机的性能。这种建立在准确模拟发动机各部件性能基础上的发动机性能计算方法，被称为部件法。该法是建立在发动机各部件特性已知的基础上，因此计算精度较高[4]。本文利用压气机、涡轮的特性数据，采用线性插值法计算相应的换算转速、增压比(落压比(对涡轮而言))、效率，以及换算流量。

2.3 建模前模型假设

变循环发动机是十分复杂的气动热力学系统，建立其精确的数学模型十分困难。因此，本文在建立其非线性部件级模型时，作以下适当简化：

a)忽略燃油在燃烧室中燃烧延迟的影响；

b)气流在各部件的流动均按准一维流动处理；

c)不考虑流入流出时的放气量[19]。

2.4 变循环发动机双涵道模式稳态数学模型

2.4.1 发动机性能参数

变循环发动机的性能参数有12个：nL为低压转速(风扇、低压涡轮物理转速)；nH为高压转速(高压压气机、CDFS、高压涡轮物理转速)；ZCL为风扇压比函数值；ZCDFS为CDFS压比函数值；ZCH为高压压气机压比函数值；T4*为主燃烧室出口温度；ZTH为高压涡轮压比函数值；ZTL为低压涡轮压比函数值；αL为风扇导叶角；αCDFS为CDFS导叶角；αH为高压压气机导叶角；αCH为低压涡轮导叶角。

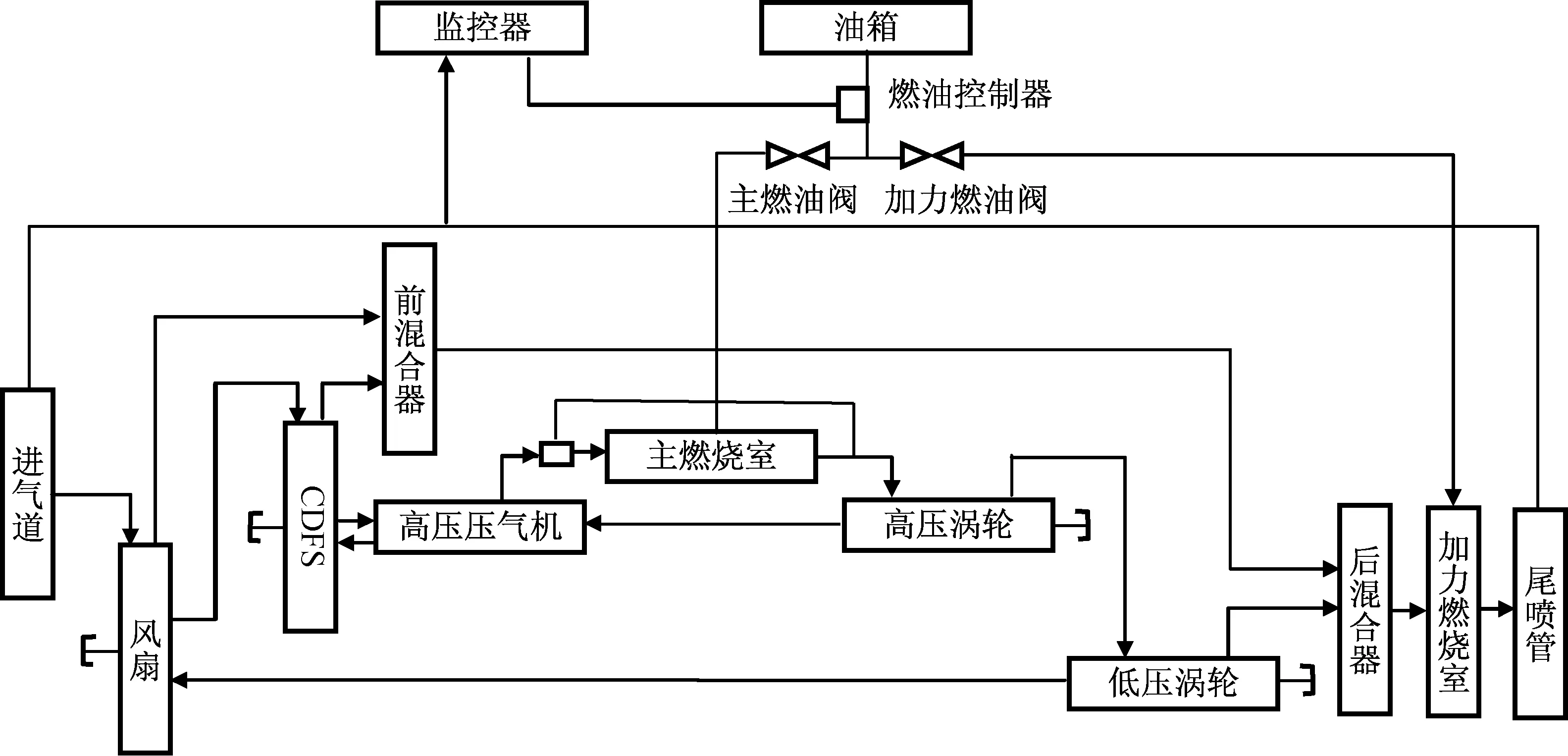
图1 变循环发动机工作原理Fig.1 Principle of variable cycle engine

2.4.2 求解工况

在发动机飞行高度H=11 km，飞行马赫数Ma=0.8的亚声速巡航点，采用双涵道模式，导叶角度均设置为0°。在该典型工况下，选择活门完全打开，取副外涵道面积1.839103，后混合器出口总面积2.851 8104，尾喷管喉道面积9.554 4103。由满足的方程和条件，求解在该工况下稳态时的发动机性能参数。

2.4.3 双涵道模式稳态数学模型建立

首先，根据变循环发动机的计算公式，构造各部件相应的数学模型，用MATLAB程序语言编制各部件函数，建立各函数的流入该部件与流出该部件参数间的关系[10]。各部件对应的M文件如下：inlet.m为进气道函数；compressor.m为风扇、CDFS和高压压气机函数(其中最后的一个输入参数num 1，2，3分别对应风扇、CDFS和高压压气机的计算)；main_combusition_chamber.m为主燃烧室；turbine_H_and_L.m为高压涡轮与低压涡轮函数(其中最后的一个输入参数num 1，2分别对应高压涡轮和低压涡轮的计算)；forward_mixer.m为前混合器函数；rear_mixer.m为后混合器函数；exhaust_nozzle.m为尾喷管函数。

然后，建立整机模型函数(M文件为whole_machine_model_fun.m)、整机的目标函数(M文件为obj_fun.m)，以及其约束函数(M文件为non_con_fun.m)。其中：整机的稳态模型函数是对各部件气体流入流出的一个模拟，是对各部件数学模型的有机组合；约束函数是在插值需满足的限制条件及流动气体在通过各部件时的限制条件(如流经CDFS的流量大于高压压气机的流量，因为流出CDFS的流量会部分流入主涵道)；整机的稳态模型函数和约束函数的输入变量为发动机的性能参数(考虑求解工况下将导叶角设置为0°，故此时待求的发动机的性能参数为8个)。

最后，用MATLAB优化工具箱中的遗传算法函数进行求解，流程如图2所示。

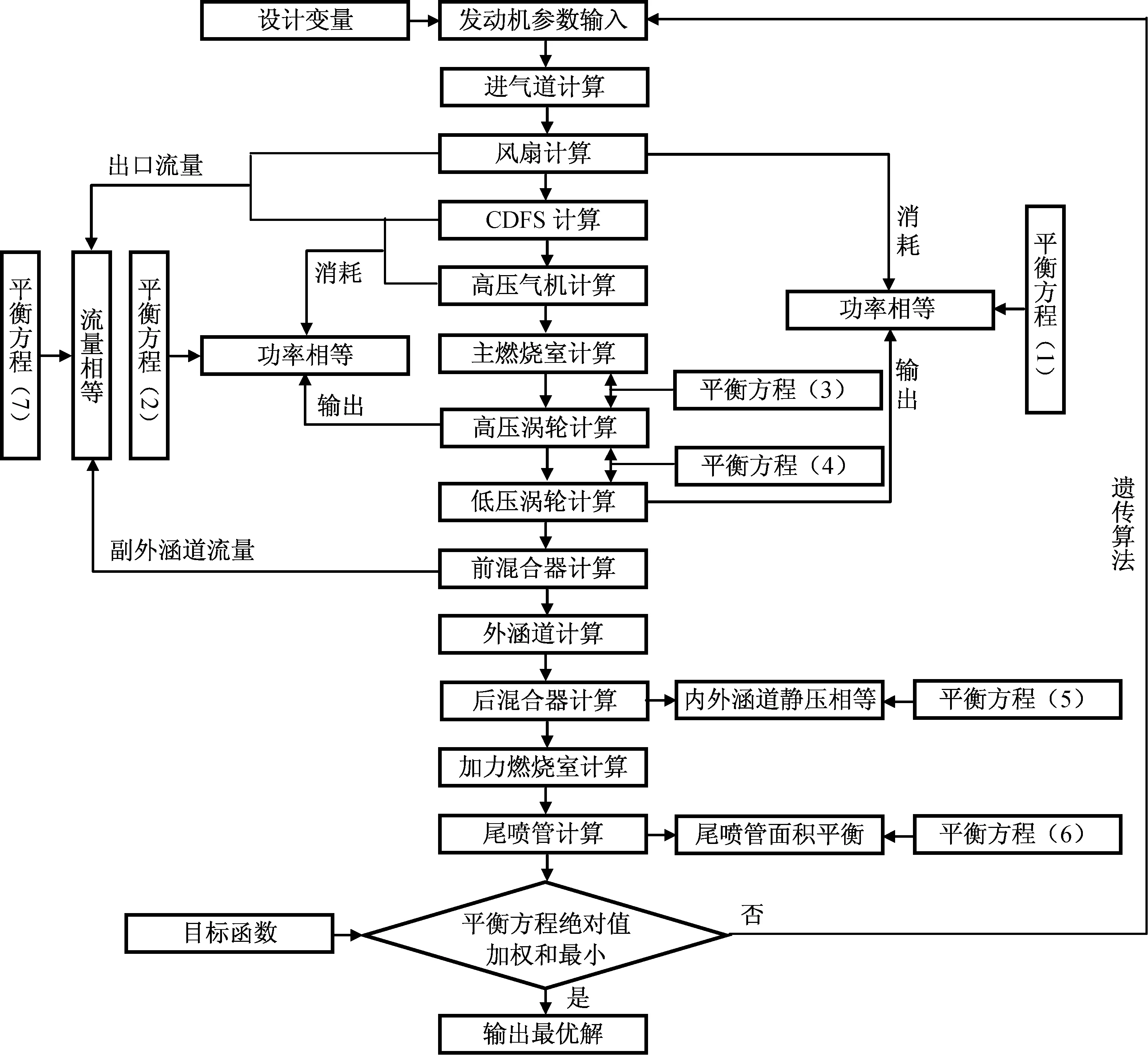
图2 双涵道变循环发动机建模及求解流程Fig.2 Flowchart of modeling and solving for double bypass variable cycle engine

2.4.4 发动机平衡方程

发动机匹配工作时，受以下平衡方程制约[10]。

a)低压轴功率平衡

NCL-NTLηmL=0.

(1)

式中：NCL为风扇消耗功率；NTL为低压涡轮发出功率；ηmL为中间轴机械效率，取ηmL=0.99。

b)高压轴功率平衡

NCH+NCDFS-NTHηmH=0.

(2)

式中：NCH，NCDFS分别为高压压气机和CDFS的消耗功率；NTH为高压涡轮发出功率；ηmH为高速轴机械效率，取ηmH=0.99。

c)高压涡轮进口截面流量平衡

(3)

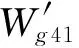
d)低压涡轮进口截面流量平衡

(4)

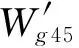
e)后混合器静压平衡

p61-p62=0.

(5)

式中：p61，p62分别为后混合器内、外涵道(主外涵道)的静压，两者应平衡。

f)尾喷管面积平衡

(6)

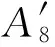
g)风扇出口流量平衡

Wa2-Wa21-Wa13=0.

(7)

式中：Wa2为风扇出口流量；Wa13为副外涵流量；Wa21为CDFS进口流量，三者间存在平衡关系。其中：Wa13由文献[10]中前混合器的有关公式算出。

3 遗传算法求解前模型处理

3.1 平衡方程求解转为优化问题处理

本文已知飞机在某种典型工况，在满足平衡方程和约束条件下，求解变循环发动机的性能参数。为便于用MATLAB自带的遗传算法函数ga进行求解，可作如下处理：发动机性能参数作为设计变量；平衡方程相对偏差之和作为目标函数(即GA的适应度函数)；约束条件(插值点的范围及气体流经发动机各部件所满足的关系)提取出建立非线性约束函数。

GA是利用一定的寻优规则，改变或调节输入参数(发动机性能参数)值，使目标函数达到最优。由于目标函数是平衡方程的加权和(也称为相对偏差之和)，当该目标函数最小，即最接近于0时，等价于满足平衡方程，此时的最优解即为平衡方程的解。

3.2 插值方法计算出错处理

本文建立的发动机整机模型有一定的复杂性，为能充分利用实验获得重要部件的特性数据，部分中间变量求解采用了插值方法。双涵道变循环发动机的数学模型转为优化问题后，受约束条件及插值范围的限制，可行域呈现为多连通、小范围连续的性质。因此，如直接利用GA寻优，因要求使用的点必须在插值的范围内，若超出插值范围则计算中出错，势必导致算法中止。为避免此情况的出现，在整机模型的程序中加入了错误捕捉命令(在稳态模型程序中加入MATLAB的try-catch语句)，当出现错误，可判定此解不满足条件，进而进入下一次迭代寻优。

4 GA求解结果与分析

在MATLAB开发平台编制相应的程序，用GA求解给定工况下的VCE整机的数学模型，结果见表1。

计算结果分析如下。

a)求解过程

在GA求解过程中，设置了3组迭代的代数和初始种群个数。由表1可知：当迭代数和初始种群数较小时，GA陷入了局部最优解。随着迭代数和初始种群数的增加，目标函数值进一步减小，求解的结果进一步精确。但随着迭代数和初始种群的进一步增加，目标函数值减小的幅度相当小，其值已基本接近于0，表明该优化结果已收敛于该点。考虑GA是一种全局寻优的算法，故可知该点为全局最优点。

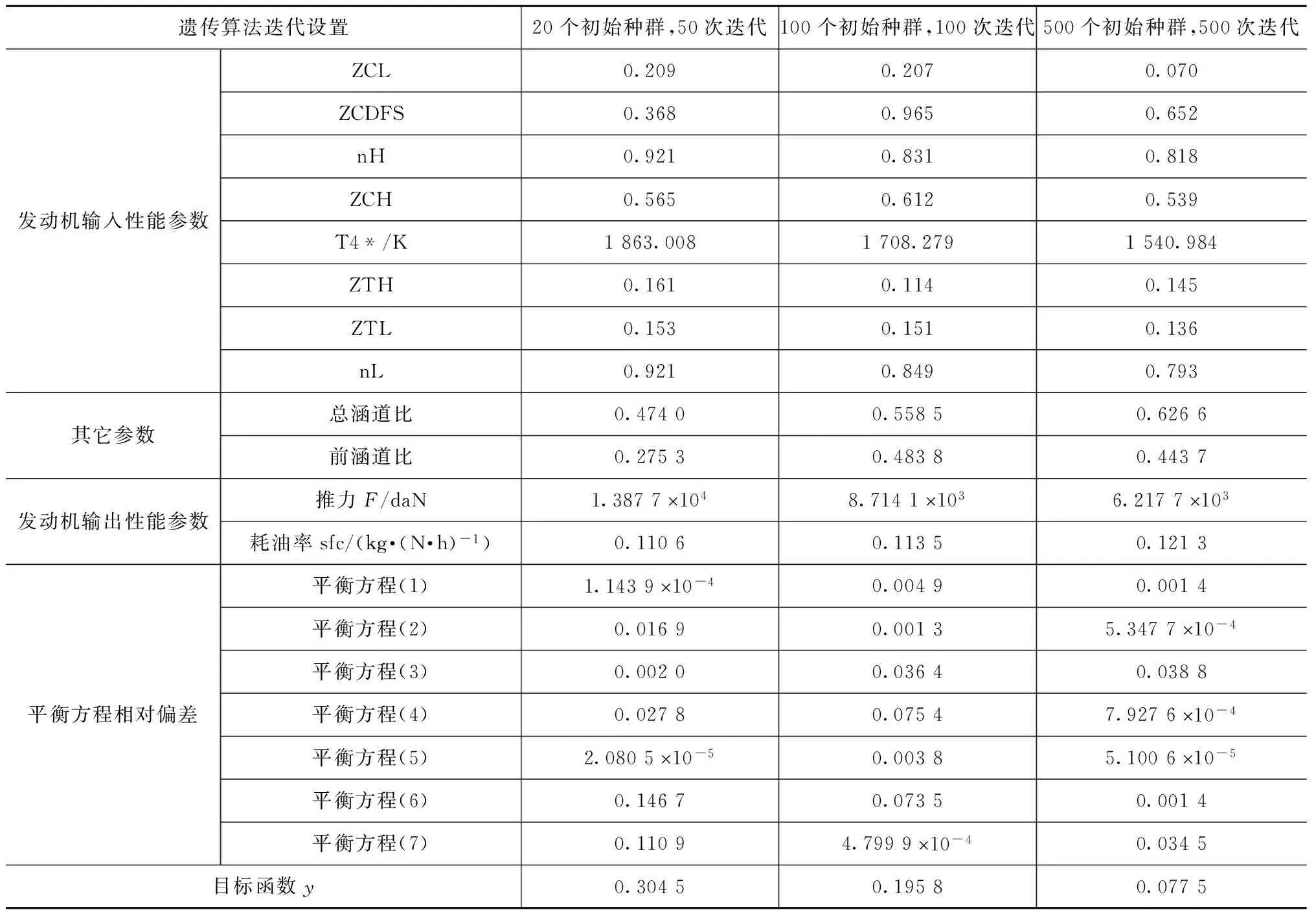
表1 遗传算法求解双涵道模式结果

b)求解结果

第三个迭代设置求解的结果表明，平衡方程式(3)、(7)的相对偏差值较大，分别为3.88%，3.45%，而其他平衡方程的相对偏差均小于0.2%，满足平衡方程。考虑本文建立的模型是理想状况，也是近似的，因此存在一定的误差可接受。由图2可知:平衡方程式(3)是高压涡轮进口截面流量平衡，而平衡方程式(7)是风扇和CDFS总的流量与副外涵道流量的平衡。由于建模前的假设(不考虑流入流出时的放气量)，故这两个平衡方程的相对偏差值相对较大，但均在4%以内，这是合理的。上述结果及求解的中间数据与文献[4-5、7-8]的数据基本一致，可断定此解即为该工况下双涵道模式的稳态仿真结果。

5 结束语

本文以变循环发动机的双涵道模式为研究对象，将平衡方程的求解转化为优化问题的求解策略，利用插值方法出错处理机制，解决了变循环发动机稳态性能参数的求解问题。特别是程序中使用的插值方法出错处理，即采用错误抛出命令(try catch)，这样可控制程序中的错误，避免在寻优的过程中程序中断。研究获得了以下结果：本文用GA求解变循环发动机稳态性能参数，可有效解决多连通、小范围连续的可行域及插值法产生的问题，进而求得该工况下的稳态发动机性能参数。后续将本文的处理方法用于发动机性能参数的优化，将发动机的其它参数(如导叶角、副外涵道面积、后混合器出口面积和尾喷管面积)作为设计变量，以耗油率和推力作为目标函数，用GA对目标函数进行优化，在保证满足平衡方程和约束条件的前提下，获得发动机最优性能。

[1] 刘大响, 金捷. 21世纪世界航空动力技术发展趋势与展望[J]. 中国工程科学， 2004, 6(9): 1-8.

[2] 方昌德. 变循环发动机[J]. 燃气涡轮试验与研究. 2004, 17(3): 1-5.

[3] 梁春华. 未来的航空涡扇发动机技术[J]. 航空发动机, 2005, 31(4): 54-58.

[4] 苟学中, 周文祥, 黄金泉. 变循环发动机部件级建模技术[J]. 航空动力学报, 2013, 28(1): 104-111.

[5] 王元, 李秋红, 黄向华. 变循环发动机建模技术研究[J]. 航空动力学报, 2013, 28(4): 954-960.

[6] 周红, 王占学, 张晓博, 等. 变循环发动机模态转换的几何调节规律[J]. 航空动力学报, 2015, 30(9): 2160-2166.

[7] 刘增文, 王占学, 黄红超, 等. 变循环发动机性能数值模拟[J]. 航空动力学报, 2010, 25(6): 1310-1315.

[8] 刘洪波, 王荣桥. 变循环发动机总体结构和模式转换机构研究[J]. 航空发动机, 2008, 34(3): 1-5.

[9] 王元, 张平平, 李秋红, 等. 变循环发动机建模方法研究及验证[J]. 航空动力学报, 2014, 29(11): 2643-2651.

[10] 苟学中. 变循环发动机建模及控制规律研究[D]. 南京: 南京航空航天大学, 2012.

[11] ZHAO J, XU M. Fuel economy optimization of an Atkinson cycle engine using genetic algorithm[J]. Applied Energy, 2013, 105: 335-348.

[12] 李立君, 尹泽勇, 乔渭阳. 基于多目标遗传算法的航空发动机总体性能优化设计[J]. 航空动力学报, 2006, 21(1): 13-18.

[13] 白洋, 段黎明, 柳林, 等. 基于改进的混合粒子群算法的变循环发动机模型求解[J]. 推进技术, 2014, 35(12): 1694-1770.

[14] CHAPMAN S J. Matlab programming for engineers[M]. Wadsworth: Wadsworth Publishing, 2007.

[15] HOLLAND J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. Michigan: U Michigan Press, 1975.

[16] GOLDBERG D E. Genetic algorithms in search, optimization and machine learning[M]. New Jersey: Addison-Wesly, 1989.

[17] KAVOUSI A, VAHIDI B, SALEHI R, et al. Application of the Bee algorithm for selective harmonic elimination strategy in multilevel inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1689-1696.

[18] 胡斐, 赵治国. 基于MATLAB的非线性方程组遗传解法[J]. 计算机时代, 2010, 28(3): 44-45.

[19] 周文祥. 航空发动机及控制系统建模与面向对象的仿真研究[D]. 南京: 南京航空航天大学, 2006.

Study on Solving Steady-State Performance Parameters for Variable Cycle Engines with Genetic Algorithm

WU Jian-wei, LIU Fu-yun, GAN Lin, DENG Yong

(Mechanic and Electronic Engineering, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China)

A steady mathematical model of double by pass variable cycle engine (VCE) was constructed under certain simplified conditions by using component-level modeling based on MATLAB. The solver was developed to finish numerical simulation. In order to solve the steady-state performance parameters of the engine under the equilibrium equation and constraint conditions, the engine performance parameters were selected as design variables, and the relative deviation of the equilibrium equation was selected as objective function. The genetic algorithm was used for solving the model added error mechanism of the interpolation method. Results show that the genetic algorithm program with the error handling mechanism can effectively figure out the troubles of the multiply connected and small scale continuous feasible region as well as the problems brought by the interpolation method. In this way, the steady-state engine performance parameters are solved under this working condition.

Variable cycle engines; Component-level modeling; Numerical simulation; Equilibrium equation; Objective function; Genetic algorithm； Interpolation method; Steady-state performance parameters

1006-1630(2016)05-0077-07

2016-04-21；

2016-07-06

国家自然科学基金资助(51265006)；广西科技开发项目(桂科攻1598007-51)；柳州市科技开发项目(2013H020401)

伍建伟(1989—)，男，硕士生，主要研究方向为机械动力学与优化算法研究。

V231

A

10.19328/j.cnki.1006-1630.2016.05.012