基于遗传算法的网格化球顶相控阵波束综合

杨正龙，张 锐，杨文军，黎海林

(1. 南京电子技术研究所, 南京 210039)(2. 北京跟踪与通信技术研究所， 北京 100094)



·天馈伺系统·

基于遗传算法的网格化球顶相控阵波束综合

杨正龙1，张 锐1，杨文军1，黎海林2

(1. 南京电子技术研究所, 南京 210039)(2. 北京跟踪与通信技术研究所， 北京 100094)

与传统平面相控阵波束综合方式不同，共形相控阵天线单元指向不一，阵列方向图难以表达成阵因子和单元因子的乘积形式。针对二维共形相控阵列波束综合问题，建立了一种网格化球顶相控阵列几何描述模型，推导了包含单元方向图的波束形成与计算公式。基于遗传算法，采用幅度加权方式，以阵列波束副瓣电平、指定方向陷零等指标作为代价函数，对阵列方向图进行了优化，优化后的最大副瓣电平达-23dB，指定方向陷零可达-75dB。仿真实验验证了波束形成及优化算法的正确性，相关算法技术可推广应用于不同形式的共形阵列波束综合。

共形阵；网格化球顶相控阵；遗传算法

0 引 言

随着雷达技术的不断发展，有源相控阵天线凭借其波束扫描捷变、动态范围大、搜索跟踪能力强等特点，已成为各种雷达设计主流。在一些特定应用场合，需采用共形相控阵天线，比如在机载、弹载雷达用途中，天线阵面可与平台表面共形安装，以保证载机的气动外形[1]；在舰载雷达中，一套共形阵列天线，不仅能替代传统多面阵的战区监视覆盖，还能最大限度地利用有限安装空间，扩展阵面口径；在地基雷达应用中，球顶构型的共形阵可覆盖整个半球空域，在多目标卫星测控、临近空间目标监视等领域有着广阔的应用前景。

同传统平面相控阵不同，共形相控阵天线的单元指向不一，阵列方向图难以表达成阵因子和单元因子的乘积形式，波束综合及优化相对复杂。在地面大型共形阵列的工程实践中，网格化球顶相控阵体制，将整个球顶进行栅格化，具有“全局球面、局部平面”的特点。网格化的球顶相控阵具备以下优势：首先，波束形成方法简化，共形子阵内可借鉴传统算法，共形子阵间进行程差、单元方向图以及极化补偿[2]；其次，阵面口径资源管控以子阵为单位，易于实现子阵级滑窗重构与电扫，完成全空域覆盖；最后，局部平面化后，不同形状的子阵模块种类较少，且对有源子阵后端的剖面要求降低，增强了其工程可实现性和维护性[3]。

阵列方向图综合有许多方法，如经典的Dolph-Chebyshev法和Taylor线源法，共形阵方向图优化可采用交替投影法[4]、粒子群算法[5]以及遗传算法[6-9]等。由于遗传算法对典型的非线性多维优化问题的求解通用性较强，已被广泛的应用于共形阵列方向图优化之中。针对环形阵方向图综合及陷零，共形阵方向图优化中的互耦考虑以及GA算法的代价函数选取等专门性问题，均开展了相应研究，但针对网格化球顶相控阵体制，且考虑天线单元方向图的波束综合及陷零方法，仍需开展进一步的研究。

本文介绍了一种网格化球顶相控阵实现模型，在此基础之上推导了包含单元方向图的波束形成公式；采用遗传算和幅度加权方式对共形阵面波束进行了最大副瓣优化及指定方向陷零；仿真试验验证了波束形成及优化算法的正确性。

1 网格化球顶相控阵波束形成

1.1 网格化球顶阵模型

一种工程可实现的网格化球顶相控阵天线模型如图1所示。

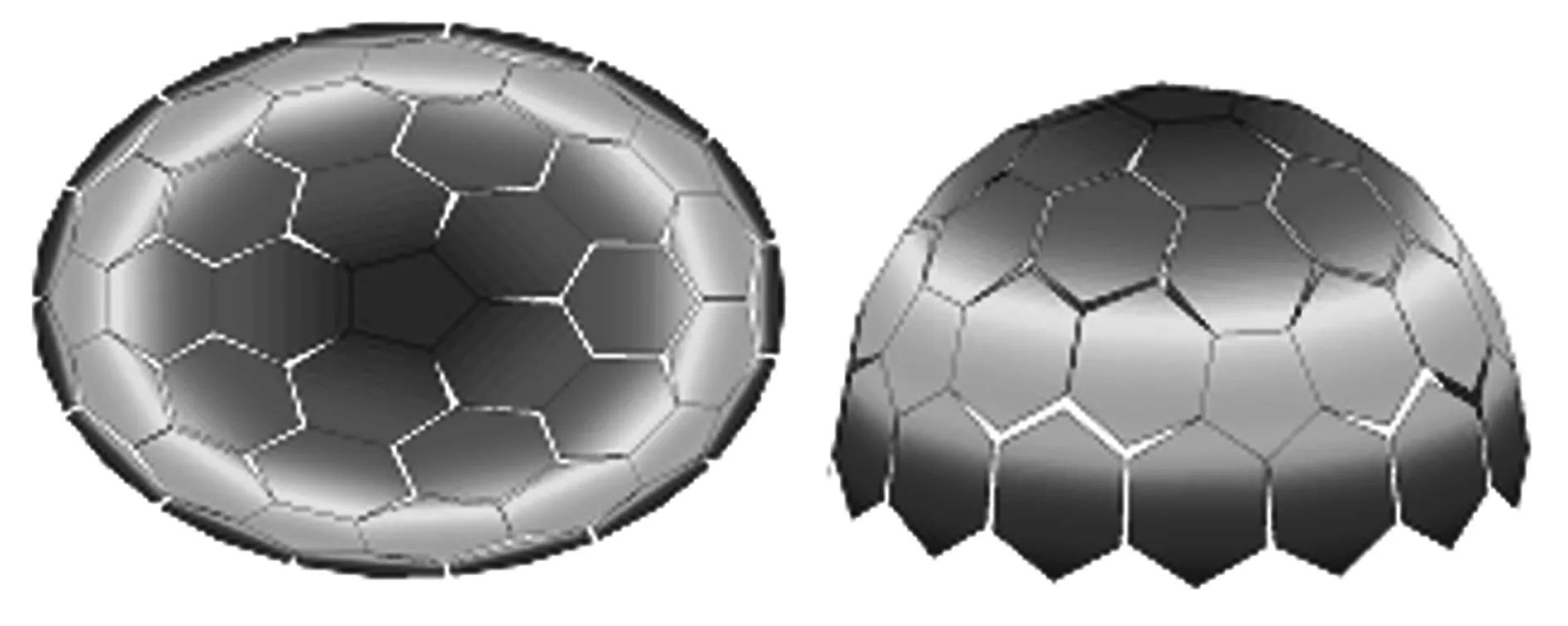
图1 网格化球顶相控阵模型

阵面采用改进的足球烯结构，全阵面由46块边长相等的五边形和六边形子阵构成，其中，五边形6块，六边形40块。共形子阵面可通过组合方式形成波束。记第i块子阵面为pi，则该子阵面的空间位置可描述为

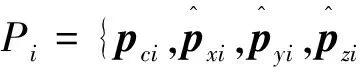
(1)

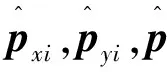
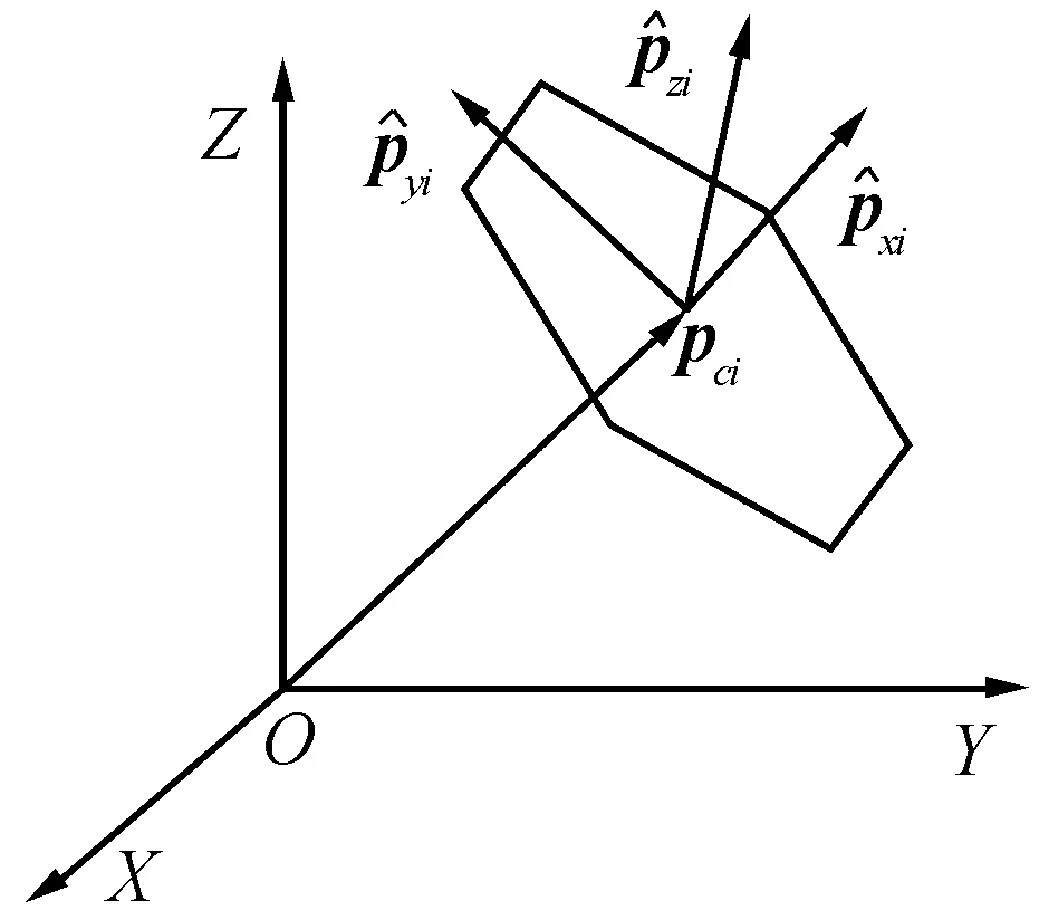
图2 子阵面几何关系

j=1,2,3,…,N}

(2)

式中：acij为第i个子阵面中第j个单元的中心坐标，且有

(3)

1.2 网格化波束形成方法

(4)

各单元移相值为

(5)

Φij= Φ1+Φ2=

(6)

其中

(7)

(8)

若考虑等幅度加权，则式(8)可化为

(9)

由式(9)可知，在网格化球顶相控阵体制下，单元方向图主要影响阵间幅相补偿，不影响阵内幅度加权；一般的网格化球顶相控阵波束方向图难于解析表达，可通过式(9)进行仿真计算及优化。全局方向图转换为单元方向图的公式为

(10)

2 基于遗传算法的波束综合优化

2.1 遗传算法原理

遗传算法是模拟自然界中“生存竞争，适者生存”的准则，在解决大空间、非线性、全局最优等复杂问题时，具有传统算法所不具备的独特优点。近十年来，利用遗传算法在电磁场与天线设计中的应用也非常多，主要用于阵元位置，激励电流幅相的寻优，以达到低副瓣[10]、特定角度置零等目的。

由于共形相控阵天线方向图难以解析表示，若严格考虑单元方向图影响，则应用传统窗函数及时频域变换理论则更为困难。而遗传算法则为一般的共形相控阵天线幅度加权优化，提供了一种较为通用的解决框架，其一般流程如图3所示。

图3 遗传算法基本流程图

2.2 基于遗传算法的波束优化

传统遗传算法大多以线阵为例，进行波束优化仿真，在应用遗传算法在共形阵列方向图的仿真优化过程中，大多也未考虑单元方向图的影响。本节在前述推导的基础上，时域计算网格化球顶相控阵天线的远场方向图，计算过程中，考虑单元方向图的影响，并采用遗传算法对波束进行幅度加权及优化，具体步骤为：

(1)建立网格化球顶相控阵列几何模型，例如式(1)～式(3)所示；

(2)计算特定波束指向下的各单元移相值，例如式(5)～式(7)所示；

(3)染色体初始化权系数wij，并依照式(8)，计算特定剖面下的方向图；

(4)利用适应度函数评估总群中各染色体的适应度，并进行选择、交叉、变异步骤；

(5)循环进行遗传算法，直至满足算法退出条件。

退出条件包括：出现了满足适应度要求的个体，达到最大代纪数量或总群收敛。

在波束优化过程中，适应度函数选择为[11]

f(wij)= α|MSLL-SLVL|+

β|NULL_PAT-NLVL|+γNULL_STD

(11)

式中：MSLL为最高旁瓣电平；SLVL为要求旁瓣电平；NULL_PAT为平均陷零深度；NLVL为要求陷零深度；NULL_STD为陷零深度标准差；α,β,γ为权系数，可选择α=0.8,β=0.1,γ=0.1。如仅控制最大旁瓣，而无需陷零，可选择α=1,β=0,γ=0。

依据上述算法，可对网格化球顶相控阵的二维方向图进行优化，并考虑了单元方向图对阵列方向图的影响。

3 仿真试验与分析

3.1 仿真模型及参数

仿真模型为图1模型的球顶部分，包含1个五边形和5个六边形，其中，五边形子阵包括18个单元，六边形子包括36个单元，共计198个单元，如图4所示。

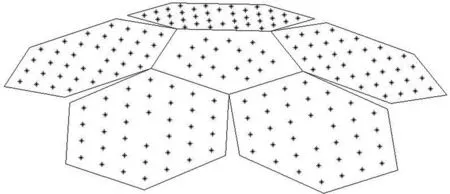
图4 仿真阵列模型

五边形单元间距为57.6 mm、66.5 mm，六边形单元间距为62.8 mm、72.5 mm，呈三角形排列，单元方向图如图5所示。

图5 单元方向图

分别选取极坐标下扫描角为(0°,0°)，(5°,0°)，(10°,15°)得到均匀权条件下，二维阵列方向图如图6所示。

图6 均匀权条件下的二维方向图

扫描角为(0°,0°)条件下，考虑单元方向图和未考虑单元方向图的一维阵列方向图如图7所示。

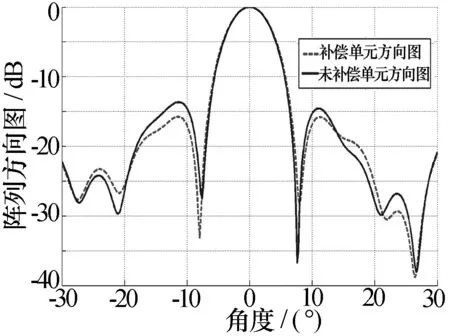
图7 考虑单元方向图影响下的阵列方向图

由图7仿真结果可见，考虑单元方向图的影响，补偿单元方向图时，最高副瓣为-15.76 dB，未补偿单元方向图时，最高副瓣为-13.67 dB，恶化约2.07 dB。遗传算法参数选择如表1所示。

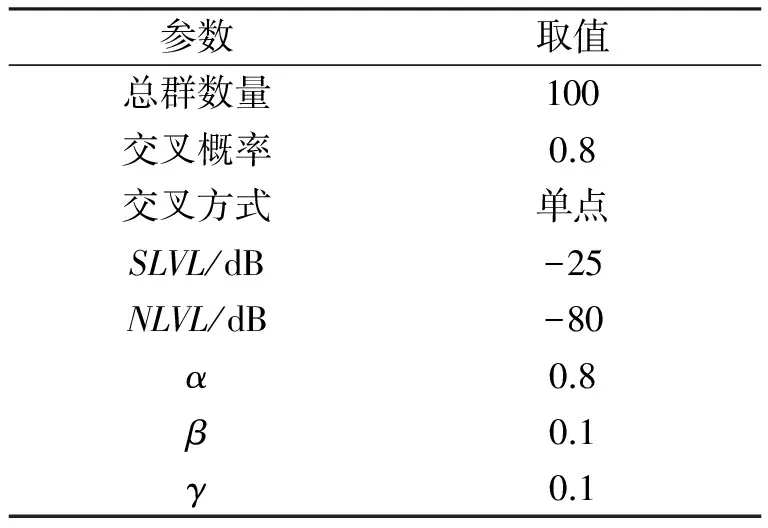
表1 遗传算法参数选择

3.2 仿真结果及分析

遗传算法迭代51代收敛，其中，个体最大副瓣水平收敛到-23 dB，总群最大副瓣水平收敛到-18 dB，如图8所示。

图8 遗传算法最大副瓣收敛曲线

利用遗传算法得到的幅度加权系数，优化前后XOZ剖面内的阵列方向图对比如图9所示。

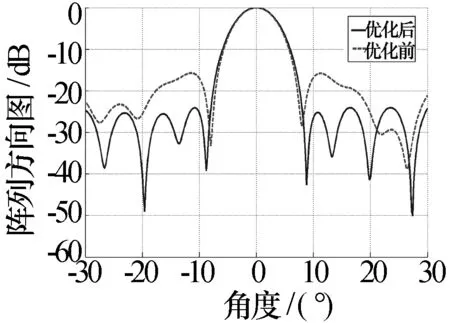
图9 优化前后阵列方向图(法向)

由图9可见，遗传算法能够较好的对阵列方向图进行优化，优化前后，最大副瓣电平降低-7 dB以上。对于扫描方向图，采用同一组优化权系数，仍能获得较好的波束综合效果，如图10所示。

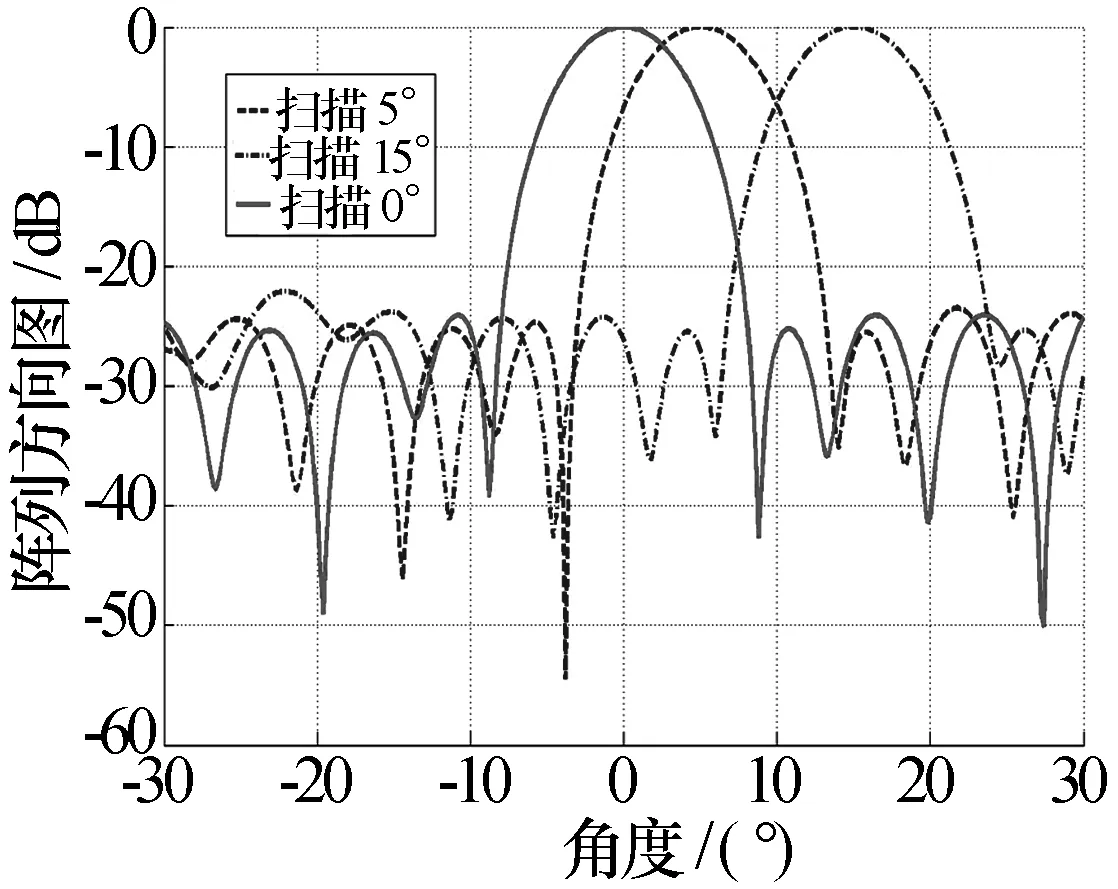
图10 优化前后阵列方向图(5°、15°扫描)

同时，进行最高副瓣控制及指定扫描角度为20°方向陷零，获得网格化球顶相控阵列方向图如图11所示。

图11 优化阵列副瓣并陷零(20°陷零)

由图11可见，使用遗传算法，针对网格化球顶相控阵天线，不仅可以完成最高副瓣控制，而且能够完成指定方向的副瓣陷零，增强系统抗干扰能力。

4 结束语

网格化球顶相控阵是一种工程可实现性较强的共形阵的实现形式，网格化后阵列移相算法可分为子阵内移相和子阵间移相两项，单元方向图的影响可归入子阵间因子。采用遗传算并考虑单元方向图影响，以最大副瓣电平最低以及指定方向陷零为适应度函数，优化得到了网格化球顶相控阵列的幅度加权系数，优化后最高副瓣为-23 dB，指定方向陷零达-75 dB。

[1] 齐飞林，刘 峥，杨明磊，张守宏, 等. 毫米波共形相控阵雷达引导波束形成[J]. 系统工程与电子技术，2009，31(8)：1874-1877. QI Feilin, LIU Zheng, YANG Minglei, et al. Low sidelobe beamforming for millimeter wave radar seeker with conformal phased array[J]. Systems Engineering and Electronics, 2009, 31(8): 1871-1877.

[2] DOHMEN C, ODENDAAL J W, JOUBERT J. Synthesis of conformal arrays with optimized polarization[J]. IEEE Transactions on Antennas and Propagation, 2007,55(10): 2922-2925.

[3] 张剑敏, 陈 钰, 余新华. 某机载设备结构总体设计[J]. 电子机械工程, 1997, 13(4): 10-19. ZHANG Jianmin, CHEN Yu, YU Xinhua. Design of an airborne equipment structural collectivity[J]. Electro-Mechanical Engineering, 1997, 13(4): 10-19.

[4] 陈 云，何炳发. 共形相控阵天线方向图综合[J]. 现代雷达，2008，30(12)：78-80. CHEN Yun, HE Bingfa. Pattern synthesis to conformal phased antenna[J]. Modern Radar, 2008, 30(12):78-80.

[5] 高 波，金荣洪，耿军平. 基于一种新的粒子群算法的天线方向图综合技术[J]. 电子与信息学报，2007，29(12): 3015-3019. GAO Bo, JIN Ronghong, GENG Junping. Pattern synthesis of antenna array using a novel quasi PSO algorithm[J]. Journal of Electronics & Information Technology, 2007, 29(12):3015-3019.

[6] ALLARD R J, WERNER D H, WERNER P L. Radiation pattern synthesis for arrays of conformal antennas mounted on arbitrarily-shaped three-dimensional platforms using genetic algotithms[J]. IEEE Transactions on Antennas and Propagation, 2003, 51(5): 1054-1062.

[7] 郭建明，刘 波，毛二可. 米波圆环天线阵的方向图综合研究[J]. 电波科学学报, 2008, 23(4): 792-796. GUO Jianming, LIU Bo, MAO Erke. Synthesis of circular array patterns of VHF band[J]. Chinese Journal of Radio Science, 2008, 23(4):792-796.

[8] 欧阳骏，杨 峰，聂在平，等. 基于遗传算法的载体上共形天线阵列优化[J]. 电波科学学报，2008, 23(2)：356-359. OUYANG Jun, YANG Feng, NIE Zaiping, et al. Optimizing design of conformal antennas array on platform with GA method[J]. Chinese Journal of Radio Science, 2008, 23(2):356-359.

[9] 曹 俊, 陈 敏, 宋志国. 用遗传算法实现平板裂缝天线功分网络布线设计[J]. 电子机械工程, 2006, 22(1): 33-35. CAO Jun, CHEN Min, SONG Zhiguo. The optimized design of the wiring of power dividing network of plate slotted array antenna using genetic algorithms[J]. Electro-Mechanical Engineering, 2006, 22(1): 33-35.

[10] 李东风，龚中麟. 遗传算法应用于超低副瓣线阵天线方向图综合[J]. 电子学报，2003,31(1)：82-84. LI Dongfeng, GONG Zhonglin. Application of genetic algorithms in the pattern synthesis of ultra-low sidelobe linear array antenna[J]. Acta Electronica Sinica, 2003,31(1):82-84.

[11] 范 瑜，金荣洪，刘 波，等. 阵列天线方向图综合中的遗传算法目标函数研究[J]. 电子与信息学报，2005, 27(5): 801-804. FAN Yu, JIN Ronghong, LIU Bo, et al. Study on the objective function for the array pattern synthesis based on genetic algorithm[J]. Journal of Electronics & Information Technology, 2005,27(5):801-804.

杨正龙 男，1976年生，博士后，高级工程师。研究方向为雷达系统总体、目标特性等。

张 锐 男，1982年生，博士，高级工程师。研究方向为共形相控阵雷达总体技术。

杨文军 男，1966年生，研究员级高级工程师。研究方向为相控阵雷达总体技术。

黎海林 男，1972年生，高级工程师。研究方向为雷达系统总体技术。

Radiation Pattern Synthesis for Geodesic Dome Phased Array Antenna Based on Genetic Algorithm

YANG Zhenglong1，ZHANG Rui1，YANG Wenjun1，LI Hailin2

(1. Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)(2. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)

Due to the different point directions of each radiation elements, the radiation pattern synthesis for conformal phased array is much different from the traditional plane phased array, and the array radiation pattern is not expressed as an analysis formula. This paper is focused on radiation pattern synthesis for 2 dimensional conformal array. Firstly, a mathematical model is established for geodesic dome phased array antenna and the expression of array radiation pattern is deduced accounting the element radiation pattern. Secondly, array pattern is optimized by using genetic algorithm, choosing the side lobe and depth of the notch as the price function, the maximal side lobe is below -23 dB and the notch of the designed direction is about -75 dB. Finally, the simulation experiments prove the proposed algorithms

conformal array; geodesic dome phased array antenna (GDPAA); genetic algorithm

10.16592/ j.cnki.1004-7859.2016.03.015

张锐 Email：94028691@qq.com

2015-10-16

2015-12-24

TN911.7

A

1004-7859(2016)03-0070-05