统计诊断理论用于航空发动机滑油系统故障诊断

王晓钢，刘振岗，郑宇，王玉才，邹刚

（1.海军航空工程学院青岛校区航空机械系，山东青岛266041；2.海军航空兵92543部队机务大队，山西长治046011）

统计诊断理论用于航空发动机滑油系统故障诊断

王晓钢1，刘振岗1，郑宇1，王玉才2，邹刚1

（1.海军航空工程学院青岛校区航空机械系，山东青岛266041；2.海军航空兵92543部队机务大队，山西长治046011）

某新型发动机滑油系统故障的统计判别诊断法，用人工智能方法及所建立的数值统计诊断理论模型，来判别发动机滑油系统的工作状态。最后结合具体故障案例，实现滑油系统故障的统计诊断，实践结果验证该方法诊断发动机滑油系统故障的正确性。

航空发动机；统计诊断模型；滑油系统EAM

0 前言

发动机就是飞机的心脏，滑油系统在整个发动机中起到极为重要作用，发动机工作时，轴承与传动齿轮等转动零件相互摩擦，会产生磨损和因过热而损坏［1］。为此，滑油系统可以将足够数量和适当黏度的清洁滑油，连续不断地喷到轴承和传动齿轮啮合处进行润滑，以减少摩擦，并带走因摩擦而产生的热量和赃物。滑油系统工作性能正常与否，将直接影响到发动机的工作性能及寿命，因此做好发动机滑油系统的故障诊断工作具有重大意义［2-3］。

统计诊断方法是近些年迅速发展起来的新的数值诊断方法。统计诊断是以统计学、概率论等数理统计知识为基石的，它是1964年由美国著名的控制论专家查德教授创立的［4］。因为发动机滑油系统故障症状可能由一种因素引起，亦可能由多种因素引起的，那么如何判断此时的发动机滑油系统工作性能正常与否，成为摆在故障诊断人员面前的首要任务。统计诊断法就是利用所建立起来的系统数值统计诊断理论模型，来判断发动机滑油系统的工作状态是否正常，进而实现对发动机故障的预报和诊断［5-6］。

1 统计数值诊断法概述

基于统计数学理论，建立统计数值诊断故障模型，运用最小冒险法及最小错误诊断概率法来判定发动机滑油系统污染临界值［7-8］，使专家经验分析有效的与定量分析、定性分析相结合，并将这一诊断过程应用在发动机滑油系统故障诊断中。实践结果证明，利用该模型来诊断故障的过程和结果更为合理准确［9］。

1.1 统计诊断数学模型的建立

这里以滑油油液污染分析为例，来介绍这种诊断方法。对油液污染进行分析时，无论用何种监测技术都有一个如何确定故障与非故障的临界值的问题。比如，若要求按照滑油料中的含铁量（以特征参数X表示）来诊断机器的状态，就需要对此参数确定一个临界值X0：当X＞X0时应当发出警告，令发动机停止工作；而当X＜X0时则可允许发动机继续工作。如果用D1表示机器的正常状态，用D2表示机器的异常状态，则上述规则可表达为式1。

因为发动机中所有摩擦零件如花键、齿轮等都会在润滑油中落入磨损残留物，因而滑油中的含铁量不能单值地表征发动机某一零件状态，如主轴承的状态。这样，由于一系列因素的影响，X值的分布规律对于处于正常状态下的轴承与磨损后的轴承来说，将会有重叠部分。图1。

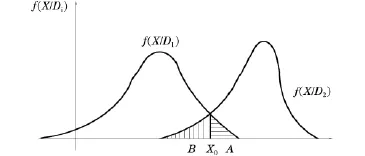
图1 滑油系统含铁量分布图

由于重叠部分的存在，按以上规则进行判决时必然会有发生判断错误的可能性。如果绝对不允许判断错误就无法选择临界值X0。所以问题归结为如何按照最佳条件的要求选择X0值。1.2错误判断的2种情况

（1）将正常状态D1错误地判断为异常状态D2（图1中A部分），这称为“谎报”。

（2）将异常状态D2错误地判断为正常状态D1（图1中B部分），这称为“漏检”。

以Hij（i，j=1，2）表示按决策规则式1，所可能采取的决策，下标“i”相当于诊断的状态，下标“j”相当于机器实际所处的状态。这样H11，H22就表示正确的诊断；H12表示漏检，H21表示谎报。

根据图1所示的决策规则进行诊断时可以由概率分布函数求出发生谎报的概率P（H21）。事实上若X＞X0时机器处于正常状态，但按式1所示的诊断规则，即当作异常状态报警。图1中曲线f（X/D1）下X＞X0的阴影面积表示发动机处于正常状态下的条件概率。式2。

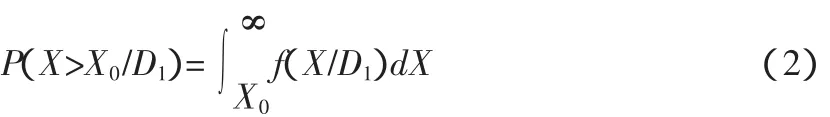
那么谎报的概率就应等于发动机处于正常状态的概率与在正常状态下X＞X0的概率的乘积，式3。

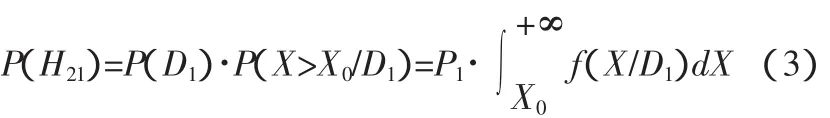
式中P1=P（D1）为状态D1的先验概率，可由积累的统计资料得到。同理，漏检的概率，式4。

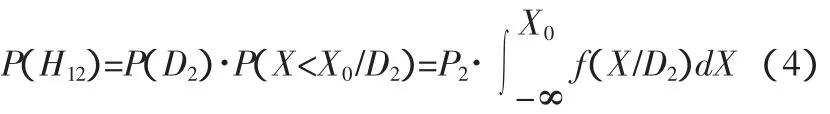
诊断错误的概率应是漏检的概率和谎报的概率之和。如果不仅考虑这2种错误诊断概率的大小，同时还考虑由于诊断错误所需要付出的代价，如漏检可能造成重大事故，其代价系数用“C12”表示；谎报则可能浪费人力物力，其代价系数用“C21”表示。一般情况下C12≥C21。这样即得到平均冒险率，式5。

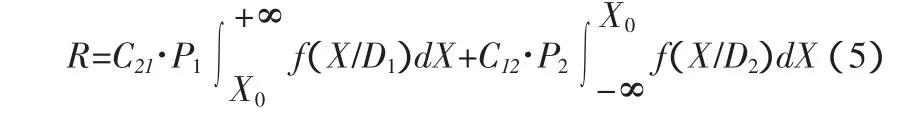
如同时考虑正确诊断（即H11，H22）所要付出的代价C11与C22，由于这种代价与错误诊断要付出的代价相比正好相反，所以应取负值。此时平均冒险率，式6。

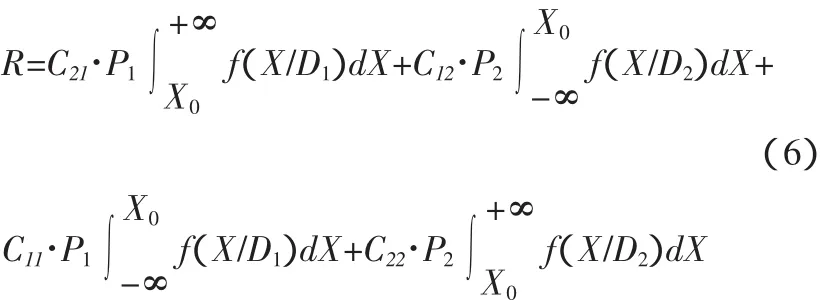
利用上式求解X0时，由于所提的要求不同，所以又有一些不同的求解方法。

2 故障分析及诊断决策模型建立

（1）最小冒险法。如果想使诊断的结果所冒的风险最小，也即满足平均冒险率组小的条件，即R＝Rmin。利用这种方法求出临界值X0的方法称为最小冒险法。

对式6在X0处求其导数，并令其导数为0，就可以确定X0的值。即：

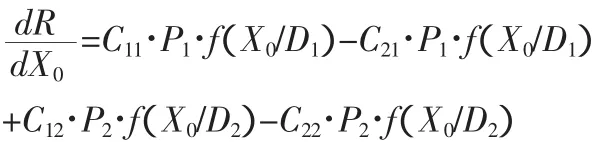
经整理得式7。

若由统计资料已知参数X在条件D1或D2下的分布密度，即可利用上式得到临界值X0。比如，设为正态分布，相应概率密度式8。

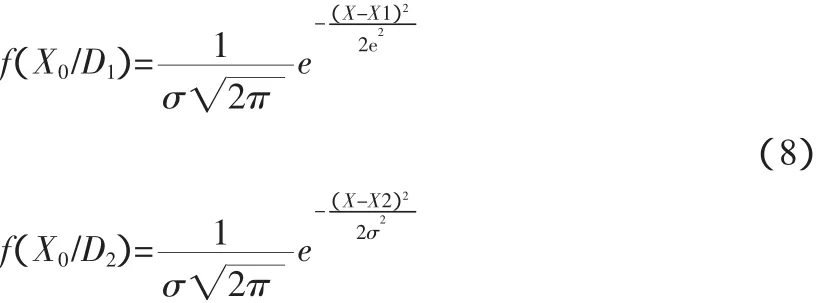
通过将以上2式代入以上整理过的公式中并取对数得

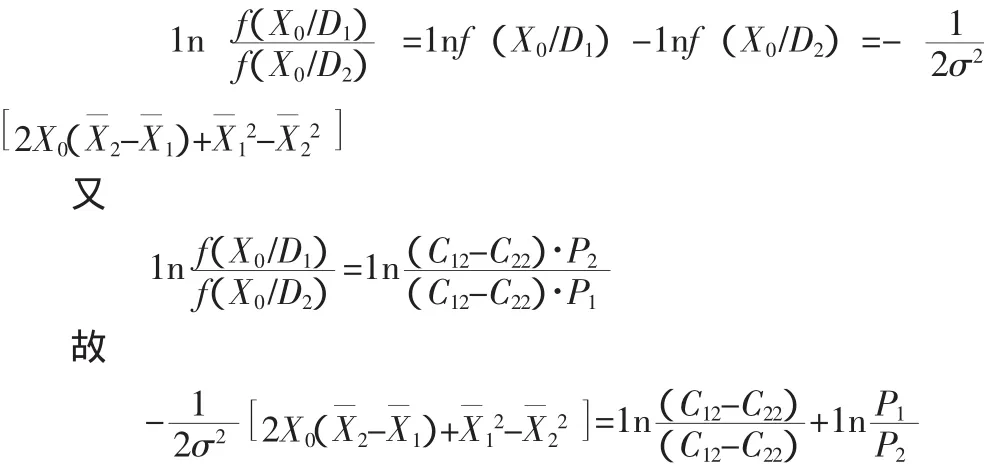
经整理后求得临界值式9。

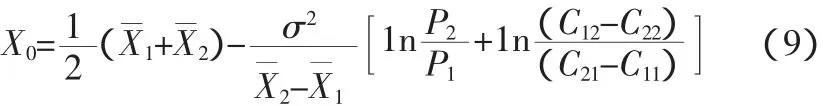
当X＜X0时，X∈D1，报为正常状态；当X＞X0时，X∈D2，报为异常状态。

（2）最小错误诊断概率方法。若不考虑错误诊断的代价，而且要求满足错误诊断的概率达到最小的条件下确定临界值X0，称为最小错误诊断概率方法。

由式3和式4可知，错误诊断的概率见式10。

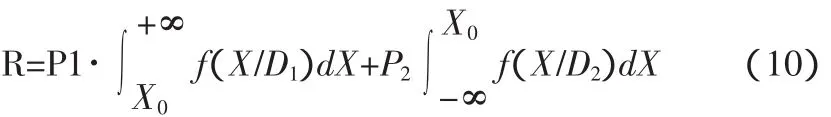
对R求X0处的导数，并令导数等于零，可得式11。

同上，若设X的条件分布仍为正态分布，可得式12。

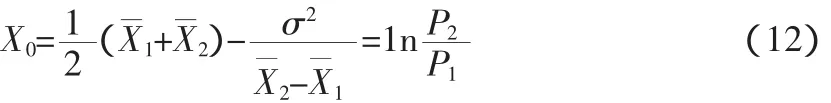
当X＜X0时，X∈D1，报为正常状态；当X＞X0时，X∈D2，报为异常状态。

最小错误概率条件只是最不冒险条件的一种特殊情况，式12所示选择临界值的条件，在学术术语中被称为“西克尔”条件。

3 在航空发动机滑油系统故障诊断的应用

海航某部在发动机定检过程中，根据油液分析室提取的滑油油液样品，测得滑油中的含铁量为6.84×10-6，按照正常情况为5×10-6，此时若按以往的排故经验判断，发动机的滑油系统此时应处于异常状态，则该批发动机应进厂排故，飞机则不能按时出动，这样直接影响日常的飞行训练，从某种程度而言，严重地降低了飞机的出动率，影响作战效能。然而经过专家论证，采用统计数值诊断法来对此批的发动机滑油系统进行故障分析时，依据上述2个诊断判别依据模型对系统进行分析如下：

根据滑油中含铁量监测发动机传动机匣的工作状态。设由统计资料（发动机履历本提供）得到：在正常状态下含铁量的均值X1=5×10-6mg/L，标准偏差σ1＝2；在异常状态下，含铁量的均值X2=12×10-6mg/L，σ2＝3；为正态分布，并已知发动机处于正常状态下的先验概率为：P1＝0.9；异常状态下P2=0.1。设漏检与谎报的代价比C12/C21＝20；C11＝C22＝0。下面分别用上述2种诊断决策规则求出滑油系统中含铁量的临界值X0。

首先采用决策规则中的第一种方法，即最小冒险法求出滑油系统中铁屑含量的临界值。

3.1 最小冒险方法

由式10可得：

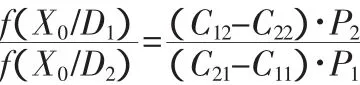
此处：

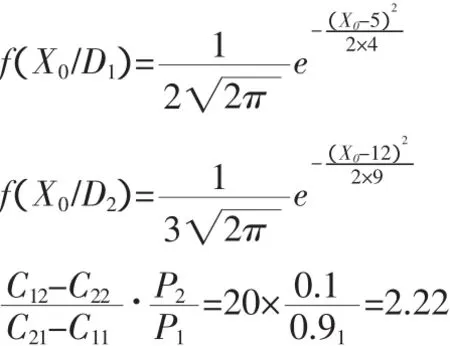
代入上式并在2边取对数可得：

得X0＝7.457与X0＝-8.65，负根明显不合理，故取正根X0＝7.457为含铁量的临界值。

下面采用决策规则中第2种方法，即最小错误诊断概率方法求出滑油系统中，铁屑含量的临界值。

3.2 最小错误诊断概率方法

由式6可得：

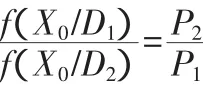
此处：

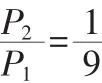
故得：

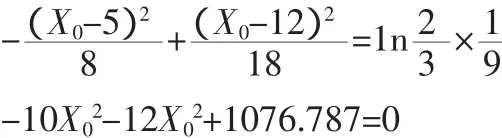
得正根X0＝9.794为含铁量的临界值。

即采用上述2种诊断依据模型对该批发动机的滑油系统分析判断时，均确认该批发动机的滑油系统此时不存在异常状态，飞机可以按照正常计划展开日后训练，经过日后长期的实践证明，上述诊断依据模型所确定的结论是正确的。不仅避免了部队人力、物力、财力的浪费，更保证了正常的训练，对提升我国海军航空兵的战斗力起到直接和重要的作用。

4 结束语

采用机械数值诊断方法中的统计数值诊断法，用来诊断判别某新型飞机的发动机滑油系统工作状态，用统计数学、概率论中的知识与外场发动机故障成因判定相结合。实践证明，该方法确定的发动机滑油系统工作状态正常与否的可靠性较高，而且大大缩短了发动机滑油系统故障诊断及排除的时间，也为计算机辅助故障诊断提供了一条可行的新途径。与此同时，在统计数值故障诊断过程中，由于发动机处于沿海环境中，腐蚀情况较为严重，另外其系统内部部件的磨损、老化，亦造成标准偏差存在一定的浮动性。所以模型中的一些参量还有待于进一步修改完善，以提高统计数值诊断模型的适应能力和准确性。

［1］孙红岩，姜雪峰.智能诊断中动态模糊征兆向量方法［J］.核动力工程，2010，（31）：67－70.

［2］Liu Xiao-feng，Ma Lin，Mathew J.Machinery Fault Diagnosis Based on Fuzzy Measure and Fuzzy Integral Data Fusion Techniques［J］. Mechanical Systems and Signal Processing，2009，23（3）：690－700.

［3］Li Li，Sun Yu-kuen，Li Yi-min.A new fuzzy fault diagnosis method［C］//Pro ceedings 5th Internatio nalCo nference on Fuzzy Systems and Knowledg e Discovery，FSKD 2008，l3：479-483.

［4］Su Q，Mi C，Lai L L，et al.A fuzzy dissolved Gas Analysis method for the diagnosis of multiple incipient faults in a transformer［J］.IEEE T ransaction on Power System，2000，15（2）：593-597.

［5］Liu Xiao-feng，Ma Lin，Mathew J.Machinery Fault Diagnosis Based on Fuzzy Measure and Fuzzy Integral Data Fusion Techniques［J］. Mechanical Systems and Signal Processing，2009，23（3）：690－700.

［6］孙红岩，姜雪峰.智能诊断中动态模糊征兆向量方法［J］.核动力工程，2010，（31）：67-70.

［7］王国彪，何正嘉，陈雪峰，等.机械故障诊断基础研究“何去何从”［J］.机械工程学报，2013，49（1）：63-72.

［8］尚文，王维民，齐鹏逸，等.基于条件规则与故障树法的燃气轮机故障诊断[J].机电工程，2013，07：798-801.

［9］胡兆勇.机械故障诊断中知识表达与推理的研究［D］.西安：西安交通大学，2005.

〔编辑 王永洲〕

V261

B

10.16621/j.cnki.issn1001-0599.2016.11.55