液压缸及辊缝控制下辊系非线性垂直振动分析

赵玉武，魏志恒

（1.河钢集团宣钢公司二钢轧厂，河北张家口075103；2.北京工业大学机电学院先进制造技术北京市重点实验室，北京100124）

液压缸及辊缝控制下辊系非线性垂直振动分析

赵玉武1，魏志恒2

（1.河钢集团宣钢公司二钢轧厂，河北张家口075103；2.北京工业大学机电学院先进制造技术北京市重点实验室，北京100124）

液压缸及辊缝处的非线性干扰是影响轧机辊系垂直振动的重要因素。对六辊轧机系统做适当简化并考虑轧机辊系垂直振动系统中的非线性刚度和非线性阻尼，建立了轧机垂直振动系统三自由度非线性动力学模型，求解得到相应的动力学微分方程。通过MATLAB软件进行仿真分析，得到轧机单自由度非线性垂直振动系统的时域振动曲线及主共振的幅频特性曲线。对时域振动曲线和幅频特性曲线分析，得到非线性因素下，轧机垂直振动的动力学特性。结果表明，辊系的垂直振动在非线性阻尼力作用下呈现较明显的摩擦阻尼特性，主共振的幅频特性在不同非线性刚度及非线性阻尼下表现各异。工程数据分析显示，液压缸及轧制界面的油液润滑状态，对轧机振动影响显著。

轧机；液压缸；辊缝；垂直振动；非线性

0 前言

轧机辊系的垂直振动是影响带钢质量的重要因素。辊系的垂直振动与轧机本身固有特性、轧制参数等有关，与此同时压下系统及轧制辊缝处的非线性因素也是影响辊系的垂直振动的重要因素［1-3］。A.Bar等建立了冷带轧机非线性参激扭振模型，模型考虑了轧制过程中存在的非线性参激振动现象并运用非线性方法分析得出了扭转响应的近似解；同时他还分析了含间隙的初轧机传动系统在打滑情况下轧机主传动系统振动的大小以及振动特征等问题，得出了与现场测试较一致的结果［4］。张瑞成等考虑轧机液压系统中液压缸与机架间的粘性阻尼及轧制界面非线性刚度，建立了轧机二自由度液压压下垂直振动系统模型。采用多尺度法求解了该模型在主参数共振情况下的一阶近似解，得到系统的频率响应方程，用数值方法研究了定常解的稳定性。分析了非线性刚度、液压缸的粘性阻尼等参数对系统振动的影响［5］。范小彬、臧勇等建立了含有Duffing振子和参激刚度项的板带轧机非线性振动动力学模型，选用立方函数形式的轧件迟滞模型，通过分析发现：轧辊振动在一定条件下会表现出分岔及混沌现象［6-7］。刘飞等研究了液压缸非线性约束下轧机辊系垂直振动行为发现轧机辊系振动速度受分段弹性力大小影响，系统不稳定频率区域随分段弹性力增大而变宽；摩擦力较小时，对辊系振动行为影响表现为阻尼特性，较大时，摩擦力的非线性成为影响辊系振动行为的主要特性［8］。目前对于轧机辊系非线性振动的研究主要集中在轧制辊缝、液压缸等含有油液润滑界面的部位，对于多非线性因素共同作用下轧机辊系振动行为特性尚未完全明了［9-14］。对六辊轧机系统做适当简化并考虑轧机辊系垂直振动系统中的非线性刚度和非线性阻尼，建立了轧机垂直振动系统二自由度非线性动力学模型，分析了不同参数下系统的时域幅频特性，为抑制辊系垂直振动提供了理论帮助。

1 轧机垂直振动系统动力学模型

1.1 轧机垂直振动系统三自由度非线性动力学模型

六辊轧机结构简图见图1，电机带动工作辊转动实现对轧件的轧制，工作辊与中间辊、中间辊与支承辊之间通过摩擦力实现传动。辊系在垂直方向上主要受到液压压下缸和轧制界面处轧制力的作用。液压压下缸作用在支承辊两端的轴承座上，主要作用是产生压下力。

机轧制过程中由于润滑油液的作用，在轧制界面会存在非线性刚度及非线性阻尼，同时液压缸液柱的存在，液压压下缸处也有非线性因素。由六辊轧机系统的结构及工作特性可知，辊系系统大致呈上下对称形态，此外在各辊缝中，轧制界面处存在的非线性因素最多，因此对六辊轧机辊系系统做适当简化得到三自由度非线性垂直振动动力学模型，见图2。

图1 六辊轧机结构简图

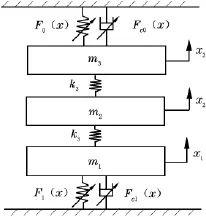
图2 辊系三自由度非线性垂直振动动力学模型

m1为工作辊的等效质量；m2为中间辊的等效质量；x1为工作辊垂直振动位移，x2为中间辊垂直振动位移，x3为支撑辊垂直振动位移，k2为中间辊和支撑辊之间的等效刚度，k3为工作辊和中间辊之间的等效刚度，F1（x）为轧制界面线性变形抗力，F0（x）为支承辊与液压压下系统之间的非线性弹性力，Fc1（x）为轧制界面非线性阻尼力，Fc0（x）为支承辊与液压压下系统之间的非线性阻尼力。由此可得轧机垂直振动系统三自由度非线性动力学方程，见式（1）。

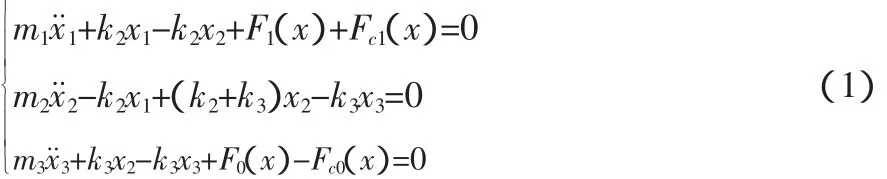
考虑到工程建模的实用性，动力学模型中的非线性项，采用在工程界得到广泛应用和认可的Vanderpol振子和Duffing振子的形式，即非线性刚度采用Duffing振子形式：（k0+k0′x2）x，非线性阻尼采用Vanderpo振子形式：（-c1+c1′x2）x˙［15］。其中为液压缸与支承辊间的线性弹性刚度系数，k0′为液压缸与支承辊间的非线性弹性刚度系数，c1制界面的线性阻尼系数，c1′为轧制界面的非线性阻尼系数。轧机轧制过程中三自由度非线性动力学方程的形式可转换为式（2）。

1.2 轧机垂直振动系统单自由度非线性动力学模型

由于只考虑轧制界面及液压压下系统的非线性因素影响，因此对系统进行求解时，可工作辊、中间辊及支承辊简化为单质量辊系系统，因此系统简化为单自由度，假设辊系受到的周期扰动力为Fcosωt。辊系单自由度垂直振动方程见式（3）。

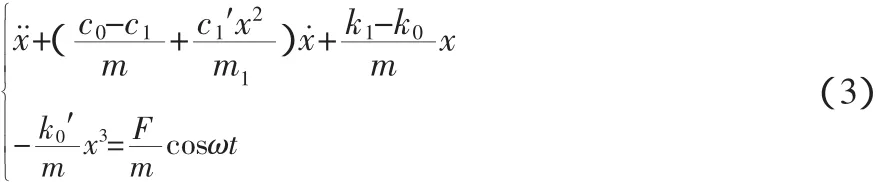
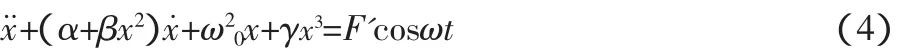
由式（4）可知系统垂直振动动特性，与非线性阻尼系数α，β以及非线性刚度系数γ有关。式（4）变形为式（5）。

整理可表示为式（6）。

当λ=1时，外部干扰的频率接近或等于系统的固有频率，此时，轧机垂振系统发生主共振。于是有式（8）。

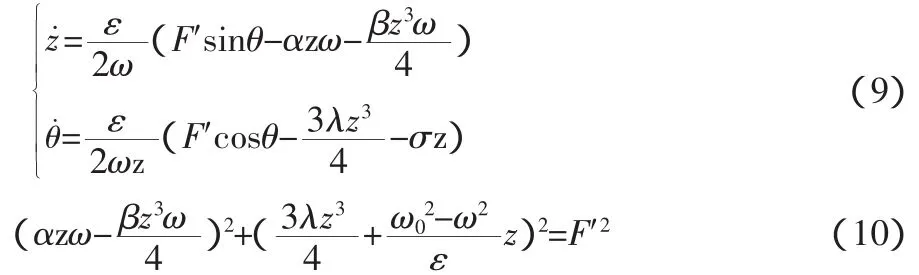
由（10）式可以看出，轧机垂直振动系统的振幅与频率主要和γ，β，α有关。

2 系统仿真分析

采用MATLAB软件，以某厂六辊轧机作为参数提取对象对垂直振动系统进行仿真分析。由式（7）可知轧机垂直振动系统二自由度非线性振动特性与各非线性参数有关，因此，可对不同参数下的动力学方程进行时域仿真求解。

2.1 时域特性分析

不同参数下辊系垂直振动曲线如图3～图5所示，图中可看出随着非线性阻尼系数的增大，辊系垂直振动波形在波峰及波谷处出现削尖现象。当非线性刚度系数的减小时，辊系垂直振动幅值有增大趋势。

图3 α=β=5，γ=10时的辊系垂直振动曲线

图4 α=10，β=10，γ=10，时的辊系垂直振动曲线

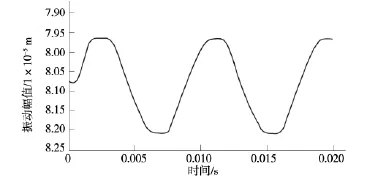
图5 α=β=10，γ=5时的辊系垂直振动曲线

2.2 频域特性分析

由式（4）可知轧机垂直振动系统的振幅与频率主要和γ，β，α有关。利用MATLAB软件对不同参数下系统的主共振幅频特性进行的仿真。

（1）不同刚度系数下轧机垂直振动系统主共振幅频特性的曲线

如图6所示曲线1，2，3分别是γ为-1，0.5，1时的主共振幅频特性曲线为曲线。随着非线性刚度系数的增大系统主共振幅频特性曲线的跳跃频率发生右移，说明系统刚到呀越大，激起系统共振的共振频率越高。

（2）不同阻尼系数下轧机垂直振动系统主共振幅频特性曲线

如图7和图8分别是不同阻尼系数下轧机垂直振动系统主共振幅频特性曲线。所示曲线1，2，3分别是α和β为-1，0.5，1时的主共振幅频特性曲线为曲线。由图7和图8可以看出，系统的幅频曲线的振幅最大值随着阻尼系数的增大而减小，不同阻尼下外部扰动跳跃频率的范围基本一致，不同的是随着非线性阻尼β的增大，轧机垂直振动系统的幅频曲线的振幅最大值减小。系统主共振振幅的跳跃大概发生在外部扰动频率ω=1.5时。

3 工程实践验证

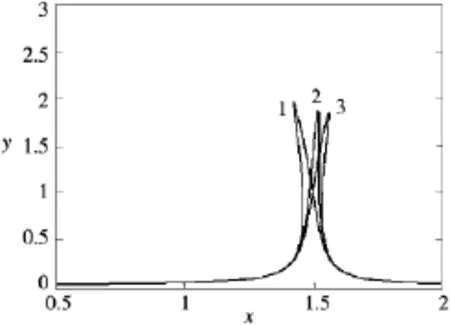
图6 不同非线性刚度γ对应的主共振幅频特性曲线

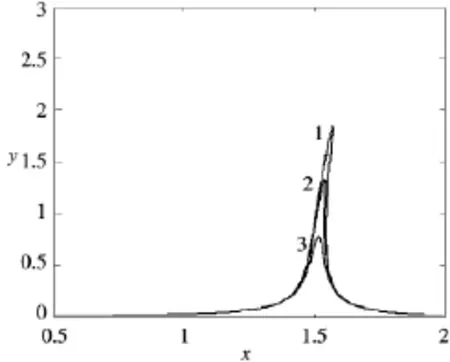
图7 不同阻尼系数α对应的主共振幅频特性曲线

图8 不同非线性阻尼β对应的主共振幅频特性曲线

对某钢厂六辊轧机F4台工作辊轴承座垂直方向进行长期振动监测。图9为液压缸油液更换早期轧制界面欠润滑状态下轧机工作辊轴承座垂直振动波形。图10为液压缸油液更换中期轧制界面适润滑状态下轧机工作辊轴承座垂直振动波形。图11为液压缸油液更换后期轧制界面过润滑状态下轧机工作辊轴承座垂直振动波形。油液黏度直接影响液压缸及轧制界面的动力学特性，由图10可得液压缸油液更换中期在轧制界面适当润滑情况下轧制振动值相对较小。由图9、图11可知，在初期和周期轧制振动相对较大，在液压缸油液更换早期及轧制界面欠润滑状态下由于油液状态不稳定性及轧制界面欠润滑状态导致阻尼增大，致使系统不稳定性增强。在后期由于设备长时间工作导致油液杂质增多，黏度变化导致液压缸及轧制界面处非线性刚度及阻尼发生变化，从而造成异常振动。

4 结论

考虑液压缸及辊缝处的非线性影响建立了轧机辊系垂直振动二自由度动力学模型，求解得到了相应的动力学微分方程。分析了不同参数下模型的时域特性及幅频特性。分析结果表明随着非线性阻尼的增大，辊系垂直振动波形在波峰及波谷处出现削尖现象。当非线性刚度系数的减小时，辊系垂直振动幅值有增大趋势。非线性刚度及非线性阻尼的大小对系统幅频特性影响较大，系统共振频率大小与非线性刚度成正比，系统振动幅值大小与非线性阻尼成反比。根据工程测试数据的分析可得液压缸油液状态及轧制界面的润滑状态直接影响其动力学特性，继而对轧机振动产生影响。因此可知实际工况下通过调整液压缸及轧制界面油液的润滑黏度继而改变其非线性特性，对调整系统共振的频带及抑制振动大小有一定帮助。

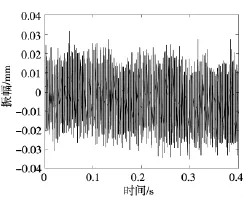
图9 早期振动波形图

图10 中期振动波形图

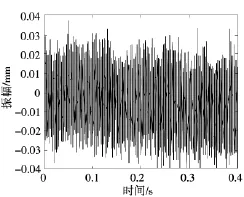
图11 后期振动波形图

［1］黄彬城，马维金，王俊元，等.高速轧机振动问题研究综述［J］.轧钢，2013，30（4）：38-42.

［2］闫晓强.连轧机振动控制重要进展综述［J］.冶金设备，2013，（2）：55-57．

［3］Sansal K Yildiz，Fraser Forbes J，Biao Huang．Dynamic Modelling andSimulationofaHotStripFinishingMill［J］．Applied Mathematical Modelling，2009，33（7）：3208．

［4］A.wi toniowski，A.Bar.Parameterical excitement vibration in tadem mills-mathematical model and its analysis［J］.Journal of Materials Processing Technolog，2003，134：224-224.

［5］张瑞成，马寅洲，高峥，等.轧机液压压下垂直系统非线性振动机理研究［J］.机械强度，2016，38（1）：006-011。

［6］侯东晓.轧机非线性振动建模及其动力学特性研究［D］.秦皇岛：燕山大学，2011.

［7］陈浩.轧机辊系非线性垂直振动特性研究［D］.秦皇岛：燕山大学，2009.

［8］刘飞，刘彬，时培明，等.液压缸非线性约束下轧机辊系垂直振动行为［J］.机械工程学报，2014，50（24）：20-25.

［9］刘浩然，刘飞，侯东晓，等.多非线性弹性约束下轧机辊系振动特性［J］.机械工程学报，2012，48（9）：89-94.

［10］B.Eugenio，L.Luca，Benasciutti.D.Vibration analysis of a Sendzimir cold rolling mill and bearing fault detection［J］.Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2010，224（8）：1645-1654.

［11］Jingcheng Wang，Chunzhao C.On the optimization of a rolling force model for a hot strip finishing line［J］.ISA Transactions，2007，46（4）：527-531.

［12］SUN Jianliang，PENG Yan，LIU H.Nonlinear Vibration and Stability of Moving Strip with Time-Dependent Tension in Rolling Process［J］.Journal of Iron and Steel Research（International），2010，17（06）：11-15.

［13］Eugenio Brusa，Luca L.Numerical and experimental analysis of the dynamic effects in compact cluster mills for cold rolling［J］. Journal of Materials Processing Technology，2009（5）：2436-2445.

［14］Guoyou LI，Min D.A wavelet and neural networks based on fault diagnosis for HAGC system of strip rolling mill［J］.Journal of Iron and Steel Research，2011，18（1）：31-35.

［15］高瑞进.四辊轧机垂直振动系统动力学建模及仿真分析［D］.杭州：杭州电子科技大学，2014.

〔编辑 利文〕

TH333

B

国家自然科学基金资助项目（51375019）

10.16621/j.cnki.issn.1001-0599.2016.11.35