基于格子Boltzmann方法的致密气藏微尺度效应研究
2016-12-20吴子森董平川袁忠超张雪娇曹耐杨书
吴子森,董平川,袁忠超,张雪娇,曹耐,杨书
(1.中国石油大学(北京)石油工程教育部重点实验室,北京 102249;2.中海油研究总院开发研究院,北京 100027)
基于格子Boltzmann方法的致密气藏微尺度效应研究
吴子森1,董平川1,袁忠超2,张雪娇1,曹耐1,杨书1
(1.中国石油大学(北京)石油工程教育部重点实验室,北京 102249;2.中海油研究总院开发研究院,北京 100027)
致密储层孔隙结构复杂,气体在致密孔喉中的流动存在微尺度效应,宏观流动规律难以准确描述其渗流特征。针对致密多孔介质孔隙主要分布在微纳米尺度的特点,建立修正克努森数(Kn)、固体边界处考虑镜面反弹(边界滑移效应)的格子Boltzmann模型。通过模拟压差驱动下的二维平板流动,验证了模型的正确性,并分析了克努森数对流动速度的影响。基于随机生长四参数生成法,对致密储层的二维微观孔隙结构进行了重构,利用修正格子Boltzmann模型进行流动模拟。结果表明:气体在致密储层中的流动存在微尺度效应,滑脱效应使得通道中间部分流体速度增大;在一定的压力梯度下,渗透率随着克努森数的增加而呈线性增加;克努森数不变时,渗透率随着平均压力倒数的增加而呈线性增加,即随着平均压力的增加,岩心的绝对渗透率减小。
致密砂岩;微尺度效应;格子Boltzmann方法;克努森数;渗透率
随着非常规油气资源日益受到重视,致密气藏的勘探开发逐渐成为热点[1-3]。由于致密储层岩性致密,渗透率极低,实验时对设备和技术人员要求较高,常规的实验方法难以保证实验数据的准确性和精度。作为一种介观模拟方法,格子Boltzmann方法可以对处理过的多孔介质图像进行流动仿真模拟[4-6],进而研究流体在多孔介质中的流动规律。基于格子Boltzmann方法,张云等[7-10]计算得到多孔介质渗透率,并与实验结果进行拟合,取得较好的效果。致密储层的孔径尺度从纳米级到微米级,存在多尺度效应。王勇杰等[11]研究指出,气体在致密多孔介质中流动时,存在明显的滑脱效应。气体分子与壁面或者其他分子发生碰撞,产生滑脱效应,使得气测渗透率大于多孔介质的绝对渗透率,因此,在研究致密气藏时,需要考虑孔隙的微尺度效应。前人在研究致密气藏中气体的微尺度效应时,多采用实验手段,数值模拟研究较少,且未考虑微尺度效应。笔者基于格子Boltzmann方法,采用随机生长四参数生成法,对储层的二维微观孔隙结构进行了重构,通过修正克努森数(Kn),考虑到气体的滑脱效应,模拟单相气体在致密储层中的流动,并分析了渗透率与克努森数、平均压力之间的关系。
1 格子Boltzmann模型
格子Boltzmann模型(LBM)一般由格子模型、平衡态分布函数和演化方程组成。基于该模型,笔者建立了致密气藏单相格子Boltzmann模型,模拟致密气藏的气相流动。模型计算过程由碰撞步和迁移步两部分组成,格子Boltzmann方程形式如下[12]:

Boltzmann方程中碰撞项采用单松弛时间形式:
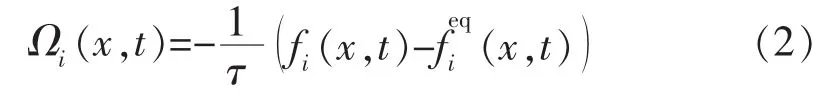
对D2Q9模型[11],平衡态分布函数可表示为
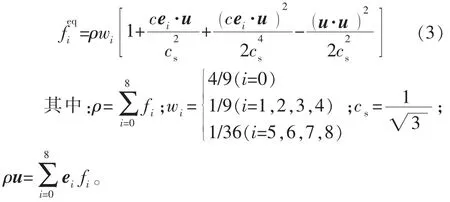
式中:fi(x,t)为t时刻x点处的密度分布函数;ei为离散速度向量,e0=(0,0),e1=(1,0),e2=(0,1),e3=(-1,0),e4=(0,-1),e5=(1,1),e6=(-1,1),e7=(-1,-1),e8=(1,-1);t为时间;Δt为时间步长;τ为松弛时间,与流体黏度有关;ρ为流体的宏观密度,g/cm3;wi为权系数;c为格子速度,一般取值为1;u为流体的宏观速度,m/s;cs为格子声速;下标i表示离散速度方向 (i= 0,1,…,8)。
1.1 松弛时间和边界处理
确定碰撞算子的τ,Kn以及微尺度流动中的边界处理,是格子Boltzmann方法模拟微尺度流动时需要解决的关键问题。宏观流动中,可用黏性系数确定τ;对于微尺度流动,特征参数是克努森数,在格子Boltzmann模型中,通过引入Kn,进而可修正τ。
对D2Q9模型,修正的松弛时间计算公式为[13-17]

边界滑移是微尺度流动的重要特征,采取有效准确的边界处理方法,才能正确地计算边界滑移速度,实现真实气体与固体之间的相互作用。本文采用将无滑移的反弹格式和镜面反弹按照一定比例组合而成的混合边界处理格式。
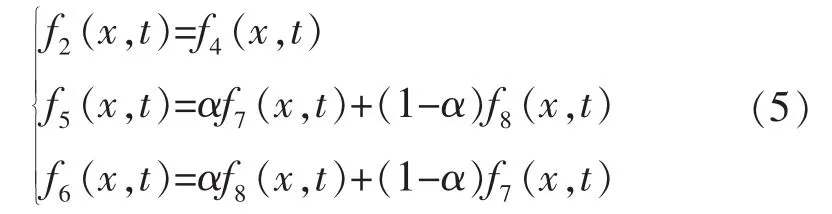
式中:α为标准反弹和镜面反弹的弹回比例系数。
α∈[0,1]。α=1时,表示标准反弹格式;α=0时,表示镜面反弹格式;α=0.5时,表示理想的漫反射。Tang等[16]研究发现,α=0.7时的计算结果与理论值吻合度较高。1.2 克努森数
在微尺度流动中,正确计算Kn是微尺度模拟流动的关键。

在实际中,Kn不仅与流动通道的特征尺寸有关,还与压力、温度有关。对于硬球分子:

式中:m为分子质量,g;R为气体常数,R=8.314 Pa·m3/(K·mol);T为温度,K;p为压力,Pa;M为分子摩尔质量,g/mol;d为分子直径,m。
将式(7)代入式(6),整理可得:

式中:NA为阿伏伽德罗常数(NA=6.022×1023mol-1)。
致密气的主要成分为甲烷,d约为0.414×10-9m,将给定温度和压力以及流动通道的特征尺寸带入式(8),即可算出Kn值。在T为350 K、H分别为10,20,50,100 nm时,计算得到Kn与p的关系(见图1)。计算得到Kn后,根据式(4)对τ进行修正,进而利用修正的格子Boltzmann模型模拟致密气流动。
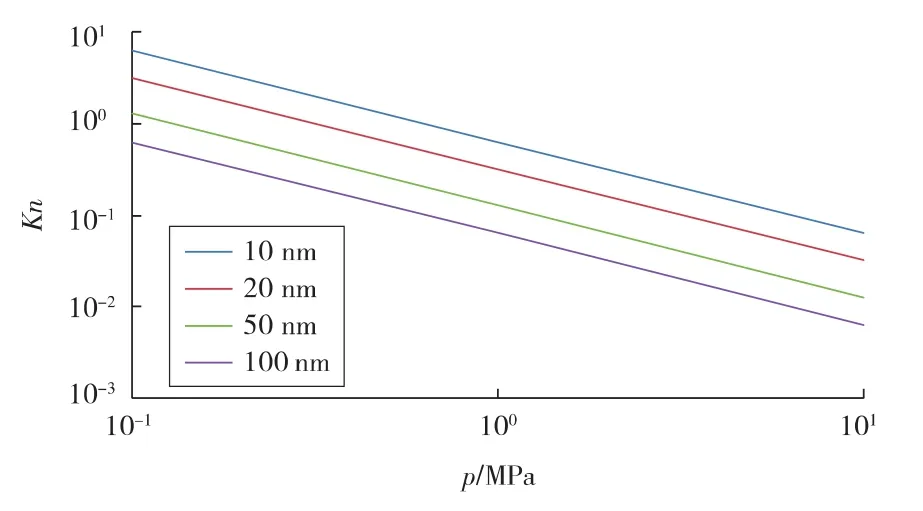
图1 Kn-p关系
2 格子Boltzmann模型验证
为了验证格子Boltzmann方法和模型的正确性,基于格子Boltzmann方法,模拟压力梯度驱动下二维平板间的泊肃叶流动,其渗透率理论值为l2/12(其中,l为两平板间的宽度,m)。
计算模型采用D2Q9模型,格子步长Δx=Δy=1;时间步长Δt=1;不考虑微尺度流动的影响,松弛时间τ= 1;出口边界和入口边界采用定压边界,上下固体边界采用标准反弹格式反弹处理。在x/l=0.5处截面上,无因次速度(u/umax)沿y方向的分布呈抛物线分布,可以看出模拟结果与解析解吻合较好(见图2)。

图2 x/l=0.5截面上的速度分布
微流动中,存在复杂的微尺度效应,因此利用格子Boltzmann方法研究微流动时,必须使用修正模型和正确的边界处理格式。图3为不同Kn对通道内流动的影响,流体流动方向由左往右,左右采用定压边界,上下采用反弹边界与镜面边界的混合边界格式,α=0.7。从图3可以看出,Kn对气体流速和边界滑移速度有很大的影响。
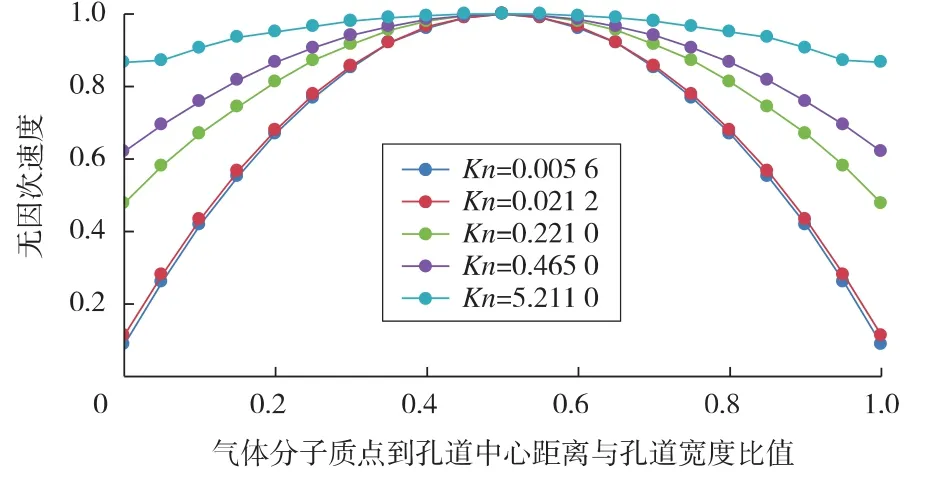
图3 不同Kn的无因次速度剖面
随着Kn的增加,壁面边界滑移速度逐渐增大,且通道流速剖面逐渐偏离抛物线分布的规律。当Kn<0.1时,此时流动区域处于滑移区,通道流速剖面呈抛物线型,壁面滑移速度增加幅度不大,这主要是因为当流动处于滑移区时,通道宽度远远大于分子平均自由程,此时分子间的碰撞占主导地位,流动以黏性流为主。当0.1<Kn≤10,随着Kn的增大,边界滑移速度增幅明显,主要是因为当流动区域处于过渡区时,分子与壁面间的碰撞所占比例逐渐增大,流动以努森流为主,边界滑移效应显著。
3 致密储层微尺度效应
由于致密储层孔隙结构复杂,连通性差,常规的电镜和CT扫描获得的岩心图像难以用于微观流动模拟。而通过数值重建方法,可以获取连通性较好的数字岩心[18-20]。目前数值重建方法主要有随机生长法和过程法。笔者基于Wang等[21]提出的随机生长四参数生成法(Quartet structure generation set,QSGS),重构致密储层微观孔喉结构,初始相全为孔隙,固体颗粒为生长相,构造的致密气藏数字岩心如图4a所示(黑色表示固体颗粒,白色表示孔隙颗粒)。
采用修正的格子Boltzmann模型,模拟单相气体在致密气藏中的流动。在模拟中,左端为入口,右端为出口,左右边界采用定压边界,入口压力p1=1.01 MPa,出口压力p2=1.00 MPa,上下采用混合边界格式,α= 0.7,Kn=0.050 0。图4b为气体在数字岩心中流动达到平衡状态时的速度分布。可以看出,气体流速在绝大部分连通孔隙中处于相对低速,只有在很少的孔隙中流速相对较高。

图4 致密气藏数字岩心
计算不同Kn和不同压力梯度下通过多孔介质的流体流量,然后带入达西公式,就可以计算出岩心的渗透率K[22]。K与Kn的关系如图5所示。从图5可以看出,在一定的压力梯度下,渗透率随着克努森数的增加而呈线性增加。这说明克努森数越大,气体分子的平均自由程越大,导致在相同压差下气体分子流动更快,气体滑脱效应越明显。
K与岩心进出口平均压力p¯之间的关系见图6(其中,p¯=(p1+p2)/2)。从图6可以看出,在相同的克努森数下,渗透率随着平均压力倒数的增加而呈线性增加,即随着平均压力的增加,岩心的绝对渗透率减小。这主要是因为平均压力越小,气体密度越小,气体分子间的碰撞就越少,气体滑脱效应越明显,渗透率越大。
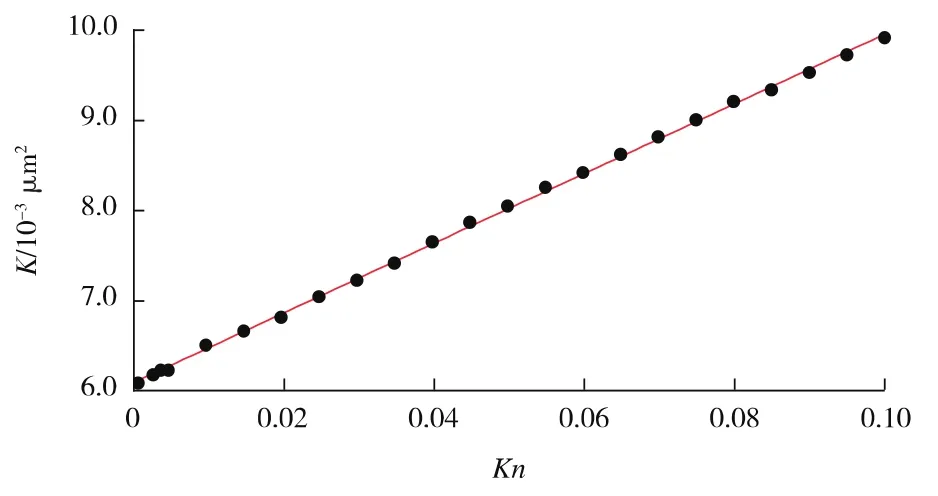
图5 一定压力梯度下K与Kn的关系(p1=1.01 MPa,p2=1.00 MPa)

图6 Kn不变时K与p¯的关系(Kn=0.050 0,p2=1.00 MPa)
4 结论
1)建立修正克努森数、固体边界处考虑镜面反弹(边界滑移效应)的格子Boltzmann模型,并验证了模型的正确性。
2)气体在纳米孔隙中的流动存在微尺度效应,滑脱效应使得通道中间部分流体速度增大。
3)在一定的压力梯度下,渗透率随着克努森数的增加而呈线性增加;克努森数不变时,渗透率随着平均压力倒数的增加而呈线性增加,即随着平均压力的增加,岩心的绝对渗透率减小。
4)利用修正的格子Boltzmann模拟模型,可便捷研究致密气藏微尺度,作为实验室物理实验方法的有效补充。
[1]赵崇镇.新场气田须五致密气藏缝网压裂技术[J].石油钻探技术,2015,43(6):70-75.
[2]赵超.致密气藏多段压裂水平井非稳态复合产能模型[J].断块油气田,2015,22(5):651-655.
[3]孙元伟,程远方,张矿生,等.考虑非达西效应的致密气藏裂缝参数优化设计[J].石油钻探技术,2014,42(6):87-91.
[4]王晨晨,姚军,杨永飞,等.基于格子玻尔兹曼方法的碳酸盐岩数字岩心渗流特征分析[J].中国石油大学学报(自然科学版),2012,36(6):95-98.
[5]刘学锋,孙建孟,王海涛,等.顺序指示模拟重建三维数字岩心的准确性评价[J].石油学报,2009,30(3):391-395.
[6]吴子森,董平川,雷刚,等.基于格子Boltzmann方法的油水两相流动规律[J].断块油气田,2016,23(3):338-341.
[7]张云.多孔介质中流动的格子Boltzmann模拟[D].北京:中国石油大学(北京),2011.
[8]张磊,姚军,孙海,等.利用格子Boltzmann方法计算页岩渗透率[J].中国石油大学学报(自然科学版),2014,38(1):87-91.
[9]宁正福,王波,杨峰,等.页岩储集层微观渗流的微尺度效应[J].石油勘探与开发,2014,41(4):445-452.
[10]ETREKIN T,KING G R,SCHWERER F C.Dynamic gas slip-page:a unique dual-mechanism approach to the flow of gas in tight formattions[J].SPE Formation Evaluation,1986,1(1):43-52.
[11]王勇杰,王昌杰,高家碧.低渗透多孔介质中气体滑脱行为研究[J].石油学报,1995,16(3):101-105.
[12]郭照立,郑楚光.格子Boltzmann方法的原理及应用[M].北京:科学出版社,2009:218-223.
[13]DONGARI N,AGRAWAL A.Analytical solution of gaseous slip flow inlong microchannels[J].International Journal of Heat and Mass Transfer,2007,50(17/18):3411-3421.
[14]LIM C Y,SHU C,NIU X D,et al.Application of lattice Boltzmann methodto simulate microchannel flows[J].Physics of Fluids,2002,14(7):2299-2308.
[15]ZHANG Y H,QIN R S,SUN Y H,et al.Gas flow in micro channels:a lattice Boltzmann method approach[J].Journal of Statistical Physics,2005,21(1/2):257-267.
[16]TANG G H,TAO W Q,HE Y L.Lattice Boltzmann method for simulating gas flow in microchannels[J].International Journal of Modern Physics C,2004,15(2):335-347.
[17]PERUMALDA,KRISHNAV,SARVESHG,etal.Numericalsimulation of gaseous microflows by lattice Boltzmann method[J].International Journal of Recent Trends in Engineering,2009,1(5):15-20.
[18]赵秀才.数字岩心及孔隙网络模型重构方法研究[D].青岛:中国石油大学(华东),2009.
[19]刘伟,张德峰,刘海河,等.数字岩心技术在致密砂岩储层含油饱和度评价中的应用[J].断块油气田,2013,20(5):593-596.
[20]李仁民,刘松玉,方磊,等.采用随机生长四参数生成法构造黏土微观结构[J].浙江大学学报(工学版),2010,44(10):1897-1901.
[21]WANG M,PAN N.Numerical analyses of effective dielectric constant of multiphase microporous media[J].Journal of Applied Physics,2007,101(11):114102.
[22]杨胜来,魏俊之.油层物理学[M].北京:石油工业出版社,2007:136-138.
(编辑 赵卫红)
Micro-scale effect in tight gas reservoir based on lattice Boltzmann method
WU Zisen1,DONG Pingchuan1,YUAN Zhongchao2,ZHANG Xuejiao1,CAO Nai1,YANG Shu1
(1.MOE Key Laboratory of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.CNOOC Research Institute,Beijing 100027,China)
The micro-pore structure of tight gas reservoir is complex,and gas flow in tight reservoir can lead to micro-scale effect which can′t be described by flowing law of macro fluid.Considering the micro-nano scale pores in tight sandstone,a lattice Boltzmann model(LBM)amended by Knudsen number has been established with a specular bounceback condition(slippage effect) on the solid boundary.The correctness of the new model is verified by the simulation of two parallel plates flow forced by differential pressure.The influence of Knudsen number on velocity was analyzed.With the multi-parameter random generation growth method (MRGGM),a 2D digital core of tight reservoir was reconstructured and the fluid flow behavior in this core was studied by the LBM. The results show that there exists micro-scale effect when gas flows in tight reservoir and the predicted flow velocity in the middle of the flat for the novel model will become larger because of the slippage effect.Under a certain pressure gradient,the permeability increases linearly with the increase of Knudsen number;when the Knudsen number is constant,the permeability increases linearly with the reciprocal of the average pressure,which means the absolute permeability of core decreases with the increase of average pressure.
tight sandstone;micro-scale effect;lattice Boltzmann method;Knudsen number;permeability
国家自然科学基金项目“基于孔隙网络模型的多孔介质近混相油气水三相流动模拟研究”(11072268)
TE311
A
10.6056/dkyqt201606022
2016-04-14;改回日期:2016-08-26。
吴子森,男,1984年生,在读博士研究生,从事油气田开发工程研究工作。E-mail:wuzisen@163.com。
吴子森,董平川,袁忠超,等.基于格子Boltzmann方法的致密气藏微尺度效应研究[J].断块油气田,2016,23(6):793-796.
WU Zisen,DONG Pingchuan,YUAN Zhongchao,et al.Micro-scale effect in tight gas reservoir based on lattice Boltzmann method[J]. Fault-Block Oil&Gas Field,2016,23(6):793-796.
