基于PM2.5指标的中国环境库兹涅茨曲线估计

李龚

（上海交通大学 安泰经济与管理学院，上海 200030）

基于PM2.5指标的中国环境库兹涅茨曲线估计

李龚

（上海交通大学 安泰经济与管理学院，上海 200030）

文章利用2014年中国138个城市截面数据与空间计量经济学模型，基于扩展的传统环境库兹涅茨曲(EKC)，以PM2.5为环境指标，分析我国城市环境污染的空间相关性、EKC的形状及其影响因素。结果发现：我国城市环境污染存在明显的空间正相关性，截面数据模拟出的EKC曲线呈现“倒U形”，EKC假说在我国城市尺度得到证实；第二产业比重、人口密度、汽车保有量等与环境污染呈现正相关；城市产业结构升级，统筹区域发展，控制城市汽车保有量以及多城市联合治理，有利于环境质量的提高。

环境库兹涅茨曲线；PM2.5；空间计量经济学模型；产业结构

0 引言

20世纪90年代初期，美国经济学家Grossman和Krueger提出环境库兹涅茨曲线(Environmental Kuznets Curve,EKC)，表明经济增长与环境污染之间呈现“倒U形”关系，即环境质量会随着经济的增长呈现先恶化后改善的趋势[1]。我国关于EKC的研究始于1999年，主要研究则在2002年以后。随着经济的不断发展，社会对环境的关注日益增加，以及最近几年“低碳经济”的概念日益深入人心，环境问题也随之成为经济学研究的热点。李慧明等(2003)研究发现，我国目前的环境质量仍然处在“局部改善，整体恶化”的状态，并且还没有达到EKC的转折点，更加不可能达到EKC曲线的右侧[2]。林伯强等（2009）以二氧化碳的排放量作为环境的代理指标，选取了1960年至2007年的中国二氧化碳排放量数据，使用了人均收入作为解释变量的二次方程，估算出了我国EKC呈现“倒U形”关系，并且从理论上估计了我国EKC曲线的拐点是人均GDP37170元[3]。杨万平等（2009）以1982年至2006年我国6大类工业环境污染数据为基础，使用改进的熵值法估算我国的EKC曲线，其结果表明：我国经济增长和环境污染之间不存在“倒U形”关系，而是呈现“正U形”关系[4]。苏梽芳等(2009)利用中国28个省域2003年至2005年的面板数据，使用空间面板数据模型对EKC进行了估计，其结果表明：区域污染存在空间相关性，区域污染排放不仅受本区域人均收入影响，且相邻区域的污染物排放也对本区域有重大影响，污染物排放具有空间溢出作用[5]。罗岚等（2012）利用了2000年至2009年我国各省份的面板数据，以废水、废气和固体废弃物为环境指标，估算了各个指标下的EKC，其结果表明：以三废作为环境指标估算出的EKC在大部分省均呈现“倒U形”；废水污染在未来十年内可以实现与经济发展同时改善，而固体废弃物和废气则要相对较迟[6]。高宏霞等（2012）搜集了2000年至2009年31个省市自治区的面板数据，对全国31个省市自治区进行了研究，结果表明我国各省份的EKC呈现“倒U形”，并且大部分省份的EKC拐点是在2020年以后[7]。吴玉鸣等（2012）扩展了传统的EKC模型，引入了城市化率，引进了人口数、人力资本、产业结构及对外开放等因素，利用2008年我国31个省份的截面数据，使用空间计量经济学模型，分析了我国EKC的形状及其影响因素，以及省域环境污染的空间相关性，其结果表明：我国省域环境污染之间存在明显的空间自相关性；同时，30个省域的EKC呈现倒U型[8]。

本文所选取的环境指标是PM2.5浓度。PM2.5指的是大气中粒子直径小于或等于2.5微米的颗粒物，又称细颗粒物。PM2.5有直径小、表面积大、活性强、容易携带有毒有害物质、在大气中停留时间长、输送距离远等特点，对人体健康影响较大。PM2.5的来源分为两种，分别是自然源与人为源，其中主要来自人为源，包括道路扬尘、工业粉尘、化石燃料的燃烧等[9]。PM2.5的上述特征表明，PM2.5不是单一的污染物，而是一种综合性环境污染指标。

综上可知，学者们在研究EKC曲线的时候，大多只用人均GDP或人均收入这一个指标作为解释变量，而忽略了其他指标的影响，比如产业结构、人口密度等，同时也忽略了区域环境污染之间的空间自相关性。选取的环境指标通常都是“三废”、粉尘、二氧化硫、二氧化碳等，这些都是单一的环境指标而不是综合的环境指标。文献中得到的EKC形状各异，有“倒U形”[10]、“正U形”[4,12]、“N形”[11]、“N形+倒U形”[13]、“凹形”[14]等。

与以往EKC的研究相比，本文有如下的三点不同：第一，本文利用了PM2.5浓度作为环境污染的指标。在国内的EKC研究中，尚且没有选择PM2.5浓度为环境指标；同时PM2.5本身是一种综合的环境指标，与之前的EKC研究中使用的单一指标不同。第二，本文搜集了2014年我国138个城市的相关截面数据。目前，在相关EKC研究中，大多是基于国家或者省市自治区层面，很少有城市层面的EKC研究。第三，基于PM2.5易扩散的物理特征，本文采用了空间计量经济学模型，从而控制相邻地区PM2.5的相关性。

1 研究模型、方法和数据

1.1 空间自相关[15]

空间自相关指的是某个变量在同一分布区域里的观察值之间存在潜在的相互依赖关系。全局区域自相关是从区域整体上刻画空间聚集情况。通常用全局莫兰指数(Moran’s I)来度量全局空间自相关，其计算公式如下：

在衡量某一特定区域附近的空间聚集情况的时候，通常选用局部莫兰指数(Local Moran’s I)，其公式如下：

其中yi和yj分别是第i和第j个地区的观察值，n是地区总数量，表示所选指标的均值，s2是所选指标的方差，ωij是空间权重的值。

全局莫兰指数的取值范围在-1到1之间，大于0则存在正相关关系，小于0则存在负相关关系，等于0则不存在空间关系，绝对值越大则表示相关关系越强。正的局部莫兰指数表示该区域的高值被周围的高值所包围，或者该地区的低值被周围的低值所包围；反之则表示该区域的高值被周围的低值所包围，或该区域的低值被周围的高值所包围。

1.2 空间计量经济学模型

空间计量经济学模型可以分为空间滞后模型(Spatial Lag Model,SLM)和空间误差模型(Spatial Error Model, SEM)。

(1)空间滞后模型(SLM)[16]

在模型中考虑因变量的空间滞后项，则可以选择空间滞后模型：

其中，yi是因变量；ω是n×n阶的空间权重矩阵；∑i≠jωijyi是所有邻近区域地区因变量的加权和，作为因变量的空间滞后项，ρ是衡量因变量溢出效应的参数，称为空间自回归系数；xi是n×k的自变量矩阵，β是参数，反映自变量对因变量的影响程度；εi是随机误差项。

(2)空间误差模型(SEM)[17]

当因变量的空间依赖性存在于随机扰动项的时候，则可以考虑使用空间误差模型：

其中，μi是随机误差项；λ是μi的自回归系数，用来衡量邻近地区因变量yi的误差项加权总和∑i≠jωijμi对因变量yi误差项的影响程度；εi是正太分布的随机误差项。

1.3 选取指标

本文所涉及的指标如下：

(1)PM2.5浓度：作为实证分析中环境质量的代理指标，它与环境质量呈现负相关关系，即环境质量得到改善则PM2.5浓度下降，反之PM2.5浓度上升。

(2)人均GDP：根据环境库茨涅兹曲线的理论，经济的发展与环境污染之间呈现“倒U形”关系，即在经济发展初期，社会以牺牲环境质量为代价来换取人均GDP的提高，环境质量开始逐步恶化，然而，当人均GDP到达一定程度之后，社会开始逐步关注环境质量，于是伴随着人均GDP的逐步提高，环境质量也在不断提高。

(3)汽车保有量：汽车尾气是PM2.5的主要来源之一。本文为了研究PM2.5浓度与人均GDP的关系，需要控制住其他影响PM2.5浓度的变量，而城市的汽车保有量是一个影响PM2.5浓度的重要因素。本文假设城市的汽车保有量与城市的PM2.5呈现正相关关系，即城市的汽车保有量增加会导致PM2.5的浓度也相应地增加。

(4)总降水量：雨水会溶解大气中的有害颗粒物，从而达到清洁大气的作用。本文假设PM2.5浓度与降水量呈现负相关关系，即降水量越大则对应的PM2.5浓度就会越低，反之，PM2.5浓度将会越高。

(5)第二产业比重：在第一、第二和第三产业中，第一和第三两个产业是相对比较清洁的，不会对环境造成过多的影响，而第二产业则是影响环境质量的重要来源。本文假设第二产业的比重与PM2.5浓度呈现正相关关系，即第二产业的比重越大，则PM2.5浓度就会越高，反之PM2.5浓度就会越低。

(6)人口密度：人口密度越高则对环境的压力就会越大，造成的环境污染就可能更加严重。本文假设人口密度与PM2.5之间呈现正相关关系，即人口密度越高，对应的PM2.5浓度就会越高，反之PM2.5浓度就会越低。

(7)是否在秦岭淮河以北：这个指标作了哑变量处理，处于秦岭淮河以北的城市取1，否则取0。秦岭淮河线从地理上将我国分成了南北双方，同时也是人文上的分割线，是我国所特有的。我国800毫米等降水线于秦岭淮河一线重合，越向北降水量越少；我国在秋冬两季实行集体供暖，而供暖城市绝大多数都是位于秦岭淮河以北，供暖会消耗大量能源，同时会产生大量的环境污染。本文假设该哑变量与PM2.5浓度呈现正相关关系，即在同等情况下，秦岭淮河以北的PM2.5浓度会高于秦岭淮河以南。

1.4 数据说明与实证模型构建

本文所涉及到的数据源于我国2014年138个城市，包括：PM2.5浓度(PM25，单位：微克/立方米)、降水量(RAIN-FALL，单位：毫米)、汽车保有量(CARNUM，单位：万辆)、人均GDP(单位：元)、第二产业比重(INDUSTRY)、人口密度(POPDENSITY，单位：万人/平方公里)以及是否秦岭淮河以北(ISNORTH)。其中，2014年138个城市的PM2.5浓度数据和降水量数据来自于新浪网；汽车保有量、人均GDP和第二产业比重来自于2014年各城市国民经济与社会发展统计公告；人口密度是根据各个城市人口数量和面积计算得到。

本文是以PM2.5浓度作为环境指标，控制影响PM2.5浓度的其他的变量，即汽车保有量、总降水量、第二产业比重、人口密度、是否秦岭淮河以北，来估计人均GDP与环境质量的关系，从而得出环境库茨涅茨曲线的形状。本文选用的是基于截面数据建立的静态空间计量模型，将PM25、AVGGDP、CARNUM、RAINFALL和POPDENSITY这几个变量进行对数化处理，根据模型(3)和模型(4)分别建立如下的两个空间计量模型，即空间滞后模型(SLM)和空间误差模型(SEM)：

空间滞后模型(SLM)：

空间误差模型(SEM)：

2 实证结果分析

2.1 空间相关性的检验

首先，基于城市空间实际距离生成空间权重矩阵，然后对138个城市的对应变量数据进行全局空间自相关检验，其结果表1所示，其中I表示全局莫兰指数，E(I)表示其理论期望，SD(I)表示其理论标准差，Z表示其标准化值。

表1 EKC变量的全局空间自相关检验

根据距离空间权重计算PM2.5，降水量、人口密度、人均GDP以及是否是秦岭淮河以北的全局莫兰指数分别是0.478，0.336，0.206，0.349，0.791，都通过了1%的显著性检验水平，说明这些变量在空间分布上都存在明显的正自相关。而第二产业比重与汽车保有量相对而言就不存在明显的空间自相关性。综合以上结果，在研究城市EKC问题的时候不能忽视城市之间的空间效应。

2.2 空间计量估计与分析

为了与城市截面的EKC空间计量结果进行比较，本文首先用常规的普通最小二乘法(OLS)进行回归估计，然后使用Stata进行SLM和SEM两个模型的估计，并得到结果，见表2。

表2 OLS、SLM和SEM估计结果

OLS的估计结果表明：OLS的拟合优度是0.3569，F值是10.29，模型整体上通过了1%显著性检验。人均GDP、人均GDP的平方、是否秦岭淮河以北，通过了5%的显著性检验；人口密度和第二产业比重通过了1%的显著性检验；而汽车保有量和降水量则没有通过12%的显著性检验，即不显著。前面的全局莫兰指数检验表明城市之间的因变量存在明显的空间相关性，OLS的结果与之不符，表明OLS模型的设定存在问题，即OLS可能忽略了城市之间的空间相关性。

从SLM和SEM的估计结果可以看出：SLM中人均GDP、人均GDP的平方、汽车保有量、人口密度、第二产业比重以及是否秦岭淮河以北，这几个变量都通过了5%的显著性检验；而降水量通过了10%的显著性检验；空间自相关系数通过Wald Test、LRTest以及LM Test，显著性都在1%。SEM中人均GDP、人均GDP的平方、汽车保有量、人口密度、第二产业比重以及是否秦岭淮河以北，这几个变量也都通过了5%的显著性水平检验；而降水量通过了10%的显著性检验；空间自相关系数通过LRTest和LM Test的检验，显著性在1%，而在Wald Test中，没有通过10%的显著性检验；SLM和SEM的拟合优度R2分别是0.5580603和0.4920067，明显大于OLS的0.3569。

根据模型的估计结果，得出SLM的方程，即EKC模型是：

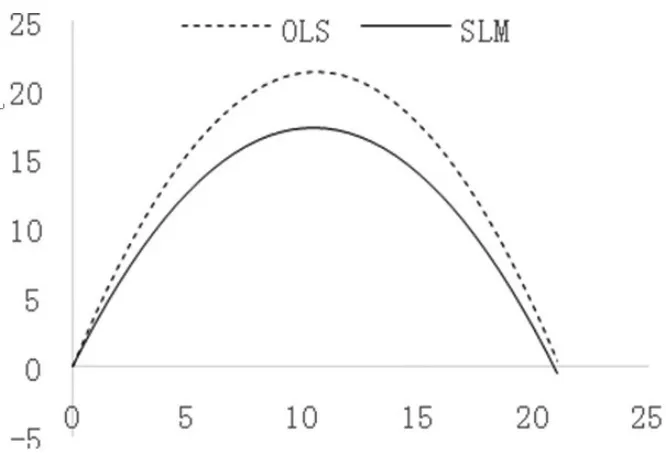
图12014 年中国138个城市截面

对于人均GDP而言，OLS和SLM模型的走势如图1。可以看出，OLC和SLM估算出的EKC都呈现“倒U形”，且两条曲线的拐点相近。同时在SLM估算出的ELC中，当lnAVGGDP达到10.4198219的时候达到拐点，即人均GDP达到33517.5元时，EKC达到拐点。根据数据可以知道，我国138个城市中绝大部分城市的人均GDP都超过了上述拐点，只有29个城市没有超过拐点。即这些城市目前仍是以牺牲环境质量为代价来发展经济。从图上看，SLM的曲线比数据EKC图OLS的曲线平缓，因为OLS没有考虑到空间的自相关效应，把周边地区溢出的污染也算进本地区的污染中，使得PM2.5浓度对人均GDP的变化更加敏感，说明了在忽略空间自相关效应的OLS中，夸大了人均GDP对PM2.5浓度的影响，从而可能会导致在环境治理上过度关注人均GDP的变化而忽略其他因素。

2.3 SLM的结果分析

汽车保有量（lnCARNUM）对环境污染的回归系数是0.0720433，通过5%的显著性水平检验，表明在不考虑其他因素的情况下，汽车保有量每增加1%，环境损失将增加0.0720433%。较大规模的汽车保有量对环境保护造成了较大的压力。一线大中型城市目前已经对城市的汽车数量进行一定的限制，这些措施也进一步表明了较大的汽车保有量对环境质量确实造成了不小的压力。

人口密度（lnPOPDENSITY）对环境污染的回归系数是1.050023，通过了5%的显著性水平检验，表明人口密度每增加1%，环境损失将增加1.050023%。京津冀的环境污染相对比较严重，这与当地较高的人口密度也不无关系。这就表明了要改善大中型城市的环境就有必要合理化分配城市配套资源，减小区域发展之间的不平衡。

降水量（lnRAINFALL）和是否秦岭淮河以北（ISNORTH）这两个因素对环境污染的回归系数分别是-0.1028827和0.1309262，分别通过了10%和5%的显著性检验。降水量反映了各个城市之间的气候差异。降水较多的南方会冲洗掉环境中的一些杂质，这样有利于环境的自我净化和修复，即在其他因素不变的情况下，降水量越多，环境质量越好。这与模型回归的结果是相同的。是否处与秦岭淮河以北从地理的角度讲我国分成了南方和北方。北方城市在冬季会采取集中供暖，而南方城市则没有。北方城市冬季采取集中供暖必然会给环境造成损失，这与模型的回归结果也是一致的。

第二产业比重（INDUSTRY）对环境的回归系数是0.8276416，通过了1%的显著性水平检验，表明了第二产业比重每增加1%，环境损失就会增加0.8276416%。第二产业主要以制造业为主，需要消耗大量的自然资源，同时也会对环境造成不可避免的伤害。模型的系数中第二产业比重的回归系数是最大的，说明了在模型列举的因素中，第二产业比重是对环境影响最大的。这进一步表明了产业结构调整对环境保护的重要性。

与SLM估计结果比较，OLS中人口密度、是否秦岭淮河以北这两个变量的系数偏大，原因是OLS模型中把其他周边区域的影响也算成本地区的影响，故而OLS的结果会偏大；第二产业比重、降水量的系数与OLS模型的结果相比，几乎没有变化；OLS模型中汽车保有量的系数比SLM中的系数偏小，说明汽车保有量的影响在OLS中被低估了，同时在OLS中该变量没有通过显著性检验，即OLS不能有效说明汽车保有量的影响。

3 结论

本文扩展了传统的环境库茨涅茨曲线模型，添加了汽车保有量、人口密度、降水量、第二产业比重、是否秦岭淮河以北这5个变量，利用空间计量经济学模型，研究了我国138个城市的EKC的形状及其影响因素。结果发现：我国PM2.5浓度在空间分布上存在明显的正自相关关系，说明我国各个城市环境污染不是相互独立的，而是存在空间正向自相关的；利用2014年度我国138个城市的相关截面数据模拟得出的EKC图形是呈现“倒U形”，表明EKC假说在我国可以得到历史数据的支持；同时估计出扩展后的EKC对人均GDP的拐点是33517.5元，即在其他因素不变的情况下，人均GDP达到或超过33517.5元的城市的环境质量会随着经济的发展而逐步改善。

基于上述的结果获得的政策建议如下：由于环境污染是存在空间相关性的，所以城市在治理环境的时候，要注重城市区域之间的合作；城市的产业结构要不断调整，要逐步改善第一、第二和第三产业的比重，积极发展第三产业，使产业逐步升级；大中型城市要合理控制汽车保有量，提升城市交通和环境质量；在推进城市化的过程中，要逐步实现城市之间基础设施及相关服务的均衡，避免人口过度集中。

[1]Grossman G M,Krueger A B.Economic Growth and The Environment [J].Quarterly Journal of Economics,1995,110(2).

[2]李慧明,卜欣欣.环境与经济如何双赢——环境库兹涅茨曲线引发的思考[J].南开学报（哲学社会科学版）,2003，(1).

[3]林伯强,蒋竺均.中国二氧化碳的环境库兹涅茨曲线预测及影响因素分析[J].管理世界,2009，(4).

[4]杨万平,袁晓玲.环境库兹涅茨曲线假说在中国的经验研究[J].长江流域资源与环境,2009,18(8).

[5]苏梽芳,胡日东,林三强.环境质量与经济增长库兹尼茨关系空间计量分析[J].地理研究,2009，(2).

[6]罗岚,邓玲.我国各省环境库兹涅茨曲线地区分布研究[J].统计与决策,2012，(10).

[7]高宏霞,杨林,付海东.中国各省经济增长与环境污染关系的研究与预测——基于环境库兹涅茨曲线的实证分析[J].经济学动态, 2012，(1).

[8]吴玉鸣,田斌.省域环境库兹涅茨曲线的扩展及其决定因素[J].地理研究,2012,31(4).

[9]王玮,汤大钢,刘红杰.中国PM2.5污染状况和污染特征的研究[J].环境科学研究,2000,13(1).

[10]高静.中国SO2与CO2排放路径与环境治理研究:基于30个省市环境库兹涅茨曲线面板数据分析[J].现代财经,2012，(8).

[11]丁继红,年艳.经济增长与环境污染关系剖析:以江苏省为例[J].南开经济研究,2010,(2).

[12]李忆雯,王君,周丽蓉.四川经济增长与环境污染关系的实证研究[J].统计与决策,2012，(13).

[13]苏营营,余建林,蒲凤莲等.嘉兴市环境库兹涅茨曲线特征分析[J].环境科学与管理,2012,37(2).

[14]班春峰,徐梦洁,赵紫玉等.河南省环境库兹涅茨曲线的实证研究[J].环境科学与管理,2008,33(9).

[15]Anselin L.Local Indicators of Spatial Autocorelation—LISA[J].Geo⁃graphical Analysis,1995,27(2).

[16]Ord K.Estimation Methods For Models of Spatial Interaction[J].Jour⁃nal of the American Statistical Association,1975,70(349).

[17]Anselin L.Spatial Econometrics:Methods and Models[J].Journal of the American Statistical Association,1990,85(411).

（责任编辑易永生）

X820

A

1002-6487（2016）23-0021-04

李 龚（1992—），男，江苏盐城人，硕士研究生，研究方向：产生经济学。