一种基于证据间距离和信息熵的证据组合方法∗

金晓斌，许大琴，谈 亮

（海军指挥学院，江苏南京 211800）

一种基于证据间距离和信息熵的证据组合方法∗

金晓斌，许大琴，谈 亮

（海军指挥学院，江苏南京 211800）

针对改进的基于证据间距离的组合方法，首先计算证据间距离并求出各个证据的支持度和可信度，选取支持度高的作为较可信证据，其次引入证据信息熵，计算修正系数，对这些证据的可信度进行修正，将可信度作为权重，进行证据的加权平均，再利用Dempster组合规则对所有证据进行融合。算例表明，该方法比现有的方法更加有效。

证据理论；冲突证据；证据距离；信息熵

D⁃S证据理论算法结构简单、融合精度高，能较好地对不确定信息进行处理，已经成为一种重要的决策融合方法［1⁃3］，在信息融合尤其是目标识别领域有着广泛的应用。在实际军用信息融合系统中，由于来自自然或者人为的干扰，会使一些传感器输出与实际情况不符的信息，导致收集的证据存在冲突。但D⁃S证据理论在处理冲突证据时，有时会产生有悖常理的结果。为了解决这个问题，国内外学者提出了各种各样的解决方法［4⁃12］，但这些方法在某种程度上都存在一些问题。本文在现有方法的基础上，提出一种改进的加权证据组合方法，并通过实例与现有几种方法进行比较，结果表明本文方法在融合时效果更好。

1 经典D⁃S证据理论

假设Θ为问题θ所有的可能目标的集合，即Θ＝｛θ1，θ2，…θn｝，Θ内的元素有限可穷举并且互不相容，则称Θ为θ的识别框架。

1.1 基本信任分配函数和信任函数

定义1 设Θ为一识别框架，若函数m：2Θ→［0，1］满足以下条件：

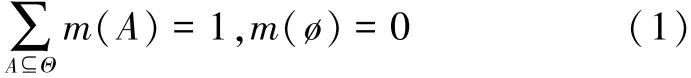
则称m（A）为A基本信任（概率）分配函数BPA。

定义2 设识别框架Θ上的函数Bel：2Θ→［0，1］，满足以下条件：

则称Bel为信任函数，表示A对应命题被相信为真的程度。

1.2 组合规则

定义3 设两个证据E1和E2属于同一识别框架Θ，对应基本信任函数为m1和m2，焦元是Aj、Bj，D⁃S组合规则为

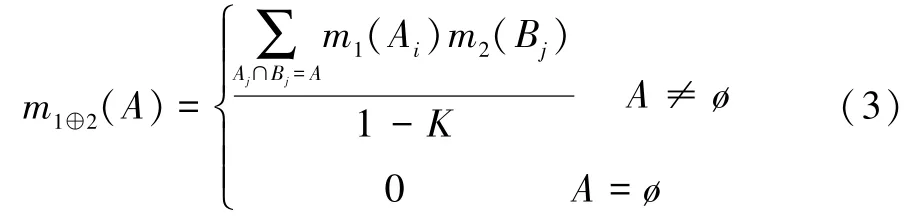
2 D⁃S证据理论的不足和现有改进方法

2.1 D⁃S证据理论的不足

当面临高度冲突的情况时，经典D⁃S证据理论的组合规则将不再适用。如下列1-3。

例1 “0”信任悖论：

设m1（A）＝0.9，m1（B）＝0.1；m2（A）＝0，m2（B）＝1；m3（A）＝0.98，m3（B）＝0.02。使用Dempster组合规则，融合结果为：m（A）＝0，m（B）＝1。

两个证据中A的概率都比较高，而融合结果中A的概率为0，显然有悖常理。

例2 “1”信任悖论：

设m1（A）＝0.01，m1（B）＝0.99，m1（C）＝0；m2（A）＝0.01，m2（B）＝0，m2（C）＝0.99。使用Dempster组合规则，融合结果为：m（A）＝1，m（B）＝m（C）＝0

证据支持率非常低的假设反而获得了完全信任分配，这显然是不符合实际的。

例3 全冲突悖论：设m1（A）＝1，m1（B）＝0；m2（A）＝0，m2（B）＝1。

K＝1，证据完全冲突，无法对证据进行合成。

2.2 现有的改进方法

现有的改进方法一般分为两类：一类是对组合规则的改进，一类是对融合模型的改进。其中，在对组合规则的改进方面，1989年，Yager［5］提出一种改进的组合规则，但它对冲突证据完全否定，而且当处理两个以上证据源时，结果也不理想。2000年，孙全［6］提出了加权合成公式，引入了证据两两之间冲突程度的参数、证据可信度的参数和证据平均支持度，虽然在冲突概率分配上更优越了，但由于分配结果以未知项概率为主导，处理冲突的效果不佳。还有较多学者在组合规则上提出了改进的方法，但这些方法通常不满足结合性，也没有对组合规则进行简化，计算量大而且分配精度低。在对融合模型的改进方面，2000年，Murphy［7］提出了组合之前的平均证据方法，用可信度函数表现不确定性，并对证据的基本概率进行平均，再用D⁃S组合规则进行融合，该方法对冲突证据处理的效果明显，但未对各个证据之间相互的关联性进行考虑。2004年，邓勇［8］对Murphy的方法进行了改进，通过计算各个证据之间的距离来确定证据的支持度与可信度，再用可信度作为权值进行证据的加权平均，最后利用D⁃S组合规则进行证据信息的融合，该方法不仅拥有Murphy方法的所有优点，而且考虑了证据间的关联性，提高了抗干扰能力，但该方法没有考虑证据本身自有的可信度。后续有较多学者在这些基础上对方法进行了各种各样的改进［9⁃12］，文献［9］通过模糊集理论来构造隶属度函数以得到BPA函数，再运用改进的证据组合方法进行证据融合；文献［10］利用平均距离得到证据的权重，并采用哈夫曼树进行证据的加权平均，最后用D⁃S组合规则进行融合；文献［11］引入了冲突比例因子来决定证据的修正方法，并利用证据相似度对其进行局部或者全局的修正；文献［12］引入证据平均值概念，通过各证据与证据平均值之间的距离来得到证据的可信度并作为其权重，但这些方法都存在一些问题。本文在Murphy和邓勇的研究基础上，通过引入信息熵来计算证据的不确定性，对证据本身自有的可信度进行分析，并对权值进行修正，使融合结果更加合理。

3 新的改进方法

3.1 基本概念

定义4 设Θ为一个包含n个两两不同命题的识别框架，ER（Θ）是Θ所有子集生成的空间。m1和m2是在证据源E1和E2在识别框架Θ上的两个基本信任分配函数，对应焦元分别为Ai和Bj，采用Jousselme提出的证据间距离函数［13］来计算m1和m2的距离：

式中，D为一个2n×2n的矩阵，矩阵中的元素为

为了方便计算，式（4）可以转变为

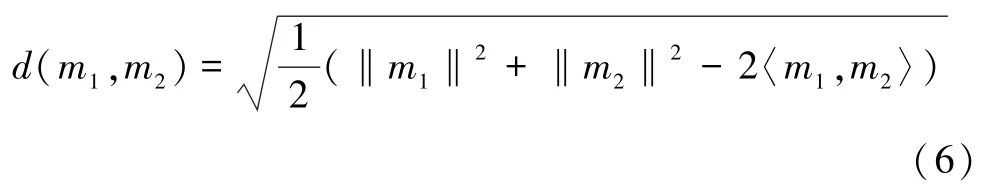
式中，‖m1‖2＝〈m1，m1〉，‖m2‖2＝〈m2，m2〉。

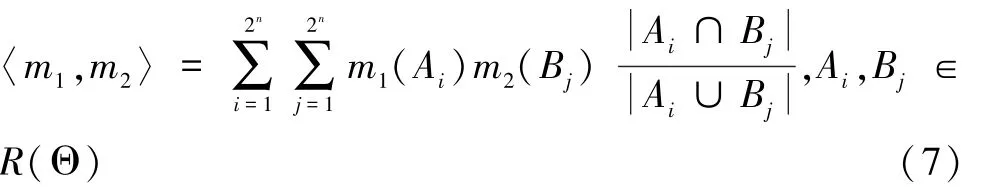
设拥有的证据数目为n，利用式（6）计算可得证据体mi和mj两两之间的证据距离，并表示成一个距离矩阵：

证据体mi和mj之间的相似性测度表示为

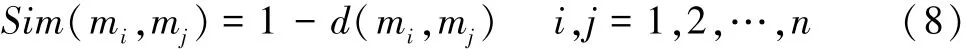
则证据间的相似程度可用一个相似矩阵表示：

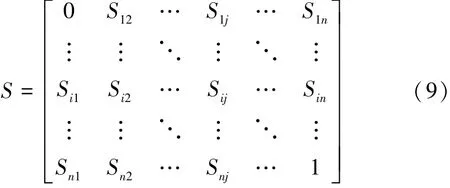
定义mi的支持度为

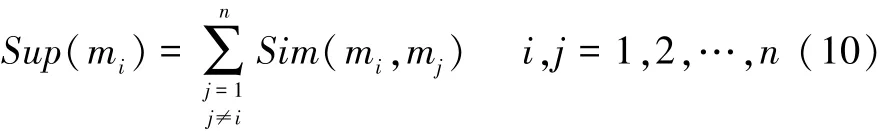
从式（10）可以看出，支持度Sup（mi）反映的是mi被其它证据所支持的程度。两个证据之间的相似度越高，其互相支持的程度就越大。反之，相似度越低互相支持的程度也越低。

将支持度进行归一化可得到可信度：

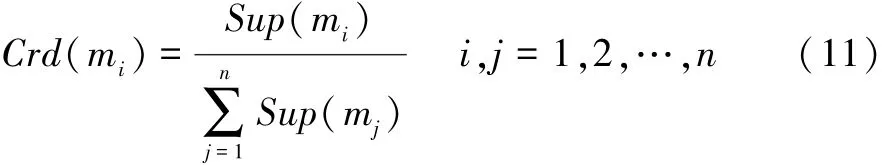
定义5 已知由n个信息源产生证据，有假设集P＝｛｛P1｝，｛P2｝，…，｛PM｝｝，有n个证据mi＝（m1，i，…，mM，i）（i＝1，2，…，n），满足

则第i个证据的信息熵［14］表示为

信息熵反映证据中所含信息量的多少。某条证据的信息熵越大，代表其不确定性也越大；反之信息熵越小，所获得不确定性越小。但是证据的信息熵并不能判断证据之间是否冲突，直接拿信息熵来计算权值可能会使来自被干扰的证据源的证据在融合时比重增加，导致结果不合理。

3.2 改进的方法

本文的方法主要在Murphy和邓勇的研究基础上，对证据的可信度进行修正，步骤如下：

Step1：用式（6）分别计算收集到的n个证据两两之间的距离d。

Step2：用式（8）计算这些证据两两之间的相似性Sim。

Step3：用式（10）、（11）分别计算各个证据的支持度Sup和可信度Crd。

Step4：对可信度进行修正，具体修正过程如下：

转发“锦鲤”求好运、心态平和活得“佛系”，多对他人“skr”点赞，少做“杠精”；既然“确认过眼神”，就要大方“官宣”，“土味情话”更要“皮一下”；时刻“燃烧我的卡路里”，准备“C位”出道！

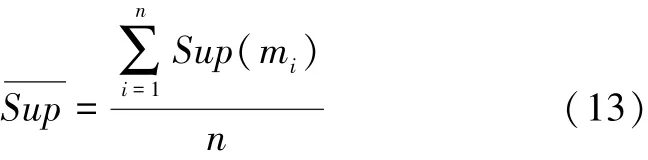
2）定义支持度Sup大于平均支持度的证据为较可信证据。选出所有的较可信证据El（l＝1，2…，S），并用式（12）计算这些证据各自的信息熵I。

3）求取较可信证据的确定指数，定义第t个证据的确定指数λt为

4）求取被选证据集合中证据的修正系数，第t个证据的修正系数φt表示为

5）对所选证据的可信度进行修正，第t个证据修正后的可信度表示为

将修正后的可信度代替所选证据原来的可信度，即Crdt＝Crd′t。

Step5：将可信度作为权重，对所有证据的基本信任分配进行加权平均。

Step6：利用Dempster组合规则对加权平均证据进行n-1次组合，得到融合结果。

4 数值算例

4.1 对合成悖论的解决

例子同上文。

例1 “0”信任悖论：

使用本文方法进行融合：

计算证据间距离：d（m1，m2）＝0.9，d（m1，m3）＝0.08，d（m2，m3）＝0.98；

计算证据相似性：Sim（m1，m2）＝0.1，Sim（m1，m3）＝0.92，Sim（m2，m3）＝0.02；

计算支持度：Sup（m1）＝1.02，Sup（m2）＝0.12，Sup（m3）＝0.94；

计算可信度：Crd（m1）＝0.490，Crd（m2）＝0.058，Crd（m3）＝0.452；

则证据1和证据3为较可信证据，对它们的可信度进行修正；

计算信息熵：I1＝0.141，I3＝0.043；

计算修正系数：φ1＝（1-0.141）／（2-0.141-0.043）＝0.473，φ2＝0.527；

修正可信度：Crd′1＝（0.490+0.452）＝0.465，Crd′3＝0.477；

则权重为：α1＝0.465，α2＝0.058，α3＝0.477；

使用Dempster组合规则对加权平均证据进行进行n-1次组合；

融合结果为m1（A）＝0.998，m2（B）＝0.002。

例2 “1”信任悖论：

使用本文方法，融合结果为：m（A）＝0.0002，m（B）＝m（C）＝0.4999。

例3 全冲突悖论：

使用本文方法，融合结果为m1（A）＝0.5，m2（B）＝0.5。

从以上几例可以看出，本文改进的方法可以较好地对几种典型的证据冲突情况进行处理，使融合结果更加符合实际。

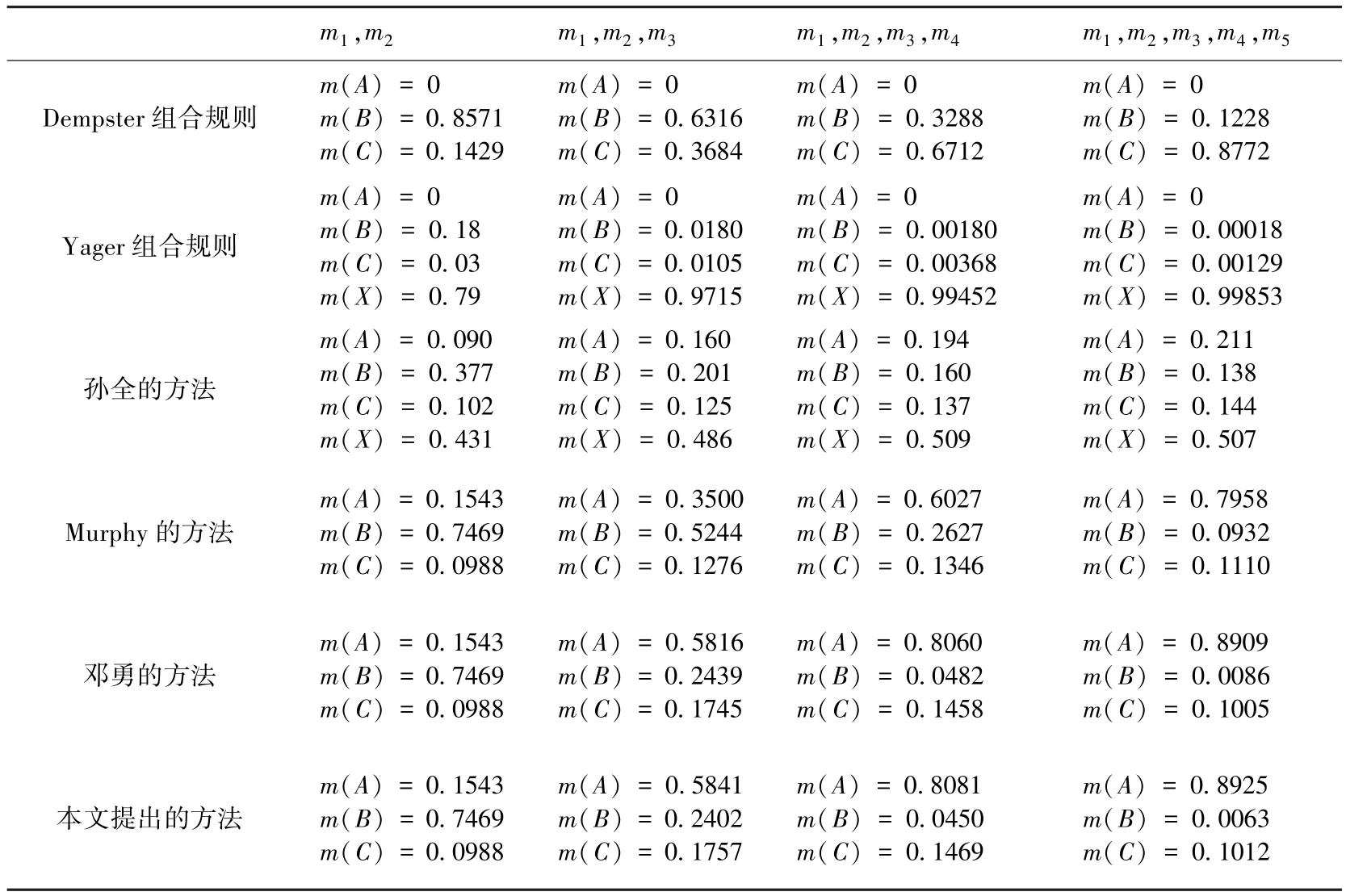
表1 几种证据合成方法的比较

各个方法的融合结果如表1所示。从表中可以看出Dempster组合规则无法有效合成冲突证据；Yager组合规则和文献［6］的方法解决冲突的效果也不佳；文献［7］和［8］的方法明显改善了对冲突证据的处理效果。本文的方法继承了文献［7］和［8］方法的所有优点，并可以有效处理冲突证据，而且计算过程考虑了证据本身的不确定性，使方法收敛更快，抗干扰能力更强，融合结果更合理。

但是由于例4中的较可信证据的信息熵基本一致，导致对证据的可信度修正不明显，最后融合效果的提升较小。为此，下面用一个简单的算例来试验，在较可信证据的信息熵差距较大的情况下，方法的改善效果。

4.2 与现有方法的比较

本文给出一个算例［8］，分别用Dempster组合规则［4］、Yager组合规则［5］、文献［6］的方法、文献［7］的方法、文献［8］的方法以及本文提出的改进方法对算例中的证据进行融合，通过比较融合结果来验证本文方法的有效性。

例4 设识别框架Θ＝｛A，B，C｝，五组证据的基本概率分配如下：

m1：m1（A）＝0.5，m1（B）＝0.2，m1（C）＝0.3

m2：m2（A）＝0，m1（B）＝0.9，m1（C）＝0.1

m3：m3（A）＝0.55，m3（B）＝0.1，m3（C）＝0.35

m4：m4（A）＝0.55，m4（B）＝0.1，m4（C）＝0.35

m5：m5（A）＝0.55，m5（B）＝0.1，m5（C）＝0.35

例5 设识别框架Θ＝｛A，B，C｝，三组证据的基本概率分配如下：

m1：m1（A）＝0.9，m1（B）＝0.1，m1（C）＝0

m2：m2（A）＝0，m1（B）＝0.9，m1（C）＝0.1

m3：m3（A）＝0.6，m3（B）＝0.1，m3（C）＝0.3

文献［8］方法融合结果：m（A）＝0.9187，m（B）＝0.0672，m（C）＝0.0141。

本文方法融合结果：m（A）＝0.9301，m（B）＝0.0616，m（C）＝0.0083。

结果表明，当冲突证据的信息熵差距较大时，本文方法改善效果更好。

5 结束语

现代战场环境复杂多变，敌我双方的信息对抗手段多样，在这样恶劣的自然环境和复杂的电磁环境下，获得的证据之间常常有较大的冲突，使融合结果与实际不符。本文在文献［7⁃8］方法的基础上，提出了一种改进的加权组合算法，通过证据自身的信息熵对较可信证据的可信度进行了修正，方法同时考虑了证据间的关联性和证据本身的可信程度，不仅能有效处理冲突证据，而且提高了在复杂环境下的抗干扰能力，使融合结果更加符合实际。

［1］ Basir O，Yuan X H.Engine fault diagnosis based on rrmlti⁃sensor information fusion using Dempster⁃Shafer evi⁃dence theory［J］.Information Fusion，2007，8（4）：379⁃386.

［2］ Lin T C.Partition belief median filter based on Dempster⁃Shafertheoryforimageprocessing［J］.Pattern Recognition，2008，41（1）：139⁃151.

［3］ Yager R R.Comparing approximate reasoning and proba⁃bilistic reasoning using the Dempster⁃Shafer framework［J］.International Journal of Approximate Reasoning，2009，50（5）：812⁃821.

［4］ Dempster A P.Upper and lower probabilities induced by a multi⁃valued mapping［J］.Annual Math Statist，1967，38（2）：325⁃339.

［5］ Yager R R.On the Dempster⁃Shafer framework and new combination rules［J］.Information Science，1987，41（2）：93⁃137.

［6］ 孙全，叶秀清，顾伟康.一种新的基于证据理论的合成公式［J］.电子学报，2000，28（8）：117⁃119.

［7］ Murphy C K，Combining belief functions when evidence conflicts［J］.Decision support systems，2000，29（1）：1⁃9.

［8］ 邓勇，施文康，朱振福.一种有效处理冲突证据的组合规则［J］.红外与毫米波学报，2004，23（1）：27⁃32.

［9］ 吴强，姜礼平，季傲.基于模糊集和D⁃S证据理论的空中作战目标识别［J］.指挥控制与仿真，2015，37（4）：54⁃58.

［10］曹洁，孟兴.一种有效解决D⁃S理论冲突证据合成的方法［J］.计算机应用研究，2012，29（5）：1815⁃1817.

［11］刘希亮，陈桂明.一种改进的证据合成方法［J］.计算机应用研究，2013，30（9）：2668⁃2671.

［12］苏艳琴，张光轶，徐廷学.一种改进的有效冲突证据融合方法［J］.科学技术与工程，2014，14（12）：217⁃217.

［13］Jousselme A L，Grenier D，Bosse E.A new distance between two bodies of evidence［J］.Information fusion，2001，2（1）：91⁃101.

［14］聂小斯.一种结合信息熵的改进证据分类合成方法［D］.南昌：江西师范大学，2015.

Combination Method of Eidence Based on Distance of Evidence and Information Entropy

JIN Xiao⁃bin，XU Da⁃qin，TAN Liang
（Naval Command College，Nanjing 211800，China）

In order to combine highly conflict evidence more efficiently，an improved method based on the distance of the bodies of evidence was proposed.Firstly，it computed the distance between the bodies of evidence and obtained the support degree and the credibility of each evidence.Then，information entropy was introduced，the correction factor was computed and the credibility of the evidence which had better support degree was corrected.Finally，the credibility was taken as weights and weighted averaging all the evidence，and the Dempster combination rule was used to realize information fusion.The valid⁃ity of the approach was demonstrated by simulation example.

evidence theory；conflict evidence；distance of evidence；information entropy

TP391；E911

A

10.3969／j.issn.1673⁃3819.2016.06.024

1673⁃3819（2016）06⁃0113⁃05

2016⁃08⁃30

2016⁃09⁃24

军事类研究生资助课题（2014JY437）

金晓斌（1991⁃），男，浙江金华人，硕士研究生，研究方向为信息对抗理论与技术。

许大琴（1970⁃），女，副教授。

谈 亮（1970⁃），男，副教授。