联合作战目标协同模型构建与求解方法∗

张 宪，许瑞明

（1.军事科学院联合作战研究实验中心，北京 100091；2.96401部队，陕西宝鸡 721006）

联合作战目标协同模型构建与求解方法∗

张 宪1，2，许瑞明1

（1.军事科学院联合作战研究实验中心，北京 100091；2.96401部队，陕西宝鸡 721006）

在对联合作战目标协同研究内容分析的基础上，提出了多任务部队与多作战目标的协同目标分配模型，其融合了目标综合价值、目标打击有效性、目标威胁适配度、目标类型匹配、目标距离匹配等因素。通过对各因素量化并将协同目标分配模型转换为指派问题进行求解，验证了分析方法的可行性。

协同目标分配模型；指派问题；匈牙利算法

信息化条件下的联合作战中，参战军兵种多、作战要素复杂、敌我对抗激烈，如何有效组织诸军兵种实施协同目标打击是作战筹划阶段需要解决的重要问题。尤其在任务部队种类繁多、作战能力不一，而敌方作战体系目标复杂、相互之间存在复杂关联关系的情况下，单纯采取定性分析或者人工推算不仅耗时耗力，而且分配方案的动态适应性也不强。对任务部队和作战目标特性进行抽取，构建协同目标分配模型，将其转化为指派问题进行求解，不仅能有效降低问题求解难度，而且能快速完成任务部队与作战目标的匹配计算，同时能够为联合作战指挥员有效实施联合作战目标打击提供重要的决策参照。

1 联合作战目标协同

1.1 基本概念

目标协同是一种重要的组织协同方法。它是根据任务部队的作战能力，目标的性质、位置、数量、重要程度和防护情况等，合理分配目标，组织协同动作［1］。区分目标组织协同，需要联合作战指挥员对作战目标体系进行合理分类，根据前期情报进行综合研判，完成目标重要性和关联性分析，综合考虑敌我双方作战能力对比关系，完成两者之间的匹配，合理确定打击对象。

1.2 作战原则

联合作战目标协同作战过程中，必须强调任务部队、作战能力、作战目标三者之间的动态优化匹配，其坚持以下原则：

1）能力适配原则。即在对任务部队指定打击目标的过程中，必须与部队的作战能力相适应，不能给部队指定超出其作战能力之外的作战目标。

2）效益优先原则。在对目标实施打击过程中，要立足取得最大作战效益，优先打击敌方关键节点目标。

3）动态适应原则。要考虑战场态势的动态变化，关注敌我双方作战能力的动态变化，完成两者之间的匹配计算。

4）威胁权衡原则。要考虑敌方目标体系对我方作战能力的威胁程度，争取以最低的风险完成目标打击任务。

1.3 分析流程

联合作战目标协同分析流程如图1所示。首先构建多任务部队和多作战目标的协同目标分配模型，给出作战能力等效计算方法，然后基于战场目标属性和本方部队作战能力计算给出距离匹配系数、类型匹配系数、打击有效性系数和目标威胁匹配系数，从目标综合价值合成的角度对目标价值进行分析，最后将协同目标分配问题转化为指派问题并进行求解分析。

2 协同目标分配模型构建

目标协同作战过程中，可基于一定的准则优先选择作战效益最佳的任务部队和作战目标匹配，将两者最优匹配程度以综合匹配度的形式添加到目标函数中，构建优化模型进行求解分析。综合匹配度函数与任务部队与作战目标的距离、任务部队能否有效打击目标、任务部队能否有效毁伤目标、任务部队受威胁程度以及目标的综合价值等因素直接相关［2］。

图1 目标协同作战流程分析

2.1 协同目标分配模型的提出

设定作战部队数量为m，编号分别为force1，force2，…，forcem，作战目标数量为n，编号分别为tgt1，tgt2，…，tgtn。它们之间的综合匹配度函数为ω（i，j）＝ω（forcei，记任务部队forcei与作战目标tgtj之间的距离匹配系数矩阵为（sij）m×n，类型匹配系数矩阵为（mij）m×n，打击有效性系数矩阵为（fij）m×n，目标威胁匹配系数矩阵为（hij）m×n，各战场目标的价值矩阵为（vj）n×1。假定两者的权重分别为α，β，则有ω（i，j）＝α（sij·mij·fij）+βhij。

令φ（i，j）为两者之间的对应关系函数，则有

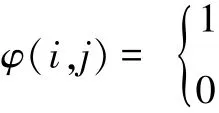
任务部队forcei与作战目标tgtj对应

任务部队forcei与作战目标tgtj不对应。

当任务部队与作战目标数量相同时，可划归标准指派问题（Standard Assignment Problem）进行求解。当两者数量不等时，可将其归结为GAP（Generalized As⁃signment Problem）问题进行求解分析。设Φ、Φ′和Φ″分别为任务部队数量等于、大于和小于作战目标数量下的目标函数，则有：

1）任务部队与作战目标数量相同（m＝n）

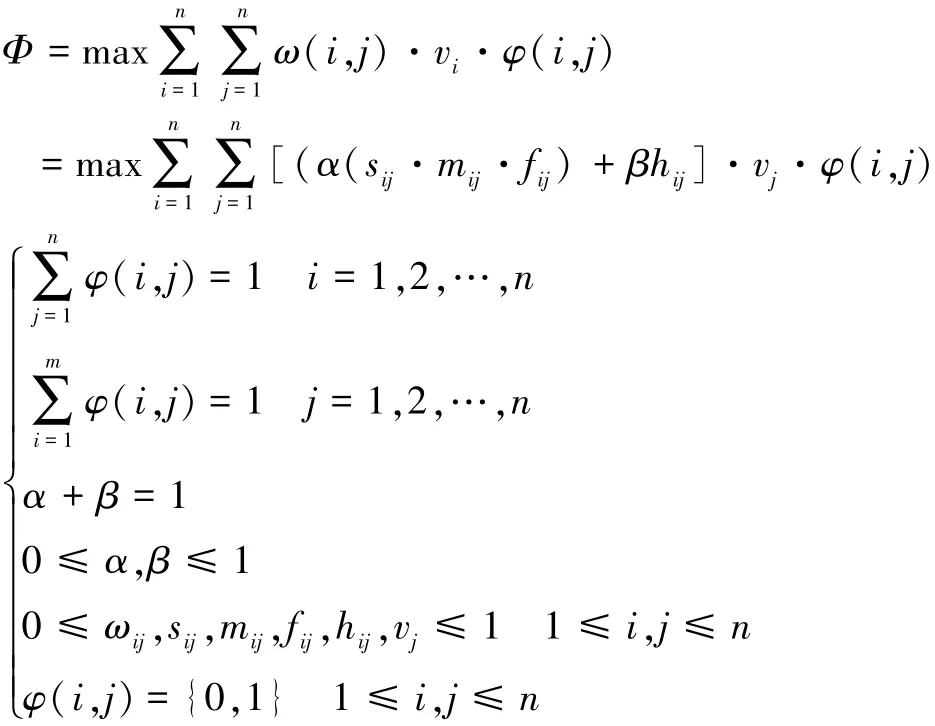
2）任务部队数量大于作战目标数量（m＞n）

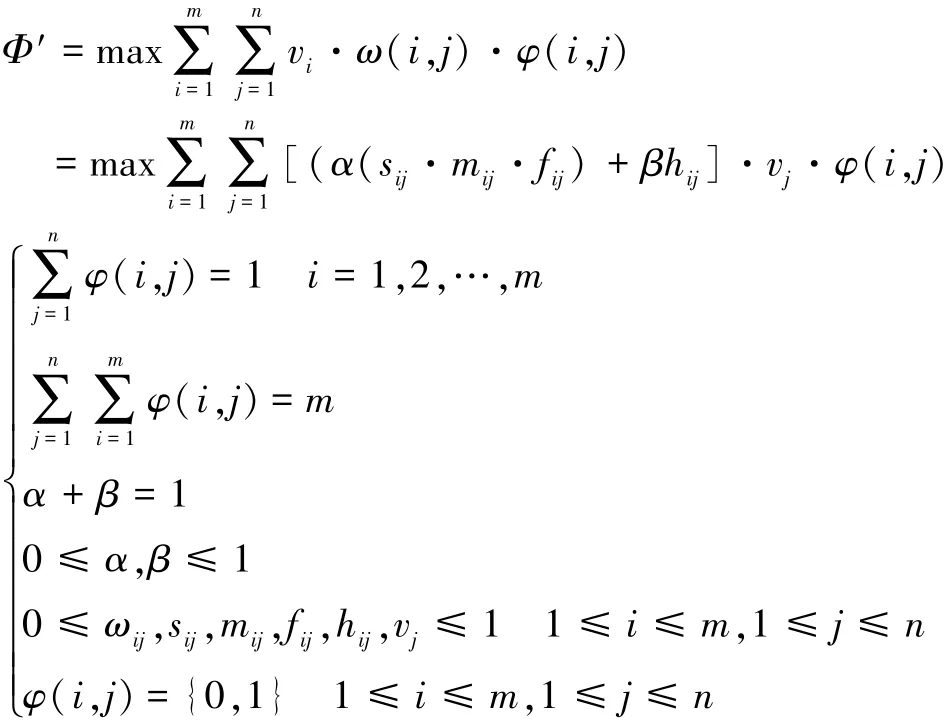
3）任务部队数量小于作战目标（m＜n）

2.2 相关参数定义与计算

1）距离匹配系数

假定任务部队forcei武器装备型号有s种，分别为equip1，equip2，…equips，各型装备的最小作战距离为dmin，1，dmin，2，…，dmin，s，最大作战距离为dmax，1，dmax，2，…，dmax，s，各型武器装备占所有武器装备的百分比为percent1，percent2，…，percents，则任务部队的平均射程dmean，i可表示为dmean，i＝（dmin，i+dmax，j）·percenti。

设任务部队forcei的展开半径为rfi，目标tgtj的幅员半径为rtj，dij为作战部队forcei与目标tgtj之间的距离为两者中心间的距离，任务部队和作战目标之间的最大距离为d′ij，最小距离为d″ij，则距离匹配系数sij可表示为：

2）类型匹配系数

如果任务部队forcei中equipi能够对目标tgtj造成有效毁伤，则类型匹配系数为1，否则为0。一般地有

3）打击有效性系数

假定在类型匹配的情况下，任务部队的等效作战能力指数为pi，其对目标tgtj造成有效毁伤的最小阈值为smin，最大毁伤阈值为smax，则

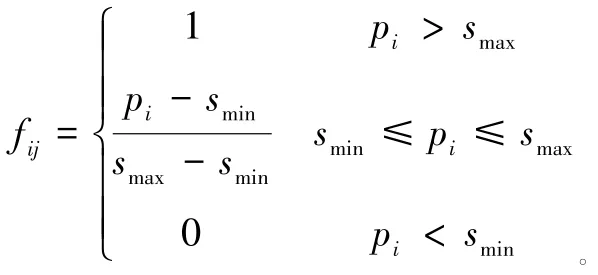
4）目标威胁匹配系数

记任务部队与目标之间的距离为dij，作战目标的有效作战距离为dtgti。当dij＞dtgti，则目标对任务威胁指数为0，否则距离匹配系数为1。记powerj为目标tgtj对部队forcei造成毁伤的等效作战能力指数，［indexi-，indexi+］为目标能够对部队造成有效毁伤的上下限，如目标tgtj对作战部队forcei形成不了威胁，则威胁匹配系数为0；如果形成致命威胁，则匹配系数为1。则目标威胁匹配系数可表示为：

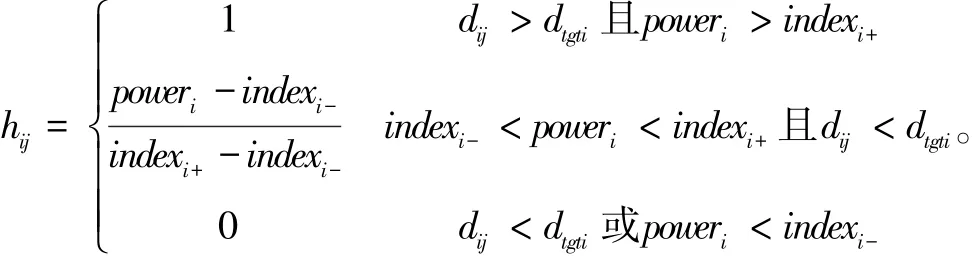
5）目标综合价值

目标综合价值分析是将单目标价值分析和目标网络价值分析以适当的形式进行合成运算而得到的有关目标价值的表示形式。设单目标价值分析中各目标节点的价值分别为value1，value2，…，valuen，目标网络价值分别为Nvalue1，Nvalue2，…，Nvaluen，则目标i的综合价值可表示为Vali＝α1·valuei+β1·Nvaluei，其中α1+ β1＝1，0≤α1，β1≤1。通常取α1＝β1＝0.5。用上面的公式可以对战场所有目标进行价值分析和排序。

①单目标价值分析

对单目标进行价值分析可以采取如图2所示的评价指标体系。涉及6个一级指标，分别是：目标固有价值性、目标潜在价值性、任务一致性、对敌有利性、打击风险性和目标易损性。

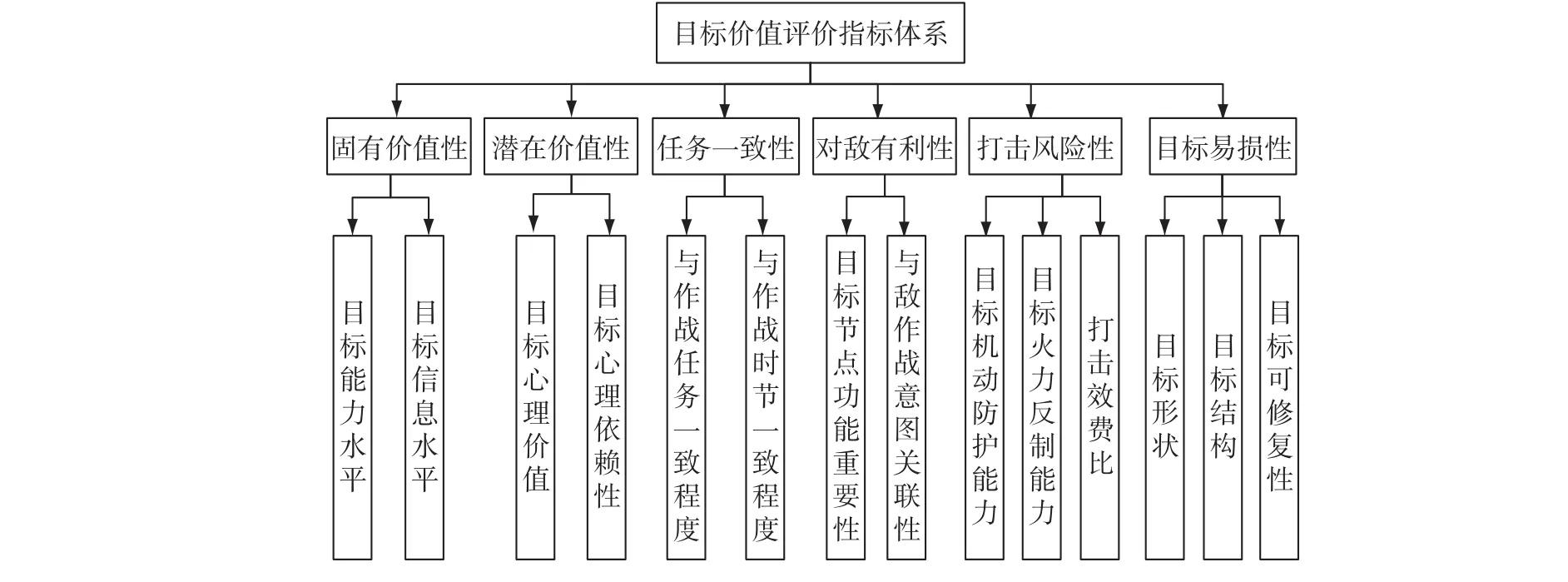
图2 目标价值评价指标体系

对单目标价值分析实质上是对多个属性进行合成的过程，可以将其看成是多属性决策（MADM）问题，采用主客观相结合的Entropy-Topsis方法来分析目标价值。其具体计算流程可见文献［3］。

②目标网络价值分析

记目标网络为G＝（V，E），V＝｛v1，v2，…，vn｝表示目标网络n个节点的集合，E＝｛e1，e2，…em｝表示目标网络m种关联关系的集合。则目标网络图可视为无环无向加权图。考虑到计算时间约束，可采取基于凝聚度的节点重要性计算方法，其计算流程如图3所示［4］。

6）等效作战能力计算及合成

①等效作战能力合成

图3 基于凝聚度的节点重要性计算流程

等效作战能力计算是用相对数值反映分析对象差别的一种量化方法［5⁃6］。通常采用指数法来对不同作战能力进行等效比对。其可分为两个步骤：1）“标准化折算”，2）“作战能力聚合”。

②基准武器战斗力等效计算方法

就多维战场空间而言，陆战场是涉及武器装备类型和数量最多、交战规则和毁伤计算最为复杂的战场空间之一。以陆战场为基准，通过对同类型的武器装备进行归类，可以得到武器装备类别，通常分为步兵、装甲、反坦克、压制、防空、空中突击和其他武器等7大类。就单武器装备而言，在各自类别上选择基准参照，可以计算得到单武器作战能力指数。

不同基准武器换算系数可通过下面公式计算求得

［Cij］＝［Pij］×［Hij］×［Aij］

（i＝1，2，3，…，6；j＝1，2，3，…，6）。

其中，i和j为n种基准武器，［Cij］6×6为比例系数矩阵，［Pij］6×6为作战概率矩阵，［Hij］6×6为毁伤概率矩阵；［Aij］6×6为能力范围矩阵。设步兵战斗力指数为1，通过求解方程组，可以得到各种基准武器间的比例系数。

③作战能力聚合

设任务部队forcei共有N类武器装备，每类武器装备的作战能力指数为Ii，则该型武器的战斗潜力指数为为第i类武器中各种型号的数目，Iij为第i类武器第j个武器的归一化指数，Xij为第i类武器第j个型号武器的数量。

3 协同目标分配模型的求解

协同目标分配模型可以通过将广义指派问题转化为标准指派问题，进而调用标准算法来进行求解分析。

3.1 广义指派问题的转换

对于GAP而言，当m≠n时，虽然可以通过补零将其归结为标准指派问题进行求解，但是其需要计算两次。通过行列扩展，通过一次指派就完成对问题的求解［7⁃8］。

1）部队数大于目标数的转换

当m＞n时，首先从m个部队中选出n个部队来与n个目标一一对应。对剩余m-n个作战部队而言，假定每个部队都存在另外m-n个与之对应的“虚拟目标”，每个人完成这些“等价”工作的效益相同。这样，目标就有n（m-n+1）个，而每个目标最多由一部队来完成，这样就有n（m-n+1）-m＝（m-n）（n-1）个部队，它们的工作效益为0，可将问题转化为标准指派问题。扩展后的损益矩阵为

其中，第一行表示有（m-n+1）个R，第二行表示（m-n）（n-1）行n列的零矩阵。假定扩展损益矩阵求解得到的匹配方案为X＝（xij）h×h，h＝n（m-n+1）。通过统计前m行中等于1的元素，将对应的列数通过mod（n）即可得最终的指派方案。

2）部队数小于目标数的转换

当m＜n时，首先从n个作战目标中选出m个与m个作战部队一一对应。对剩余n-m个目标而言，假定每个目标都存在另外m-n个与之对应的“虚拟部队”，每个部队对应这些“等价”目标的效益相同。这样，部队就有m（n-m+1）个，需要增设虚拟部队m（n-m+ 1）-n＝（n-m）（m-1）个，它们对于每个目标的效益都为0。此时的扩展损益矩阵为

其中，第一列有（n-m+1）个R，第二列表示有m行（n-m）（m-1）列的零矩阵。假定扩展损益矩阵求解得到的匹配方案为X＝（xij）h×h，h＝m（n-m+1），通过统计前n列中等于1的元素，将对应的行通过mod（m）即可得最终的指派方案。

3.2 典则指派问题的求解

由于指派问题结构特殊，人们已经提出许多便捷有效的算法，如匈牙利法、削高排除法、缩阵排除法和差额法等。相比较而言，匈牙利算法应用最为广泛，其能够在多项式时间内完成指派问题的求解。其计算步骤如下：

Step1初始化。判断损益矩阵合理性，排除错误的指派矩阵。

Step2每行产生零元素。调用二进制矩阵函数，使得每行至少有一个零元素。

Step3寻找零元素。对新的损益矩阵求反，获取非零位置并进行记录。

Step4标注零元素。用标注的零元素覆盖每一列，如果所有列都能够被覆盖，对每一列的零元素进行标注，如果所有列都有零元素，则找到最优匹配方案。

Step5寻找非零元素并进行填充。如果在行中包含没有标注的零元素，则跳转到Sep6；否则，用直线将包含标注元素的行划掉，重复这个方式直到所有的零元素都被覆盖，计算并保存最小的未被覆盖的值并直接跳转到Step7。

Step6对零元素进行迭代标注。令Z0表示Step5计算得到的非覆盖的主要零元素，Z1表示Z0中列中标注的零元素，Z2表示Z1行中的零元素，通过迭代使得所有列中不存在没有标注的零元素。对于每一个主要的零元素，擦除矩阵中与其相交的所有的非零元素。然后返回Step4。

Step7对每一个被覆盖行中每一个元素，添加其所在非覆盖最小元素的最小值，然后对每一列减去其对应的元素，在没有任何可以替代或者标注的零元素时返回Step5。

Step8计算得到指派方案。对损益矩阵进行累加，记录并显示所选行和列，得到最终指派方案。

4 算例分析

假定在联合作战某次战术行动中，敌我双方在小范围内进行实体对抗。我方通过周密侦察，已基本得知敌方作战部署和目标类型、点位和毁伤能力。为了以最小代价换取最大作战效益，我方派出6个作战分队对敌方4个作战目标实施协同攻击，各部队的作战能力和可打击目标类型各不相同。我方作战分队分别是：炮兵连1、炮兵连2、坦克连、工兵连、直升机分队1和直升机分队2。敌方作战目标分别是指挥所、防御工事、前沿炮兵阵地和通信枢纽。在前期情报综合研判和综合军事专家意见的基础上，得到的任务部队和作战目标的距离匹配系数矩阵S、类型匹配系数矩阵M、打击有效性系数矩阵H和目标威胁匹配系数矩阵F分别为

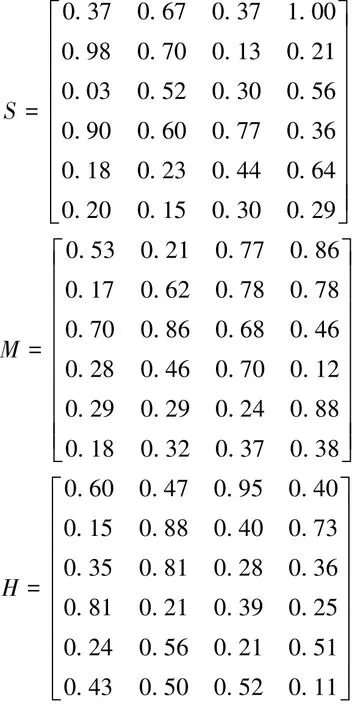
对目标单目标价值和目标网络价值赋予相同的权重，取α1＝β1＝0.5，对4个矩阵进行合成，可得综合匹配矩阵为

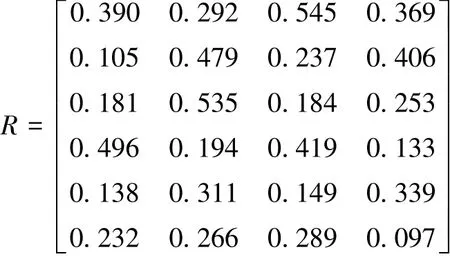
根据单目标价值分析指标体系，结合前期收集数据，运用Entrop⁃topsis法可以得到4个战场目标的综合价值分别为：［0.69，0.84，0.73，0.79］，通过列乘可以得到指派问题的损益矩阵为

寻找矩阵中的最大元素，逐个减去最小元素，形成新的损益矩阵，按照（6-4+1）×4＝12，将矩阵扩展为12×12维，其形如

其中，R′为新的损益矩阵。调用匈牙利算法进行求解，可得指派方案为：1→3，2→2，3→2，4→1，5→4，6→2。即炮兵连1和炮兵连2打击前沿炮兵阵地，直升机分队1和直升机分队2打击指挥所，坦克连打击防御工事，工兵连攻击通信枢纽，基本符合战场实际，经过检验为最优指派方案。

5 结束语

本文基于等效优化思想将联合作战目标协同问题转化为协同目标分配模型进行求解分析。目标优化函数中包含了目标价值分析、目标打击有效性、目标威胁适配度、目标类型匹配系数和目标距离匹配系数等要素。

本方法主要适用于战场目标相对较少，己方作战武器装备杀伤机理基本相同，并且己方武器装备的可区分程度较为明显的情况。优化模型对各种因素的量化方法相对比较简单，尤其在综合匹配度函数中，几种匹配度之间还存在关联关系，用代数方法进行合成不免降低模型的适用性。与此同时，武器装备作战效能等效换算方法的科学性也对本方法的科学性有很大影响。在下一步研究中可以考虑以远程精确打击武器为重点，对目标协同影响因素进行更为精准的考虑，同时考虑对任务部队和目标类型进行更为合理的划分，以提高模型方法的适用性。

［1］ 陈荣弟.联合战斗教程［M］.北京：军事科学出版社，2013：150⁃153.

［2］ 沈寿林，朱江，王三喜，等.联合作战目标武器弹药匹配模型［J］.指挥控制与仿真，2013，35（5）：47⁃50.

［3］ 张宪.基于Entropy⁃Topsis法的海上运动目标价值分析［A］∥体系作战与军事运筹学研究［C］.湖南：国防科技大学出版社，2014.

［4］ 王甲生，吴晓平，廖巍，等.改进的加权复杂网络节点重要度评估方法［J］.计算机工程，2012，38（10）：74⁃76.

［5］ 孙儒凌，韩林，靳小凤.联合作战计算［M］.北京：国防大学出版社，2014：165⁃174.

［6］ 许瑞明.简明军事运筹学教程［M］.北京：军事科学出版社，2013：130⁃135.

［7］ 郭强，孙浩.运筹学原理与算法［M］.北京：科学出版社，2012：214⁃220.

［8］ 王海英，黄强，等.图论算法及其MATLAB实现［M］.北京：北京航空航天大学出版社，2010：34⁃41.

Joint Operational Target Synergy Model and Solving Method

ZHANG Xian1，2，XU Rui⁃ming1
（1.Joint Operation Experimental Research Center of Military Sciences，Beijing 100091；2.96401 Troops，Baoji 721006，China）

Based on the analysis for the joint operational target synergy，the paper proposes the coordinated target assignment model，which consideres the factors of target integrated values，target attack effectiveness，target threat degree，target type match degree and the target distance match degree.By transforming the coordinated target assignment model to AP problems and solving it with the Hungarian algorithm，the feasibility of the method is verified.

coordinated target assignment model；assignment problem；Hungarian algorithms

E211

A

10.3969／j.issn.1673⁃3819.2016.06.006

1673⁃3819（2016）06⁃0026⁃05

2016⁃08⁃01

2016⁃10⁃13

全军军事类研究生资助课题为2014JY638

张 宪（1983⁃），男，陕西泾阳人，工程师，博士，研究方向为军事系统建模与仿真。

许瑞明（1963⁃），男，研究员，博士生导师。