序爆子弹降低抛撒后相互殉爆可能的时序优化排布*

蔡泓杰,闻 泉,王雨时,张志彪

(南京理工大学机械工程学院,南京 210094)



序爆子弹降低抛撒后相互殉爆可能的时序优化排布*

蔡泓杰,闻 泉,王雨时,张志彪

(南京理工大学机械工程学院,南京 210094)

针对水中序爆子弹抛撒后间距过小可能相互殉爆或影响工作性能的问题,通过陆上抛撒试验落点坐标数据统计分析,得到子弹抛撒后距离分布。不相邻子弹抛撒后距离均值多显著大于相邻子弹,且子弹层距越大,抛撒后两层子弹间距离均值也越大。据此进行了母弹内同层子弹和不同层间子弹装配时序优化排布,以有利于降低子弹抛撒后相互殉爆和因爆炸冲击引起的机械结构或电路失效的可能性,提高子弹正常工作概率。

子母弹;蒙特卡罗方法;设计方案;时序优化排布;威布尔分布

0 引言

子弹群落点分布形状、大小及均匀程度直接影响子母弹毁伤效果。子母弹总体设计时需确定子弹在弹舱内的布局和抛撒方式,并通过母弹与子弹运动方程计算子弹的空中运动轨迹和落点分布情况[1]。由于风向和子弹空气动力学特性等影响,实际子弹分布与理论值存在偏差。若抛撒后子弹间距过小,子弹起爆时可能殉爆相邻子弹,子弹爆炸也会使较近的子弹壳体发生较大变形,对子弹及其引信的机械结构和电子器件等造成损毁,从而导致子弹群无法按预定时序起爆,影响母弹作用效果[2]。

文献[3]据水中爆炸特点,建立了一种利用冲击波峰值压力和气泡周期判断水中殉爆的试验方法,可确定炸药装药殉爆距离、殉爆安全距离以及被发装药殉爆反应程度,并通过水中爆炸试验得到验证。文献[4]选取水下典型主发装药与被发装药模型,采用有限元软件ANSYS/LS-DYNA模拟典型带壳装药的水下殉爆并开展了水下殉爆试验研究,得到水下殉爆距离和安全距离。文献[5]通过对圆形、正方形和正六边形3种横截面形状子弹各种布局方式具体方案计算、对比和筛选,得到不同子弹个数时装填密度最大的子弹截面形状和布局。

目前子弹排布只考虑了母弹中子弹装填密度最大化的几何学问题,并未将每一枚子弹在母弹中的具体位置对母弹整体性能的影响考虑在内。由于子弹装入母弹前按子弹编号依次设定起爆时间,所以预先对子弹进行排列可使装配完成时相邻子弹的起爆时间间隔增大,进而使整发母弹内相邻子弹抛撒后起爆时间间隔增大,并使相邻起爆时间子弹的空间距离增大,从而降低子弹殉爆和内部结构损毁的可能性。文中针对此问题,提出了序爆子弹降低抛撒后相互殉爆可能性的起爆时序优化排布。

1 等间距顺序爆炸子弹群工作原理及抛撒试验

某子母弹子弹采用离心方式抛撒,利用母弹的旋转使子弹在一定范围内撒布开,从而以一定速度从一定高度落入水中并按设定的起爆时刻起爆。但离心转速较低,约25 r/s。该子母弹由15层子弹组成,每层有30枚子弹。子弹装入母弹前对子弹编号并依据编号设定起爆时刻。设定1号子弹起爆时刻为t,其它子弹依序号逐枚递增t1,即2号为t+t1,3号为t+2t1,4号为t+3t1,依此类推。母弹中第一层装填1～30号子弹,第二层装填31～60号,第三层装填61～90号子弹,每层顺序装填30枚,依此类推。每一层内30枚子弹按自然行顺序排布,其中第一层子弹排布方式如图1所示,第2层子弹排布方式相当于在第1层排布子弹序号上加30,第3层加60,其余各层排列依此类推。

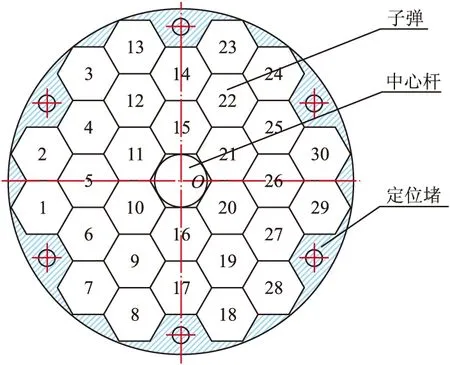
图1 第一层子弹排布方式

2014年10月进行了3发母弹陆上抛撒试验。其中每发母弹装填450枚子弹,共回收到1 307枚,测得其落点坐标数据。

2 试验数据分析

2.1 同层内相邻子弹与不相邻子弹距离数据处理

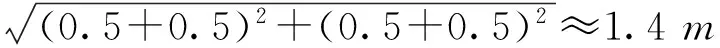
定义装配时在同一层内与某子弹六面任意一面直接接触的子弹为其相邻子弹,其余为不相邻子弹(如图1中11号子弹的相邻子弹为4、5、10、12、15号子弹,其余均为不相邻子弹)。3发母弹各抽取3层(即最外层和中间层,其中3号母弹第十五层落点坐标数据明显有误,改用第十四层)对相邻与不相邻子弹抛撒后落地点距离进行统计分析。抛撒后相邻子弹距离分布直方图如图2所示(以第1号母弹第十五层为例),抛撒后不相邻子弹距离分布如图3所示,统计结果如表1所列。

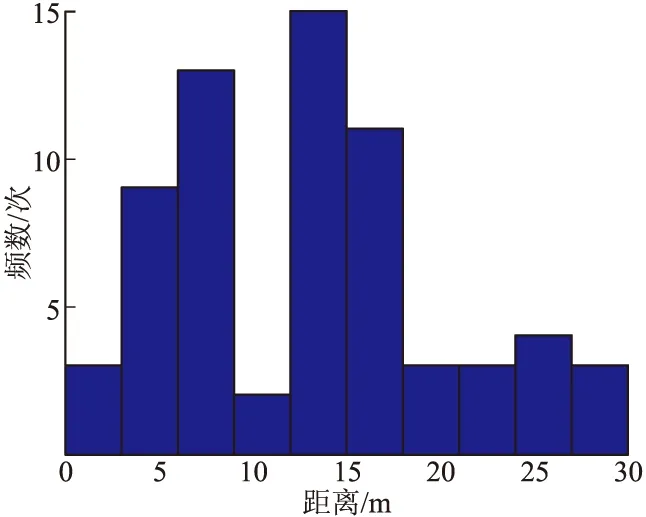
图2 抛撒后相邻子弹距离分布直方图

直接比较均值并应用t检验法进行两数据总体均值的比较检验,分别取显著性水平0.2、0.1和0.05,结果如表2所列。由表2可知,抛撒后不相邻子弹距离均值大于相邻子弹距离,且有46.7%的情形两者具有显著性差异。

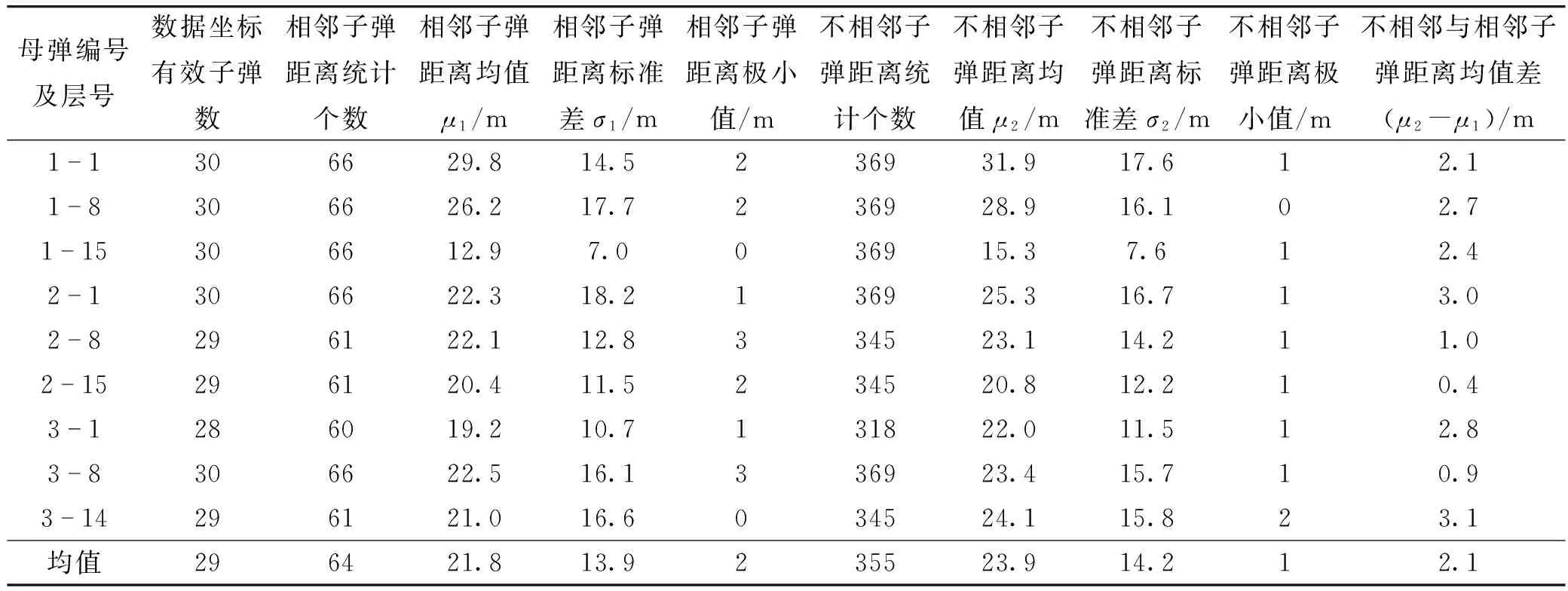
表1 相邻与不相邻子弹间距统计结果

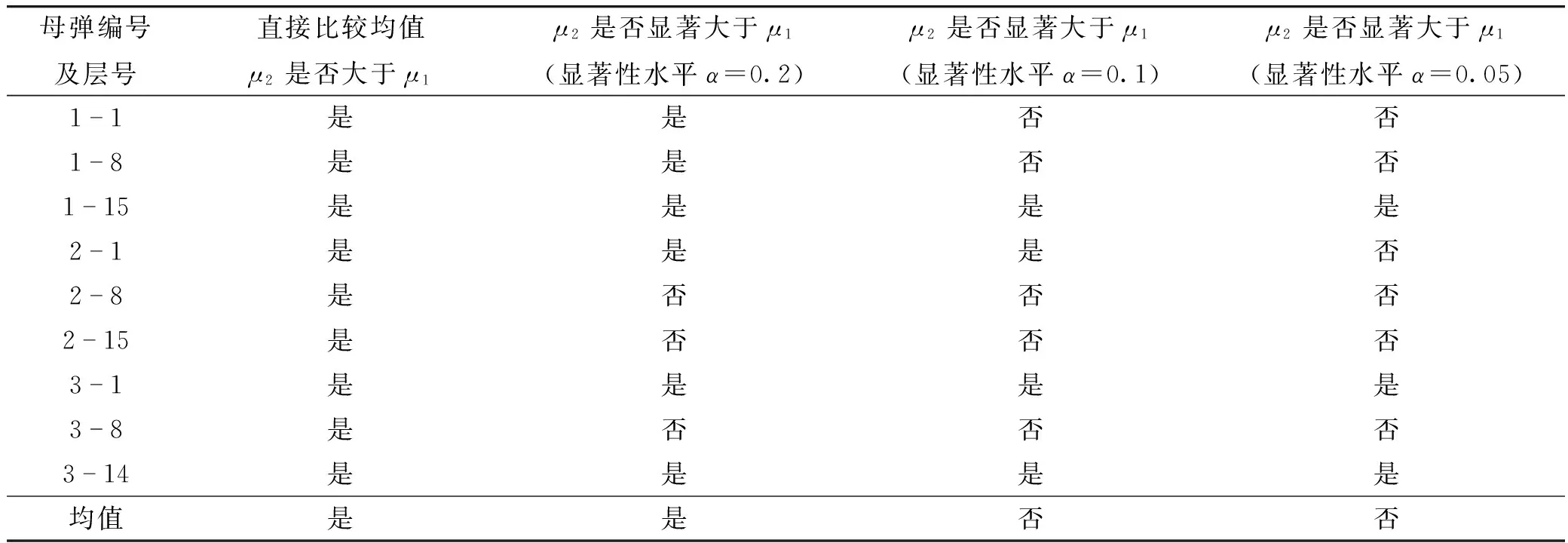
表2 相邻子弹与不相邻子弹距离均值比较检验结果

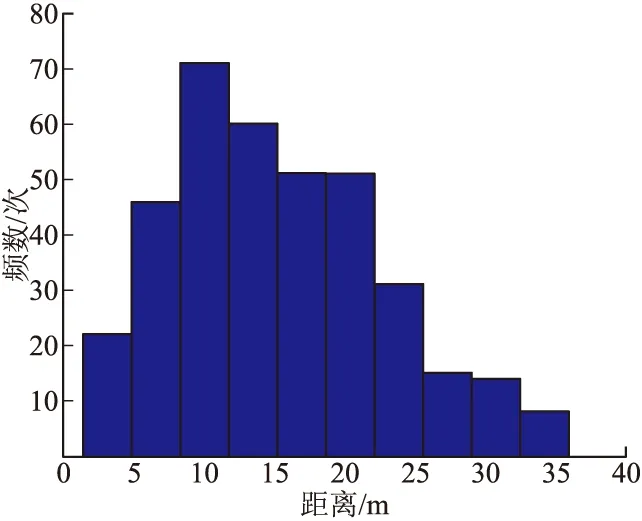
图3 抛撒后不相邻子弹距离分布直方图

2.2 层内距离与不同层间距离数据处理

在3发母弹中,不同层间两枚子弹落点坐标在平面上“重合”的共有119组(数据精度为±0.5 m),其中两层为相邻层的共有18组。相邻两层子弹落点在平面上“重合”,表明其空间距离约为其高(深)度方向距离,若高(深)度方向距离过小,同样也会相互殉爆或因爆炸冲击引起机械结构或电路失效,从而影响子弹正常工作。

将抛撒后某一层内所有子弹(包括相邻与不相邻)间距离作为一个总体进行统计分析,其分布直方图如图4所示(以1号母弹第八层为例)。将抛撒后不同层间所有子弹间的距离进行统计分析,其分布直方图如图5所示(以1号母弹第一层与第八层为例)。层内及不同层间子弹距离统计及分布检验结果如表3所示。

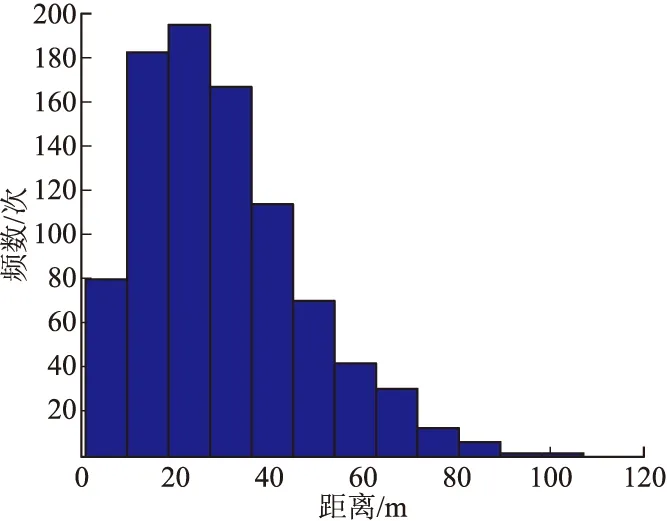
图4 抛撒后层内子弹距离分布直方图

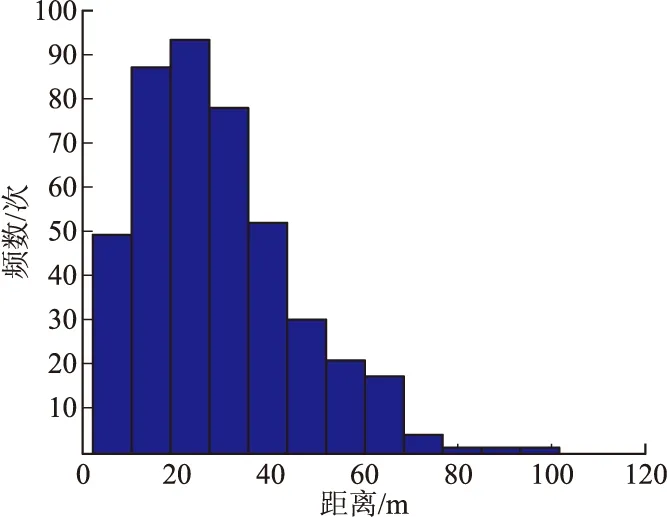
图5 抛撒后不同层间子弹距离分布直方图

应用Matlab中kstest函数进行分布检验,原假设为层内及不同层间子弹距离服从威布尔分布,取显著性水平α=0.05。当p>α时,接受原假设。现Matlab程序求得的p值均大于α,表明所有层内及不同层间子弹距离均服从威布尔分布。

设母弹装配时两层子弹间层数差为Δn,层间子弹距离均值为d,层间子弹距离最小值为dmin,对Δn相等的两组数据(例如第九层和第七层与第八层的Δn相等,其值为1)的均值求平均,得到层数差为Δn时层间子弹距离均值d和最小值dmin。按此方法对上表数据作进一步处理并进行拟合,得到d与Δn的线性函数表达式为d=22.95+0.93Δn,dmin与Δn的函数关系不明确,因此增加该枚母弹第七层和第九层与其余各层间距离最小值数据,得到dmin与Δn的线性函数表达式为dmin=0.17+0.09Δn。d与Δn关系如图6所示,dmin与Δn关系如图7所示。表明每相差一层,距离均值约相差0.93 m,距离最小值约相差0.09 m。

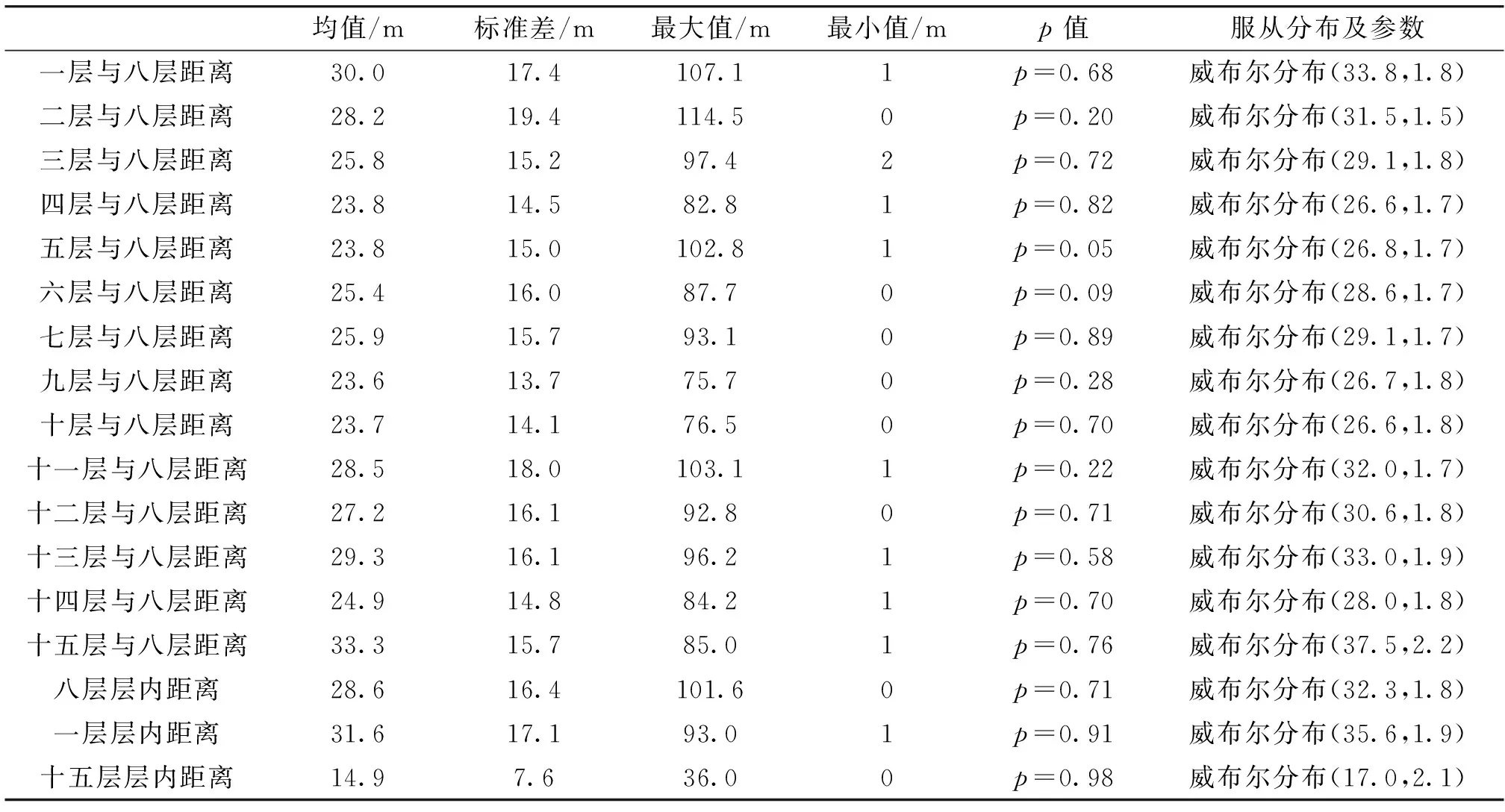
表3 层内及不同层间子弹距离统计结果

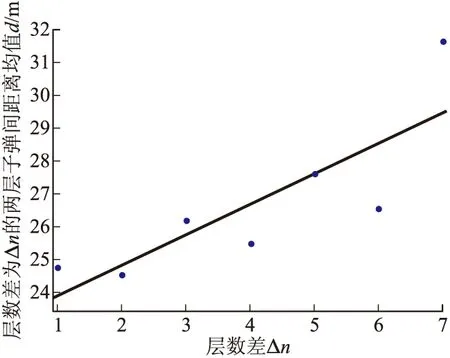
图6 层间子弹距离均值d随层数差Δn的变化

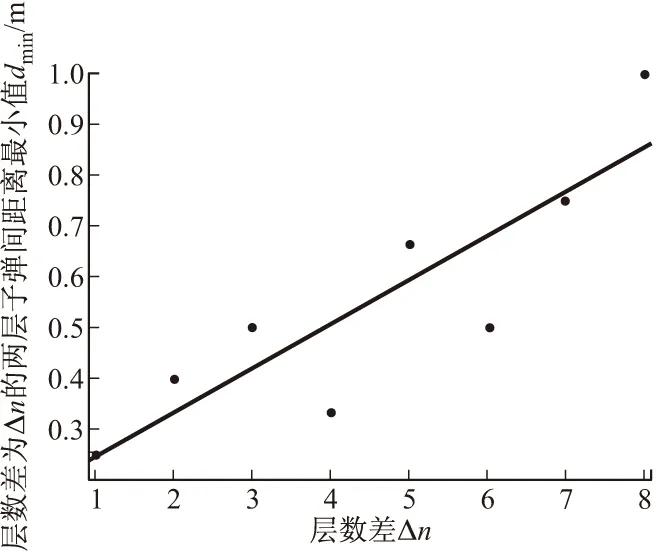
图7 层间子弹距离最小值dmin随层数差Δn的变化

3 子弹排布方式

3.1 同层内子弹排布方式

按图1的方式装填子弹,相邻子弹的起爆间隔时间最小值仅为t1。因此有必要研究层内子弹的排布问题,使得相邻子弹的起爆间隔时间尽可能增大。对于单枚子弹,以11号子弹为例,其相邻子弹序号为4、5、10、12、15,相邻子弹间的起爆间隔时间分别为t1-4,t1-5,t1-10,t1-12,t1-15。由于时间间隔与子弹序号为对应关系,故起爆间隔时间可转换由子弹序号差值的绝对值表示。从上述分析可知,装配时不相邻子弹在抛撒后的间距大于相邻子弹在抛撒后的间距。因此若装配时第i枚子弹序号差值绝对值的最小值为Ni,则通过调整子弹顺序,使所有Ni的最小值尽可能大即可使抛撒后间距较小子弹的起爆间隔时间尽可能大。

运用Matlab软件对层内子弹排序进行蒙特卡罗模拟,随机生成一个1～30的数列代表子弹序号,图1中的1～30代表子弹位置,按上述方法计算,重复上述过程,保留所有使Ni最小值最大的数列,若Ni的最小值相等,则取所有Ni均值较大的一组为较优结果,流程如图8所示。分别计算108次、109次和2×109次,得到较优解相邻子弹间的起爆时间间隔均至少为4t1,但计算108次所得到的结果均值小于计算109次所得到的结果,而计算2×109次所得结果与计算109次所得结果相同,因此,将此组解作为最优结果,如图9所示。该方案中暂定t1=0.5 s,则相邻子弹间的起爆时间间隔至少为4×0.5=2.0 s。

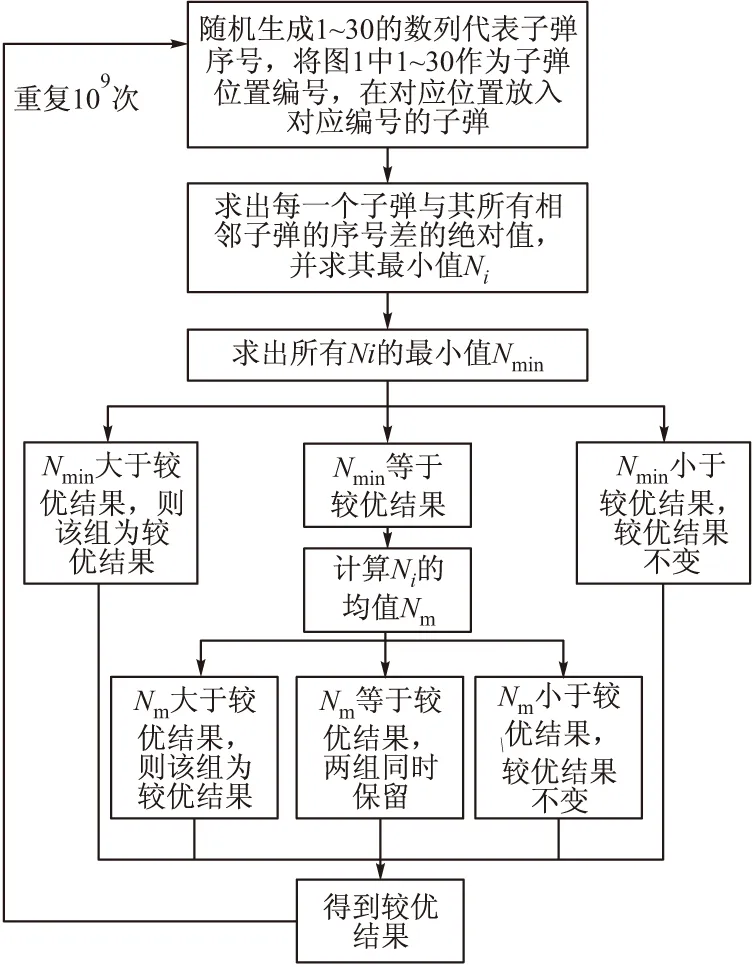
图8 同层内子弹排布计算机优化流程

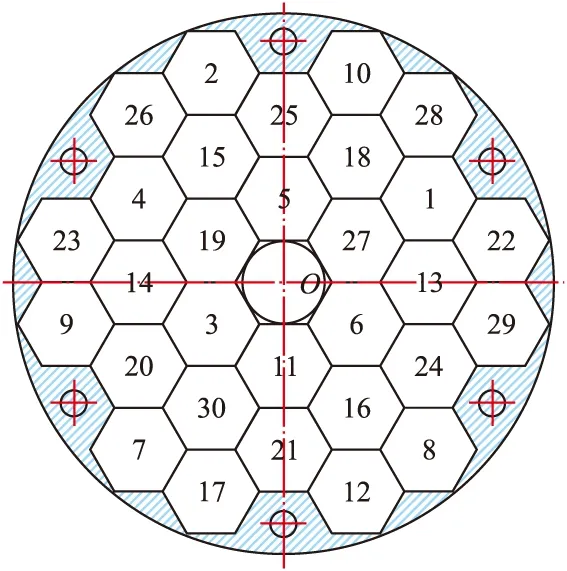
图9 第一层子弹优化后排布方式

3.2 不同层间子弹排布方式

子弹抛撒时,各层子弹在载弹舱中几乎同时被推出(两层子弹被推出载弹舱的间隔时间很小,可以忽略不计),则子弹经过空中自由落体落入水中后,各层子弹垂直方向距离很小,其空间距离主要取决于各层子弹间的水平距离。

上文中数据拟合所得的层间子弹水平距离最小值dmin与Δn的线性函数表达式为dmin=0.17+0.09 Δn,即母弹内相邻放置的两层子弹其空间距离最小值为0.26 m。其它各层子弹间空间距离最小值的计算方法与此类似。当n=7时,dmin=0.8 m。由于子弹最小正常工作间距为0.8 m。因此,认为装配入母弹后层数差大于等于7层的子弹起爆不会彼此造成影响。

对母弹内所有层数差小于等于6层的子弹层号进行排序,使得其起爆时间间隔增大。方案中暂定序号相邻的两枚子弹间的起爆时间间隔t1=0.5 s,则子弹序号相邻的两层子弹间的最小起爆时间间隔为t1=0.5 s(例如30号与31号子弹),子弹序号不相邻的两层子弹间最小起爆间隔为15.5 s(例如30号与61号子弹)。由于爆炸冲击时间极短,子弹引信电路受冲击后恢复正常状态所需时间也在1 s以内,故认为15.5 s后的爆炸冲击不会对其它子弹造成影响。因此仅需对子弹序号进行排列,使得母弹中层数差小于等于6层的子弹序号不相邻即可。满足该要求的排布方案有很多,在该问题上,这些排布方案对子弹的最终影响结果是等效的。随机选取一种满足上述要求的新排列方案,其与原方案的对比如表4所列。

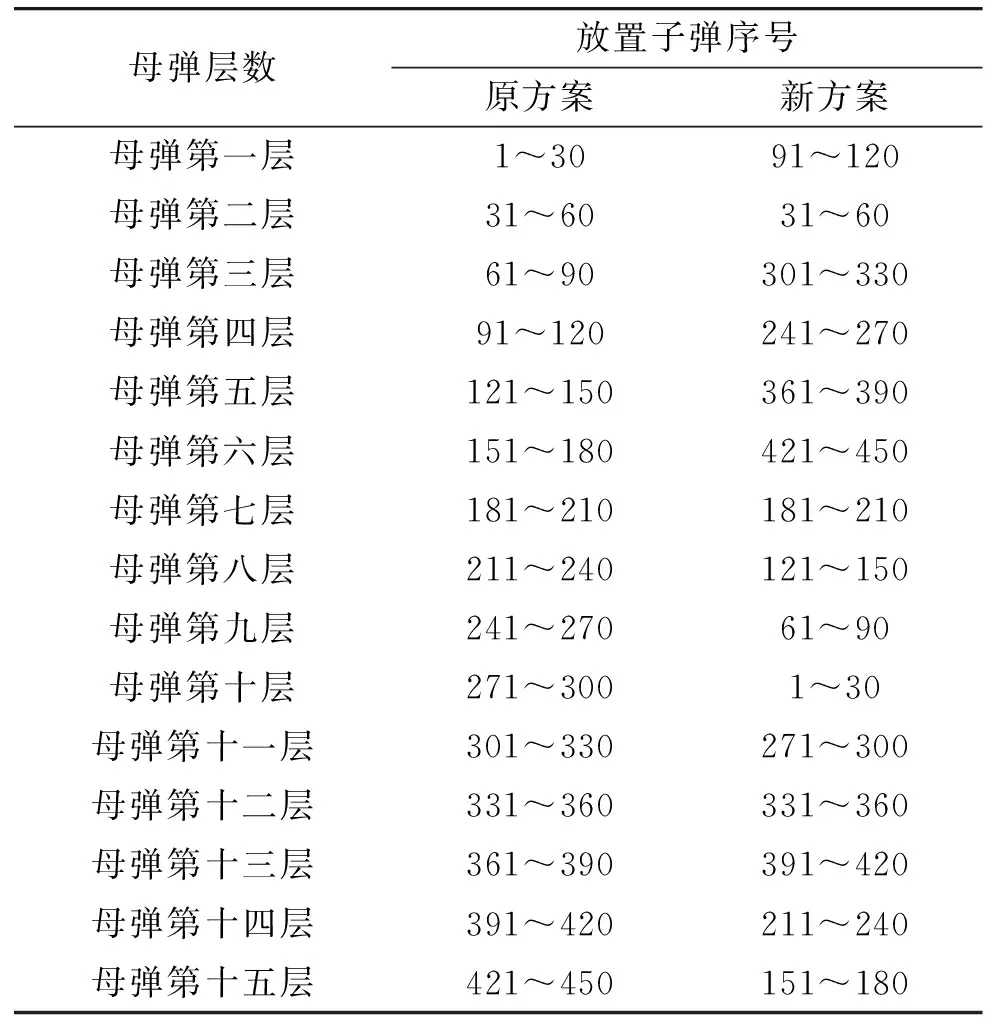
表4 不同层间子弹新排列方案与原方案对比

若考虑使得层数差小于等于7层的子弹序号不相邻,则可将序号相邻的两层子弹的最小空间距离再提高0.09 m。但由于子弹共有15层,对于第八层子弹而言,层数差小于等于7层即为所有层子弹,则必定存在子弹序号相邻的情况。因此,仿真所得方案已为最优解。

4 分析与讨论

4.1 同层内子弹排布结果分析

受水下爆炸冲击波的影响,子弹最小正常工作间距仅为0.8 m,而试验表明同一层内存在一定比例落点“重合”的子弹。考虑最不利的情况,假设同层内有3枚子弹抛撒后距离较近,按原方案,其中2枚子弹相距0.5 s起爆,意味着另一枚子弹在0.5 s内承受了2次爆炸冲击,冲击波叠加将对子弹造成更大危害;按新方案,2枚子弹相距2 s起爆,另一枚子弹受到冲击波的危害会远小于原方案。实际进行水下爆炸模拟试验时出现过爆炸瞬间电路短时断电和信号输出延时、出现延时后马上重新检测电路而电路又恢复正常的情况。若2次爆炸间隔时间由0.5 s增加到2 s,则可给电路恢复留出更多的缓冲时间,从而有利于降低失效率。另外,子弹质量较小,在第1枚子弹爆炸冲击波的作用下,另2枚子弹在水平方向会有远离的趋势,时间长则意味着其距离会更远,也能减小爆炸冲击对子弹的影响。总之,新排列方案有利于降低子弹抛撒后相互殉爆和因爆炸冲击引起机械结构或电路失效的可能性。

4.2 不同层间子弹排布结果分析

对于不同层间子弹,按原方案,根据拟合的层间子弹水平距离公式,第一层与第二层子弹的空间距离最小值为0.26 m,其中放置的子弹序号相邻,则其最小起爆时间间隔为0.5 s(如30号与31号子弹)。存在如下情况,即某一序号子弹(例如31号)在0.5 s内承受2次其它层子弹的近距离爆炸冲击(例如29号和30号),爆炸冲击波叠加可能对子弹造成更大危害;而按新方案,母弹中相邻两层子弹的序号不相邻,则与某一序号子弹相近的其余各层子弹与该枚子弹的起爆时间间隔至少为15.5 s,有利于减小爆炸冲击对该枚子弹的影响。另外,新方案可给电路恢复正常状态留出更多的缓冲时间(由0.5 s提高到15.5 s),从而有利于降低子弹引信电路失效率。

5 结束语

为了降低水声干扰子母弹水中序爆子弹抛撒后相互殉爆可能性,文中提出了母弹内同层子弹的时序优化排布方案和不同层间子弹的时序优化排布方案。同层内排布方案将相邻子弹间的起爆时间间隔最小值由0.5 s提高到2.0 s,不同层间排布方案使得母弹中层数差小于等于6层的子弹序号不相邻。新的子弹时序排布方案有利于降低子弹抛撒后相互殉爆和因爆炸冲击引起机械结构或电路失效的可能性,从而提高子弹正常工作概率。

[1] 孔维红, 姜春兰, 王在成. 某型航空子母弹子弹地面散布研究 [J]. 航空兵器, 2005(4): 43-46.

[2] 孙学武. 水声干扰弹子弹水下爆炸特性及抛撒动力学分析 [D]. 南京: 南京理工大学, 2011.

[3] 胡宏伟, 鲁忠宝, 郭炜, 等. 水中爆炸的殉爆试验方法 [J]. 爆破器材, 2014, 43(3): 25-28.

[4] 鲁忠宝, 胡宏伟, 刘锐, 等. 典型装药水下爆炸的殉爆规律研究 [J]. 鱼雷技术, 2014, 22(3): 230-235.

[5] 冯彦哲, 王雨时. 使母弹威力最大化的子母弹子弹横截面形状与布局分析 [J]. 弹箭与制导学报, 2008, 28(3): 135-142.

Arrangement Optimization of Submunition Initiated in Sequence to Reduce Possibility of Sympathetic Detonation after Dispersal

CAI Hongjie,WEN Quan,WANG Yushi,ZHANG Zhibiao

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Since short distance of submunition initiated in sequence under water may cause sympathetic detonation and affect its working ability, after analysis of data of a dispersal experiment, distance distribution of submunition was acquired. Specifically, mean value of distance of non-adjacent submunitions is greater than that of adjacent ones obviously, the greater the difference of tier number is, the greater distance of two submunitions is between two tiers. According to the conclusions above, better order arrangement of submunition in the same tier and among different tiers in cargo projectile was proposed. The new arrangement is beneficial to decrease the possibility of sympathetic detonation and damage of mechanical structure and circuit after dispersal, thus, increasing the probability of submunition working properly.

cargo projectile; Monte-Carlo method; design scheme; sequence arrangement optimizing; Weibull distribution

2015-07-23

蔡泓杰(1991-),男,江苏无锡人,硕士研究生,研究方向:引信及弹药总体技术。

TJ413.3

A