一种基于导航坐标系的巡飞弹航迹跟踪方法*

李怀涛,孙 静,刘大卫,夏群利

(1 北京理工大学宇航学院,北京 100081;2 中国兵器科学研究院,北京 100089)



一种基于导航坐标系的巡飞弹航迹跟踪方法*

李怀涛1,孙 静2,刘大卫2,夏群利1

(1 北京理工大学宇航学院,北京 100081;2 中国兵器科学研究院,北京 100089)

针对巡飞弹定高巡飞航迹跟踪的问题,提出了一种基于导航坐标系的航迹跟踪方法。将整条航路分为直线飞行和转弯飞行阶段,建立动态导航坐标系,分别利用直线控制策略和转弯控制策略,将航迹跟踪简化为在导航坐标系下修正横向侧偏距偏差的问题,省略航向角偏差控制,确保巡飞弹在飞行过程中沿着理想航线飞行。通过仿真证明,此方法使得巡飞弹实际飞行航迹偏离理想航迹的误差很小,达到良好的跟踪效果。

巡飞弹;航迹跟踪;导航坐标系;侧向偏差

0 引言

巡飞弹是集多种功能于一身的智能化和信息化新概念武器[1-2],是今后武器弹药领域的一个重要发展方向。巡飞弹的主要任务是去目标区域上空进行“巡弋飞行”,实现侦察与毁伤评估、精确打击、通信中继等功能[3-4]。在执行作战任务时,需要预先对巡飞弹的航路进行规划,并要求巡飞弹对规划出的航迹进行准确跟踪,实现对任务区域的精确、全面覆盖。规划出的任务曲线通常比较复杂,变化较大[5],战场环境和态势复杂多变,要求航迹跟踪具有较高的实时性。因此,需要研究一种新的简单易行的导航算法,在减轻弹上计算机压力的同时,提高巡飞弹在复杂环境下的航迹跟踪能力。文中针对巡飞弹航迹跟踪问题提出了一种基于导航坐标系的航迹跟踪方法,解决了巡飞弹不能严格按照预设航迹飞行的问题,并通过数字仿真证明了此方法的有效性。

1 航迹跟踪方法基本思想

巡飞弹航迹跟踪的概念是:规划出航迹点并装订入弹载计算机,航迹由一系列航路点和相邻航路点相连接的直线段组成,航迹点包含由经度、纬度、高度或直角坐标表示的位置信息;利用弹上组合导航装置测量导弹实时位置,弹载计算机将巡飞弹实际位置和理想航迹点进行比较得到弹道偏差,通过控制系统对弹道偏差进行修正,使巡飞弹实际飞行航迹与理想航迹一致。

在巡飞弹飞行过程中,主要包括爬升、俯冲、直飞、转弯等飞行状态[6]。其中,定高巡飞是最主要的飞行阶段,文中重点研究这一阶段的巡飞弹航迹跟踪策略。

文中采用的航迹跟踪方法的基本思想是:基于动态导航坐标系,将巡飞弹定高巡飞分解为直线和转弯飞行两种形式,分别提出了直线控制和转弯控制方法,使巡飞弹在飞行过程中时刻沿着理想航迹飞行。

2 航迹跟踪方案设计

此方案是基于巡飞弹飞行高度保持不变的假设条件下来进行的,因此省略俯仰通道的控制方案,仅考虑巡飞弹水平面内航迹跟踪问题。

2.1 动态导航坐标系

航迹跟踪方案的关键是建立动态导航坐标系,建立过程如图1所示。OXZ为惯性坐标系,与地球固连,随地球自转而旋转,这里以巡飞弹为研究对象认为地球静止不动;设巡飞弹飞离的航路点为Ai,定义平面直角坐标系OgXgZg为导航坐标系,以航路点Ai为坐标原点,以下一个航路点与原点的连线为OgXg轴,方向指向下一个航路点为正,OgZg轴与OgXg轴垂直,沿着OgXg方向左手边为正。

导航坐标系与惯性坐标系的变换关系为:

(1)

ΔXi=Xni-X0iΔZi=Zni-Z0i

(2)

其中:ψ为偏航角;X0i、Z0i为导航坐标系原点在惯性系下的坐标值;Xni、Zni为惯性系下巡飞弹的当前位置的坐标值;ΔXi、ΔZi为坐标值的差;Xg、Zg为巡飞弹在导航坐标系下的坐标值。

在巡飞弹完成整个转弯过程前,以当前导航坐标系作为制导指令生成参考坐标系。当巡飞弹进入下一个直线航路飞行过程时,新的导航坐标系随之建立。

通过坐标变换可以得到巡飞弹任意时刻在导航坐标系下的坐标值,于是就将航迹跟踪问题简化为在导航坐标系下修正横向侧偏距偏差的问题,而不用考虑巡飞弹的航向偏差,减小了计算量,而且实时性和快速性更好。

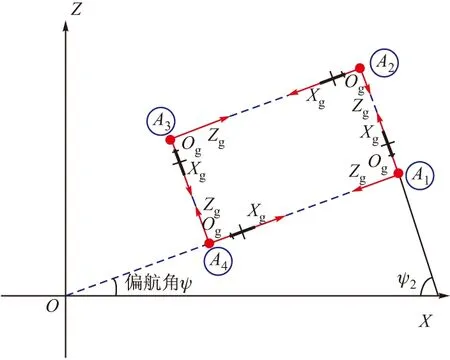
图1 动态导航坐标系示意图

2.2 直线飞行阶段跟踪方法

巡飞弹直线飞行阶段采用直线航迹跟踪方法,通过修正当前航点与导航坐标Xg轴的侧向偏差进行导引控制,控制指令生成如图2所示。

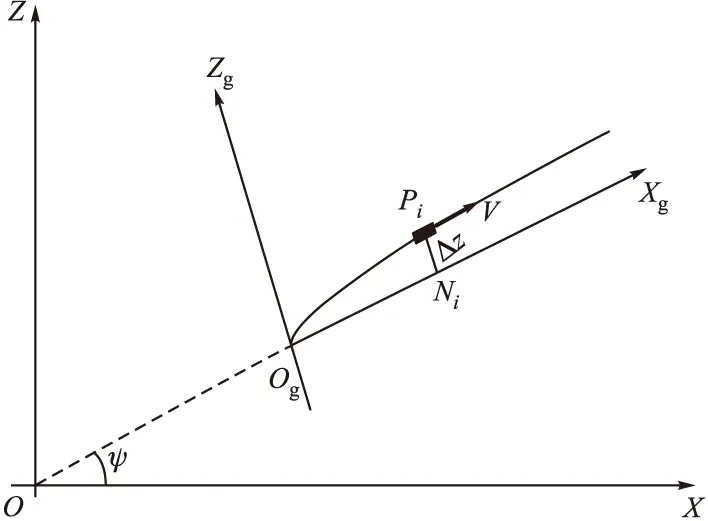
图2 巡飞水平面内几何示意图

其中,导航坐标系的Xg轴应为巡飞弹理想航路;Pi为巡飞弹实际位置点;Ni为巡飞弹理想航迹点位置。可得侧向偏差量:

Δz=PiNi

(3)

Δz的值可由下面方法获得:

规划航路点的坐标都是已知的,由此可得出相邻两航路点间的直线方程:

Ax+By+C=0

(4)

当前点在导航坐标系下的坐标Pi(xi,yi)可根据组合导航位置信息和坐标变换公式求得,距离偏差Δz可由点到直线的距离公式得出:

(5)

通过控制Δz来减小距离的侧向偏差量,将Δz作为偏航通道制导指令,然后按照一定的控制策略,根据BTT算法,计算滚转角指令,通过控制滚转角,保持侧滑角为零,使巡飞弹产生航向改变从而按照预定航迹直线飞行。

2.3 转弯飞行阶段跟踪方法

因为误差的存在,巡飞弹在进行转弯时需要通过转弯控制方法。在航路转弯阶段,采用提前转弯的方案,制导指令形成计算如图3所示。

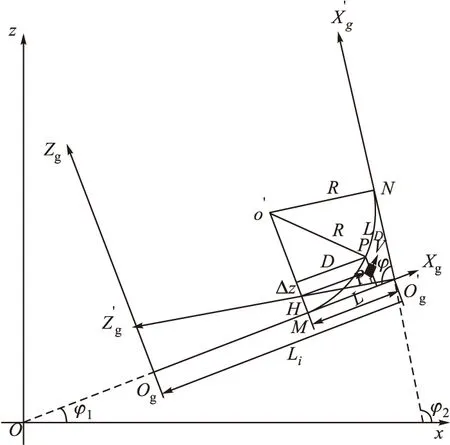
图3 巡飞弹转弯示意图

图中:Pi为巡飞弹当前实际位置;P为巡飞弹理想航迹位置;M为转弯进入点;N为转弯结束点;R为转弯半径;L0为理想转弯路径;L为转弯的提前量;φ为转弯夹角;ψ1、ψ2分别为相邻两段直线航路的偏航角;D为由巡飞弹当前点到转弯进入点的距离,可由当前点与转弯进入点在导航坐标系下的Xg轴坐标差值解得;H为巡飞弹当前实际位置到预设航路的直线距离,可通过式(5)求得。

转弯的提前量L由转弯夹角φ和转弯半径R确定。其中,转弯夹角φ可由相邻两直线航路的偏航角关系计算得出;转弯半径R受侧向可用过载的限制,可根据巡飞弹允许的侧向机动能力来选定。

根据图3中关系可以得出:

转弯夹角:

φ=ψ1-ψ2+180°

(6)

转弯提前量:

L=R/tan(φ/2)

(7)

侧向偏差量:

(8)

转弯阶段航迹跟踪以Δz为制导指令,通过修正侧向偏差量Δz的值,不断调整偏航制导指令以保证转弯半径不变,完成巡飞弹的转弯。当巡飞弹飞抵转弯结束点N处时,标志着本次转弯过程结束,开始进入下一段航路的直线飞行阶段,同时切换成直线飞行控制方案。

将巡飞弹航路分解成直线飞行和转弯飞行两个阶段,通过计算两个阶段的侧向距离偏差生成偏航制导指令(俯仰制导指令由高度控制策略生成,这里不作重点讨论),采用BTT即倾斜转弯控制方式实现了航迹跟踪。

3 数字仿真

下面通过数学仿真来验证巡飞弹航迹跟踪方案设计的可行性。

仿真条件为:巡飞弹质量50 kg,飞行高度500 m,飞行速度110 m/s,航路点个数为6个,坐标分别如下:(0,0),(0,-20 000),(10 000,-20 000),(10 000,-10 000),(-10 000,-10 000),(-10 000,-15 000)。仿真历行时间560 s,经过5个直线飞行阶段和4个转弯飞行阶段。仿真结果如图4所示。

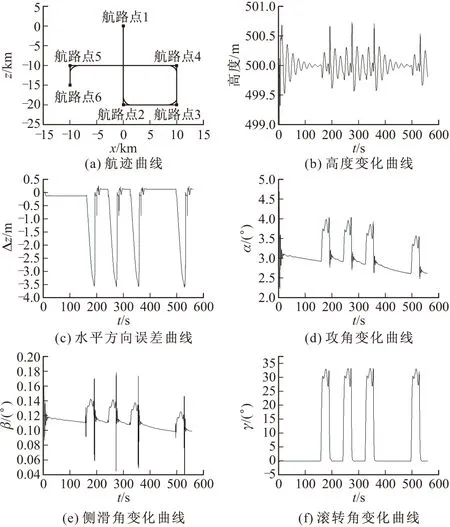
图4 仿真结果

通过仿真结果图4(a)可以看出(图中虚线表示规划航迹,实线表示实际飞行航迹),巡飞弹在整个飞行过程中能够沿预设航迹飞行。由图4(b)和图4(c)知,只有在转弯飞行阶段水平方向偏差和高度偏差较大(Δz<3.5 m,Δh<0.8 m),在直线飞行阶段偏差很小(Δz<0.25 m,Δh<0.3 m)。

由图4(d)可知,在整个飞行过程中攻角都比较小,不超过4°,符合巡飞弹大展弦比气动结构特性;图4(e)为巡飞弹侧滑角变化曲线,可见侧滑角的值基本保持为零;图4(f)表示弹体滚转角的变化,可以看出,在转弯过程中巡飞弹处于大滚转角飞行状态,最大值约为35°。这里正是采用BTT控制策略,抑制侧滑角,通过滚转控制弹体转弯的结果。

仿真结果表明,采用上述航迹跟踪方法,巡飞弹能够达到准确跟踪理想航迹的目的,具有很好的跟踪效果。

4 结论

在巡飞弹航迹跟踪问题中引入了导航坐标系,省去了对巡飞弹任意时刻偏航角度信息需求的麻烦,减轻了计算压力,算法简单易行,具有更强的实时性。将巡飞弹航迹跟踪问题分解为直线跟踪和转弯跟踪,采用修正侧向偏差的方法,能够控制巡飞弹f按照预定航路飞行。从仿真结果可以看出,在整个飞行过程中航迹跟踪偏差极小,该方法可行,具有广阔的工程应用前景。

[1] 李佳, 王昊宇, 房玉军. 侦察巡飞弹发展及关键技术分析 [J]. 飞航导弹, 2015(2): 16-20.

[2] 解广华, 邹丹. 巡飞弹发展看点 [J]. 轻兵器, 2014(21): 10-13.

[3] 高晓敏. 新概念信息化弹药的现状与发展 [J]. 四川兵工学报, 2008, 29(4): 69-73.

[4] 郭美芳, 彭翠枝. 巡飞弹: 一种游弋待机的新型弹药 [J]. 现代军事, 2006(4): 49-52.

[5] 崔生旺, 刘莉. BTT导弹航迹跟踪技术 [J]. 弹道学报, 2007, 19(1): 17-20.

[6] 黄叙磊, 王根, 张宝. 巡飞弹航迹导引方法研究 [J]. 弹箭与制导学报, 2010, 30(2): 45-48.

A Trajectory Tracking Approach Based on Navigation Coordinates for Loitering Munition

LI Huaitao1,SUN Jing2,LIU Dawei2,XIA Qunli1

(1 School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2 China Research and Development Academy of Machinery Equipment, Beijing 100089, China)

To solve the problem of trajectory tracking for loitering munition at constant height, a trajectory tracking approach based on navigation coordinates for loitering munition was put forward. Based on navigation coordinate, omitting azimuth deviation control, two different control strategies were applied to correct lateral deviation in order to ensure the loitering munition flying along ideal trajectory after the whole trajectory was divided into straight line stage and wheeling stage. The simulation result shows that the approach can make sure that during munition flying, the error of deviation from ideal track is quite small and the tacking effect is good.

loitering munition; trajectory tracking; navigation coordinates; lateral deviation

2015-06-23

李怀涛(1988-),男,天津宝坻人,硕士研究生,研究方向:飞行器总体设计、飞行器制导与控制。

TJ765.3

A