掌握基本知识轻松解决问题

韩俊元

掌握基本知识轻松解决问题

韩俊元

中考中经常会涉及“平面图形的认识（一）”中的问题，这些问题难度不大，我们只有掌握好基本知识，就能迅速准确解决.

一、有关“角”的问题

例1（2013·江苏淮安）如图1，三角板的直角顶点在直线l上，若∠1=40°，则∠2的度数是______.

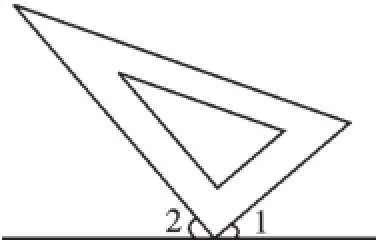
图1

【分析】由三角板的直角顶点在直线l上，根据平角的定义可知∠1与∠2互余，又∠1=40°，即可求得∠2的度数.

【解答】如图，三角板的直角顶点在直线l上，则∠1+∠2=180°-90°=90°.

∵∠1=40°，∴∠2=50°.

故答案为50°.

【点评】本题只要理解平角、互余的定义即可解决问题，是基础题，熟记互为余角的两个角的和等于90°是解题的关键.

例2（2013·浙江湖州）把15°30′化成度的形式，则15°30′＝____度.

【分析】15°30′=15°+（30÷60）°=15.5°，故填15.5.

【点评】本题考查了角的单位：度、分、秒的换算.由高级单位变成低级单位乘进率，由低级单位变成高级单位除以进率.

例3（2014·福建泉州）如图2，直线AB与CD相交于点O，∠AOD=50°，则∠BOC= ______°.

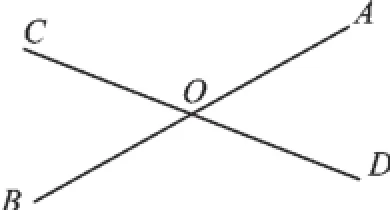
图2

【分析】根据对顶角相等，可得答案.

【解答】∵∠BOC与∠AOD是对顶角，∴∠BOC=∠AOD=50°，故答案为50.

【点评】本题考查了对顶角与邻补角，对顶角相等是解题关键.

例4如图3，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB=40°，∠COE=60°，则∠BOD的度数为（）.

A.50°B.60°C.65°D.70°

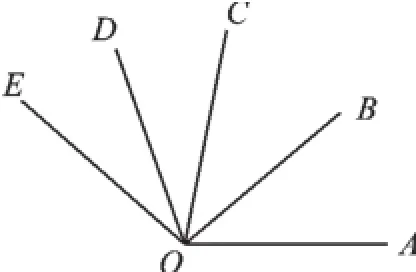
图3

【分析】先根据OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB=40°，∠COE=60°，求出∠BOC与∠COD的度数，再根据∠BOD=∠BOC+∠COD即可得出结论.

【解答】∵OB是∠AOC的角平分线，OD是∠COE的角平分线，∠AOB=40°，∠COE=60°，

∴∠BOD=∠BOC+∠COD=40°+30°= 70°.

故选D.

【点评】本题考查的是角的计算，熟知角平分线的定义是解答此题的关键.

二、有关“线”的问题

例5（2013·湖北武汉）两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，…，那么六条直线最多有（）.

A.21个交点B.18个交点C.15个交点D.10个交点

【解答】C.

【点评】本题属于找规律的问题，它建立在直线与直线的交点的个数变化之上，我们应该从特殊情形考虑，进而总结归纳出规律.

例6（2014·山东济宁）把一条弯曲的公路改成直道，可以缩短路程.用几何知识解释其道理正确的是（）.

A.两点确定一条直线

B.垂线段最短

C.两点之间线段最短

D.三角形两边之和大于第三边

【分析】此题为数学知识的应用，由题意把一条弯曲的公路改成直道，肯定要尽量缩短两地之间的路程，这就用到两点间线段最短定理.

【解答】要想缩短两地之间的路程，就尽量使两地在一条直线上，因为两点间线段最短.故选C.

【点评】本题考查了线段的性质，牢记线段的性质是解题关键.

三、综合型问题

例7如图4，已知∠AOB是直角，OE平分∠AOC，OF平分∠BOC.

（1）若∠BOC=60°，求∠EOF的度数；

（2）若∠AOC＝x°（x＞90），此时能否求出∠EOF的大小？若能，请求出它的数值；若不能，请用含x的代数式来表示.

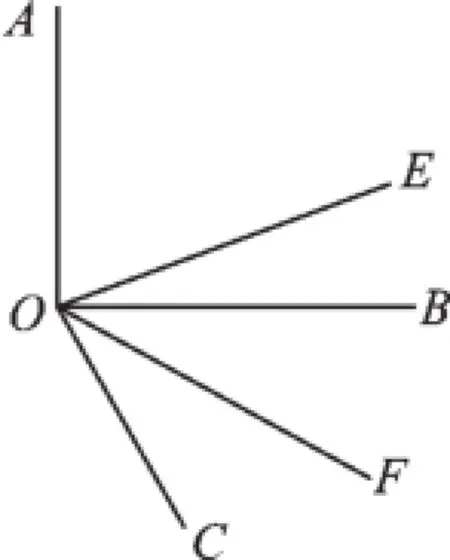
图4

【分析】解决本题首先要抓住∠EOF=∠COE-∠COF，对于第（1）问，直接求出∠COE、∠COF这两个角即可，而第（2）问，则要设∠AOC=x°，然后用x表示出∠COE、∠COF这两个角即可.

【解答】（1）因为∠AOB=90°，∠BOC= 60°，所以∠AOC=150°.

又因为OE平分∠AOC，所以∠COE= 75°.

又OF平分∠BOC，所以∠COF＝30°.

所以∠EOF=∠COE-∠COF=45°.

（2）因为∠AOC=x°（x＞90），且OE平分∠AOC，

【点评】紧紧抓住角的和差表示，结合角平分线的定义，运用从特殊到一般的思想方法，问题则会化难为易.

例8如图5，已知数轴上点A表示的数为8，B是数轴上在A点左边的一点，且AB= 14.动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒.

图5

（1）写出数轴上点B表示的数______；点P表示的数_____（用含t的代数式表示）；

（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？

（3）若M为AP的中点，N为PB的中点，点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长.

【分析】（1）根据已知可得B点表示的数为8-14；点P表示的数为8-5t；

（2）点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，根据AC-BC=AB，列出方程求解即可；

（3）分①当点P在A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差求出MN的长即可.

【解答】（1）∵点A表示的数为8，B在A点左边，AB=14，

∴点B表示的数是8-14=-6，

∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，

∴点P表示的数是8-5t.

故答案为：-6，8-5t.

（2）设点P运动x秒时，在点C处追上点Q，则AC=5x，BC=3x，

图6

∵AC-BC=AB，

∴5x-3x=14，解得：x=7，

∴点P运动7秒时追上点Q.

（3）线段MN的长度不发生变化，都等于7，理由如下：

∵①当点P在A、B两点之间运动时：

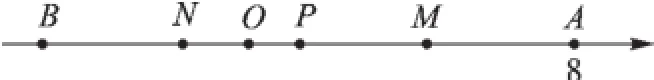
图7

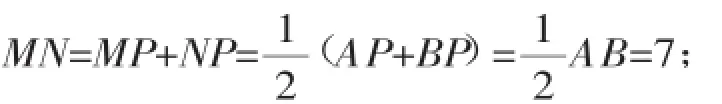
②当点P运动到点B的左侧时：

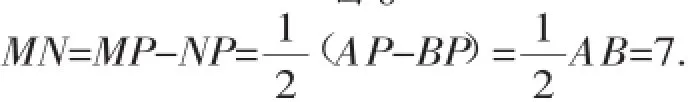
图8

【点评】本题属于一道综合题，不仅用到了线段的知识，还结合了数轴、方程、两点之间的距离等相关知识，同时还运用了初中阶段经常遇到的一种数学思想方法——分类讨论.

（作者单位：江苏省盐城市初级中学）