基于层次分析法和灰色关联度分析的高校教师教学质量评价研究*

陈 静

(商丘学院 工商管理学院，河南 商丘 476000)



基于层次分析法和灰色关联度分析的高校教师教学质量评价研究*

陈 静

(商丘学院 工商管理学院，河南 商丘 476000)

针对高校对教师教学质量的评价和考核不够客观，督导部门进行评教难度较大，教师的教学成果难以细化和量化等问题，提出了比较全面的评价指标体系。运用层次分析法确定各个指标所占权重值，以灰色关联分析法确立评价准则，进而建立教师教学质量评价模型。通过实例验证，教师可根据得出的教学评价结果分析自己在同行之间的排名情况，同时可以找出自身存在的优点和不足之处，对于提升高校教育教学质量起着重要的作用。

层次分析法；灰色关联度；教学质量；评价指标

0 引言

教学评价活动从20世纪80年代开始在我国各大高校受到重视，同时也成为高校督导管理和教学管理部门对教师进行教学管理的重要依据。教师的教学评价效果也是衡量教师教学质量的重要组成部分。由于对教师的教学评价工作量大且涉及到的教师数量较多，其重要性不容忽视。目前，国内关于运用层次分析法和灰色关联分析法构建评价模型的研究成果包括：杨红娟、夏莹、王青云[1]通过运用层次分析法和灰色关联度分析法对

昆明理工大学两位教师进行了教学效果评价。通过对两位教师的教学效果评价得分情况进行分析，得出各自在教学过程中的优势和存在的不足之处，进而在提高教师的教育教学水平方面起到一定的促进作用。卢康[2]结合层次分析法和灰色关联分析法从实习员工的工作表现和行为表现2个一级指标、12个二级指标进行评价，通过实习员工的绩效考核得分情况作出对实习员工去留的决策，在企业的用人机制方面起到一定的辅助作用。阮家港[3]运用因子分析和聚类分析构建的评价模型对商丘学院20位青年教师的教育教学质量进行评价分析，使得学院教学督导部门的评价结果更加客观和公正。王云鹏、丁荣良[4]运用灰色关联度分析法从供应商提供的产品质量、产品价格、售后服务、供应能力等九个方面对供应商进行评价，为企业进行供应商的选择提供一定的参考依据，从而使企业可以选择满意度较高的供应商。

通过运用层次分析法和灰色关联分析法构建模型的基础上，以M学校的青年教师为例，从教学态度、教学内容、教学方法和手段、教学效果四个方面对教师进行教育教学质量的评价，在一定程度上可以提高教师自身的教育教学水平，同时也可为教学督导和教学管理提供一定的决策依据。

1 层次分析法和灰色关联分析法的相关理论基础

1.1 层次分析法

层次分析法(Analytic Hierarchy Process，简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法通过两两比较确定各个因素对教学质量的影响程度，然后综合专家的打分，对指标的重要性依次进行科学合理的排序。层次分析法的步骤[5]为：

1.建立评价结构

层次分析法的层次是由最高层的目标层到中间的准则层再到最下层的方案层，按照从上到下的顺序将结构划分为三大层，其中目标层一般只有一个元素，是最终要达到的目标，也是层次分析法所要达到的目的，准则层是目标层的分解目标，隶属于目标层，方案层是为了达到对应的准则层的目标而采取的具体方案，下层的要素都隶属于其上层要素，并且最终都是为了要达到目标层的目的。

2.构造判断矩阵

对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较，构造两两比较判断矩阵，并进行一致性检验。以上述的递阶层次为基础，通过对同一层次的指标进行两两比较确定判断矩阵。设目标层A的下层有n个指标，分别为x1,x2,…,xn,其中i，j=1,2，…，以aij表示要素i与要素j相比的重要性程度。判断矩阵的标度定义如表2所示。根据两两要素重要程度比较，得出n个要素关于A的判断矩阵：

3.层次结构单排序以及满意一致性检验

构造判断矩阵A之后，即可求出其最大特征值λmax，再利用公式AW=λmaxW求解出特征向量W，将特征向量W归一化处理，即可求出同一层次的各要素相对于上一层所对应的要素的重要性权值。把上一层各要素作为下层要素比较的依据，可以做出下层的判断矩阵，然后计算出下层要素相对上层要素的权重值。

对矩阵A进行一致性检验的基本思路是：矩阵A的最大特征根λmax与n越接近，则越能通过一致性检验。通常情况下，使用一致性比率C.R.来检验矩阵的一致性，当C.R.<0.1时，则说判断矩阵A有满意一致性，接受该分析结果；否则，则说判断矩阵不具有满意一致性，需要对矩阵进行修改。CR=CI/RI, C.R.为一致性指标，C.I.=(λmax-n)/(n-1)，n为矩阵阶数；R.I.为平均随机一致性指标。

4.层次总排序及一致性检验

上一阶层A包含m个元素，分别为A1,A2,…,Am，对应的权重分别为a1,a2,…,am，层A的下层B包含n个元素B1,B2,…,Bn，关于i的层次排序权重分别为j。利用权重合成法求B层各要素的层次总排序权重为b1,b2,…,bn，即i，i=1，2，=1,2，n。对层次总排序的权重向量进行一致性检验，先使得第k-1层的第j个要素为准则的一致性指标为n，平均随机一致性指标为j(j=1,2，…，=1,2)，那么第k层的综合指标分别为：

m

同层次单排序一样，当i<0.1，则说明第k层以上的判断都具有满意一致性，接受分析结果；反之，则需要进行修正。通常情况下，单层次排序检验具备满意一致性，则不需要再对整体进行满意一致性检验。

1.2 灰色关联分析法

灰色关联分析是灰色系统理论的重要组成部分，该方法通过分析得出影响教师教学质量的四个因素之间的关联系数，进而求出每位教师的得分情况，通过得分情况对五位教师的教学质量进行排序。灰色关联分析的计算步骤[2]如下：

第1步：确定参考数列和比较数列

选择一个参考数据列 x0，x0=(x01，x02，…x0n)。有 m个比较数列 x1，x2，xm，xi=(xi1，xi2，xi3…，xin)(i=1，2，3…，m) ，参考数据列 x0的元素是企业内部实习岗位最优秀或是企业的目标指标中选取值。比较数列 xi中，xi1，xi2，…xin为被评价指标中各指标值。

第2步：变量序列标准化

第3步：计算关联系数

(1)根据公式△i(k)=|x'0(k)-x'1(k)|△i=|△i(1)，△i(2)，…，△i(n),i=1,2,m|，求差序 ；

1.3 计算灰色加权关联度

2 实例分析

以M学校的5名青年教师T1、T2、T3、T4、T5为例进行实证分析。运用层次分析法和灰色关联分析法对5位教师的教学质量进行评价分析，根据评价情况分析各位教师的优点和不足，进而为青年教师提升自身教育教学水平提供一定的参考依据。

2.1 确定评价教师教学质量的评价指标体系

根据M高校原有的教学质量评价指标体系，结合其他学者的研究以及M学校自身的特点和青年教师的自身的实际情况，构造如表1所示的评价指标体系。

表1 M学校教师教学质量评价指标体系

2.2 构建判断矩阵和进行一致性检验

根据相关文献进行综合分析的基础上，并运用专家评分法，对目标层和准则层进行判断矩阵的赋值和一致性检验，如表2至表6所示。

表2 目标层M学校教学质量评价指标体系的判断矩阵及一致性检验

注：lmax=4.0137； CI=0.0046； RI=0.9； CR=0.0051

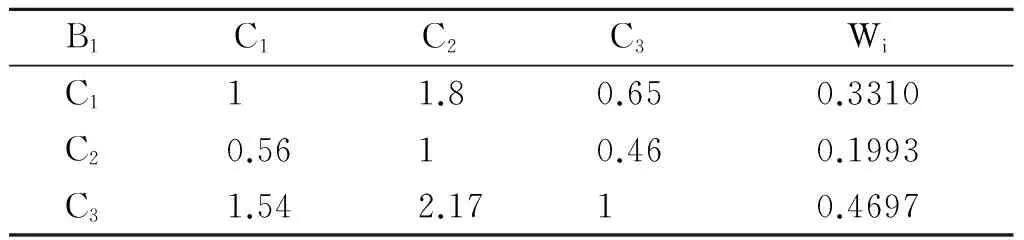
表3 准则层教学态度的判断矩阵及一致性检验

注：lmax=3.0065； CI=0.0033； RI=0.58； CR=0.0056

表4 准则层教学内容的判断矩阵及一致性检验

注：lmax=3.0067； CI=0.0033； RI=0.58； CR=0.0058

表5 准则层教学方法和手段的判断矩阵及一致性检验

注：lmax=2； CI=0； RI=1E-6； CR=0

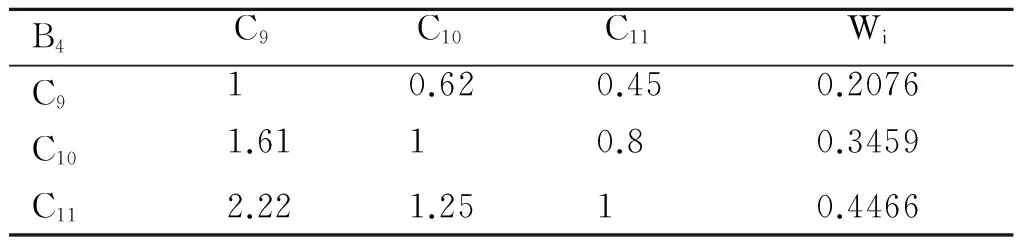
表6 准则层教学效果的判断矩阵及一致性检验

注：lmax=3.0011； CI=0.0005； RI=0.58； CR=0.0009

从表格中计算数据可知，目标层和准则层的赋值都通过了一致性检验，说明赋值是有效的。表中的数据说明教学态度、教学内容、教学方法和手段、教学效果相对于任课教师的教学质量的重要程度分别是0.1855，0.2659，0.2059，0.3426。

2.3 计算各个指标所占权重

根据层次分析法求出的4个一级指标和11个二级指标所占的权重，求出各个指标所占指标的总权重(如表7所示)。

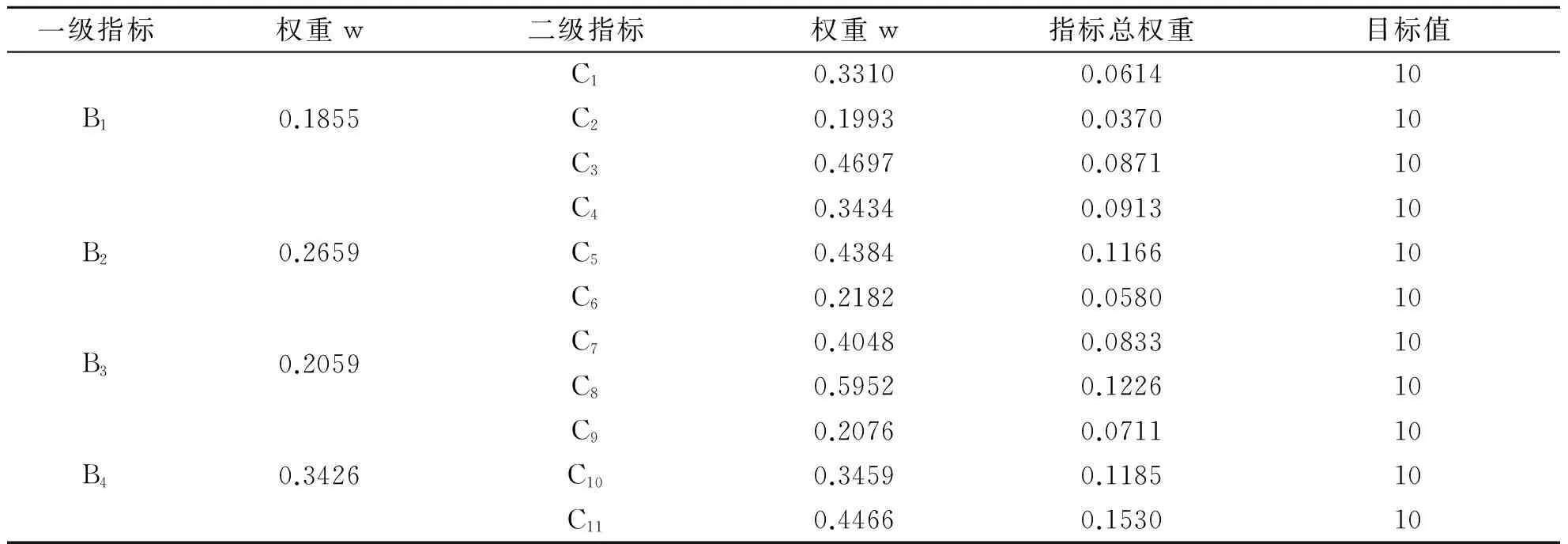
表7 M学校教学质量评价指标体系所占权重

2.4 根据学校教学督导组领导

分院领导，同事和学生组成的教学评价体系，对5位任课教师进行打分,计算每位教师各评价指标得分的平均值(每个指标满分10分)，5位教师的得分如表8所示。

表8 五位教师所得分数

2.5 确定参考序列和比较序列

参考序列X0=(10,10，10，10，10，10，10,10，10，10，10)

T1教师比较序列X1=(8.8，9.3，9.5，9.8，9.4，9.2，9.4，8.6，8.7，9.0，9.8)

T2教师比较序列X2=(9.4，9.7，9.6，9.1，9.2，9.3，9.2，9.6，9.0，9.2，9.2)

T3教师比较序列X3=(8.6，8.9，9.4，8.5，8.4，9.0，9.3，9.8，8.6，8.5，9.9)

T4教师比较序列X4=(9.0，9.2，9.5，9.4，8.6，9.0，9.2，8.6，9.0，8.8，9.4)

T5教师比较序列X5=(9.0，8.5，7.7，8.2，7.5，8.1，7.8，7.6，8.0，7.9，7.2)

2.6 对评价数据进行标准化处理

为了确保各个评价指标的度量标准一致，使得各个数据之间的运算关系更加科学合理，需要对指标数据进行标准化处理，将其化为[0,1]之间的数，需要对数据进行无量纲化。

2.7 求M学校五位教师的教学质量评价关联系数

(1)根据公式，求差序△i(k)=|x'0(k)-x'1(k)|△i=|△i(1)，△i(2)，…，△i(n),i=1,2,m|

Δ01=(0.12，0.07，0.05，0.02，0.06，0.08，0.06，0.14，0.13， 0.,1，0.02)

Δ02=(0.06，0.03，0.04，0.09，0.08，0.07，0.08，0.04，0.1，0.08，0.08)

Δ03=(0.14，0.11，0.06，0.15，0.16，0.1，0.07，0.02，0.14，0.15，0.01)

Δ04=(0.1，0.08，0.05，0.06，0.14，0.1，0.08，0.14，0.1，0.12，0.06)

Δ05=(0.1，0.15，0.23，0.18，0.25，0.19，0.22，0.24，0.2，0.21，0.28)

M=maxmaxΔ01(k)=0.14，m=minminΔ01(k)=0.02

M=maxmaxΔ02(k)=0.1， m=minminΔ02(k)=0.03

M=maxmaxΔ03(k)=0.16， m=minminΔ03(k)=0.01

M=maxmaxΔ04(k)=0.14， m=minminΔ04(k)=0.05

M=maxmaxΔ05(k)=0.28， m=minminΔ05(k)=0.1

(4)根据求得的灰色关联系数乘以各个二级指标所占的权重，计算五位教师的教学质量指标中的一级指标的得分情况，进而根据各一级指标所占的权重和乘以一级指标得分求出五位教师的总得分情况(如表10和表11所示)。

表9 各个二级指标的灰色关联系数

表10 M学校五位教师的教学质量评价一级指标得分

表11 M学校五位教师的教学质量评价总得分

3 结果分析

通过层次分析法对一级指标和二级指标进行权重的计算，使得各个指标所占权重更加科学合理；根据层次分析法所得权重进行灰色关联度分析，进而得出五位教师所得总分；进而可以清晰地看出各位教师存在的优点和不足之处。首先，根据教学效果评价总得分可以得出，五位教师的总分排名顺序为教师T4>教师T2>教师T1>教师T5>教师T3。其次，根据一级指标得分情况可以看出，教师T1在教学内容的安排和组织方面做得是比较好的，教师T3在教学方法的使用和教学手段的选择方面是略优于其他教师的。教师T4虽然是五位教师中总分数最高的，但是相比较而言，教师T4在教学方法和手段的选用方面还是略有不足的。最后，根据各个指标的结果，每位教师可以看出相比较其他同事而言，在教学评价方面自身的优势和劣势，为以后的教学质量提高提供一定的参考依据，同时也为教学管理人员对教师可以有针对性地进行监督，管理，从而为提高整个学校的教育教学质量提供一定的保障。

[1]杨红娟,夏莹,王青云.基于灰色关联度的高教效果评价—以《管理学》为例[J].价值工程，2015(1):245-247.

[2]卢康.基于层次分析法和灰色关联分析的实习员工绩效评估研究[J].科技与管理，2009,11(1):126-129.

[3]阮家港.基于因子-聚类分析的民办本科高校青年教师教学质量评价研究[J].数学的实践与认识,2015，45(4):86-93.

[4]王云鹏,丁荣良.运用灰色关联分析供应商的选择[J].管理纵横,2015(4):128-129.

[5]杜栋,庞庆华,吴炎.现代综合评价方法与案例精选[M].北京:清华大学出版社,2004:13-21.

[6]刘思峰,党耀国,方志庚，等.灰色系统理论及其应用[M].北京:科学出版社,2010:62.

Research on Teaching Quality of Teachers in Colleges Based on Factor Analysis and Degree of Grey Incidence

CHEN Jing

(School of Business Administration,Shangqiu University,Shangqiu 476000,China)

Based on the design of evaluation system in colleges, it is difficult to evaluate and check the teaching quality. Supervision departments have greater difficulty in evaluating teaching and teachers’ teaching achievements are difficult to refine and quantify. This paper establishes teaching quality evaluation model by using Analytical Hierarchy Process to determine the weighting of each index value and the gray correlation analysis method to establish evaluation criteria. Through the empirical analysis on the results of teaching, teachers can analyze their ranking in the colleagues and find out their advantages and disadvantages, thus it can play an important role in enhancing teaching quality in colleges.

analytical hierarchy process;degree of grey incidence; teaching quality; evaluation index

2015-12-25

陈 静(1982-)，女，河南商丘人，讲师、硕士。主要研究方向：企业管理。

G642；C93-4

A

1673-6125(2016)01-0022-06