基于旋转水槽试验的泥石流阻力坡降速率效应研究*
2016-12-19邓检良沈水龙
邓检良 余 斌 沈水龙
DENG Jianliang①② YU Bin② SHEN Shuilong①
基于旋转水槽试验的泥石流阻力坡降速率效应研究*
邓检良①②余 斌②沈水龙①

使用自主研发的旋转水槽制作稳定循环流动的泥石流,通过实测泥石流阻力坡降和流动速度,探索泥石流阻力坡降的速率效应。在旋转水槽试验中,通过控制线速度v,制作出稳定循环运动的泥石流,其阻力坡降J等于槽底坡降tanθ,可以实测。试验再现了野外的泥石流运动特性,观察到“龙头”、颗粒弹跳、低阻力坡降、固液相分离、剪切速率效应等现象。试验结果表明,在一定的流动速度范围内(例如试验中1.88m·s-1≥v>0.47m·s-1),泥石流的流动速度越高,阻力坡降越大; 如果泥石流运动速率过低(例如试验中v<0.47m·s-1),泥石流会出现固液两相分离现象,砾石(粒径>2mm)运动明显落后于液相运动。本项目的试验研究成果为泥石流制作和阻力坡降测量提供新途径,为泥石流阻力坡降的速率效应理论研究提供实验支持。
泥石流 阻力坡降 流动速率 旋转水槽试验
DENG Jianliang①②YU Bin②SHEN Shuilong①

0 引 言
在泥石流运动问题中,运动阻力是泥石流灾害防治中的关键参数之一,也是泥石流运动研究中最主要的问题之一(崔鹏等, 1993),理论计算方法尚无定论。目前大多数的泥石流的阻力理论研究是通过对泥石流体内部作用力的研究,计算不同条件下泥石流的阻力。由于泥石流由固液两相以及少量的气相组成,且固相包含粒径差异巨大的颗粒,因此泥石流内部作用力非常复杂(Bagnold, 1954; Johnson et al.,1970; Savage, 1979; Iverson, 1997; 费祥俊等, 2004; Pitman et al.,2005; 王沁等, 2005; Takahashi, 2007; Deng et al.,2011)。
在我国泥石流研究中,运动阻力计算方面取得了一系列研究成果(钱宁等, 1984)。费祥俊等(2004)根据泥石流中固体颗粒运动形式的不同,提出非均质两相流模型求解固液两相分界粒径。沈寿长(1998)对液相采用宾汉体模型,对固相采用膨胀体模型,在考虑两相之间的相互作用的基础上,提出两相流应力本构关系。王兆印等(2001)的研究表明泥石流的固液两相可具有相对运动; 铺床作用使黏性泥石流出现明显的减阻。祁龙(2000)认为黏性泥石流阻力的增加主要由推移质运动造成。樊赟赟等(2010)分析了固液两相的阻力。在计算中,固相阻力往往被简化成一个统一值(钱宁等, 1984; 祁龙等, 2000; 费祥俊等, 2004)。然而固相的组成复杂,不同泥石流固相的流动速度、体积比浓度、颗粒级配等差异巨大,导致运动阻力坡降大不相同,文献调查中尚未发现对这些影响因素的系统性的试验研究。由于阻力的理论计算困难,泥石流防治规划设计部门从工程实用角度提出泥石流阻力计算公式。我国泥石流灾害分布广泛,观测资料多,因此产生了很多地区性的经验公式。杜榕桓等(1987)根据泥石流泥深、流速等的观测资料,用综合糙率反映黏性泥石流内部及外部的综合阻力因子。
旋转水槽试验作为泥石流运动的物理模拟试验是最近才引起人们的注意。旋转水槽可以看作是底面微弯的传统水槽(王兆印等, 2001)绕固定点旋转的试验装置。旋转水槽试验由物理学研究中的旋转鼓试验(Chou et al., 2012)演变而来,早先被当作流变仪的替代设备用来测定泥石流的流变参数(Huizinga, 1996; Kaitna et al., 2007)。另一方面,Leonardi et al.(2015)在2015年发表的旋转水槽试验中观测到了固体颗粒不均匀分布现象和清晰的固液两相分离现象。考虑到这两个现象符合野外泥石流运动的特征(王兆印等, 2001; 费祥俊等, 2004),而且旋转水槽试验中固液两相形成稳定循环(stationary recirculating)流动,因此Leonardi et al.(2015)认为旋转水槽试验可作为泥石流的物理模拟手段。
本研究使用自主研发的旋转水槽,通过控制线速度制作稳定循环流动的泥石流。通过实测泥石流阻力坡降和流动速度,探索泥石流阻力坡降的速率效应。本项目的试验研究成果为泥石流制作和阻力坡降测量开辟新途径; 理论研究成果为进一步研究泥石流阻力坡降规律奠定基础。
1 试验方法
1.1 试验设备与土样
根据Leonardi et al.(2015)的试验原理,本项目研发的旋转水槽试验设备 (图1)由3部分组成:旋转水槽、动力控制与传动装置和摄影系统。其中旋转水槽的直径30cm,槽宽3cm,材质为有机玻璃。动力由电机提供,由计算机控制电机转动速度。摄影系统采用每秒25帧的摄像速度。
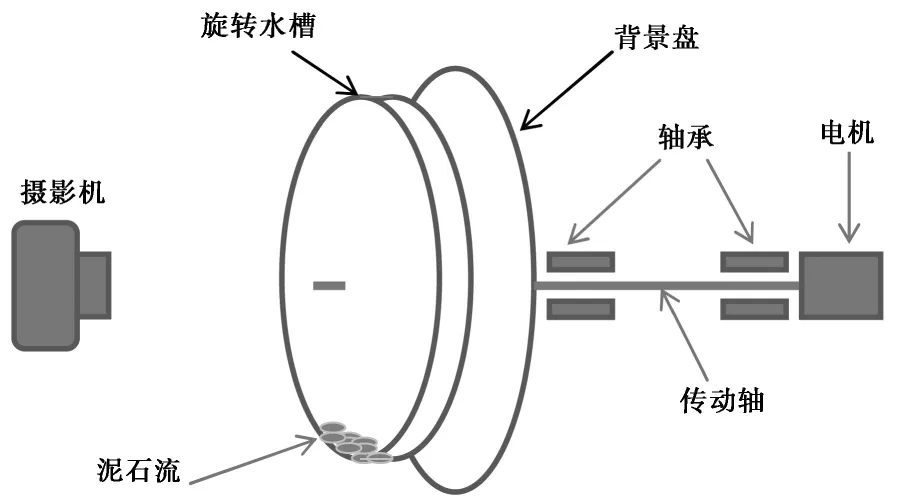
图1 旋转水槽试验设备组成简图
使用在野外泥石流沟(四川省汶川县七盘沟)沟口表层采集的土样,其中黏土5%、砂67%、砾石28%,不含粒径10mm以上的颗粒。泥石流容重γm=1.46t·m-3,根据费祥俊等(2004),这种泥石流介于稀性泥石流和黏性泥石流之间。泥石流平均速度v可由转速控制,依据试验中泥石流的运动状况,合理确定v的上下限。
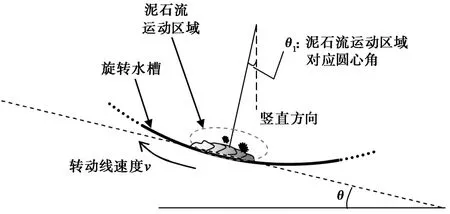
图2 旋转水槽试验实测阻力坡降示意图
1.2 阻力坡降测量方法
旋转水槽试验通过控制线速度v(依次为: 1.88、0.94、0.47、0.24和0.12m·s-1)制作泥石流,泥石流自动在一定区域内形成稳定循环运动 (图2); 此时的阻力坡降J等于槽底坡降tanθ,可以实测。例如在图2 中:θ=θ1,其中,θ1可根据摄影记录测定。在试验中,由于泥石流形状并不规则(例如有“龙头”、“龙尾”等),而粗颗粒(砾石)所在区域相对比较规则,因此测定粗颗粒所对应的圆心角θg,以近似替代θ1的值,即以粗颗粒对应的坡降Jg近似替代J。即:
(1)
2 试验结果与讨论
(1)制作了稳定循环的泥石流 (图3)。稳定循环流动现象与国外同行(Leonardi et al., 2015)观测到的现象一致,但本项目预研试验中使用的是宽粒径分布土样,且无固体颗粒黏接于槽底的现象。
(2)观测到泥石流形成的“龙头”和颗粒弹跳现象 (图3a)。与水槽试验观测结果一致(Savage, 1979)。此现象未见Leonardi et al.(2015)报道。
(3)观测到低阻力坡降现象。图3b观测到的阻力坡降为tan7°,这个阻力坡降属于比较低的坡降,处在野外泥石流沟常见的沟谷坡降范围内。图3c观测到的阻力坡降则低至tan1°(图3c)。考虑到图3c中的固液两相可能实际上已经分离,所以这种极低的阻力坡降在野外泥石流中可能只是暂时现象,难于观测。但图3c的试验也从一个侧面证实,泥石流可能出现非常低的阻力坡降。此现象未见Leonardi et al.(2015)报道。
(4)观测到固液相分离现象 (图3d)。此现象与野外观测结果一致(王兆印等, 2001); 与Leonardi et al.(2015)观测到的现象一致。
(5)观测到剪切速率效应。例如:v为0.94m·s-1的情况下,阻力坡降低J是tan7°(图3b);v为0.47m·s-1的情况下,J是tan1°(图3c)。此现象与Leonardi et al.(2015)观测到的现象一致。
图4为(v/v0)-Jg关系(其中,v0=0.47m·s-1,对应于固液相不分离的最小v值)。在4>v>1的情况下,砾石颗粒处于固液两相流的中部或前部,即砾石颗粒可随两相流一起运动 (图3a、图3b和图3c)。此时Jg与J大致相等,且Jg随log(v/v0)的增加大致成线性上升,证明阻力坡降随泥石流速率的增加而增加,这种线性关系与曼宁公式描述的关系有一定差异,但同样证实了阻力坡降具有显著的速率效应。在v<0.47m·s-1的情况下,砾石颗粒处于固液两相流的后部或已经脱离固液两相流,此时的θg只能用来评价砾石本身与槽底的摩擦阻力,不能用来评价泥石流的阻力坡降J。事实上,此情况下的tanθg随log(v/v0)的增加大致成线性减小 (图4)。

图3 旋转水槽试验结果
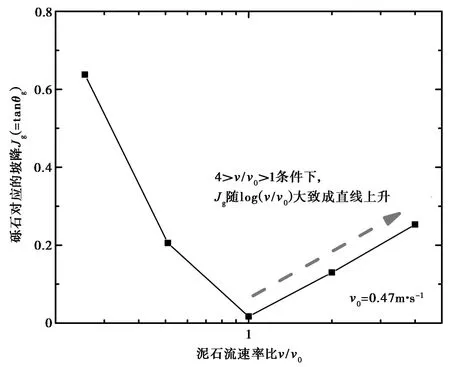
图4 logv-Jg关系
目前的旋转水槽试验的局限性在于: (1)试验中的固液两相流体缺乏通过“头冲尾淤”与沟床残留层进行物质交换。(2)宽粒径分布土样取自沟口表层,固体颗粒最大粒径不超过10mm,但实际野外泥石流沟底的固体颗粒粒径远远大于10mm,尺寸效应可能非常大,在今后的研究中需要进一步研究这种尺寸效应。(3)本实验研究尚处于起步阶段,试验成果需要进一步与相应的传统水槽和大型沟道试验成果以及野外观测结果比较。
3 结 论
本研究使用自主研发的旋转水槽制作稳定循环流动的泥石流,通过实测泥石流阻力坡降和流动速度,探索泥石流阻力坡降的速率效应。本项目的试验研究成果为泥石流制作和阻力坡降测量提供新途径。通过本课题的试验研究,可得到如下结论:
(1)在旋转水槽试验中,可以通过控制线速度v制作在一定区域内稳定循环运动的泥石流。此时的阻力坡降J等于槽底坡降tanθ,可以实测。
(2)在旋转水槽试验中,可以观察到“龙头”、颗粒弹跳、低阻力坡降、固液相分离、剪切速率效应等现象。这些室内观测结果印证了野外观测结果。
(3)在一定的流动速度范围内(本研究中1.88m·s-1>v>0.47m·s-1),且J随log(v/v0)的增加大致成线性上升(其中,v0=0.47m·s-1)。这种线性关系与曼宁公式描述的关系有一定差异,但同样证实了阻力坡降具有显著的速率效应。如果泥石流运动速率过低(本研究中v<0.47m·s-1),泥石流会出现固液两相分离现象,砾石(粒径>2mm)运动明显落后于液相运动。
Bagnold R.A. 1954. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear[C]∥Proceedings of the Royal Society of London. London, England:[s.n.], 225(1160): 49~63.
Chou S H,Hsiau S S. 2012. Dynamic properties of immersed granular matter in different flow regimes in a rotating drum[J]. Powder Technology,226: 99~106.
Deng J L,Nawir H,Tatsuoka F. 2011. Effects of viscous property and wetting on 1-D compression of clay and model simulation[J]. Soils and Foundations,51(5): 897~913.
Huizinga R J. 1996. Verification of vertically rotating flume using non-Newtonian fluids[J]. Journal of Hydraulic Engineering,122(8): 456~459.
Iverson R. 1997. The physics of debris flows[J]. Reviews of Geophysics,35(3): 245~296.
Johnson A M,Rahn P H. 1970. Mobilization of debris flows[J]. Zeitschrift fur Geomorphologie,9(S): 168~186.
Kaitna R,Rickenmann D,Schatzmann M. 2007. Experimental study on rheologic behaviour of debris flow material[J]. Acta Geotechnica,2(2): 71~85.
Leonardi A,Cabrera M,Wittel K F,et al. 2015. Granular-front formation in free-surface flow of concentrated suspensions[J]. Physical Review E, 92(5):(052204)1~13.
Pitman E.B,Le L. 2005. A two-fluid model for avalanche and debris flows[J]. Philosophical Transactions of the Royal Society(Series A),363: 1573~1601.
Savage S B. 1979. Gravity flow of cohesionless granular materials in chutes and channels[J]. Journal of Fluid Mechanics,92(1): 53~96.
Takahashi T. 2007. Debris flow: mechanics, prediction and countermeasures[M]. Leiden: Taylor & Francis.
崔鹏,唐邦兴. 1993. 泥石流学科的发展和对策[J]. 地球科学进展,8(2): 14~18.
杜榕桓,康志成,陈循谦,等. 1987. 云南小江流域泥石流综合考察与防治规划研究[M]. 重庆:科学技术文献出版社重庆分社, 1987.
樊赟赟,王思敬,王恩志. 2010. 基于结构两相阻力分析的泥石流堆积形态研究[J]. 工程地质学报,18(1): 100~104.
费祥俊,舒安平. 2004. 泥石流运动机理与灾害防治[M]. 北京:清华大学出版社.
祁龙. 2000. 黏性泥石流阻力规律初探[J]. 山地学报,18(6): 508~513.
钱宁,王兆印. 1984. 泥石流运动机理的初步探讨[J]. 地理学报,39(1): 33~43.
沈寿长. 1998. 泥石流应力本构关系[J]. 水利学报,(12): 16~22.
王沁,姚令侃,何平,等. 2005. 泥石流入汇主河的格子Bohzmann 模拟[J]. 自然灾害学报,4(3): 29~33.
王兆印,崔鹏,余斌. 2001. 泥石流的运动机理和减阻[J]. 自然灾害学报,10(3): 37~43.
JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0981- 11
EFFECTS OF FLOW RATE ON FRICTION SLOPE OF DEBRIS FLOW WITH ROTATING FLUME TESTS
This paper uses a newly developed rotating flume experiment apparatus. The friction slope and flowing rate of the debris flow are measured to evaluate the effect of flow rate on the friction slope. In the rotating flume experiment, a stationary recirculating debris flow is produced by controlling the rotating ratev.The friction slopeJof the debris flow is experimentally evaluated by measuring the tangential slope of the flume. In the experiments, the properties of debris flow are observed, including the shape of the head, the jump of large particles, the low friction slope, the segregation of solid phase from liquid phase and the flow rate effect. The experimental results show that the magnitude ofJincreases with the increasing flow ratevunder a certain conditions onv(e.g.1.88m·s-1≥v>0.47m·s-1in this research).The segregation of solid phase from liquid phase occurs whenvis too small(e.g.v<0.47m·s-1in this research).The displacement rate of gravels is much lower than the flow rate of the liquid phase. The experimental results provide an alternative method of producing debris flow and an alternative measurement method of friction slope. They also provide an experimental support for the further researches on the flow rate effect of debris flow.
Debris flow, Friction slope, Flow rate, Rotating flume test
10.13544/j.cnki.jeg.2016.05.029
2016-06-17;
2016-07-26.
高等学校博士学科点专项科研基金新教师类(20120073120020), 地质灾害防治与地质环境保护国家重点实验室开放基金(SKLGP2013K022)资助.
邓检良(1976-),男,博士,讲师,主要从事土构造物长期性能和工程地质防灾减灾方面的教学和科研. Email: dengjianliang@sjtu.edu.cn
P642.3
A
