WA联合ELM与OS-ELM的滑坡位移预测模型*

李骅锦 许 强 何雨森 魏 勇



WA联合ELM与OS-ELM的滑坡位移预测模型*

李骅锦①许 强①何雨森②魏 勇①

滑坡累积位移监测曲线往往呈现出复杂的非线性增长特性，对此建立了不少相关的预测模型，而以往的预测模型存在着许多不足。本文基于小波函数(Wavelet Analysis， WA)，ELM与OS-ELM，提出一种名为WA联合ELM、OS-ELM的预测方法。首先，该方法基于小波函数，将滑坡累积位移分解成受内部地质条件影响的趋势项和受外部影响因子影响的周期项； 然后，基于ELM与OS-ELM分别对趋势项和周期项进行预测； 最后将趋势项和周期项的预测值叠加得到累积位移的预测值。结果表明，小波函数得到的趋势项展现出良好的趋势性，而周期项也展现出良好的周期性； 以Sigmoid方程为核函数，隐含层神经元个数为33的ELM模型能准确高效对趋势项进行预测，而以RBF方程为核函数，隐含层神经元个数为100的OS-ELM模型能准确高效对周期项进行预测； 累积位移预测数据的RMSE分别为0.1423和0.1315，预测结果相对较好，能够在滑坡位移预测领域发挥一定的作用。

滑坡累积位移 非线性特性 位移预测 小波函数 ELM OS-ELM

0 引 言

滑坡是一种常见且危害较大的地质灾害，现在已经成为一类关注度极高的环境地质问题。滑坡的发生往往造成公路、供水供电设施、民居、农渠农田与经济林被毁，招致大面积交通堵塞、停水停电，居民家园被毁，甚至多人伤亡，给当地居民带来重大的人员伤亡和财产损失，引起不良的社会影响(许强等， 2016)。由于滑坡体受内部地质条件与外部环境影响因子的影响，累积位移监测曲线往往表现出复杂的非线性增长变化特性(许强等， 2008， 2009)。因此，研究如何利用位移监测曲线对滑坡进行准确预测预报对减少滑坡带来的危害将显得十分重要。开展滑坡位移预测预报的研究是当今国内外地质灾害研究领域之前沿热点课题，大量数据挖掘方法如神经网络模型(刘晓等， 2005; Pradhan et al.， 2010b; Chen et al.， 2013; Lian et al.， 2015; Mohamad et al.， 2015)、小波变换模型(Andrea et al.， 2002； Li et al.， 2009; Ebadi et al.， 2013; Doglioni et al.， 2014; 黄发明等， 2015)、时间序列模型(Robert et al.， 2006; Nicola et al.， 2010; Xu et al.， 2011; Du et al.， 2013; 彭令等， 2013)、灰色系统模型(Liu et al.， 2004; 吴益平等， 2007; Li et al.， 2012; Ren et al.， 2015)和学习训练机模型(姜谙男等， 2006; 杜娟等， 2009; Lins et al.， 2012; Bui et al.， 2012; Lian et al.， 2013; Abdi et al.， 2013; Liu et al.， 2014)被运用到了滑坡位移预测的研究中。部分研究成果虽取得了较好的预测结果，但在模型参数的选择、模型核函数的确定等方面仍有改进的空间。例如，Lian et al.(2015)运用神经网络算法，建立了不同环境因子与不同训练函数的神经网络模型，然后耦合多种模型结果对滑坡位移进行预测，由于建立神经网络的参数的选择(如隐层数目)对经验要求很高，合理选择神经网络的参数也缺乏理论指导依据，也限制了它的推广； Li(2012)基于灰色系统GM(1， 1)与Verhulst模型，耦合两种模型对滑坡位移进行预测，但是模型没有剔除冗杂信息，有损预测精度； 彭令等(2013)基于时间序列分析理论与支持向量机，将滑坡位移数据分解为周期性位移项、季节性位移项与趋势性位移项，然后进行了滑坡位移的预测，模型很好地解决了复杂的非线性回归问题，但是没有对算法核函数的选取进行论证分析。

近年，一种名为极限训练机(Extreme learning machine， ELM)的单隐层前馈神经网络(single-hidden layer feedforward neural networks， SLFns)学习算法被提出(Zhu et al.， 2005; Huang et al.， 2006b)。该算法具有数学模型简单、训练学习速度快，能获得全局最优解以及对新样本的适应性强的优势(Huang et al.， 1998; Huang， 2003)，已经广泛运用到工程问题甚至滑坡位移预测问题的求解中，并且取得了不错的效果(Ouammi et al.， 2010; Zong et al.， 2011; Lian et al.， 2013; Yu et al.， 2014; Yoan et al.， 2015; 周超等， 2015)。该算法解决了神经网络隐含层数目难于确定的问题。

滑坡位移预测研究的核心是提高预测数据的精度，增量式学习框架方法为解决该问题提供了一种较为可行的途径。增量式学习框架方法的原理是将最新的训练样本实时嵌入原始训练模型中进行增强训练以最大程度发挥模型泛化能力强的特点(Li et al., 2013)，能有效提高训练和预测的精度。Liang et al.(2006)提出了一种在线序列极限训练机(online sequential-extreme learning machine， OS-ELM)，是一种增量式的SLFns算法。该模型的特点为训练数据分批代入，单轮封闭训练且单次及时更新网络权值，使模型泛化能力更强(Liang et al.， 2006)。但是OS-ELM算法中参数的选择在简化模型求解过程时也会引起网络输出层的波动，降低训练网络的稳定性； 而且当隐层节点数目较大时，过量训练也会降低模型的泛化能力(李扬等， 2015)。

研究滑坡位移数据，则需要从滑坡本身的变形机制入手，依据监测数据进而深入分析其位移变化规律与内部地质条件和外部环境影响因子间的内在联系。一般处理方法则是将监测数据分解为受内部地质条件影响的趋势项和受外部影响因子影响的周期项(张俊等， 2015)。趋势项与周期项则是滑坡位移信号在不同频率的展现(周超等， 2015)，而小波分析函数(Wavelet Analysis， WA)是一种免先验知识即可处理变化趋势复杂数据问题的方法，且已有研究证明小波函数具有处理滑坡位移数据的能力(Kuanda， 2010; Ren et al.， 2015; 周超等， 2015)。

基于上述问题与前人研究结果，本文综合考虑滑坡位移的影响因素，以长江三峡库区白水河滑坡这一位移监测数据跳跃性较为典型的滑坡为例。首先，基于小波函数将滑坡累积位移分解成趋势项和周期项； 然后，分别对趋势项和周期项进行预测，由于趋势项位移变形较为简单，本文基于ELM模型对其进行预测，对变形过程相对复杂的周期项，运用OS-ELM进行预测(预测前，为得到准确高效的预测结果，对ELM和OS-ELM的核函数与隐含层神经元数目进行了分析选择)； 最后，将预测得到的趋势项与周期项进行叠加得到累积滑坡位移的预测值，并分析预测精度。

1 位移响应分析及预测方法介绍

1.1 小波函数分解位移数据为趋势项和周期项

滑坡体受内部地质条件(地形地貌、岩性构造等)以及外部环境影响因子(库水位升降、降雨情况、人类工程活动等)影响，其累积位移监测曲线往往表现出复杂的非线性增长变化特性。相关研究表明，滑坡累积位移信号可以分解为趋势项、周期项与突变项(Du et al.， 2013; 许强等， 2004， 2008)。趋势项为滑坡形变主体变化趋势，主要由滑坡体内部地质条件决定； 周期项反映滑坡体受到场地环境因素的影响产生的位移波动，比如库水位升降、降雨情况等的周期性波动； 突变项为滑坡体受到地震、突然外部加载或人类工程活动等突发性事件作用所产生的响应位移，一般也具有较好的周期性(Du et al.， 2013)，可以将其归入周期项进行预测预报。

本文运用小波函数对滑坡累积位移监测数据进行分解。小波函数是一种窗口大小恒定且具有可变形态的频局部信号分析方法(Vincent et al.， 1999)，具有良好的时频识别特性与多分辨率特性，能全方位获得滑坡累积位移监测数据的信号细节(Ren et al.， 2015)。将滑坡累积位移监测数据作为一时间序列，运用基函数的平移与伸缩(Chellali et al.， 2010)对其进行分解。其中基函数的满足的容许条件为：

(1)

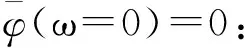
(2)

式中，a，b∈R; a≠0。a为伸缩因子，控制基本小波伸缩； b为平移因子，控制基本小波平移。

经过平移与伸缩后，得到子小波：

(3)

1.2 ELM预测趋势项

滑坡体在内部地质条件的影响下，主要体现在趋势项上。张俊等(2015)，Ren et al.(2015)和Du et al.(2013)等通过多项式拟合对趋势项进行预测。由于多项式函数对复杂非线性数据的处理有一定局限性，累积位移的突变部分被模糊处理(Du et al.， 2013; Ren et al.， 2015; 张俊等， 2015)，导致预测结果精度下降。

ELM是一种具有较强非线性识别能力(不如OS-ELM，但是为了简化模型计算，且趋势项较周期项具有简单的变化趋势，故本文运用ELM预测趋势项)的算法。其输出函数fL(x)的表达式(Huang et al.， 2006b)为：

(4)

其中，L为隐含层神经元数，ai和bi为隐层节点参数，βi表示连接第j个隐层和网络输出之间的外权，G(ai，bi，x)表示第j个隐层对应于趋势项归一化样本x的隐层节点输出，与核函数g(x)为的关系为：

(5)

其中，g： R→R为核函数，ai·x代表内权向量ai和样本x在Rn中的内积。

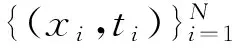
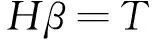
(6)

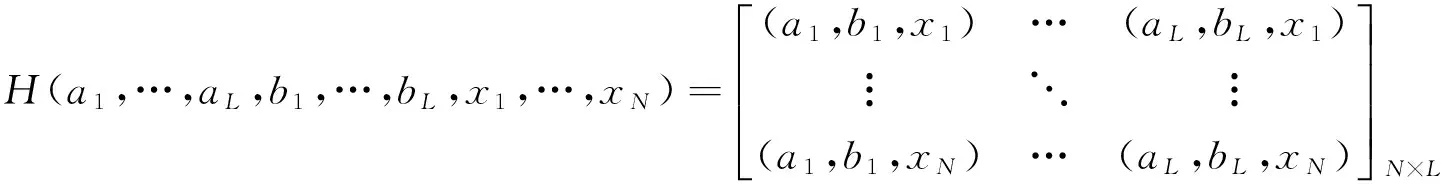
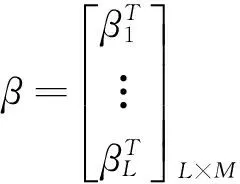
H为隐层输出矩阵，β通过最小二乘法进行求解：

(7)

在隐层输出为列满秩的条件下，利用Moore-Penrose广义逆(Ortega， 1987； Serre， 2002)可以得到下式：

(8)

一般而言，ELM算法常用的核函数(Kernel Function)有4种(Yoan et al.， 2010； Chorowski et al.， 2014)，形式如下：

(1)Sigmoid函数形式：

(9)

(2)Sine函数形式：

(10)

(3)hardlim函数形式：

R=2·hardlim(ai·x)

(11)

函数hardlim(x)定义核函数，当输入元素大于0时，函数返回1； 否则返回0。

(4)径向基函数(Radial basis function， RBF)形式：

(12)

式中，σ为实常参数，且σ=1-accu，accu为算法信度。

1.3 OS-ELM预测周期项

由于周期项主要受外部环境因子的影响，具有较趋势项更为复杂的变化趋势，传统分析方法难以解释其与外部环境因子的响应关系，使得周期项难以预测(Ren et al.， 2015)。非线性算法如神经网络(Neural networks)，支持向量机(Support Vector Machine， SVM)被运用到该类研究中(Mayoraz et al.， 2002; Biswajeet et al.， 2010; Ran et al.， 2010; Pradhan et al.， 2010a; Du et al.， 2013; Ren et al.， 2015; 张俊等， 2015)，取得了不错的结果。

为了提高滑坡累积位移趋势项的预测精度，本文引入具有增量式学习框架方法的OS-ELM算法。研究表明(Wang et al.， 2015; Nobrega et al.， 2015)，该算法通过SLFns的增量学习，能提高预测的精度。OE-ELM可分为如下两步(Liang et al.， 2006)：

第1步，初始化阶段

(2)计算初始化隐层输出矩阵H0，形式同式(5)；

(4)令k=0，为加入网络训练样本的批次，完成初始化。

第2步，序贯训练阶段

(2)计算其输出权重βk+1，更新βk+1与Pk+1；

(13)

(14)

上式中，Tk+1=[tNk，…，tNk+1]T。

(3)逐步开展训练以获得训练数据；

(4)当k= k+1，跳回第一步(3)，直到完成训练。

2 白水河滑坡概述

白水河滑坡位于长江主河道南岸(凸岸)，该处属三峡库区秭归县沙镇溪镇乐丰村(原白水河村)，距三峡大坝56km。滑坡为砂岩组成顺向岸坡，地势南高北低(北面为长江河谷)，南北高程相差约340m； 东西侧为近南北向山脊，并以基岩山脊为界； 总体地势上呈两脊相夹的不规则“圈椅”状。滑坡整体坡度约30°～35°，SN向长度约为600m， EW向宽度约为700m，滑体平均厚度约30m，体积约为1260×104m3。

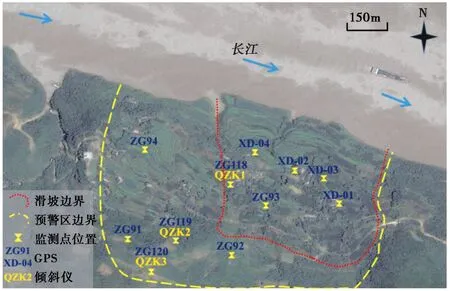
图1 白水河滑坡概况示意图(库水位125m)

白水河滑坡本是一处老滑坡，历史上发生过滑动。自2003年6月三峡水库135m蓄水后，在滑坡处开展了监测工作，由于滑坡前部长期位于长江水位之下，所以监测仪器从滑坡中部向后布置，监测仪器安放位置(图1)。由于三峡大坝建成后，库区蓄水使滑坡产生了明显的位移：在滑坡区中前部(即监测点XD-2处至前部)，该处滑坡位移增长明显，且与库水位响应关系显著； 在滑坡后部(即监测点XD-2处向后至滑坡边界处)，该处滑坡位移呈现“阶跃型”，但该处位移与库水位响应关系不强烈； 在滑坡边界与预警区边界之间的部位，滑坡累积位移小，变形速率仅为1.5～4.0mm·a-1(张俊等， 2015)。

由于白水河滑坡布置了多处监测点，且各处监测点的累积位移数据具有同步效应，而监测点ZG93与ZG118监测时间最长，且位于滑坡强变形区域，数据具有代表性，能最为完整反映滑坡位移的变化过程。因此，本文选取该两点监测数据(图2)，以验证本文建立预测模型的可靠性与准确性。

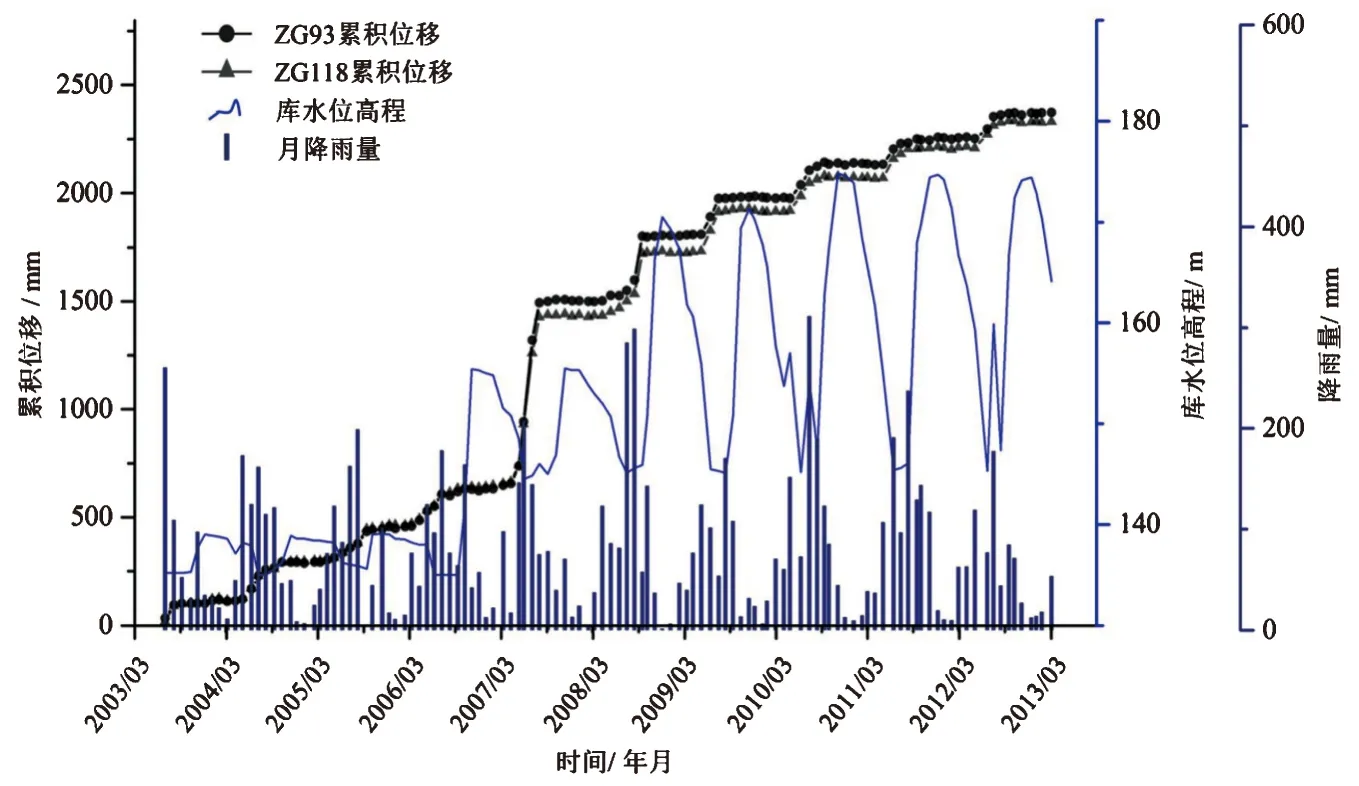
图2 2003～2013年滑坡累积位移与库水位高程、月降雨量数据

3 预测模型的应用与结果

由于滑坡累积位移受到内部地质条件与外部环境因子的影响，本文预测模型从趋势项和周期项进行预测分析。以ZG93和ZG118监测点为例，取2003年7月至2013年3月监测数据，对比分析。

3.1 小波函数结果

由于滑坡累积位移受到多种因素的影响，体现出混沌的非线性特性(周超等， 2015)，应用包伯成等(2009)为解决混沌与分岔，以提高小波精度而提出的DOG小波，将监测点ZG93与ZG118的累积位移分解为若干趋势项与周期项，计算结果(图3)。

分析图3 可知，该两处监测点位移趋势项数据完整且平滑，未出现数据尖点和拐点，较好地展示了位移数据变化的趋势； 两处监测点的周期项数据呈锯齿状，数据点局部极大极小值连续出现，表现出良好的周期性。

图3 小波函数计算结果

3.2 趋势项预测结果

根据小波函数得到的结果，运用ELM对其趋势项进行预测。由于常用ELM核函数有多种，故本文就所得趋势项数据，通过对比多种核函数情况下预测模型精度，以选择本模型的ELM核函数。

由于两处监测点趋势项数据具有相似的变化情况(图3)，故以ZG93趋势项数据为例，建立以式(9)、式(10)、式(11)和式(12)为核函数的ELM模型，为了控制对比模型为单变量，故其隐含层神经元个数均为5个。模型输入为时间，目标为趋势项位移； 取2003年7月至2010年3月数据为模型训练数据， 2010年4月至2013年3月数据为模型检验数据，通过均方根误差(Root Mean Square Error， RMSE)以评价预测模型精度，计算结果如下：

(15)

式中， ti为趋势项数据； yi为预测模型输出； N为样本数目。

分析表1数据可知，4种核函数预测模型均能完成趋势项数据的预测，输出完整的时间序列； 从预测模型表现而言，Sigmoid方程返回了最小的RMSE，Sine方程返回了最短的训练及检验时间，RBF方程返回了最优的最大误差，而hardlim方程得到了最差的预测效果，由此可见该核函数不适用于处理该类型数据； 就评价预测模型效果，在训练及检验时间与最大误差相差不大的情况下，一般取RMSE最小的作为评价标准(Wang et al.， 2014; Nobrega et al.， 2015)，所以本文趋势项ELM预测模型核函数采用Sigmoid方程。

表1 核函数预测模型对比

Table1 Comparison the results of four kernel function

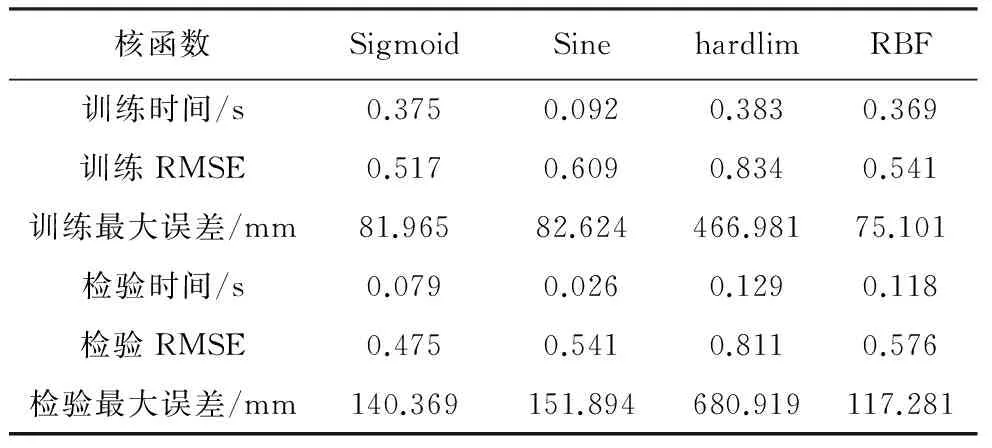
核函数SigmoidSinehardlimRBF训练时间/s0.3750.0920.3830.369训练RMSE0.5170.6090.8340.541训练最大误差/mm81.96582.624466.98175.101检验时间/s0.0790.0260.1290.118检验RMSE0.4750.5410.8110.576检验最大误差/mm140.369151.894680.919117.281

建立以Sigmoid方程为核函数的ELM预测模型时，需设置隐含层神经元个数为一循环数列，以找到最适宜的隐含层神经元个数。模型以时间作为输入，趋势项为目标； 取2003年7月至2010年3月数据为模型训练数据， 2010年4月至2013年3月数据为模型检验数据。模型计算得到不同隐含层神经元数目下的检验RMSE，根据计算可知，当隐含层数目为33时，趋势项检验数据的RMSE为0.01588，且随着神经元数目的增大，RMSE不再发生变化。计算结果(图4)。

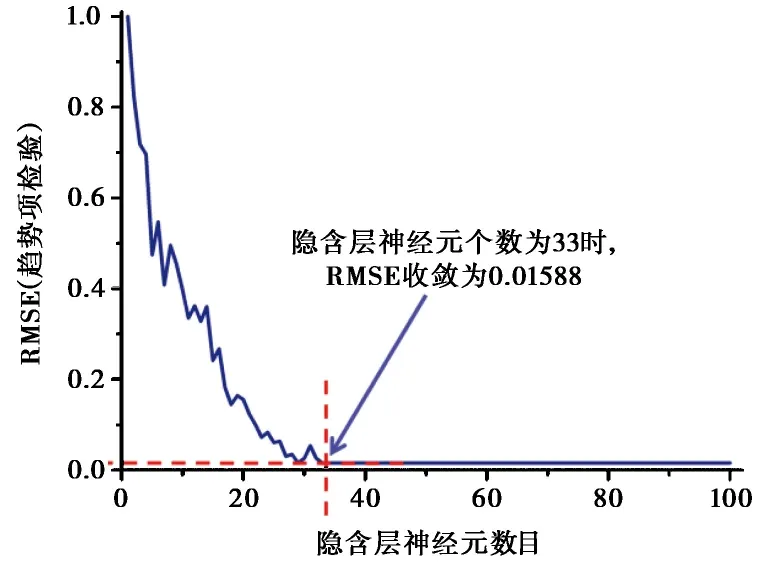
图4 趋势项RMSE与隐含层神经元数目关系图

取上述参数建立趋势项预测模型，以2003年7月至2009年3月数据为训练数据， 2009年4月至2010年3月为检验数据，预测2010年4月至2013年3月数据。预测结果(图5)。

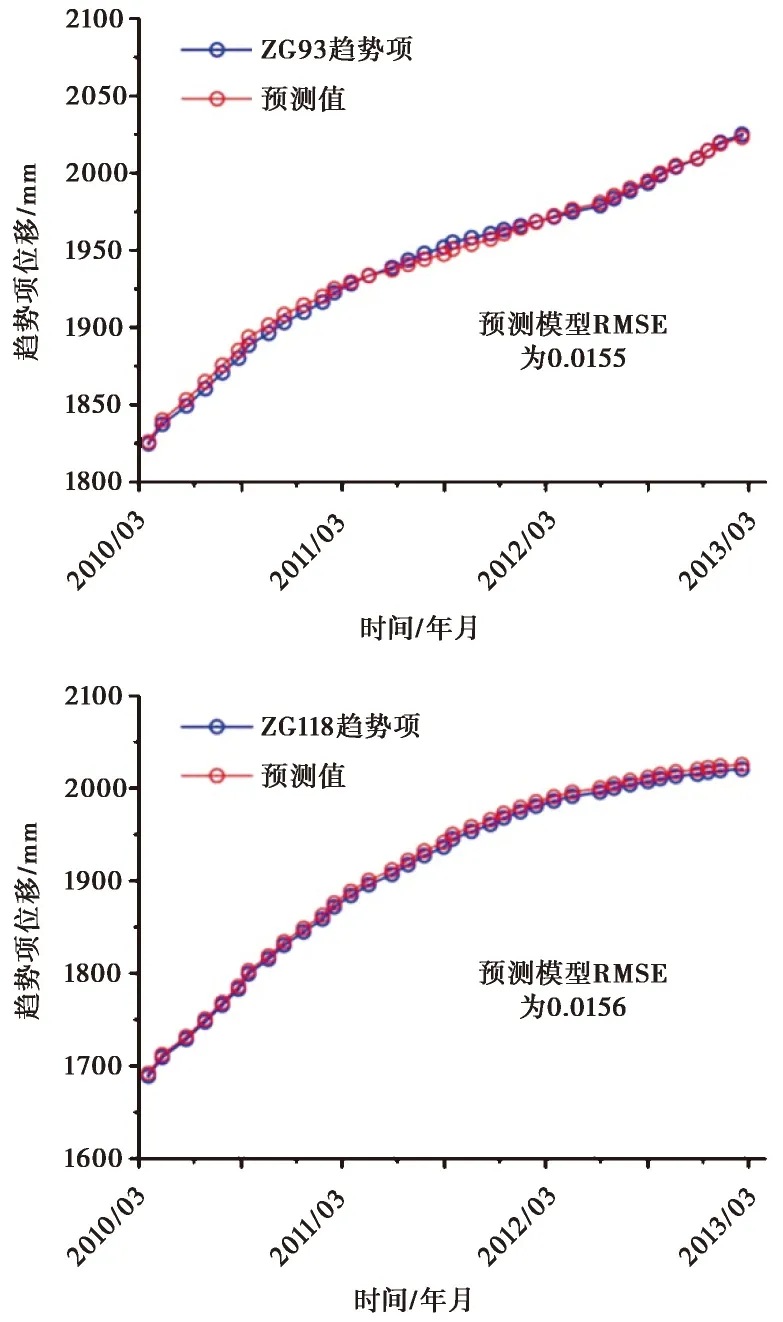
图5 趋势项预测效果

分析图5 可知，以Sigmoid为核函数的ELM能输出完整的预测时间序列，且预测数据返回RMSE值分别为0.0155和0.0156，预测结果良好(Wang et al.， 2014; Lian et al.， 2015; Nobrega et al.， 2015)。

3.3 周期项预测结果

滑坡周期项位移受多种外界因素影响，如何准确选取影响因子将直接影响预测模型的精度。根据张俊等(2015)和Du et al.(2013)研究白水河滑坡周期项影响因子的结果，本文选取当月降雨量、前1个月降雨量、前2个月降雨量、库水位高程、月间库水位变化量与累积位移年增量作为影响因子。以影响因子为输入，以周期项位移数据为目标建立OS-ELM模型。Wang et al.(2014)通过对OS-ELM的核函数进行对比分析，得出了RBF方程是最优核函数的结论，所以周期项预测模型核函数取RBF方程。

建立以RBF方程为核函数的OS-ELM预测模型，需设置隐含层神经元个数为一循环数列，以搜索模型最优的隐含层神经元个数。由于引入了累积位移年增量这一因子，而第一年的位移监测数据无法得到该值，故周期项预测模型取2004年6月至2010年3月数据为模型训练数据， 2010年4月至2013年3月数据为模型检验数据。两处监测点的预测结果(图6)。

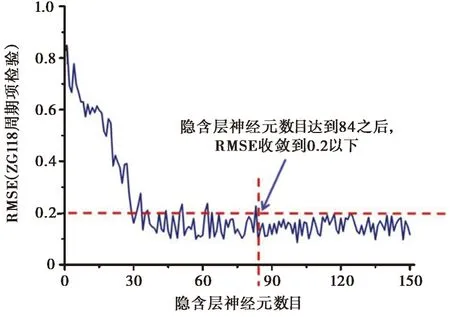
图6 周期项RMSE与隐含层神经元数目关系图

表2 周期项位移OS-ELM预测模型参数

Table2 Model parameters of periodic displacement prediction based on OS-ELM

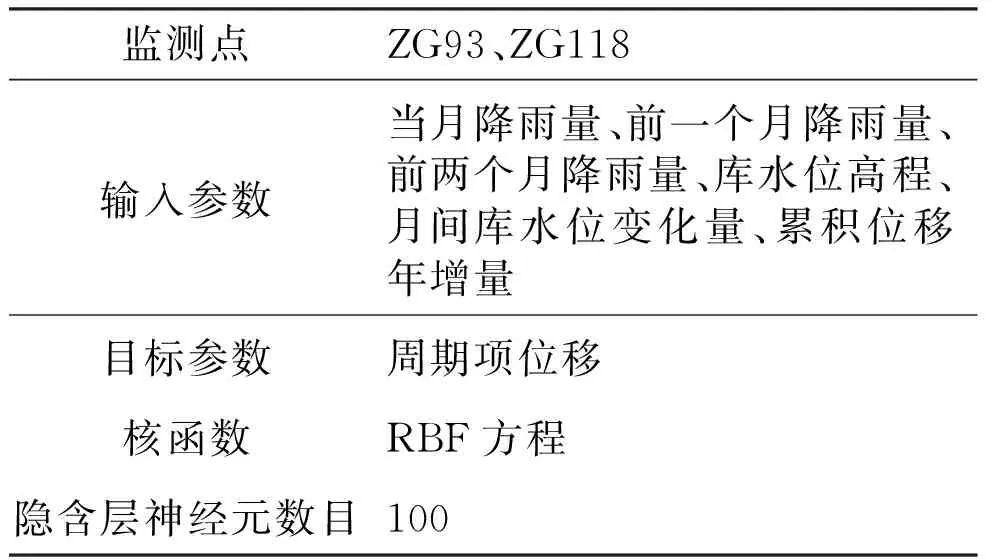
监测点ZG93、ZG118输入参数当月降雨量、前一个月降雨量、前两个月降雨量、库水位高程、月间库水位变化量、累积位移年增量目标参数周期项位移核函数RBF方程隐含层神经元数目100

分析图6 可知，周期项预测由于因子众多，且周期项变化较为复杂，所以预测精度不如变化规律较简单的趋势项 (图4 趋势项检验的RMSE收敛到一个具体数值，且结果较优； 图6 周期项检验的RMSE均没有收敛到一个具体数值，而是收敛到一个区间)。根据前人研究结果(Leuenberger et al.， 2015; Shang et al.， 2015; Shamshirband et al.， 2016)，RMSE值为0.2左右，预测模型得到良好的结果。当ZG93周期项检验的隐含层神经元数目到达73个，其RMSE收敛到0.2之下； 当ZG118周期项检验的隐含层神经元数目到达84个，RMSE也收敛到0.2之下，所以ZG93周期项预测模型隐含层神经元数目不应少于73个，ZG118周期项预测模型隐含层神经元数目不应少于84个。为了统一且尽量减少计算量，本文周期项预测模型隐含层神经元定为100个，随后取2004年6月至2009年3月数据为训练数据， 2009年4月至2010年3月为检验数据建立OS-ELM预测模型，预测2010年4月至2013年3月数据，模型核函数取RBF方程，计算结果(图7)。

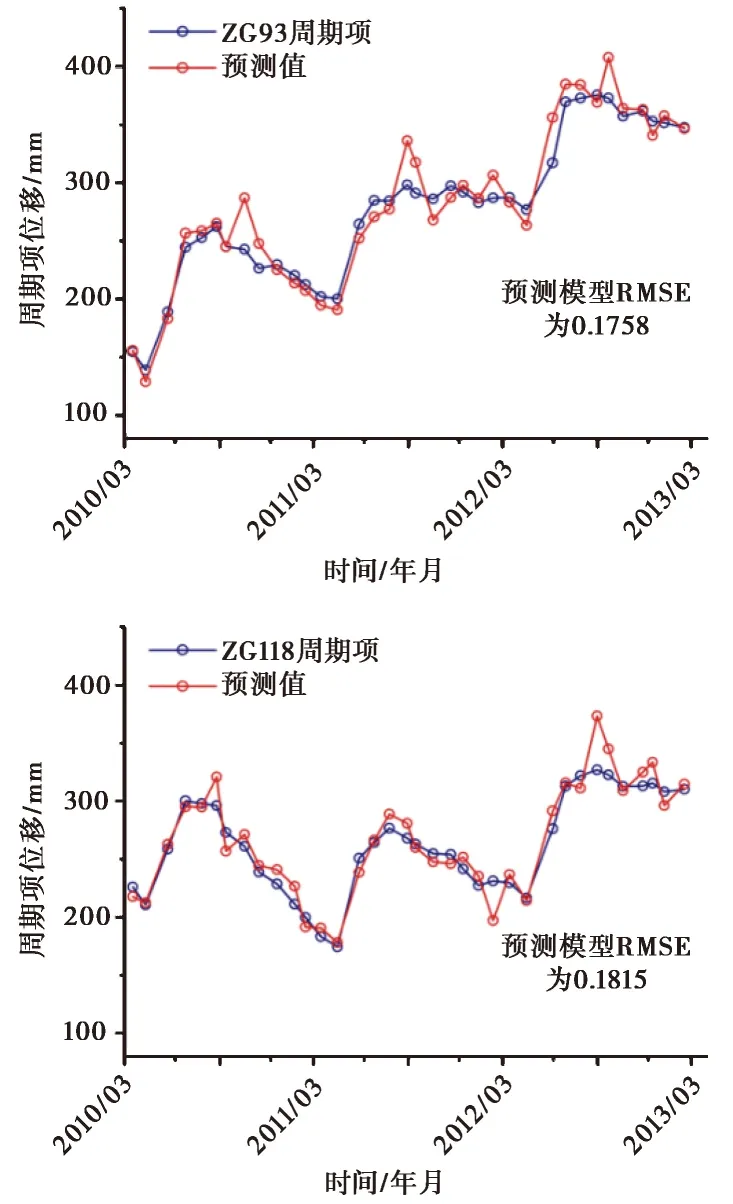
图7 周期项预测效果

图8 累计位移预测效果

分析图7 可知，OS-ELM预测滑坡位移周期项输出了完整的时间序列，预测值与周期项数据存在相似的变化规律； 由于周期项存在复杂的变化规律，其预测数据出现了多个跳点，一定程度上降低预测模型的精度。ZG93周期项预测返回RMSE为0.1785，ZG118返回RMSE为0.1815，虽然精度不如趋势项预测，但是也满足预测精度要求(Shamshirband et al.， 2016; Leuenberger et al.， 2015)。

3.4 累积位移预测结果

累积位移为趋势项位移与周期项位移的叠加，图8 所示，预测数据与累积位移数据存在相同的变化趋势，且模型的RMSE分别为0.1423与0.1315，对比前人预测结果良好。累积位移预测数据出现了几处跳点，且与周期项预测数据出现跳点的位置相同，而白水河滑坡周期项位移主要受库水位高程变化与降雨量的影响，其规律难寻，预测模型难免出现跳点。由趋势项位移预测结果 (图5)、周期项位移预测结果 (图7)和累积位移预测结果 (图8)可知滑坡位移预测的精度主要受周期项预测精度的影响。

4 结 论

本文通过WA联合ELM与OS-ELM模型，对三峡库区白水河滑坡的ZG93与ZG118监测点累积位移进行了预测。基于滑坡变形发展主要受内部地质条件和外部影响因子的思想，本文将累计位移分解成趋势项和周期项，趋势项数据完整且平滑，展现出良好的趋势性； 周期项数据局部极大极小值连续出现，也展现出良好的周期性； 然后通过研究发现，以Sigmoid方程为核函数，隐含层神经元个数为33的ELM模型能准确高效对趋势项进行预测，以RBF方程为核函数，隐含层神经元个数为100的OS-ELM模型能准确高效预测周期项； 最后将趋势项和周期项叠加得到累积位移的预测值，其RMSE分别为0.1423和0.1315，得到了相对较好的结果。综上分析可知，WA联合ELM与OS-ELM的滑坡位移预测模型能得到较为精确的预测结果，能够在滑坡位移预测领域发挥一定的作用。

Abdi M J，Giveki D. 2013. Automatic detection of erythemato-squamous diseases using PSO-SVM based on association rules[J].EngApplArtif Intel，26： 603～608.

AndreaPanizzoa， Giorgio Bellottib， Paolo De Girolamo. 2002. Application of wavelet transform analysis to landslide generated waves[J].Coastal Engineering，44(4)： 321～338.

Bao B C，Hu W，Liu Z，et al. 2009. Dynamical analysis of DOG wanelet mapping with dilation and translation[J]. Acta Physica Sinica，58(4)： 2240～2247.

Biswajeet P，Saro L. 2010. Delineation of landslide hazard areas on Penang Island， Malaysia， by using frequency ratio， logistic regression， and artificial neural network models[J].Environ Earth Sci，60： 1037～1054.

Bui DT，Pradhan B，Lofman O，et al. 2012. Landslide susceptibility assessment in Vietnam using support vector machines， decision tree and Nave Bayes models[J].Math Probl Eng., doi： 10.1155/2012/974638.

Chellali F，Khellaf A，Beelouchrani A. 2010. Wavelet spectral analysis of the temperature and wind speed data at Adrar， Algeria[J].Renewable Energy，35(6)： 1214～1219.

Chen HQ，Zeng ZG， 2013. Deformation prediction of landslide based on improved back propagation neural network[J].Cogn. Comput.，5(1)： 56～62.

Jan C， Wang J， Zurada J M. 2014. Review and performance comparison of SVM-and ELM-based classifiers[J].Neurocomputing，128(27)： 507～516.

Doglioni A，Simeone V. 2014. Geomorphometric analysis based on discrete wavelet transform[J].Environ Earth Sci，71(7)： 3095～3108.

Du J，Yin K，Lacasse S. 2013. Displacement prediction in colluvial landslides， Three Gorges Reservoir， China[J].Landslides，10： 203～218.

Du J，Yin KL，Cai B. 2009. Study of displacement prediction model of landslide based on response analysis of inducing factors[J].Chinese Journal of Rock Mechanics and Engineering， 28(9)： 1783～1789.

Ebadi L，Shafri H Z M，Mansor S B，et al. 2013. A review of applying second-generation wavelets for noise removal from remote sensing data[J].Environ Earth Sci，70(6)： 2679～2690.

Huang F M，Yin K L，Zhang G R，et al. 2015. Landslide groundwater level time series prediction based on phase space reconstruction and wavelet analysis-Support Vector Machine optimized by PSO algorithm[J].Earth science-Journal of China University of Geoscience，40(7)： 1254～1265.

Huang G B，Chen L，Siew C K.2006a. Universal approximation using incremental constructive feed forward networks with random hidden nodes[J].IEEE Trans Neural Netw，17(4)： 879～892.

Huang G B，Zhu Q Y，Siew C K.2006b. Extreme learning machine： theory and applications[J]. Neurocomputing，70(1-3)： 489～501.

Huang G B. 2003. Learning capability and storage capacity of two-hidden-layer feed forward networks[J].IEEE Trans Neural Netw，14(2)： 274～281.

Huang G B，Babri Ha. 1998. Upper bounds on the number of hidden neurons in feed forward networks with arbitrary bounded nonlinear activation functions[J].IEEE Trans Neural Netw，9(1)： 224～229.

Jiang A N，Liang B. 2006. Nonlinear time series prediction model for dam seepage flow based on PSO-SVM[J].Journal of Hydraulic Engineering，37(3)： 331～335.

Kuanda R B. 2010. A linear regression framework for predicting subsurface geometries and displacement rates in deep-seated， slow-moving landslides[J].EngGeol，114(1-2)： 1～9.

Leuenberger M and Mikhail K. 2015. Extreme Learning Machines for spatial environmental data[J].Computers & Geosciences，85： 64～73.

Li Y，Li G Q，Gu X P，et al. 2015. Transient stability assessment of power systems based on ensemble OS-ELM[J]. Transactions of China electro technical society，30(14)： 412～418.

Li Y, Gu X P. 2013. Application of online SVR in very short-term load forecasting[J].International Review of Electrical Engineering，8(1)： 277～282.

Li X Z，Kong J M，Wang Z Y. 2012. Landslide displacement prediction based on combining method with optimal weight[J].Natural Hazards，61(2)： 635～646.

Li C D，Tang H M，Hu X L，et al. 2009. Landslide Prediction Based on Wavelet Analysis and Cusp Catastrophe[J].Journal of Earth Science，20(6)： 971～977.

Lian C，Zeng Z G，Yao W，et al. 2015. Multiple neural networks switched prediction for landslide displacement[J].Engineering Geology，186： 91～99.

Lian C，Zeng Z G，Yao W，et al. 2013. Displacement prediction model of landslide based on a modified ensemble empirical mode decomposition and extreme learning machine[J]. Nat Hazards，66(2)： 759～771.

Liang N Y，Huang G B，Sarachandran P，et al. 2006. A fast and accurate online sequential learning algorithm for feedforward networks[J].IEEE Transactions on Neural Networks，17(6)： 1411～1423.

Lins I D，Moura M C，Zio E，et al. 2012. A particle swarmoptimized support vector machine for reliability prediction[J].QualReliabEngInt，28(2)： 141～158.

Liu Z B，Shao J F，Xu W Y，et al. 2014. Comparison on landslide nonlinear displacement analysis and prediction with computational intelligence approaches[J].Landslides，11(5)： 889～896.

Liu X，Zeng X H，Liu C Y. 2005. Research on artificial neural network-time series analysis of nonlinear displacement[J].Chinese Journal of Rock Mechanics and Engineering，24(19)： 3499-3,504.

Liu D A，Yang Z F，Tang C H，et al. 2004. An automatic monitoring system for theshiplock slope of Wuqiangxi Hydropower Station[J].Engineering Geology，76(1-2)： 79～91.

Mayoraz F，Vulliet L. 2002. Neural networks for slope movement prediction[J].Int J Geomech，2： 153～173.

Mohamad E T，Armaghani D J，Momeni E. 2015. Prediction of the unconfined compressive strength of soft rocks： a PSO-based ANN approach[J].Bull EngGeol Environ，74： 745～757.

NicolaCasagli， Filippo Catani， Chiara Del Ventisette. 2010. Monitoring， prediction， and early warning using ground-based radar interferometry[J].Landslides，7(3)： 291～301.

Nobrega J P，Oliveira A L I. 2015. Kalman filter-based method for Online Sequential Extreme Learning Machine for regression problems[J].Engineering Applications of Artificial Intelligence，44： 101～110.

Ortega J M. 1987. Matrix Theory[M].New York and London： Plenum Press.

Ouammi A，Dagdougui H，Sacile R，et al. 2010. Monthly and seasonal assessment of wind energy characteristics at four monitored locations in Liguria region(Italy)[J].Renew Sustain Energy Rev，14(7)： 1959～1968.

Peng L，Niu R Q，Wu T， 2013. Time series analysis and support vector machine for landslide displacement prediction[J].Journal of Zhejiang University(Engineering Science)，47(9)： 1672～1679.

Pradhan B，Buchroithner M F.2010a. Comparison and validation of landslide susceptibility maps using an artificial neural network model for three test areas in Malaysia[J]. Environ EngGeosci，16： 107～126.

Pradhan B，Youssef A M，Varathrajoo R. 2010b. Approaches for delineating landslide hazard areas using different training sites in an advanced artificial neural network model[J]. Geo-Spatial InfSci，13(2)： 93～102.

Ran Y F，Xiong G C，Li S S，et al. 2010. Study on deformation prediction of landslide based on genetic algorithm and improved BP neural network[J].Kybrtn，39： 1245～1254.

Ren F，Wu X L，Zhang K X. 2015. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of theShuping landslide in the Three Gorges， China[J].Environ Earth Sci，73(3)： 4791～4804.

Robert C J，Martin K，Roman L. 2006. Time series of count data： Modeling， estimation and diagnostics[J].Computational Statistics & Data Analysis，51(4)： 2350～2364.

Serre D. 2002. Theory and applications[M].New York： Springer.

Shamshirband S，Mohammadi K，Tong C W，et al. 2016. Application of extreme learning machine for estimation of wind speed distribution[J].ClimDyn，46： 893～1907.

Shang Z H G, He J Q. 2015. Confidence-weighted extreme learning machine for regression problems[J].Neurocomputing，148： 544～550.

Vincent J S，Ajit B，Raghuweer R，et al. 1999. Wavelet analysis of neuroelectric waveforms： A conceptual tutorial[J].Brain and Language，37(1)： 241～249.

Wang X Y，Han M. 2015. Improved extreme learning machine for multivariate time series online sequential prediction[J].Engineering Applications of Artificial Intelligence，40： 28～36.

Wang X Y，Han M. 2014. Online sequential extreme learning machine with kernels for nonstationary time series prediction[J].Neurocomputing，145： 90～97.

Wu Y P，Teng W F，Li Y W， 2007. Application of grey-neural network model to landslide deformation prediction[J].Chinese Journal of Rock Mechanics and Engineering，26(3)： 632～636.

Xu F，Wang Y，Du J，et al. 2011. Study of displacement prediction model of landslide based on time series analysis[J].Chinese Journal of Rock Mechanios and Engineering，30(4)： 746～751.

Xu Q，Peng D L，Qi X，et al. 2016. Dangchuan 2#landslide of april 29， 2015 in heifangtai area of gansu province： characteristics and failure mechanism[J].Journal of Engineering Geology，24(2)： 167～180.

Xu Q，Huang R Q，Yin Y P，et al. 2009. The Jiweishan landslide of June 5, 2009 in Wulong， Chonging： Characteristics and failure mechanism[J]. Journal of Engineering Geology，17(4)： 433～444.

Xu Q，Tang M G，Xu K X，et al. 2008. Research on space-time evolution laws and early warning-prediction oflandslides[J].Chinese Journal of Rock Mechanics and Engineering，27(6)： 1104～1112.

Xu Q，Huang R Q，Li X Z. 2004. Research progress in time forecast and prediction of landslides[J]. Advance in Earth Science，19(3)： 478～483.

YoanMiche， Anton Akusok， David Veganzones， et al. 2015. SOM-ELM-Self-Organized Clustering using ELM[J].Neurocomputing，165(1)： 238～254.

YoanMiche， Antti S，Patrick B，et al. 2010. OP-ELM：Optimally Pruned Extreme Learning Machine[J].IEEE Transactions on Neural N，21(1)： 158～162.

YU Q，Ymiche， Severin E，et al. 2014. Bankruptcy prediction using extreme learning machine and financial expertise[J].Neurocomputing，128(27)： 296～302.

Zhang J，Yin K L，Wang J J，et al. 2015. Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model[J].Chinese Journal of Rock Mechanics and Engineering，34(2)： 382～391.

Zhu Q Y，Qin N A K，Suganthan P N，et al. 2005. Evolutionary extreme learning machine[J].Pattern Recogn，38(10)： 1759～1763.

Zhou C，Yin K L，Huang F M. 2015. Application of the chaotic sequence WA-ELM coupling model in landslidedisplacement prediction[J].Rock and Soil Mechanics，36(9)： 2675～2680.

Zong W W，Huang G B. 2011. Face recognition based on extreme learning machin[J].Neurocomputing，74(16)： 2541～2551.

包伯成，胡文，刘中，等. 2009. DOG小波映射伸缩和平移的动力学分析[J].物理学报，58(4)： 2240～2247.

杜娟，殷坤龙，柴波. 2009. 基于诱发因素响应分析的滑坡位移预测模型研究[J].岩石力学与工程学报， 28(9)： 1783-I789.

黄发明，殷坤龙，张桂荣，等. 2015. 基于相空间重构和小波分析-粒子群向量机的滑坡地下水位预测[J].地球科学-中国地质大学学报，40(7)： 1254～1265.

姜谙男，梁冰. 2006. 基于PSO-SVM的大坝渗流监测时间序列非线性预报模型[J].水利学报，37(3)： 331～335.

李扬，李国庆，顾雪平，等. 2015. 基于集成OS-ELM 的暂态稳定评估方法[J].电工技术学报，30(14)： 412～418.

刘晓，曾样虎，刘春宇，等. 2005. 边坡非线性位移的神经网络-时间序列分析[J].岩石力学与工程学报，24(19)： 3499-3,504.

彭令，牛瑞卿，吴婷. 2013. 时间序列分析与支持向量机的滑坡位移预测[J].浙江大学学报(工学版)，47(9)： 1672～1679.

吴益平，滕伟福，李亚伟. 2007. 灰色神经网络模型在滑坡变形预测中的应用[J]. 岩石力学与工程学报，26(3)： 632～636.

许强，彭大雷，亓星，等. 2016. 2015年4.29甘肃黑方台党川2#滑坡基本特征与成因机理研究[J].工程地质学报，24(2)： 167～180.

许强，黄润秋，殷跃平，等． 2009. 2009年6.5重庆武隆鸡尾山崩滑灾害基本特征与成因机理初步研究[J]．工程地质学报，17(4)： 433～444.

许强，汤明高，徐开祥，等. 2008. 滑坡时空变化规律及预警预报研究[J].岩石力学与工程学报，27(6)： 1104～1112.

许强，黄润秋，李秀珍. 2004. 滑坡时间预测预报研究进展[J].地球科学进展，19(3)： 478～483.

张俊，殷坤龙，王佳佳，等. 2015. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J].岩石力学与工程学报，34(2)： 382～391.

周超，殷坤龙，黄发明. 2015. 混沌序列 WA-ELM 耦合模型在滑坡位移预测中的应用[J].岩土力学，36(9)： 2675～2680.

《崩滑地质灾害稳定性评价方法研究》

王根龙 叶万军 伍法权等著 上海交通大学出版社

内 容 简 介

本书是崩塌、滑坡地质灾害稳定性评价新方法研究，全书共分两篇十四章，系统阐述了边坡(滑坡)稳定性评价极限分析法和不稳定岩体(崩塌)稳定性评价计算方法。主要内容包括极限分析上限法原理、土质和岩质边坡稳定性评价极限分析上限解；崩塌地质力学分类、崩塌灾害机理及稳定性评价方法、崩塌灾害危险性分级与分区评价。

本书可供国土资源开发、地质灾害防治、水利水电、交通土建、矿山开采等领域以及高等院校、科研院所从事地质工程、岩土工程勘测设计的科研、教学人员参考使用，也可供减灾、防灾及相关业务人员使用。

有需要的读者可与王根龙博士取得联系。

联系电话：029-87821982 Email：wang2006@mail.iggcas.ac.cn

>PREDICTIVE MODELING OF LANDSLIDE DISPLACEMENT BY WAVELET ANALYSIS AND MULTIPLE EXTREME LEARNING MACHINES

LI Huajin①XU Qiang①HE Yusen②WEI Yong①

The curve landslide cumulative displacement is usually nonlinear. Hence， it is challenging to build predictive models with less error. In this paper， we propose a new methodology of embedding wavelet analysis with basic extreme learning machine(ELM) and online sequential extreme learning machine(OS-ELM)to predict the cumulative displacement. Firstly， by wavelet transformation， the cumulative function of displacement is discretized into periodic displacement and trend displacement. Secondly， basic ELM and OS-ELM are selected to predict the periodic displacement and trend displacement. Lastly， the cumulative displacement function is computed by ensembling the predicted periodic and trend displacement values. For basic ELM，a sigmoid function is selected as the kernel function and a single hidden layer with 33 nodes performs best. For OS-ELM，the prediction error reaches its minimum with 100 hidden nodes when the RBF function is selected as the kernel function. RMSE for ELM is 0.1423 and for OS-ELM is 0.1315. This methodology with high predictive accuracy performs better in comparison with other methods．

Landslide cumulative displacement， Nonlinear curve， Displacement prediction， Wavelet analysis， ELM， OS-ELM

10.13544/j.cnki.jeg.2016.05.001

2016-05-28;

2016-08-08.

国家重点基础研究发展计划(973)项目(2013CB733200)，国家创新研究群体科学基金(41521002)资助.

李骅锦(1991-)，男，硕士生，主要从事地质灾害预测评价与防治处理工作. Email：286069283@qq.com

P642.22

A