循环荷载作用下斜长花岗岩弹性模量演化规律*

胡 广 赵其华 何云松 韩 刚

HU Guang ZHAO Qihua HE Yunsong HAN Gang



循环荷载作用下斜长花岗岩弹性模量演化规律*

胡 广 赵其华 何云松 韩 刚

通过MTS815岩石力学试验机开展斜长花岗岩循环荷载试验，揭示循环次数、围压、含水率对斜长花岗岩弹性模量变化规律的影响，分析饱和与天然试样应力功、弹性应变能、耗散能随循环次数的演化规律。根据能量演化规律将岩石压缩变形破坏过程划分为4个阶段，研究各阶段切线模量与耗散能之间的关系。试验结果表明：(1)同一个应力水平切线模量随循环次数呈先增大后降低的趋势，其降低幅度随循环次数与应力水平增加而增大。(2)围压抑制了裂纹扩展，随围压增加切线模量弱化幅度减小。(3)饱和试样比天然试样切线模量弱化幅度大，说明水的存在加剧饱和试样内部结构损伤。(4)耗散能增加是引起切线模量弱化的内在因素，两者的变化规律呈现出很好的相关性。

循环荷载 斜长花岗岩 弹性模量 能量

HU Guang ZHAO Qihua HE Yunsong HAN Gang

0 引 言

在实际建设工程中，诸如边坡开挖、水位变动、道路交通、井下煤岩巷道等，岩土体经常会遇到循环荷载作用的情况。在循环荷载作用下，岩土体的力学特性与常规荷载作用有显著不同，因此有必要开展循环荷载条件下岩土体力学特性研究。

在过去的几十年里，岩石在循环荷载条件下的力学特性已被广泛研究。有学者认为循环荷载条件下岩石的膨胀包括岩石的蠕变与额外的损伤过程，提出引起膨胀的3种裂纹类型：应力驱使裂纹、应力衰减裂纹、疲劳裂纹(Scholz et al.，1979)。在岩石疲劳损伤方面，部分学者提出将岩石在循环荷载作用下的不可逆变形划分为3个阶段，即初始变形阶段、等速变形阶段和加速变形阶段。认为岩石疲劳寿命的主要影响因素是周期荷载的上限应力和幅值，并提出以变形来衡量岩石的破坏和强度(葛修润等， 1992， 2003)。在岩石变形破坏过程中，不可逆变形总是随着循环次数不断增加，但在不同的应力水平下，不可逆变形量的发展趋势有很大的差别。有学者认为其中存在一个“门槛”值(葛修润， 1987)，该值前后的不可逆变形量迥然不同，研究确定了疲劳门槛值为静态全过程体积变形的最小点，发现该点特征应力值略低于常规三轴试验中所谓的“屈服值”。部分学者从岩石宏观不可逆变形出发，提出将横向变形划分为两阶段(蒋宇等， 2004)。有学者通过研究了循环荷载作用下岩石疲劳力学性质，提出了基于内变量理论的岩石疲劳本构模型，较好地反映出岩石疲劳力学性质(王者超等， 2012)。

在循环荷载作用下岩石微观破坏方面也取得了很多重要的研究成果。部分学者利用扫描电镜(SEM)获取大量花岗岩细观微结构信息，从矿物晶体和微损伤形式两个角度定量分析了循环荷载作用过程中岩石的细观损伤特征(倪骁慧等， 2011a，2011b)。此外，研究了不同循环荷载频率作用下花岗岩细观疲劳损伤特征，以及不同循环荷载频率作用下细观尺度微裂纹扩展规律(倪骁慧等， 2011a，2011b， 2012)。

岩石变形破坏的根本原因是其内部结构的破坏，部分学者对循环荷载条件下岩石结构损伤和裂纹扩展规律进行了研究。有学者基于岩石CT细观试验，证实了岩石疲劳破坏存在门槛值，研究了循环荷载最大应力值的变化对岩石疲劳破坏的影响机理，得到了岩石细观疲劳损伤扩展的初步规律(葛修润等， 2001)。有学者开展了类玄武岩预制裂纹岩桥贯通模式研究(韩刚等， 2016)，将裂纹扩展-岩桥贯通过程划分为翼裂纹起裂、翼裂纹扩展和次生裂纹起裂及扩展、岩桥贯通3个阶段。

由于岩石材料不同，其力学特征也有显著的差别，部分学者开展了循环荷载条件下饱水砂岩排水变形试验研究，揭示应力幅度、平均应力、循环次数对累积不可逆变形的影响(Wichtmanni et al.，2007)。有的对煤岩在循环荷载作用下的强度、变形及疲劳损伤过程进行了研究，煤岩更容易发生疲劳破坏(杨永杰等， 2007)。部分学者开展了循环荷载条件下土石混合体力学特性研究，揭示了土石混合物的力学机理以及基本规律(徐文杰等， 2008)。在对岩盐的研究中，揭示了循环次数、循环频率对岩盐的抗压强度、弹性特征以及时效特征有重要的影响，认为基于循环荷载试验获取的特征参数相对传统试验更为合理(Fuenkajorn et al.，2010)。

弹性模量是岩石重要的力学性质之一，反应岩石抵抗变形的能力，也是岩土工程建设中重要的设计参数。众多学者对弹性模量进行了研究，有的研究了弹性模量对岩石抗压强度的影响(Palchik， 1999)，有的通过研究岩石的结构系数预测岩石的弹性模量(Alber et al.，2009)，有的基于遗传算法程序预测岩石的弹性模量(Beikin et al.，2013)。但目前尚未对循环荷载条件下的弹性模量演化规律与影响因素进行系统的研究。岩石经历多次循环荷载作用必然引起内部结构的损伤，通过研究弹性模量变化趋势揭示岩石变形破坏过程中内部结构损伤。本文针对循环荷载作用下斜长花岗岩弹性模量的演化规律与影响因素进行研究。

1 实验装置与方法

本次实验采用的是金沙江上游某水电站坝区边坡的斜长花岗岩，按照《水利水电工程岩体试验规程》(SL264—2001)的相关要求和试样精度制作了若干岩样，试件尺寸为直径50mm、高100mm标准圆柱体。本实验采用的试样主要矿物成分以斜长石和石英为主，占约90%。斜长石摩氏硬度为6～6.5，石英的摩氏硬度为7，都属于硬度较高的矿物。岩石实验借助于四川大学水利水电学院MTS815Teststar岩石试验机完成。

本次试验设置5MPa、10MPa、20MPa、30MPa 4种围压水平进行，并设置饱和试样(BX1、BX2、BX3、BX4，依次代表围压5MPa、10MPa、20MPa、30MPa)与天然试样(GX1、GX2、GX3、GX4，依次代表围压5MPa、10MPa、20MPa、30MPa)。试样采用循环等幅加、卸载模式，第1次循环峰值为20MPa，每次增幅20MPa。试验中静水压力段围压与轴压均采用应力控(FORCE控制)，加载速率0.05MPa·s-1。峰前轴压循环加、卸载阶段(80%峰值强度前，具体数值由常规三轴试验确定)，采用应力控制(FORCE控制)，轴压加载以及卸载速率为1.0MPa·s-1； 循环加、卸载结束后阶段(80%峰值强度后)，采用轴向位移(LDVT)控制，加载速率为0.02mm·min-1。循环加载示意(图1)。

图1 循环加载示意图

2 岩石变形能量演化规律

从能量角度分析，岩石在受力变形至破坏的整个过程中，始终与外界保持着物质和能量的交换，或将外部施加的机械能转变为岩石自身的内能，或将内部的应变能以一定的方式释放到外界(谢和平等， 2008)。根据热力学第一定律，考虑一个单位体积的岩体单元在外力作用下产生变形，假设该物理过程与外界没有热交换，即外力所做的功可认为全部被岩石吸收，外力做功所产生的能量U为(谢和平等， 2005； 李天斌等， 2015)：

U=Ud+Ue

2.1 饱和与天然状态下能量演化规律差异

图2为饱和与天然试样应力功随循环次数的变化曲线。可以看出：初始循环阶段应力功增长缓慢，之后应力功随循环次数迅速增加，近似指数增长。循环次数相同时，饱和试样吸收的应力功稍大于天然试样，两种状态下试样吸收应力功的能力差异不大。

图2 应力功随循环次数的演化关系

图3 弹性应变能随循环次数的演化关系

图3为试样可释放弹性能随循环次数的变化曲线。弹性应变能是岩石内部恢复变形释放的能量，表征岩石储存能量的能力。其增长趋势与循环次数的关系近似指数增长。围压与循环次数相同时，饱和与天然试样弹性应变能近似相等。

图4为耗散能随循环次数的变化曲线。耗散能用于岩石内部原始裂纹的压密与新裂纹的产生、扩展，以及已有裂纹面的摩擦与滑移，造成岩石内部结构损伤。从图中可以看出，初始循环耗散能增长缓慢，表明在低应力水平下裂纹的产生与扩展很少，仅存在原有裂纹的压缩与闭合； 循环中期耗散能近线性增长，岩样正处于裂纹稳定扩展阶段； 循环后期耗散能曲线突然变陡，耗散能急剧增加，裂纹迅速扩展与贯通，表明岩石内部损伤剧烈。相同应力水平下饱和试样耗散能大于天然岩样，表明在饱和状态下更多的能量用于裂纹的产生、扩展、贯通，其内部结构的损伤更强烈。

图4 耗散能随循环次数的演化关系

将试样在单次循环中的耗散能除以应力功得出耗散能比例，图5 为耗散能比例随循环次数的演化关系曲线。由图可以看出，耗散能比例曲线呈降低-水平-增加的趋势； 相同围压与循环条件下饱和与天然试样耗散能比例相差不大。

图5 耗散能比例随循环次数的演化关系

图6为能量极限值随围压的变化关系曲线。由图可知：天然试样极限应力功、极限弹性应变能、极限耗散能明显大于饱和岩样极限能量值，且两者的差值随围压增加而增大。表明天然岩样吸收应力功、储存弹性应变能的能力强于饱和试样，且随围压增加天然试样吸收、储存能量的能力增强。

图6 能量极限值随围压的变化关系

综上所述，两种状态下试样相同循环次数的应力功、可释放弹性应变能、耗散能相差很小，但天然试样能够经历更多的循环，承受更高的应力水平，其极限能量值远大于饱和试样。

2.2 岩石压缩阶段划分

一般而言，岩石三轴压缩过程可分为如下几个阶段：压密阶段、弹性阶段、裂纹稳定发展阶段、裂纹不稳定发展阶段、破坏后阶段(阳生权等， 2008)。基于应力功、弹性应变能、耗散能、耗散能比例对试样压缩变形阶段进行划分(以GX4为例，见图7)。

图7 GX4试样能量随循环次数演化规律

压密阶段(OA段)：应力功与弹性应变能增长缓慢，耗散能很小，耗散能比例较大，耗散能用于岩石原有裂纹的压密和颗粒之间的咬合，但岩石吸收的大部分能量仍以可释放弹性应变能储存起来。

弹性阶段(AB段)：经过压密，试样由非连续介质转变为似连续介质，应力功与弹性应变能近似指数迅速增加，耗散能近线性缓慢增加。这个阶段能量耗散较少，耗散能比例逐渐降低，岩石吸收的能量基本上转化为弹性能。

裂纹稳定发展阶段(BC段)：进入弹塑性变形阶段，试样内部出现微裂纹的萌生与扩展，岩石内部损伤逐渐加剧。应力功与弹性应变能呈指数增长，耗散能呈指数增长，耗散能比例近似水平直线。耗散能增长迅速，表明裂纹萌生、扩展加剧。

裂纹不稳定发展阶段(CD段)：裂纹的破裂机制发生了质的变化，应力集中效应显著。这个阶段应力功急剧增长，弹性应变能增长趋势减缓，耗散能显著增加，耗散能比例迅速变大。该阶段岩石储存弹性能的能力已接近极限。

3 弹性模量演化规律

3.1 弹性模量取值方法

常用的岩石弹性模量包括平均模量Eav、割线模量Es、切模量Et。平均模量(Eav)：应力-应变曲线弹性阶段的平均斜率。切线模量(Et)：应力-应变曲线任意应力处切线的斜率。割线模量(Es)：应力-应变曲线上某应力处与曲线原点之间直线的斜率，使用过程中一般取σc/2应力处与原点两点之间直线的斜率。国际岩石力学试验学会(ISRM)规定可采用割线模量E50作为非线性岩石的弹性模量。

由于本次试验采用的应力路径与加载方式，不容易求取每个循环的弹性变形阶段，平均模量与割线模量均不适用。根据Heap et al.(2008)提出的弹性模量计算方法，对循环曲线中每个回滞环进行3次多项式拟合的方法来确定任意应力下的切线模量。以围压10MPa(GX2)天然试样第10次循环加卸载曲线为例 (图8)，首先计算出应力差为20MPa时加载曲线和卸载曲线的切线弹性模量，如果两者的差值在10GPa之内，就认为应力-应变曲线处于弹性阶段，取加载曲线上的切线模量为这个回滞环的真实值，若两者差值大于10GPa，则不取 (图9)。此后应力每增加20MPa计算一次。

图8 GX2第10次循环加卸载曲线

图9 加卸载曲线斜率

3.2 循环次数与围压对弹性模量的影响

图10～图13 为不同围压的天然岩石切线模量随循环次数的变化关系。由图可知：同一个偏应力水平切线模量随循环次数增加有一个先增大的趋势，该过程仍然处于裂纹压密阶段，岩样内部原有裂隙随应力水平增加逐渐闭合，缺陷部位被压缩或压密，内部应力由软弱部分与坚硬部分共同承担转变为由坚硬部分承担或坚硬部分主要承担，岩石切线模量出现强化。

随循环次数增多，切线模量变化趋势由增大转变为不断减小，表征岩石内部裂纹萌生与扩展加剧。该过程中原有裂隙面之间出现摩擦与滑移，以及应力水平增加产生新的裂隙，塑性变形增加，切线模量随循环次数增加有不同程度的减小，相同应力水平的切线模量随循环次数呈现弱化的趋势。

图10 GX1试样切线模量随循环次数变化

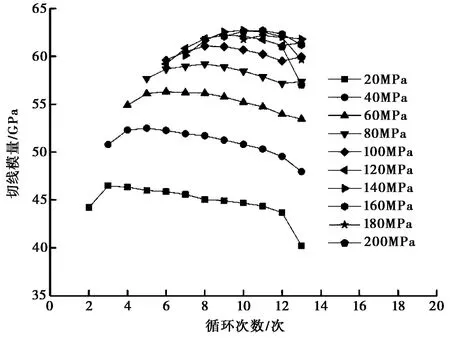
图11 GX2试样切线模量随循环次数变化

图12 GX3试样切线模量随循环次数变化

图13 GX4试样切线模量随循环次数变化

为了探究循环次数对切线模量的影响，取相同应力水平下切线模量的最大值作为该应力水平岩石裂纹的压密点(取为E0)。将相同应力水平压密点以后的切线模量除以E0定义为弱化系数，分析切线模量随循环次数的弱化程度(限于篇幅，仅以GX4为例，见图14)。

图14 GX4试样切线模量弱化系数演化规律

图14发现切线模量随循环次数的变化趋势有如下规律：(1)循环次数增加引起弱化系数不断降低，即循环增多切线模量降低幅度增大，加剧了裂纹萌生、扩展、贯通； (2)应力水平增加时，切线模量弱化幅度也会增大。图15 为天然试样应力差20MPa时不同围压的切线模量弱化系数，可以看出：除GX3外，试样随围压增加表现出良好的规律：随围压增加弱化系数降低幅度减小，即围压增大抑制试样内部结构损伤。

图15 天然试样弱化系数随循环次数变化关系(应力差20MPa)

图16 饱和试样弱化系数随循环次数变化关系(应力差20MPa)

大量的岩石力学试验已经揭示了岩石的损伤方式，微裂隙发展可以分为3种类型：应力诱导微裂隙，由应力增加而导致微裂隙的发展； 循环疲劳微裂隙，即由于循环荷载导致原生裂隙的张开与闭合时产生的新微裂隙； 时间引起微裂隙，即在一定的应力作用下随着时间的增加而产生的微裂隙。本次试验揭示了前两种微裂纹的产生，裂纹的产生是应力与循环次数共同作用的结果，而随时间产生的裂纹很少。

3.3 含水量对弹性模量的影响

由图17～图20 可知，总体上饱和试样与天然试样规律近似：随着裂纹与缺陷被压密或压缩切线模量逐渐增大，然后随着循环次数与应力增加切线模量呈现出弱化特性。相同围压条件下，图16 饱和试样与图15天然试样相比可知：(1)除BX4试样，饱和试样应力差为20MPa的弱化趋势与围压有明显的相关性； (2)相同循环次数饱和试样的弱化系数明显大于天然试样，即饱和试样切线模量弱化程度更大，说明水的存在加剧了饱和试样内部结构的损伤。

图17 BX1 试样切线模量随循环次数变化

图18 BX2试样切线模量随循环次数变化

图19 BX3试样切线模量随循环次数变化

图20 BX4试样切线模量随循环次数变化

4 讨 论

切线模量表征岩石应力-应变曲线的关系，反映内部微观结构损伤过程。岩石的能量是基于应力-应变曲线关系获取的岩石内部属性，表征岩石在循环加卸载过程中所处的状态，揭示岩石变形破坏规律。根据耗散能演化规律与切线模量的弱化规律，揭示岩石变形破坏过程。

图21 试样切线模量与耗散随循环次数变化关系

耗散能是岩样裂纹萌生、扩展、贯通的能量来源，反应岩石内部结构损伤程度，随循环次数增加，裂纹萌生与扩展加剧。由图21 可知，耗散能随循环次数增大是引起切线模量弱化的内在因素，两者的变化规律揭示了裂纹产生、扩展、贯通的整个过程，呈现出很好的相关性。压密阶段：耗散能很小，增长趋势缓慢，仅存在原有裂纹的压密，几乎不产生新的微裂纹，切线模量随循环次数增加。弹性变形阶段：高应力水平切线模量在增加，低应力水平切线模量已经出现弱化，耗散能近直线缓慢增长，仅有少量微裂纹产生。裂纹稳定发展阶段：所有应力水平下切线模量均出现弱化，耗散能呈指数快速增长，试样损伤加剧。裂纹不稳定发展阶段：耗散能急剧增长，主要用于裂纹萌生、扩展、贯通，加卸载曲线切线模量差值超过10GPa，已超出本文定义的弹性阶段，无法求得切线模量。

5 结 论

对循环加、卸载试验获取的数据进行处理分析，得出如下结论：

(1)根据能量演化规律将岩石压缩变形破坏过程划分为4个阶段，即压缩阶段、弹性阶段、裂纹稳定发展阶段、裂纹不稳定发展阶段。耗散能增大是引起切线模量弱化的内在因素，两者的变化规律呈现出很好的相关性，共同揭示裂纹产生、扩展、贯通的整个过程。

(2)相同围压与循环次数的饱和与天然状态试样应力功、可释放弹性应变能、耗散能相差很小； 但天然试样能够经历更多的循环，承受更高的应力水平，其极限能量值远大于饱和试样。

(3)同一个应力水平切线模量随循环次数增加呈先增大后降低的趋势。

(4)循环次数与应力水平增加造成切线模量降低幅度增大； 围压增加抑制裂纹扩展，切线模量弱化幅度减小； 饱和试样切线模量的弱化趋势更大，说明水的存在加剧了裂纹的扩展。

(5)本次试验揭示了裂纹的产生是应力与循环次数共同作用的结果。裂纹首先由应力增加引起，经由循环次数引起裂纹进一步扩展，造成试样内部结构的损伤。

Alber M，Kahraman S. 2009. Technical Note Predicting the uniaxial compressive strength and elastic modulus of a fault breccia from texture coefficient[J]. Rock Mechanics and Rock Engineering，42(1)： 117～127．

Beikin M，Majdi A，Givshad A D. 2013. Application of genetic programming to predict the uniaxial compressive strength and elastic modulus of carbonate rocks[J]. International Journal of Rock Mechanics & Mining Sciences，63(3)： 159～169．

Fuenkajorn K，Phueakphum D. 2010. Effects of cyclic loading on mechanical properties of Maha Sarakham salt[J]． Engineering Geology，112： 43～52．

Ge X R，Jiang Y，Lu Y D，et al. 2003. Testing study on fatigue deformation law of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering，22(10)： 1581～1585．

Ge X R，Lu Y F. 1992. Study on fatigue failure and irreversible deformation problem of rock under cyclic load[J]. Chinese Journal of Geotechnical Engineering，14(3)： 56～60．

Ge X R，Ren J Xi， Pu Y B，et al. 2001. Primary study of CT real-time testing of fatigue meso-damage propagation law of rock[J]. Chinese Journal of Geotechnical Engineering，23(2)： 191～195．

Ge X R. 1987. Study of deformation and strength behavior of the large-sized triaxial rock samples under cyclic loading[J]. Rock and Soil Mechanics，8(2)： 11～19．

Han G，Yang F，Liu Y，et al. 2016. Rock bridge coalescence mode of basalt-link materials with two pre-existing flaws under biaxial cyclic compression[J]. Journal of Engineering Geology，24(2)： 235～245．

Heap M J，Faulkner D R. 2008. Quantifying the evolutionofstatic elastic properties as crystalline rock approachesfailure[J]. International Journal of Rock Mechanicsand and Mining Sciences，45(4)： 564～573．

Jiang Y，Ge X R，Ren J X. 2004. Deformation rules and acoustic emission characteristics of rocks in process of fatigue failure[J]. Chinese Journal of Rock Mechanics and Engineering，23(11)： 1810～1814．

Li T B，Chen Z Q，Chen G Q，et al. 2015. An experimental study of energy mechanism of sandstone with different moisture contents[J]. Rock and Soil Mechanics， 36(S2)： 229～236．

Ni X H，LI X J，Zhu Z D, et al. 2012. Quantitative test study of meso-damage of granite under cyclic load with different Frequencies[J]. Rock and Soil Mechanics，33(2)： 422～427．

Ni X H，Li X J，Zhu Z D. 2011. Characteristics of meso-damage of granite samples subjected to dynamic uniaxial cyclic loading with different frequencies.[J]. Chinese Journal of Rock Mechanics and Engineering，30(1)： 164～169．

Ni X H，Zhu Z D，Li X J，et al. 2011. Quantitative test study of meso-damage of rock under cyclic load[J]. Rock and Soil Mechanics，32(7)： 1991～1995．

Palchik V. 1999. Influence of porosity and elastic modulus on uniaxial compressive strength in soft brittle porous sandstones[J]． Rock Mechanics and Rock Engineering，32(4)： 303～309．

Scholz C H，Koczynski T A. 1979. Dilatancy anisotropy and the response of rock to large cyclic loads[J]. Journal of Geophysical Research Atmospheres，84(10)： 5525～5534．

Wang Z C，Zhao J G，Li S C，et al. 2012. Fatigue mechanical behavior of granite subjected to cyclic load and its constitutive model[J]. Chinese Journal of Rock Mechanics and Engineering，31(9)： 1888～1900．

Wichtmanni T，Niemunis A，Triantafyllidis Th. 2007. Strain accumulation in sand due to cyclic loading： drained cyclic tests with triaxial extension[J]. Soil Dynamics & Earthquake Engineering，27(1)： 42～48.

Xie H P，Ju Y，Li L Y，et al. 2008. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering，27(9)： 1729～1740．

Xie H P，Ju Y，Li L Y. 2005. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles [J]. Chinese Journal of Rock Mechanics and Engineering，24(17)： 3003～3010．

Xu W J，Hu R L. 2008. Field horizontal push shear test for mechanical property of soil-rock mixtures under cyclic loading[J]. Journal of Engineering Geology，16(1)： 63～69．

Yang S Q，Yang J S. 2008， Rockmass mechanics[M]. Beijing： China Machine Press： 1～238．

Yang Y J，Song Y，Chu J. 2007. Experimental study on characteristics of strength and deformation of coal under cyclic loading[J]． Chinese Journal of Rock Mechanics and Engineering，26(1)： 201～205．

Zhu M L，Zhu Z D，Li G， et al. 2009. Experimental study of dynamic characteristics of granite under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering，28(12)： 2520～2526．

葛修润，蒋宇，卢允德，等. 2003. 周期荷载作用下岩石疲劳变形特性试验研究[J]. 岩石力学与工程学报，22(10)： 1581～1585．

葛修润，卢应发. 1992. 循环荷载作用下岩石疲劳破坏和不可逆变形问题的探讨[J]. 岩土工程学报，14(3)： 56～60．

葛修润，任建喜，蒲毅彬，等. 2001. 岩石疲劳损伤扩展规律CT细观分析初探[J]. 岩土工程学报，23(2)： 191～195．

葛修润. 1987. 周期荷载作用下岩石大型三轴试件的变形和强度特性研究[J]. 岩土力学，8(2)： 11～19．

韩刚，杨帆，刘宇，等. 2016. 双轴循环荷载条件下含预制裂纹类玄武岩岩桥贯通模式[J]. 工程地质学报，24(2)： 235～245．

蒋宇，葛修润，任建喜. 2004. 岩石疲劳破坏过程中的变形规律及声发射特性[J]. 岩石力学与工程学报，23(11)： 1810～1814.

李天斌，陈子全，陈国庆，等. 2015. 不同含水率作用下砂岩的能量机制研究[J]. 岩土力学，36(增2)： 229～236．

倪骁慧，李晓娟，朱珍德，等. 2012. 不同频率循环荷载作用下花岗岩细观疲劳损伤量化试验研究[J]. 岩土力学，33(2)： 422～427．

倪骁慧，李晓娟，朱珍德. 2011b. 不同频率循环荷载作用下花岗岩细观疲劳损伤特征研究[J]. 岩石力学与工程学报， 30(1)：164～169．

倪骁慧，朱珍德，李晓娟，等. 2011a. 循环荷载下花岗岩细观损伤量化试验研究[J]. 岩土力学，32(7)： 1991～1995．

王者超，赵建纲，李术才，等. 2012. 循环荷载作用下花岗岩疲劳力学性质及其本构模型[J]. 岩石力学与工程学报， 31(9)：1888～1900．

谢和平，鞠杨，黎立云，等. 2008. 岩体变形过程破坏过程的能量机制[J]. 岩石力学与工程学报，27(9)： 1729～1740．

谢和平，鞠杨，黎立云. 2005. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学， 24(17)： 3003～3010．

徐文杰，胡瑞林. 2008. 循环荷载下土石混合体力学特性野外试验研究[J]. 工程地质学报，16(1)： 63～69．

阳生权，阳君生. 2008. 岩体力学[M]. 北京：机械工业出版社： 1～238．

杨永杰，宋扬，楚俊. 2007. 循环荷载作用下煤岩强度及变形特征试验研究[J]. 岩石力学与工程学报，26(1)： 201～205．

朱明礼，朱珍德，李刚，等. 2009. 循环荷载作用下花岗岩动力特性试验研究[J]. 岩石力学与工程学报，28(12)： 2520～2526．

JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0891- 08

ELASTIC MODULUS’S EVOLUTION LAW OF PLAGIOGRANITE UNDER CYCLIC LOADING

This paper presents the increasing-amplitude cycle loading experiment of plagiogranite through the MTS815 rock mechanics testing machine. It examines the effects of number of cycle， confining pressure and moisture content on elastic modulus， and analyzes the variation of work stress，elastic strain energy and dissipated energy with increasing number of cycle. The process of rock compression deformation and failure is divided into four stages according to the energy change law. It researches the relationship between tangent modulus and dissipated energy. The experimental results show that：(1)The tangent modulus at the same stress level is increased and then decreased at the cycle times increases. Its decreasing amplitude increases as cycles and stress level increase. (2)The weakened amplitude of tangent modulus decreases with increase of confining pressure. (3)The weakened amplitude of tangent modulus of saturated samples is bigger than that of natural samples， which shows that water is aggravated damage on saturated samples. (4)The increase of dissipated energy is the cause of the tangent modulus weakening. The change rules of dissipated energy and tangent modulus are correlative．

Cyclic loading， Plagiogranite， Elastic modulus， Energy

10.13544/j.cnki.jeg.2016.05.018

2016-05-30;

2016-07-27.

国家重点基础研究发展计划(973)项目(2011CB013501)，国家自然科学基金项目(42272333)资助.

胡广(1991-)，男，硕士生，主要从事地质工程方面的研究工作. Email: 214764662@qq.com

简介： 赵其华(1965-)，男，博士，教授，博士生导师，主要从事岩石高边坡工程、地质灾害评价与治理设计等领域的科研与教学工作. Email: zhqh@163.com

P642.3

A