给定限界势结构生成算法的改进∗

李少芳，车 艳

(莆田学院信息工程学院，福建莆田 351100)

给定限界势结构生成算法的改进∗

李少芳∗，车 艳

(莆田学院信息工程学院，福建莆田 351100)

寻求最优联盟结构是NP-完全的，建立限界k＝n/2的最小搜索是搜索联盟结构图的最底二层及顶层，在最小搜索之后，不同算法采用不同的搜索单位和路径进行有选择地部分搜索，以尽快达到给定限界值。在实际应用中，充分利用同势的两个联盟同值或值相差不大的特征，研究最优势结构生改进算法效率。文中通过分析势结构间的关系，指出了给定限界的势结构生成算法中一些可以去除的冗余搜索集合，从两个方面改进了算法，并进行了相关结果的证明。

势结构(CCS);给定限界;多agent系统;算法改进

随着信息产业和经济全球化的加速发展，科技的进步与创新大大推动了企业之间的合作。企业合作创新不仅可以降低风险和减少成本，也能提高自身的创新能力，创造和开拓新市场，获取单个企业无法达到的协同效应。不同联盟结构下企业合作创新的利益分配问题是不同的。单个agent参加一个联盟的动机是为了更有效地完成任务，增加收益。投标者往往将多个拍卖品进行组合竞拍，既可以降低竞拍成本，又可以通过不同的商品组合来产生更好的价值。组合拍卖是银行不良资产的处置最有效率的方法[1]。在实际应用中，同势的两个联盟值相同或相差不大，例如，在任务分配问题中，根据不同的任务需要将员工分组，对于多数员工而言，被分配到哪一组区别并不大。因此，研究最优势结构生成问题具有很好的实际应用价值。

限界表示最坏情况下已搜索的局部最优解和全局最优解的距离。文[2]已经证明搜索联盟结构图的最底二层和顶层可以建立限界k＝n/2，这也表明限界k随着n的增大而增大。在这之后，若没有启发信息，应怎样进行进一步的部分搜索来降低限界k呢?文[3]最早提出一种以层为单位以最少的搜索层数达到给定限界要求的最优联盟结构生成算法。对于奇数限界k≥3，文[4]提出在搜索最底两层及顶层后，需要进一步搜索最大联盟的势大于或等于「n(k-1)/(k+1)⏋的所有联盟结构。文[5]提出了基于势结构的搜索算法，其在搜索最底两层及顶层后，只需进一步搜索CCS(n，k)所对应的的所有联盟结构。这三个算法[3-5]采用了不同的搜索单位，都可以用于势结构生成。

1 联盟结构与势结构

设n个agent的集合A＝{a1，a2，…，an}，联盟C是A的一个非空子集，联盟C中agent的个数称为联盟C的势。一个联盟结构CS是agent集的一个完全划分，称所有联盟结构的集合为M。设联盟结构 CS有 p个联盟 C1，C2，…Cp，且。令，，则把称为势结构(CCS)。6个agent的势结构图，如图1所示。

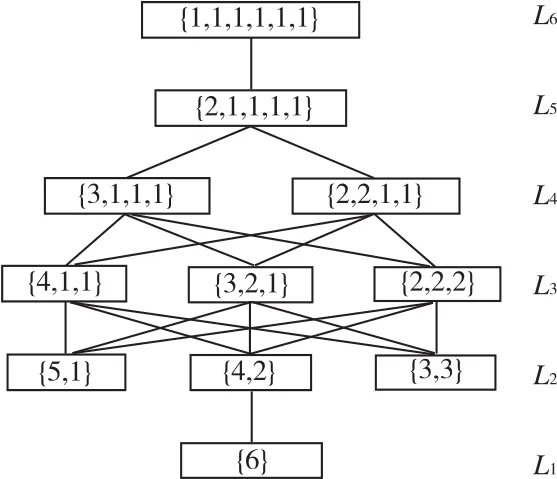
图1 6个agent的势结构图

表1 4个agent的势结构及其对应的联盟结构

在算法描述中，以势结构{n1，n2，…，np}为搜索单位，指的是搜索{n1，n2，…，np}所对应的所有联盟结构的集合。整数n的每一种划分对应一种势结构，例如正整数4有5种不同的划分，4个agent存在5个势结构，它们与15个可能的联盟结构的对应情况见表1。

2 势结构生成算法描述

定义1 取h＝⎿n/k」，余数m≡n mod k，显然m＜k。若m≥h，令CCS(n，k)＝∅，否则CCS(n，k)为满足以下条件的所有势结构集合[5]:

(1)若m＝0，令s＝n1+n2+…+ni，满足s≥h且s-ni＜h(ni≥2且ni+1＝1)；

(2)若m＝1，令s＝n1+n2+…+ni，满足s≥h且s-ni＜h(ni≥2且ni+1＝1)，另外CCS(n，k)还包含{h，1，…，1}势结构；

(3)若m≥2，令s＝n1+n2+…+ni，满足s≥h+1且s-ni＜h+1(n1＜h，ni≥2且 ni+1＝1)，另外 CCS (n，k)还包含{h，2，1，…，1}，…，{h，m，1，…，1}势结构。

例如:当n＝12，k＝3时，h＝4，m＝0；CCS (12，3)＝{{2，2，1，…，1}，{3，2，1，…，1}，{3，3，1，…，1}}；当n＝13，k＝3时，h＝4，m＝1；CCS (13，3)＝{{2，2，1，…，1}，{3，2，1，…，1}，{3，3，1，…，1}，{4，1，…，1}}；当n＝14，k＝3时，h＝4，m＝2；CCS(14，3)＝{{2，2，2，1，…，1}，{3，2，1，…，1}，{3，3，1，…，1}，{4，2，1，…，1}}。

算法描述如下:

Step 1 获得所要求的限界k，搜索联盟结构图的最底二层和顶层:L1，L2，Ln。若k≥「n/2⏋，转Step 3；若1≤k＜2，搜索整个联盟结构图，转Step 3；

Step 2 搜索势结构集合CCS(n，k)(若CCS (n，k)为空，k←k-1，直到CCS(n，k)不为空)对应的联盟结构；

Step 3 返回至今为止所得到的最优的联盟结构。

有以下结果:

定理1 对给定的限界k(2≤k≤「n/2⏋-1)，若算法2刚搜索完势结构集合CCS(n，k)(非空)对应的联盟结构，则限界为k。

3 算法改进

本节主要通过分析势结构生成算法中势结构间的关系，指出了该算法中一些可以去除的冗余搜索集合，从两个方面改进了算法，并进行了相关结果的证明。

3.1 算法的第一个改进

设agent个数为n，给定限界k，2≤k≤「n/2⏋-1，设V为任一给定的特征函数，记最优联盟结构CS∗＝{C1，C2，…，Ct}，已搜索过的最优联盟结构为CS∗N，若t≤k，记CS∗中值最大的联盟为C∗，则C∗在L1，L2中已搜索过，因此，

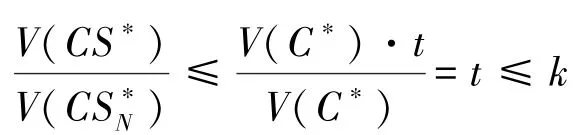
从而限界是k。

下面设t＞k，讨论算法的CCS(n，k)(参见第2节中定义1)中哪些势结构可以不搜，限界仍为k?

若CS∗中大小为1的联盟个数≥h，则它们分为一组；大小≥h的联盟每个单独分为一组。因此不失一般性，不妨假设CS∗中每个联盟的大小＜h，且联盟大小为1的联盟个数 ＜h，即h-1≥

定理2 设h＝⎿n/k」，m＝n mod k，当m＝0时，n＝kh，若ik＜h-i(i≥1)，则算法的CCS(n，k)中sub s≥2h-2i的势结构可以不搜，限界仍为k。

证明 CS∗中大小≥h-i的联盟每个单独分为一组，设有k1组，剩下的的联盟将满足s＝n1+n2+…+ ni，≥h且s-ni＜h(ni≥2且ni+1＝1)的联盟分为一组，这样的联盟组数为k2，每组的联盟大小之和≥h，余下的联盟(如果有的话)分成一组，这最后一组的联盟大小之和记为m∗，显然m∗＜h。这k1+k2组中除了符合定理5所提条件的组不搜索外，其他每一组已被搜索过。

若k1＝0或m∗＝0，则n＝kh≥k2h+m∗，从而k2≤k，且若k2＝k，则m∗＝0，这样n最多分成k组，限界为k。

若k1≠0且m∗≠0，由ik＜h-i，有

(k+1)(h-i)＞n＝kh≥k1(h-i)+k2h+m∗≥(k1+k2)(h-i)+m∗。

由(k+1)(h-i)＞(k1+k2)(h-i)+m∗，得k1+k2＜k+1，即有k1+k2≤k。

若k1+k2＜k，则总共不超过k组，限界为k，下设k1+k2＝k，有(k+1)(h-i)＞k(h-i)+m∗，即m∗＜h-i。

取k1组中的最后一组联盟，记为，则该组可与最后余下的联盟大小之和为m∗的组合并为一组，这新的一组联盟大小之和＜2h-2i，已被搜索过。否则，若，则有

当m≠0时，算法3的CCS(n，k)中哪些势结构可以不搜，存在与定理2类似的结论，由此得出以下定理3。

定理3 设h＝⎿n/k」，m＝n mod k，当0≤m＜h时，对于算法中的CCS(n，k)，令sub s＝n1+n2，则当ik＜h-i-m-1时，sub s≥2h-2i-1的势结构可以不搜，限界仍为k；否则，当ik＜h-i-m时，sub s≥2h-2i的势结构可以不搜，限界仍为k。

不妨设t＞k，h＝⎿n/k」，m＝n mod k，n＝k·h+ m，我们希望将CS∗中的t个联盟分成至多k个组合，使每个组合均已搜索过，这样限界就会≤k。证明过程类似于定理2，这里不再说明。

注意到，只要k＞0(实际上我们讨论的是k≥2)，当ik+m＜h-i-1时，一定满足ik+m＜h-i；对较小的i上式成立，则对较大的i上式也成立。举例来说，当满足3k＜h-4时，一定满足2k＜h-3，k＜h-2，3k＜h-3，2k＜h-2和k＜h-1，因此，应取满足条件的最大的i值。

例如 当n＝50，k＝2时，h＝⎿50/2」＝25，m＝0，满足8k＜h-8，不满足8k＜h-9和9k＜h-9，算法的CCS(50，2)所包含的势结构中sub s≥2h-16＝34的势结构都可以不搜，即共64个势结构{24，24，1，…，1}，…，{24，10，1，…，1}，{23，23，1，…，1}，…，{23，11，1，…，1}，{22，22，1，…，1}，…，{22，12，1，…，1}，{21，21，1，…，1}，…，{21，13，1，…，1}，{20，20，1，…，1}，…，{20，14，1，…，1}，{19，19，1，…，1}，…，{19，15，1，…，1}，{18，18，1，…，1}，…，{18，16，1…，1}，{17，17，1…，1}无须搜。

3.2 算法的第二个改进

给出n，k，h＝⎿n/k」，余数m＜k。 情况1:m≥h时，苏射雄等人的算法为避免讨论这种情况，令CCS(n，k)＝∅，接着讨论下一个较小的k(k从「n/2⏋-1到2)。当k变小，h＝⎿n/k」变大，逐步降低k，这可使得m＜h，变成情况2:m＜h。例如:当n＝100，k＝32时，h＝⎿100/32」＝3，m＝4，有m＞h，k从32逐次降到26时，h＝3，m＝22，CCS(n，k)均为空集，直到k＝25，h＝4，m＝0。

为使对k的调整一次到位，对情况1:m≥h，我们改进如下:取h∗＝「n/k⏋，搜相应的CCS∗(n，k)，这时得到的限界为「n/h∗⏋不大于原来的k。例如:当n＝100，k＝32时，由于m≥h，取h∗＝「100/32⏋＝4，搜相应的CCS∗(n，k)后，得到的限界k＝「100/4⏋＝25(小于给出的k＝32)，这样可以一步调整到位。 又如:当n＝120，k＝11时，h＝「120/11⏋＝10，m＝10，有m＝h，CCS(n，k)为空集，当原算法k从11降到10时，h＝12，m＝0，搜相应的CCS∗(n，k)，达到限界k＝10，这也表明原算法对k＝11没有给出解。这时我们改进的算法取h∗＝「n/k⏋＝「120/11⏋＝11，搜相应的CCS∗(n，k)之后得到的限界k＝「n/h∗⏋＝「120/11⏋＝11(和所要求的限界k一样)，这样就给出了k＝11时的解，这样就改进了原算法当m≥h时的不足:原算法CCS(n，k)为空集，无直接解。

4 相关算法的比较

对于给定的较小的限界要求k，算法在搜索完L1，L2和Ln层后，需要进一步搜索的势结构数的比较数据示例如下:

当n＝50，k＝3时，文[2]的算法需要搜索第28至49层共4507个势结构所对应的联盟结构数。文[3]的算法需要搜索第28层共1002个势结构所对应的联盟结构数。文[4]的算法需要搜索最大联盟的势≥25的9296个势结构所对应的联盟结构数。文[5]的算法需要搜索257个势结构数，它们所对应的联盟结构数为 s＝4488694148454579188284988，lg s＝24.6521。而改进后的算法减少的12个势结构为{15，15，1，…，1}，{15，14，1，…，1}，{15，13，1，…，1}，{15，12，1，…，1}，{15，11，1，…，1}，{15，10，1，…，1}，{14，14，1，…，1}，{14，13，1，…，1}，{14，12，1，…，1}，{14，11，1，…，1}，{13，13，1，…，1}，{13，12，1，…，1}，这些势结构对应的联盟结构数为 s＝14236151842773330300000，lg s＝22.153393。

当n＝50，k＝2时，改进后的算法减少的64个势结构分别为{24，24，1，…，1}，…，{24，10，1，…，1}，{23，23，1，…，1}，…，{23，11，1，…，1}，{22，22，1，…，1}，…，{22，12，1，…，1}，{21，21，1，…，1}，…，{21，13，1，…，1}，{20，20，1，…，1}，…，{20，14，1，…，1}，{19，19，1，…，1}，…，{19，15，1，…，1}，{18，18，1，…，1}，…，{18，16，1…，1}，{17，17，1…，1}，这些势结构对应的联盟结构数为s＝90145645776100288100000，lg s＝22.954945，而原算法需搜索的联盟结构数为 s＝340283128981380143981052949884594687517，lg s＝38.5318。当n＝100，k＝2时，改进后的算法减少了272个势结构，这里不再一一列出。

5 结语

在分布式传感器网络中，多个传感器可以组成联盟以共同跟踪感兴趣的目标。最优联盟结构生成是联盟形成中的一个关键问题。近年来，势结构生成算法[6]的研究工作有了一定进展。本文深刻分析了势结构间的关系，并论证了如何去除一些冗余的搜索，从两个方面提出对文[5]中算法的改进，进一步完善了文[3]和[5]的算法对于m≥h情况的解，并给出相关结果的证明具有很好的理论意义和实用价值。今后的工作拟在已有成果的基础上，进一步探讨算法所构造的势结构是否冗余，势结构每个所对应的全部联盟结构是否都必须搜索，并且可以尝试将势结构的有关算法思想应用到组合拍卖、网格计算等实际应用中，并考察除层和势结构外，是否可以构造更小的搜索单位优化现有联盟结构生成算法，使所搜索的联盟结构数进一步减少。也可以研究如何利用给定联盟值[7-8]减少搜索空间，或者考虑引入群智能算法(遗传算法、蚁群算法、粒子群算法等)来求解次优联盟结构[9-10]。

[1]谢辉斯.基于组合拍卖处置我国国有银行不良资产的研究[D].重庆:重庆师范大学，2013.

[2]Sandholm TW，Larson K，Andersson M，et al.Coalition structure generation with worst case guarantees[J].Artificial Intelligence，1999，111(1-2):209-238.

[3]胡山立，石纯一.给定限界要求的联盟结构生成[J].计算机学报，2001，24(11):1285-1290.

[4]Dang V D，Jennings N R.Generating coalition structures with finite bound from the optimal guarantees[C]//In Proceedings of the 3rd International Joint Conference on Autonomous Agents and Multi-Agent Systems(AAMAS2004)，New York，USA，564-571.

[5]SU Shexiong，HU Shanli，ZHENG Shengfu，et al.Coalition structure generation with given required bound based on cardinality structure[C]//In Proceedings of the 6th International Conference on Machine Learning and Cybernetics in Hong Kong，Hong Kong. 2007:2505-2510.

[6]李少芳，胡山立，石纯一.一种基于势结构分组思想的任一时间联盟结构生成[J].计算机研究与发展，2011，48(11):2047-2054.

[7]刘惊雷，张伟，刘兆伟，等.联盟结构图的性质及应用[J].计算机研究与发展，2011，48(4):602-609.

[8]Rahwan T，Jennings N R.An algorithm for distributing coalitional value calculations among cooperating agents[J].Artificial Intelligence，2007，171(8/9):535-567.

[9]Rahwan T，Ramchurn SD，Dang V D，et al.Near-optimal anytime coalition structure generation[C]//Proc of the 20th Int Joint Conf on Artificial Intelligence(IJCAI2007).San Francisco:Morgan Kaufmann，2007:2365-2371.

[10]Tang，P.and Sandholm，T.Approximating Optimal Combinatorial Auctions for Complements Using Restricted Welfare Maximization [C]//In Proceedings of the International Joint Conference on Artificial Intelligence(IJCAI)，2011.

(责任编辑:曾 晶)

Im provement of Cardinality Structure Generation Algorithm w ith Given Required Bound

LIShao fang∗，CHE Yan

(College of Information Engineering，Putian University，Putian 351100，China)

Finding the optimal coalition structure is NP-complete.Theminimal search that can establish a bound k＝n/2 is searching the lowest two levels and the top level of the coalition structure graph.Afterminimal search，different algorithms adopt the different search units and path tomake selectively part search，as soon as possible to achieve a given bound value.In practice，making full use of the characters of the same or similar value in two coalitionswith the same cardinality to study themost optimal cardinality structure generation to improve algorithm efficiency.The paper analyzes the relations between cardinality structures，and points out some redundancy search set than can be removed in cardinality structure generation algorithm with given required bound，improves the algorithm from two aspects and proves the related result.

cardinality structure(CCS)；given required bound；multi-agents system；algorithm improvement

TP18

A

1000-5269(2016)04-0069-05

10.15958/j.cnki.gdxbzrb.2016.04.14

2015-10-24

福建省教育厅资助项目(JA15440)

李少芳(1971-)，女，副教授，硕士，研究方向:计算机算法，人工智能应用基础，多agent系统，Email:LSF9808＠163.com.

∗通讯作者:李少芳，Email:LSF9808＠163.com.