非线性各向异性介质中TE波的色散特性
2016-12-19赵海军
王 洋,赵海军
(西华师范大学 计算机学院,四川 南充 637009)
非线性各向异性介质中TE波的色散特性
王 洋,赵海军
(西华师范大学 计算机学院,四川 南充 637009)
非线性异向介质中的电磁波传播一直都是人们重点关注的问题.该文主要研究了非线性各向异性介质中TE波传播的色散特性.为此,首先从麦克斯韦方程组出发,得到了非线性异向介质中TE波传播常数所满足的特征方程,然后利用辐射条件和传播条件,并通过解析,把该问题的麦克斯韦方程组简化成了非线性边值问题,从而得到了传播特性所满足的色散方程;仿真表明,由色散方程所给出的色散曲线能够很好地刻画非线性异向介质中TE波的传播特性.
非线性特性;各向异性;传播常数;色散;边值问题
从20世纪70年代至今,非线性波导结构中的电磁波传播问题得到了广泛研究[1-4].文献[5]针对具有克尔非线性特性的单层圆柱形波导中的电磁波传播问题给出了严格的电磁场表达式;文献[2,3]还解决了具有克尔非线性特性的多层媒质层中的TE波和TM波的传播问题;文献[6]对具有克尔非线性特性的异向介质中的TE波传播问题进行了研究,并给出了一些数值结果,文献[3-8]针对非线性多层媒质和非线性异向介质中的TM波传播问题进行了研究;文献[9]对各向异性导体-介质-等离子体特殊多层结构中电磁波的传播特性进行了研究,得到了该结构中的色散方程,分析了金属网角度、介质厚度和介电常数对色散的影响;文献[10]针对多分层介质中平面电磁波的传播特性,用波阻抗法和等效传输原理计算出了各层介质的反射系数和透射系数的理论公式.本文针对任意非线性异向介质中的TE波的传播问题进行研究,得到了色散方程和传播常数.
2 任意非线性异向介质中的TE波传播问题
2.1 问题的导出
首先考虑均匀、各向同性、无磁介质的媒质层中的电磁波传播.设x<0和x>h的两个半空间充满了均匀、各向同性、无磁介质的媒质,且没有任何场源,介电常数分别为ε1≥ε0和ε3≥ε0(ε0为自由空间的介电常数),都有μ=μ0(μ0为自由空间的磁导率),如图1所示.
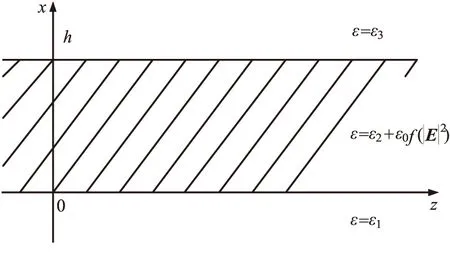
图1 问题的几何表示
设电磁场为时谐场:
式中ω为角频率,E+,E-,H+,H-为空间变量x,y,z的实函数.根据时谐场的复数表示法,省略时间变量,表达式E=E++jE-,H=H++jH-为复振幅,且E=(Ex,Ey,Ez)T,H=(Hx,Hy,Hz)T.
电磁场E,H满足麦克斯韦方程组:
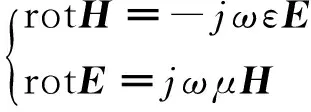
(1)
在媒质界面x=0和x=h处满足切向场分量连续性条件和在无穷远满足辐射条件:即在x<0和x>h区域,当|x|→∞时,电磁场按指数规律衰减.
设f为解析函数,0
2.2 任意非线性异向介质中的TE波
考虑TE波E=(0,Ey,0)T,H=(Hx,0,Hz)T,其中电磁场分量Ey,Hx,Hz与变量y无关,沿媒质界面传播的电磁波为z的时谐波,意味着分量有形式Ey=Ey(x)ejγz,Hx=Hx(x)ejγz,Hz=Hz(x)ejγz,这样可从方程组(1)得到:
γ2Ey(x)-E″y(x)=ω2μεEy(x)
(2)
式中(·)′≡d/dx,γ为未知的传播常数.
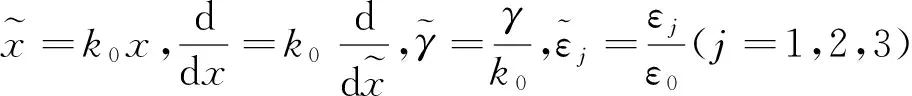
Y″(x)=γ2Y(x)-εY(x)
(3)
引入新函数Z(x)=Y′(x),于是式(3)可看成下列方程组:
(4)
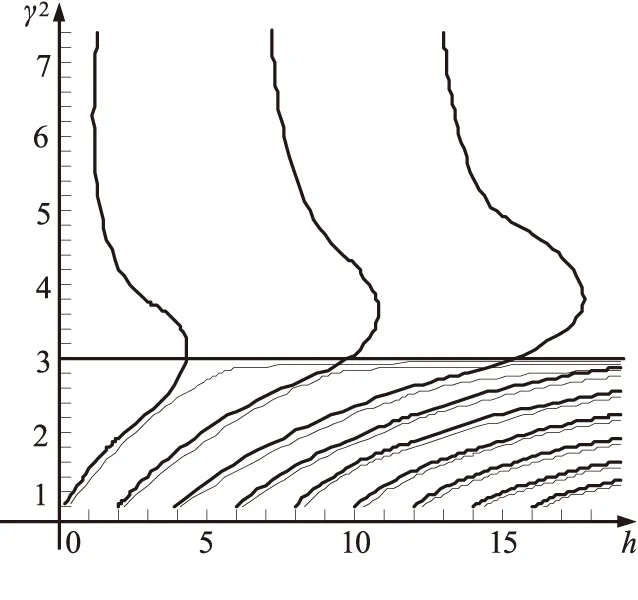
于是问题变成寻找沿0 2.3 解微分方程组(4) 在区域x<0有ε=ε1,根据辐射条件,可得到方程组(4)的解为: (5) 式(5)中γ2-ε1>0,否则就不能满足辐射条件. 在区域x>h有ε=ε3,根据辐射条件,可得到方程组(4)的解为: (6) 同样,式(6)中γ2-ε3>0. 方程组(5)、(6)中的常数A、B由传播条件和初始条件确定. 在区域0 (7) 方程组(7)有第一积分,用方程组(7)中第二个方程除以第一个方程,就得到全微分方程ZdZ+(ε2-γ2+f(Y2))YdY=0,它的通解为: Z2+(ε2-γ2)Y2+φ(Y2)=C (8) 式中φ(Y2)=∫f(u)du|u=Y2,C为积分常数. 由此可见,函数Y(x)、Z(x)的传播条件为: (9) 这里: [f]x=x0=limx→x0-0f(x)-limx→x0+0f(x) 在半空间x<0和ε=ε1有: (10) 在0 L(F,γ)≡DF-G(F,γ)=0 (11) 在半空间x>h和ε=ε3有: (12) 根据传播条件(9)和第一积分式(8)可得到关于Y0的方程: (ε2-ε3)Yh2+φ(Yh2)=(ε2-ε1)Y02+φ(Y02) (13) 于是问题就归结为:寻找本征值γ和对应于这些本征值的非零向量F,以使F满足式(10)-(12),向量F的分量满足传播条件(9),Y(0)≡Y0由式(13)确定. 定义1:在条件(9)和(13)下,使得问题(10)-(12)的非零解F存在的γ=γ0称为问题的本征值.对应于这个本征值的解F称为问题的本征向量,向量F的分量Y(x)和Z(x)称作本征函数. 记τ(x)=ε2+Y2(x),η(x)=Z(x)/Y(x),于是方程组(7)有形式: (14) 第一积分式(8)有形式: (τ-ε2)η2+(ε2-γ2)(τ-ε2)+ φ(τ-ε2)=C (15) 如果非线性函数f是一个多项式,则式(15)就是一个关于τ的代数方程.麦克斯韦方程组中的本构关系中的极化向量就可以用|E|展开为级数.截取这个级数就得到一个多项式函数. 此外,还有τ(0)=ε2+Y02,τ(h)=ε2+Yh2,由于Yh已知,故τ(h)已知,根据传播条件,可得到η(0)和η(h): (16) 代入x=h到式(15),得到: Chτ=C|x=h= (ε2-ε3)(τ(h)-ε2)+φ(τ(h)-ε2) 结合式(15),利用式(16)和Chτ,可以得到关于τ(0)的方程为: (τ(0)-ε2)(ε2-ε1)+φ(τ(0)-ε2)= (ε2-ε3)(τ(h)-ε2)+φ(τ(h)-ε2) (17) 显然,τ(0)≥ε2,因为τ(0)=ε2+Y02且ε2>0.式(17)存在根τ(0)≥ε2,必须对函数f附加某些条件,如f为非负系数的多项式函数,则根存在. 值得注意的是,从式(17)可见,如果ε1=ε3,则方程有一个根是τ(h),也就是τ(0)=τ(h).采用原来的变量,就得到Y02=Yh2.对线性媒质层来说,情况几乎相同,只是有一个微小差别,即在线性情况下,当ε1=ε3时,总有Y02=Yh2,在非线性情况下,式(17)仅有一个根. 假设函数f满足条件(γ2-ε2-f(τ-ε2)-η2)<0,事实上如果f是一个非负系数的多项式函数,这个条件的确是成立的.在这种情况下,方程组(14)的第二个方程的右边就是负的,这意味着当x∈(0,h),函数η就减小,从式(16)可以看到η(0)>0,η(h)<0,但函数Y有可能为零,因为Y和Z为解析函数,对η来说也是这样.这就意味着对于Y=0,η有第二类间断点,这些点是函数η的极点. 从第一积分式(15)有: 极点就是这个表达式分母为零,即在这些极点τ*=τ(x*),η*=±∞. 假设在区间x∈(0,h)存在N+1个间断点x0,…,xN,对函数η=η(x)来说,意味着η(xi-0)=-∞,η(xi+0)=+∞,i=0,…,N. J(γ,H)= (18) 式中N≥0为整数,方程对任意有限的h都是成立的,对于不同的N(N≠0)有不同的色散方程,必须解关于γ的每个方程. 定理1:色散方程式(18)的解集包含具有边界条件(9)、(13)的边值问题(10)-(12)的解集(本征值). 定理2:如果式(18)有唯一解τ(0)≥ε2,则具有边界条件(9)和(13)的边值问题(10)-(12)有一个解(本征值)当且仅当这个本征值是色散方程式(18)的一个解. 令: inf和sup分别表示下界和上界,则有下面的定理3. 还可以证明,对于任意实数值ε2和max(ε1,ε3)<γ2<+∞,色散方程有式(18),N=0,±1,±2,…. 必须强调的是,这种非线性问题本质上依赖于初始条件Yh,而对于线性媒质来说,传播问题不依赖于初始条件. 图2所示为仿真得到的色散曲线变化情况.仿真中采用的非线性函数f=aY2+bY4+cY6+dY8,a,b,c,d取2组不同的值,ε1=ε3=1,ε2=3,Yh=1.虚线为线性媒质(即f≡0)的色散曲线,γ2=3的直线为线性情况下的渐近线,实线为非线性情况下的色散曲线(即式(18)的解). 从仿真结果可见,当f>0时,由式(18)定义的函数h≡h(γ)有limγ2→+∞h(γ)=0.这意味着在非线性情况下,色散曲线总有一条渐近线h=0.从图(2b)可见,直线h=13对应媒质层的厚度,对于线性媒质来说,这时有7个传播常数(直线h=13与7条色散曲线(细线)相交的6个点),这些传播常数就是对应于本征模的本征值;对于非线性媒质来说,有5个本征值(即图2(b)即h=13与5条色散曲线(粗线)相交的4个点),这些本征值对应4个本征模. (a)a=b=c=d=0.05 (b)a=0.05,b=c=d=0.005 总之,在线性和非线性情况下,存在很大的差别.在非线性情况下,有无穷多个本征模,而在线性情况下,本征模数量总是有限的,而且在线性情况下,在区间ε2<γ2<+∞不存在本征值. [1]Shurmann,H.W.,V.S.Serov,Y.V.Shestopalov.TE-polarized waves guided by a lossless nonlinear three-layer structure[J].Physical Review E,1998,58(1):1040-1050. [2]Valovik,D.V.,Y.G.Smirnov.Calculation of the propagation constants of TM electromagnetic waves in a nonlinear layer[J].Journal of Communications Technology and Electronics,2008,53(8):883-889. [3]Joseph,R.I.,D.N.Christodoulides.Exact field decomposition for TM waves in nonlinear media[J].Optics Letters,1987,12(10):826-828. [4]Leung,K.M..Scattering of transverse-magnetic waves with a nonlinear film:Formal field solutions solutions in quadratures[J].Physical Review B,1991,44(10):5007-5012. [5]Eleonskii,P.N.,L.G.Oganes'ants,V.P.Silin.Cylindrical nonlinear waveguides[J].Sov.Phys.JETP,1972,35(1):44-47. [6]Valovik,D.V..Propagation of electromagnetic waves in a nonlinear metamaterial layer[J].Journal of Communications Technology and Electronics,2011,56(5):544-556. [7]Valovik,D.V.,Y.G.Smirnov.Calculation of the propagation constants and fields of polarized electromagnetic TM waves in a nonlinear anysotropic layer[J].Journal of Communications Technology and Electronics,2009,54(4):391-398. [8]Valovik,D.V.,Y.G.Smirnov.Nonlinear effects in the problem of propagation of TM electromagnetic waves in a Kerr nonlinear layer[J].Journal of Communications Technology and Electronics,2011,56(3):283-288. [9]吴振华,张开春,刘盛纲.特殊多层结构中电磁波传播特性研究[J].电子科技大学学报,2010,39(4):505-508. [10]马如慧,刘生春.多分层介质中平面电磁波的传播特性分析[J].现代电子技术,2008,282(19):36-38. (责任编辑:王前) 10.13877/j.cnki.cn22-1284.2016.08.025 2016-04-10 四川省科技厅支撑项目(2014SZ0104);西华师范大学基本科研业务费专项资金资助项目(14C002) 王洋,男,四川西充人,西华师范大学计算机学院硕士研究生;赵海军,男, 四川广安人,教授,硕士导师. TP393.17 A 1008-7974(2016)04-0076-04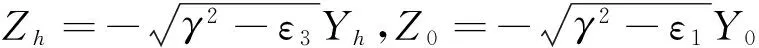
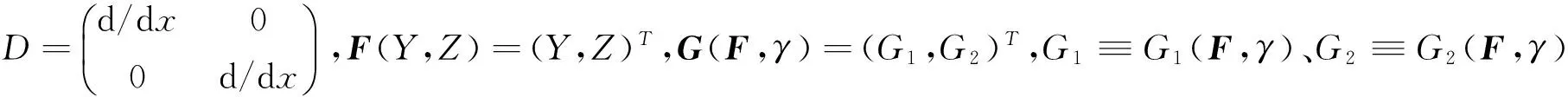
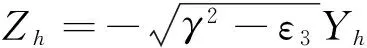
3 色散方程
4 仿真

5 结论
