基于Landsat 8-OLI的荒漠化地区植被覆盖度反演模型研究
2016-12-19马中刚王广兴佘宇晨
马中刚 ,孙 华 ,王广兴 ,2,林 辉 ,佘宇晨 ,邹 琪
(1.中南林业科技大学 林业遥感信息工程研究中心,湖南 长沙 410004; 2. Dept. of Geography, Southern Illinois University, USA)
基于Landsat 8-OLI的荒漠化地区植被覆盖度反演模型研究
马中刚1,孙 华1,王广兴1,2,林 辉1,佘宇晨1,邹 琪1
(1.中南林业科技大学 林业遥感信息工程研究中心,湖南 长沙 410004; 2. Dept. of Geography, Southern Illinois University, USA)
基于Landsat 8-OLI影像数据,利用植被指数逐步回归分析和线性混合像元分解的方法,结合134个野外样地调查数据,将线性混合像元分解结果(植被丰度)导入影像植被指数逐步回归模型,建立康保县荒漠化地区植被覆盖度反演混合模型,并进行精度检验。结果表明:(1)在所选16种影像植被指数中,采用单一植被指数进行荒漠化地区植被覆盖度反演建模,与植被覆盖度拟合优度最高的是归一化植被指数(NDVI)和土壤调节植被指数(SAVI),利用植被指数逐步回归分析建模,筛选出的3种最佳影像植被指数是土壤调节植被指数(SAVI0.5),比值植被指数(SRN-R)和增强型植被指数(EVI);(2)通过线性混合像元分解建立的植被覆盖度反演模型,分解所得植被丰度与植被覆盖度的决定系数为0.673,模型精度低于利用植被指数逐步回归分析法反演的模型精度,但高于单一植被指数与植被覆盖度反演模型的精度;(3)精度检验显示植被指数逐步回归分析法反演的植被覆盖度模型的决定系数(R2)和精度分别为0.719和86.70%,而混合像元分解和植被指数逐步回归分析综合所建的混合模型的决定系数(R2)和精度分别为0.807和92.37%,表明植被指数逐步回归分析与混合像元分解相结合能较好地提高荒漠化地区植被覆盖度反演精度。
荒漠化;植被覆盖度反演;影像植被指数;逐步回归分析;线性混合像元分解
土地荒漠化是指由于气候变化和人类不合理的经济活动等因素,使干旱、半干旱和具有干旱灾害的半湿润地区的土地发生了退化[1-2]。它使土地资源数量不断减少,沙尘暴等自然灾害频繁发生,生态环境逐渐恶化,严重影响区域生态环境和经济的可持续发展[3-4]。因此,发展一个精确的土地荒漠化监测和预估模型,为土地荒漠化防治提出科学、准确的理论与方法具有重要的理论意义与实用价值。
随着航空航天技术的发展,建立基于遥感影像的植被覆盖度预测模型已成为荒漠化监测与评价的主要手段[5-7]。常用的遥感反演植被覆盖度方法主要有经验模型法和混合像元分解模型法。前者是建立影像植被指数(如NDVI)与植被覆盖度之间的回归关系估算植被覆盖度;后者是基于影像中的一个像元有多个组分构成,并对该像元的信息都有贡献,用数学模拟方法将信息分解,得到各组分丰度,从而估算植被覆盖度[8]。如,Xiao等[9]用Landsat ETM+ NDVI图像和线性回归方法完成了植被覆盖度的估算;马超飞等[10]利用线性混合像元分解从Landsat ETM+影像中提出了像元的植被覆盖度。干旱荒漠化地区植被分布稀疏,混合像元现象突出,而从遥感影像上监测到的植被光谱信息较为微弱,纯净端元的选取也较为困难,从而影响反演精度[11]。因此,在干旱荒漠化地区采用单一的植被指数回归或混合像元分解法建立植被覆盖度反演模型,其精度常常无法满足要求。本研究采用了基于植被指数的逐步回归与混合像元分解相结合的方法,建立一个荒漠化地区植被覆盖度的混合模型,以提高荒漠化地区植被覆盖度的估计精度,为预测荒漠化地区植被覆盖度提供理论依据和技术支撑。
1 研究区概况
康保县地处河北省西北部,隶属于张家口市。东、北、西三面分别与内蒙古自治区的太仆寺旗、正镶白旗、化德县、商都县接壤,南部同张北、沽源、尚义三县毗邻,总面积3 365 km2。地势由东北向西南缓缓倾斜,北部、东部为丘陵区,南部为波状平原区,平均海拔1 450 m,地理坐标为东经 114°11′~ 114°56′,北纬 41°25′~ 42°08′,属东亚大陆性季风气候中温带亚干旱区,雨热同期,年均气温1.2℃(见图1)。
2 材料与方法
2.1 影像数据获取与处理
研究所使用的遥感数据为美国陆地卫星Landsat 8-OLI,接收时间为2014年8月1日,共有11个波段。本次研究选取前7个空间分辨率30 m×30 m的多光谱波段和第8个空间分辨率15 m×15 m的全色波段。首先将影像的原始灰度(DN)值转换为大气外层表面反射率,消除传感器本身产生的误差。然后,完成大气校正,消除大气和光照等因素对地物反射的影响,获得地物反射率。最后,将低空间分辨率的多光谱图像与高空间分辨率的单波段黑白影像重采样生成一幅高分辨率多光谱图像,便于端元选择,从而提高混合像元分解精度。数据处理前后的影像见图2(封三)。
2.2 样地调查与数据处理
研究对土地荒漠化(康保县)地区开展系统抽样,共布设样地134个,实际调查了 124个样地(不含水域和建设用地)。样地设计确定抽样间隔为5 km×5 km,样地大小设置为30 m×30 m。考虑到与本研究Landsat 8影像的匹配性(影像融合后空间分辨率为15 m×15 m),在样地中心点及两对角线水平方向上7.5 m处选择一个1 m×1 m的样方进行调查。在每个小样方内,用皮尺在样方的东西和南北方向测量样方的植被覆盖度,以10 cm为间隔查看是否有植被覆盖,取两次测量的均值作为样方的植被覆盖度,同时测量植被高度。然后,用三角架支撑的数码相机拍照,以便由数码照片计算植被覆盖度。
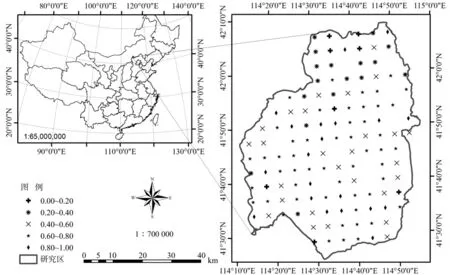
图1 研究区地理位置及样地分布Fig.1 Geographic location of the study area
除了样地野外调查之外,植被覆盖度也可由数码照片分类获得。即根据照片中不同植被类别和不同颜色的数据化(DN)值,探求数码照片可见光波段R、G、B对不同的地物所显现的DN值(0~255)的不同组合规律,进行决策树分类得到植被覆盖度。图3(a)显示了这两种方法所得的样地植被覆盖度。因为荒漠化地区植被稀疏且分布随机性大,所以以10 cm为间隔,通过外业测量所得的植被覆盖度较地面样地真实植被覆盖度易偏大,而通过数码照片提取的植被覆盖度由于地面阴影等因素的存在较样地真实植被覆盖度易偏小。但二者之间具有良好的线性关系(见图3b),决定系数(R2)为0.808。

图3 实地调查与影像植被覆盖度Fig.3 Field survey and image extraction coverage
2.3 植被指数的提取
研究共选取了归一化植被指数(NDVI)、比值植被指数(SR)、土壤调节植被指数(SAVI)、增强型植被指数(EVI)、大气阻抗植被指数(ARVI)、差值植被指数(DVI)及衍生植被指数。其中,SR和DVI通过选取近红外和可见光各波段组合共有8种(如近红外与红色波段比值植被指数表示为SRN-R,近红外与海蓝波段差值植被指数表示为DVIN-C),SAVI根据其调节因子(0.1、0.2、0.3、0.4、0.5)有5种,实际共计算了16个指数因子[12]。利用ENVI软件的BAND MATH工具进行提取。
2.4 植被覆盖度反演方法
2.4.1 逐步回归
本研究采用逐步回归分析进行自变量的筛选,以保证所有入选回归方程的自变量是最优且显著性是最高的[13]。首先,对所有16种植被指数与植被覆盖度单独拟合建立覆盖度反演模型,获得反演植被覆盖度的最优植被指数;其次,分析植被指数与植被覆盖度的相关性,通过共线性诊断移除相关性较高的变量,再利用逐步回归分析筛选出最终植被指数建立模型。同时,对124个野外调查样地数据进行残差分析,剔除5个离群值大的数据。然后,随机选取90个样地进行建模,将剩余的29个样地用于精度检验。
2.4.2 线性混合像元分解与逐步回归的综合
混合像元分解主要可分为线性和非线性方法。非线性比线性混合像元分解更复杂,且所得结果难以直观解释,使得准确定量反演植被覆盖度较为困难[14-16]。因此,本研究采用线性混合像元分解进行植被覆盖度反演。该方法是假设像元内部各组分对像元信息都有贡献,但没有交互作用,以各组分的光谱特征值为因子,它们面积为权重,建立线性混合模型:

式中:Rj为波段j的各像元反射率;fi为端元i在混合像元中所占的比例;rij为端元i在波段j中的反射率;n为端元的个数;ej为拟合波段j的误差。已知混合像元和各端元的值,通过最小二乘法可以求解出各组分在混合像元中的比例,即植被覆盖度。本研究选取植被、裸露地和水体3个端元,用Landsat 8-OLI影像进行线性混合像元分解。
端元的合理选取影响着分解的精度[17-18]。通常可用几何顶点(N-FINDA)和纯净像元指数(PPI)两种方法来完成端元选取。后者对像元纯度要求高,而荒漠化地区植被稀疏且分布随机性大,纯度高的像元较少,端元选取受到很大的影响,从而降低混合像元分解的精度。相比之下,基于几何顶点的端元选取每个顶点都是一种地物类型且具有明确的物理意义,还能通过目视解译和影像交互进行分析选取,因此基于几何顶点的方法更适合于荒漠化地区端元选取。该方法是先将影像进行最小噪声分离(MNF)变换,去除波段间的相关性,再将MNF变换结果前面两个相关性很小的波段作为X、Y轴构成二维散点图。其散点图一般是三角形状,纯净端元的位置分布在三角形的三个顶点,其内部的点则是这三个顶点的线性组合,也就是混合像元。本研究将混合像元分解得到的植被分量作为一个变量导入到逐步回归分析所得的最佳模型中,再次进行植被覆盖度反演。
2.5 精度检验
利用29个未参与建模的样地数据对以上逐步回归植被覆盖度反演模型和逐步回归分析与线性混合像元分解综合建立的混合模型进行精度检验,其选用包括决定系数(R2)、均方根误差(RMSE)和相对误差(RE%)。
3 结果与分析
3.1 植被指数与植被覆盖度相关性分析
研究对所选取的16种植被指数分别进行了线性回归建模,结果NDVI与SAVI0.1-0.5所得植被覆盖度回归模型的决定系数(R2)为最高(0.604),ARVI的决定系数(R2)为最低(0.356)。对SAVI来看,土壤调节因子L对荒漠化地区SAVI与植被覆盖度线性回归模型基本没有影响。经研究分析造成该现象的可能原因有两点:一是因为研究区域较小,区域内土壤覆盖类型有限,不同土壤类型光谱差异不大,像元光谱变化主要取决于植被光谱信息,土壤调节因子起不到相应的作用;二是也有研究指出土壤调节因子L考虑的是通过冠层时的红光和近红外消光差异,随植被密度的变化而变化,影响较大的区域是中等植被覆盖度地区,而不是植被非常稀少的干旱荒漠化地区。
3.2 逐步回归分析建模
利用逐步回归进行自变量的筛选和建立植被覆盖度反演模型,其结果见表1。最先引入回归方程的自变量为土壤调节植被指数SAVI0.5,然后是SRN-R和EVI。随着模型中变量的增加,R2、修正的R2随之增大,估计标准误差随之减少。最终得到的模型包括了3个显著的植被指数(SAVI0.5,SRN-R和EVI),估计标准误差为0.132。变量回归系数见表2。将表2中“非标准化回归系数”栏目中的值代入多元回归模型得到最优的逐步回归模型(方程2)。

表1 逐步回归拟合结果Table 1 Results of stepwise regression

表2 逐步回归最终模型参数估计值统计Table 2 The statistics of stepwise regression models

3.3 线性混合像元分解植被覆盖度反演模型
在二维散点图中根据三角形三个顶点对应于影像上的地物类型选择端元,然后将选取的端元输入N维可视化器进行可分离性检验,最终确定用于混合像元分解的端元并进行线性混合像元分解,得到的植被和裸地丰度图(如图4所示)。将植被丰度图输入ArcGIS空间分析模块中,提取对应样本点的数据信息,并与植被覆盖度进行相关性分析(如图5所示)。
由图5可知,线性混合像元分解对植被覆盖度的决定系数(R2)为0.673,比单个植被指数回归反演的植被覆盖度模型决定系数(R2= 0.604)高,却比通过植被指数逐步回归反演植被覆盖度决定系数(R2= 0.748)低。说明在植被稀疏的荒漠化地区,线性混合像元分解反演植被覆盖度优于单一植被指数的植被覆盖度反演,却不及植被指数逐步回归植被覆盖度反演。

图4 线性混合像元分解结果Fig. 4 Results of linear unmixing analysis

图5 线性混合像元分解结果与样地植被覆盖度相关性Fig.5 Relationship of vegetation fraction values from linear unmixing analysis with fi eld observations of sample plots
3.4 逐步回归分析和线性混合像元分解综合建模
把混合像元分解结果(植被丰度)作为自变量导入到植被指数最佳回归模型中,再利用SPSS软件分析得出反演研究区植被覆盖度的混合模型,其与植被覆盖度的决定系数(R2)为0.807,估计标准误差为0.123。混合模型为:

4 模型精度检验
利用剩余的29个样地数据对植被所获植被覆盖度反演模型进行精度检验,结果如表3和图6所示。以SAVI0.5、SRN-R、EVI和Vegetation fraction(Vegfrac)这4个因子建立的混合模型估测值与植被覆盖度实测值拟合优度较高,其判定系数(R2)为0.8,均方根误差为0.1631,相对误差为7.63%,即模型精度为92.37%。可见利用植被指数逐步回归分析和混合像元分解相结合进行植被覆盖度反演能较好的提高模型精度,对植被覆盖度定量估算具有重要的理论意义与实用价值。

表3 模型精度检验结果比较Table 3 Accuracy assessment and comparison of regression models

图6 植被覆盖度实测值与估测值的线性回归模型Fig.6 Predicted values plotted against observations of percentage vegetation cover
5 结论与讨论
本文基于Landsat 8-OLI遥感影像数据,利用逐步回归对研究区所选的16种植被指数进行筛选,建立土地荒漠化(康保县)地区植被覆盖度反演最优估算模型,并结合混合像元分解结果(植被丰度)建立植被覆盖度反演混合模型,通过分析比较和精度评价,得到以下结论:
(1)遥感植被指数(如NDVI等)对荒漠化地区稀疏的植被覆盖反应不敏感,仅用一种或几种植被指数建立植被覆盖度反演模型精度低。在所选16种植被指数中,采用单一植被指数进行荒漠化地区植被覆盖度反演建模,其拟合最高的是归一化植被指数(NDVI)和土壤调节植被指数(SAVI)。利用逐步回归分析筛选出的最优遥感植被指数是土壤调节植被指数(SAVI0.5)、比值植被指数SRN-R和增强型植被指数EVI,所得模型提高了植被覆盖度反演精度。
(2)通过线性混合像元分解建立的植被覆盖度反演模型,所得植被丰度与植被覆盖度的决定系数低于利用植被指数逐步回归反演,但高于单一植被指数与植被覆盖度回归的反演。
(3)混合像元分解和植被指数逐步回归分析综合所建的混合模型的决定系数(R2)和精度都高于植被指数逐步回归反演的植被覆盖度模型的决定系数(R2)和精度,表明植被指数逐步回归与混合像元分解相结合能较好的提高荒漠化地区植被覆盖度反演精度。
本文仅选取了6种遥感植被指数及其衍生植被指数因子进行建模,未对更多的植被指数进行分析研究,并且只与混合像元分解结果建立了混合模型提高了土地荒漠化(康保县)地区植被覆盖度的反演精度,探寻其他更好的植被覆盖度反演因子建模有待进一步研究。
[1]中华人民共和国林业部防治沙漠化办公室.联合国关于在发生严重干旱和/或荒漠化的国家特别是在非洲防治荒漠化的公约[M].北京:中国林业出版社,1994.
[2]高尚玉,张春来,邹学勇,等.京津风沙源治理工程效益[M].北京:科学出版社,2012.
[3]汪晓菲,何 平,康文星.若尔盖县高原草地沙化成因分析[J].中南林业科技大学学报,2015,35(3):100-106.
[4]刘爱霞,王长耀,王 静,等.基于MODIS和NOAA/AVHRR的荒漠化遥感监测方法[J].农业工程学报,2007,23(10):145-150.
[5]郭玉川,何 英,李 霞.基于MODIS的干旱区植被覆盖度反演及植被指数优选[J].国土资源遥感,2011,89(2):115-118.
[6]赵英时.遥感应用分析原理与方法[M].北京:科学出版社,2003.
[7]张 雷,杨 波,程晓凌.干旱区发展的资源环境基础评价:以新疆为例[J].干旱区地理,2011,34(5):713-718.
[8]梁顺林,李小文,王锦地.定量遥感理念与算法[M].北京:科学出版社,2013.
[9]Xiao J F,Moody A. A comparison of methods for estimating fractional vegetation cover within a desert-to-upland transition zone in central New Mexico, USA[J]. Remote Sensing of Environment, 2005, 98(2-3): 237-250.
[10]马超飞,马建文,布和敖斯尔. USLE模型中植被覆盖度因子的遥感数据定量估算[J].水土保持通报,2001,21(4):6-9.
[11]Roberts D A,et al.Mapping chaparral in the Santa Monica Mountains Using Multiple Endmember spectral Mixture Models[J]. Remote Sensing of Environment,1998,65(3):267-279.
[12]John R.Jensen(美).遥感数字影像处理导论[M].陈晓玲,等译.北京:机械工业出版社,2007.
[13]孙 华,鞠洪波,张怀清,等.三种回归分析方法在Hyperion影像LAI反演中的比较[J].生态学报,2012,32(24):7781-7790.
[14]张熙川,赵英时.应用线性光谱混合模型快速评价土地退化的方法研究[J].中国科学院研究生院学报,1999,16(2):169-176.
[15]林 辉,孙 华,熊育久,等.林业遥感[M].北京:中国林业出版社,2011.
[16]李 君,范文义,李明泽.线性混合光谱模型在多光谱遥感影像分类中的应用[J].东北林业大学学报,2008,36(8):45-48.
[17]Lu D,Weng Q. Spectral mixture analysis of the urban landscape in Indianapolis with Landsat ETM+ imagery[J]. Photogrammetric Engineering and Remote Sensing, 2004, 70(9): 1053-1062.
[18]卢 远,林年丰.松嫩平原西部土地退化的遥感动态监测研究——以吉林省通榆县为例[J].地理与地理信息科学,2003,9(2): 24-27.
Modeling percentage vegetation cover of a desert area using Landsat 8-OLI image
MA Zhong-gang1, SUN Hua1, WANG Guang-xing1,2, LIN Hui1, SHE Yu-chen1, ZOU Qi1
(1.Research Center of Forest Remote Sensing & Information Engineering , Central South University of Forestry & Technology,Changsha 410004, Hunan, China; 2. Dept. of Geography, Southern Illinois University, USA)
Percentage vegetation cover is a direct and effective measure used to assess and monitor deserti fi cation. In this study, a novel method that combined stepwise regression and linear spectral unmixing analysis was developed to derive an integrated regression model of percentage vegetation cover against image vegetation indices and vegetation fraction. A total of 134 sample plots were systematically selected in the study area – Kangbao County and percentage vegetation cover data that quanti fi ed deserti fi cation were collected. Landsat 8-OLI image was acquired and a total of 16 vegetation indices were calculated. Linear spectral unmixing analysis was conducted to extract vegetation fraction of mixed pixels that were introduced into stepwise regression. The results were validated using the observations of sample plots and showed that: (1) When individual vegetation indices were used to develop regression models, the vegetation indices that had the highest correlation were normalized difference vegetation index (NDVI) and soil adjusted vegetation index (SAVI). In the case of stepwise regression modeling, soil adjusted vegetation index (SAVI0.5), simple ratio (SRN-R)and enhanced vegetation index (EVI) had signi fi cant contributions and were selected. (2) When only vegetation fraction from linear spectral unmixing analysis was used as an independent variable, the coef fi cient of determination for the obtained model was 0.673,lower than the coef fi cient from stepwise regression, but higher than those when individual vegetation indices were employed. (3) The results of accuracy assessment showed that the stepwise regression based on the vegetation indices led to the coef fi cient of determinationR2and accuracy of 0.719 and 86.70%, and the new method that introduced vegetation fraction together with the vegetation indices as independent variables into the stepwise regression resulted in the coef fi cient of determinationR2and accuracy of 0.807 and 92.37%.This implied that the integration of regression modeling and linear spectral unmixing analysis provided a great potential to increase the accuracy of predicting percentage vegetation cover as a measure of deserti fi cation.
deserti fi cation; percentage vegetation cover; image vegetation index; stepwise regression; linear spectral unmixing analysis
S771.8
A
1673-923X(2016)09-0012-07
10.14067/j.cnki.1673-923x.2016.09.003
2015-05-20
国家林业局荒漠化和沙化监测专题项目“基于遥感影像和少量地面数据的京津风沙源区年度荒漠化趋势监测模型”(20149889);湖南省百人计划特聘教授基金项目(1020990);中国博士后科学基金(2014M562147)
马中刚,硕士生
王广兴,教授,博士
马中刚,孙 华,王广兴,等. 基于Landsat 8-OLI的荒漠化地区植被覆盖度反演模型研究[J].中南林业科技大学学报,2016, 36(9): 12-18.
[本文编校:谢荣秀]
