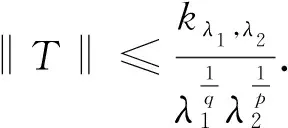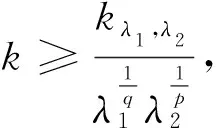On a two-parameter Hilbert-type integral operator and its applications*

SUN Wenbing, LIU Qiong

(Department of Science and Information Science, Shaoyang University,Shaoyang 422000, Hunan, China) (Received 18 March 2016； Revised 11 April 2016)

Abstract In this work, by introducing two parameters λ1 and λ2 and using the method of weight function and the technique of functional analysis, a two-parameter Hilbert-type integral operator is defined and the norm of the operator is given. As applications, a few improved results and some new Hilbert-type integral inequalities with the particular kernels are obtained.

Key words two-parameter Hilbert-type integral operator; norm; weight function; the best constant factor; Hilbert-type integral inequality

(1)

(2)

where the constant factor π/sin(π/p) is the best possible. Inequalities (1) and (2) are important in analysis and its applications[1-2]. Define the Hardy-Hilbert’s integral operatorT:Lp(0,∞)→Lp(0,∞) as follows. Forf∈Lp(0,∞), corresponding to the only

(3)

by (2), we have ‖Tf‖p<π/sin(π/p)‖f‖pand ‖T‖≤π/sin(π/p). Since the constant factor in (2) is the best possible, we find that ‖T‖=π/sin(π/p)[3].

1 Definitions and lemmas

We need the following special functions[10]:

Beta-function

(4)

Γ-function

(5)

Riemann’szeta-function

(6)

and the extendedζ-function

(7)

where Re(s)>1,ais not equal to zero or negative integer. Obviously,ζ(s,1)=ζ(s).

Ifais not equal to zero or negative integer, 0

(8)

Lemma1.1Ifs>0,ais not equal to zero or negative integer, we have the summation formula as

(9)

(10)

assuming thatkλ1,λ2(≥0) is a limited number. Settingu=xλ1yλ2, we have

=kλ1,λ2,(x∈(0,∞)),

(11)

=kλ1,λ2,(y∈(0,∞)),

(12)

(13)

(14)

ProofBy the weighted Holder’s inequality[11]and (12), we find

By Fubini’s theorem[12]and (11), we have

Iλ1,λ2

(15)

By (15) and (13), we obtain (14).

On the contrary, if (14) is true, fory>0, setting the function as

by (14) we obtain

=Iλ1,λ2=Jλ1,λ2

(16)

By (15), we have thatIλ1,λ2<∞. IfIλ1,λ2=0, (13) is tenable naturally. If 0

namely，

So (13) and (14) are equivalent. The lemma is proved.

□

Then we have

(17)

and

(18)

ProofWe easily get

Settingu=xλ1yλ2, by Fubini’s theorem, we have

(19)

(20)

(21)

Putting (20) and (21) into (19), we get (18).

□

2 Main results and applications

Ifθ(x)(>0) is a measurable function,ρ≥1, the function space is set as

(22)

(23)

Hence the equivalent inequalities (13) and (14) may be rewritten in the following abstract forms

(24)

(25)

□

Theorem2.2As Theorem 2.1, inequalities (24) and (25) keep the strict forms, namely,

(26)

(27)

ProofIf inequality (25) keeps the form of an equality, by Lemma1.2 there exist two constantsAandBsuch that they are not all zeroes[11], and they satisfy

□

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

‖f‖p,φ‖g‖q,ψ.

(39)