Riemann面上带cusp奇点的共形度量*
2016-12-19国金宇吴英毅魏志强
国金宇, 吴英毅, 魏志强
(中国科学院大学数学科学学院, 北京 100049)(2016年1月29日收稿; 2016年3月14日收修改稿)
本文主要对Riemann面上带cusp奇点的共形度量进行研究.
1 背景和主要定理
1.1 背景
Calabi在1982年引入extremal Kähler度量[1],目的是在一个紧Kähler流形的固定Kähler类中找到“最佳”的度量.具体地,设M为一个紧Kähler流形,在一个固定的Kähler 类中,extremal Kähler度量是下述Calabi能量的临界点
这里K是Kähler类中度量g的数量曲率.C(g)的Euler-Lagrange方程是
K,αβ=0,1≤α,β≤dimCM,
(1)
这里K,αβ是K的2阶(0,2)型协变导数.因此我们称在一个紧Kähler流形M上满足(1) 的度量为extremal Kähler度量.
Extremal Kähler度量具有较好的性质,比如紧extremal Kähler 流形比一般的Kähler流形具有更好的对称性,而且在光滑的紧Riemann面上,extremal Kähler 度量就是常曲率度量[1].
经典的单值化定理认为,在紧致无边的Riemann面上,对任意的Riemann度量,都会有常曲率度量与之共形等价.单值化定理无疑是经典复分析中非常漂亮和重要的定理.
过去很多人尝试将经典的单值化定理推广到一般的帯边曲面.而过去主要集中在带有奇点的曲面上常曲率度量的存在性问题.
为了推广经典的单值化定理,Chen等[2-3]继承Calabi的思想,研究Calabi能量泛函的变分问题.在这个问题框架内,他们主要研究以下2个方面的问题:
1)任意由有限面积和有限Calabi能量所组成的度量子集的弱紧性问题,引进了cusp奇点,得到有趣的“bubbles on bubbles”现象,并且得到这类度量序列的弱极限如果不为零,则该度量一定有cusp奇点.进而给出cusp奇点的基本性质[2-3].
2)Calabi能量泛函的变分问题.令M为紧Riemann面,g0为M{p1,p2…,pn} 上的Hermitian度量,其中p1,p2…,pn为g0的奇点.如果存在一个光滑函数e2φ,使得在M{p1,p2…,pn}上满足g=e2φg0,此时称g与g0共形等价.记P:={p1,p2…,pn},定义Calabi能量泛函E(g)与面积泛函A(g)分别为:
(2)
其中K为g的Gauss曲率. 定义变分空间G(g0)为
G(g0)={g|g=e2φg0,φ∈H2,2(M),
Calabi能量泛函的变分问题就是要研究在面积泛函固定的情况下,Calabi能量泛函最小,即对于任意g∈G(g0),使得Calabi能量泛函E(g)最小.
我们称Calabi 能量泛函的临界点为extremal Hermitian 度量,它的Euler-Lagrange方程为
ΔgK+K2=C,
(3)
其中K为g的Gauss曲率,C为实常数.式(3)在局部复坐标系(U,z)下等价于
(4)
见文献[4].由(4)可知extremal Hermitian度量有2种特殊情况:
1)K=const,即度量g为常Gauss曲率度量.
2)如果g在局部复坐标系(U,z)下满足
K,zz=0,
(5)
则称g为HCMU(the Hessian of the curvature of the metric is umbilical)度量. 在下文中,假设共形度量g有有限的面积和有限的Calabi能量,即
(6)
Chen[4]进一步研究带有cusp奇点的extremal Hermitian度量的相关性质,并给出Gauss曲率K在cusp奇点附近的相关估计.进而给出带有cusp奇点的extremal Hermitian度量的分类定理.
接着Wang和Zhu[5]将Chen的关于cusp奇点的情况推广到锥奇点情况,他们证明了如果g=e2φ(z)|dz|2为D{0}上面积和Calabi能量都有限的extremal Hermitian度量,则z=0不是cusp奇点就是锥奇点. 进而得到关于锥奇点的分类定理.

本文将就他所提出的问题进行研究,进一步给出当g为HCMU度量时,共形参数在cusp奇点的局部表示.
1.2 本文主要定理
定理1.1 如果g=e2φ(z)|dz|2为D{0}上的共形度量,z=0为g的cusp奇点,如果共形参数φ(z)在cusp点附近有形式:φ(z)=-ln|z|-βln(-ln|z|)+o(ln(-ln|z|)),且余项o(ln(-ln|z|))在z=0附近(包括0点)光滑.

(b) 若g为extremal Hermitian度量,则g在D{0}上面积和Calabi能量有限的充要条件为β=1.

其中,α,β满足下列关系式:
定理1.3 如果g=e2φ(z)|dz|2为D{0}上的共形度量,z=0为g的cusp 奇点,并且在D{0} 上面积和Calabi能量都有限,若g为 HCMU度量,则在z=0 附近共形参数一定可以表示成
φ(z)=-ln|z|-ln(-ln|z|)+lnh(z),
其中,h(z)为在z=0点连续,在0点以外光滑的正函数.
2 预备知识
2.1 弱cusp奇点、cusp奇点、锥奇点


定义2.3 设M是Riemann面,p∈M.(U,z)为p附近的复坐标系且z(p)=0,g为U{p}上的光滑度量.如果g=e2φ|dz|2,并且φ-(α-1)ln|z|(α>0)在p处连续,则称p为g的锥奇点并且g在p处有锥角度2πα.
注记:如果在弱cusp奇点附近满足面积和Calabi能量有限,那么弱cusp奇点就是cusp奇点,见文献[5].
2.2 cusp奇点,extremal Hermitian 度量及HCMU度量的基本性质
设M是一个紧Riemann面,p1,…,pn是M上的n个点,记P:={p1,…,pn}. 设g是MP上的光滑保角度量.设(U,z)为MP上的局部复坐标系,则g在U上可以写成
g=e2φ|dz|2.

在文献[4]中,Chen研究了面积和Calabi能量都有限且只带有cusp奇点的extremal Hermitian度量.一方面,他证明如果该Riemann面为紧致无边的,则extremal Hermitian 度量就是HCMU 度量.另一方面,给出Gauss曲率K在cusp奇点的精确估计,证明了Gauss曲率K在cusp奇点的极限为负常数.

Chen等[7]将文献[6]中的结果推广到既有cusp奇点又有锥奇点的非常曲率HCMU度量上.
3 主要定理与证明
现在返回到我们要研究的问题,在只带有cusp奇点的Riemann面上,共形度量g=e2φ|dz|2满足面积和Calabi能量都有限,则共形参数φ在cusp 点附近有什么样的性质?进一步要问如果度量g为HCMU 度量,那么共形参数在cusp奇点附近又该如何表示?共形参数的余项是否一定光滑?
定理1.1的证明

于是φ(z)变为
φ(z)=-lnr-βln(-lnr)+lnh(z).
(7)
因此g=e2φ|dz|2在DR(0){0}上保持面积和Calabi能量有限等价于
(8)
(9)
其中,K=-e-2φ·Δφ为g的Gauss曲率.
所以由(7)式和(8)式得
由于h(z)在z=0附近有正的上下界,所以
A(g)|DR(0){0}<+∞
等价于
(10)
另一方面由(7)式得
Δφ=-βΔln(-lnr)+Δlnh(z)
(11)
所以由(9)式和(11)式得
2βr(-lnr)2β-2h-2Δlnh+
(Δlnh)2r3(-lnr)2βh-2]drdθ
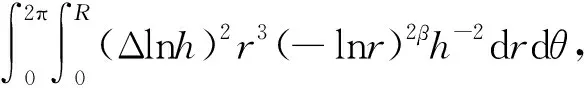
由于h(z)在z=0附近光滑,Δlnh(z)在z=0附近有界,因此后两项绝对可积.于是
E(g)|DR(0){0}<+∞
等价于
(12)

证明(b) 由(7)式和(11)式可知共形度量g的Gauss曲率K为
Δlnh·h-2r2(-lnr)2β,
(13)

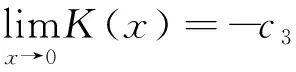

接下来我们将在局部上构造仅带一个cusp奇点的度量,再利用单位分解在S2上构造一个带cusp奇点的度量.

φ(z)=-ln|z|-βln(-ln|z|)-
αln(ln(-ln|z|)).
(14)
我们将证明:g在D{0}上满足面积和Calabi能量有限的充要条件是α和β满足下面条件:
下面给出具体的构造方法.
定理1.2的证明
证明令
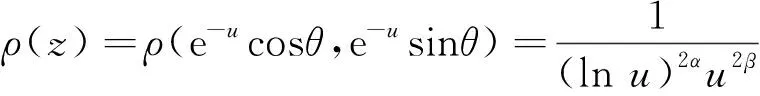
即φ(z)=-lnr-βln(-lnr)-αln(ln(-lnr)),容易验证对于任意的α,β,φ(z)恒满足cusp奇点条件. 再令
ψ(u,θ) =φ(e-ucosθ,e-usinθ)-u
(15)
则面积变为
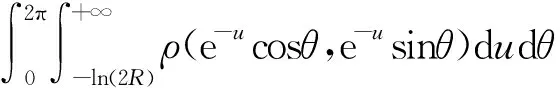

Calabi能量变为
2β(lnu)-4α]2u2β-4(lnu)10αdudθ,
由积分的收敛性可知,
E(g)|D2R(0){0}<+∞
等价于

(16)
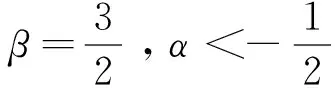
综上若φ有下面形式
φ(z)=-ln|z|-βln(-ln|z|)-
αln(ln(-ln|z|)),
(17)
则g在D2R(0)上满足面积和Calabi能量都有限当且仅当α,β满足下列关系式:
(18)

令p为单位球面S2上的一点,取p点附近的复坐标图(U1,z),使得z(p)=0,z(U1)=D2R(0),其中R为上文提到的.又设
g1=e2φ|dz|2=
(19)

(20)

(21)

由定理1.2的证明并参照定义2.2,可以提出新的cusp奇点的定义,即
定义3.1设M为Riemann面,p∈M,(U,z)为p附近的复坐标图,g=e2φ|dz|2为U{p}上的共形度量, 如果φ在z=0附近有下面形式
φ(z)=-ln|z|-βln(-ln|z|)+lnh(z),
(22)

因此,从定理1.2的证明中可得:即使在面积和Calabi能量都有限的条件下也不能得出cusp奇点与强cusp奇点等价.
下面的定理1.3将要证明:如果度量为HCMU度量并且满足面积和Calabi能量有限,则cusp奇点一定是强cusp奇点,并且此时定义3.1中β=1.
定理1.3的证明


1)存在C′∈,使得在D{0}上有
,
(23)
这里C为(3)式中的常数.由此可得
(24)
2)存在μ<0使得

(25)
并且
(26)

于是可设
(27)
其中λ-1为ω在z=0处的留数,f1为在z=0附近的全纯函数,Φ为z=0附近的全纯函数且Φ(0)=λ-1≠0. 所以由上面的1)、2)、3)并结合文献[7](定理1.1)得到
λ-1dln|z|2+2dRe(f1),
(28)
(29)
由于(28)式左端可分解为
(30)
所以(28)式等价于
d(λ-1ln|z|2+2Re(f1)).
(31)
对(31)式两边同时积分得
=λ-1ln|z|2+2Re(f1)+C,
(32)
其中,C为常数.
由(29)式得
[(K-μ)2(-2μ-K)·

(33)
即
φ(z)=-ln|z|+ln|μ-K|+
(34)
再将(34)式代入cusp奇点条件得
(35)
再对(32)式两边同除ln|z|,利用(35)式得到
(36)
其中,λ-1为ω在z=0(即cusp奇点)处的留数.
由于特征1-形式ω在cusp奇点处留数可正可负,所以Gauss曲率K有2种情况.但无论哪种情况都有下面的式子成立:
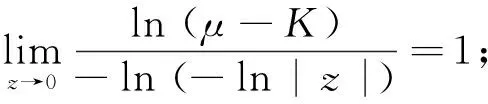
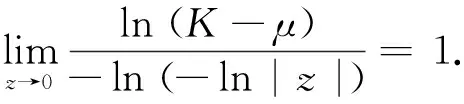
我们证明第1种情况,第2种情况类似.
当K<μ时,由(36)式得
(37)

(38)
由ln的单调性,对(38)式两边同取ln有
(39)
对(39)式两边同除-ln(-ln|z|)有
(40)
由(40)式得到
(41)
所以由(34)式、(41)式共形参数φ(z)在cusp奇点附近一定可以写成

(42)
再由(37)式知道(42)式的余项o(ln(-ln|z|)),在z=0处连续0以外光滑.
所以(42)式经整理得到
φ(z)=-ln|z|-ln(-ln|z|)+lnh1(z),
(43)
其中,h1(z)为在z=0处连续,在z=0以外光滑的正函数.
同理可以求出当μ φ(z)=-ln|z|-ln(-ln|z|)+lnh2(z), (44) 其中,h2(z)为在z=0处连续,在z=0以外光滑的正函数. 所以综上得到如果g为HCMU度量,共形参数在cusp奇点附近一定可以写成 φ(z)=-ln|z|-ln(-ln|z|)+lnh(z), (45) 其中,h(z)为在z=0处连续,在z=0以外光滑的正函数. 推论3.1令M为紧致无边的Riemann面,记P:={p1,p2,…,pn},g=e2φ|dz|2为MP上的extremal Hermitian度量,其中P为M的cusp奇点,且g在MP上保持面积和Calabi能量都有限,则共形参数在cusp 奇点附近一定可以写成 φ(z)=-ln|z|-ln(-ln|z|)+lnh(z), (46) 其中,h(z)为在z=0处连续,在z=0以外光滑的正函数. 证明由文献[4](定理A)我们知道:如果M为紧致无边,g是M{p1,p2,…,pn}上的extremal Hermitian度量,其中p1,p2,…,pn为g的cusp奇点,并且满足面积和Calabi能量都有限,则共形度量g一定为HCMU 度量,进而由上面的定理1.3得到结果. 对于一般Riemann面上的extremal Hermitian度量,其在cusp奇点附近面积和Calabi能量都有限,我们推测共形参数φ在cusp奇点附近也可以表示为 φ(z)=-ln|z|-ln(-ln|z|)+lnh(z), 其中,h(z)为在z=0处连续,在z=0以外光滑的正函数. 因为无论从定理1.3还是最后的推论3.1,都有迹象表明应该会有这样的形式,因此我们会在后续研究中予以讨论.4 后续的讨论
